基于GM（1，Nr）模型的上海生活垃圾可回收量预测研究

都晓艺

摘   要：有效规划垃圾分类容器配置的数量及分布，涉及的一个重要问题是如何准确预测垃圾回收量。基于此，从系统的角度考虑影响生活垃圾可回收量的因素，提出一种改进的GM（1，N）模型—GM（1，Nr）预测模型进行实证分析，并具体从三个方面加以改进，即对原始序列进行转化，结合粒子群算法使其满足建模条件、引入灰色关联分析获得灰色关联序，并通过逐步检验方式确定相关因素个数、通过改进的GM（1，1）模型预测相关因素序列。对上海市可回收垃圾量实例的分析结果表明，与传统的灰色预测模型相比，该模型具有良好的预测性能，未来上海市可回收垃圾量总体上呈现增长趋势，该结果可为上海市政府及相关机构合理规划管理生活垃圾处理工作提供决策依据。

关键词：生活垃圾可回收量；灰色预测模型；GM（1，Nr）；灰色关联分析；粒子群优化算法

中图分类号：X799.3      文献标志码：A      文章编号：1673-291X（2023）09-0049-05

引言

回收站点的规划是保障资源有效回收的重要途径，可回收生活垃圾的预测能为回收站点的规划提供必要依据[1]。对于生活垃圾预测方法，目前的研究主要使用三类方法：多元线性回归方法、智能算法、时间序列分析方法。Araiza等考虑经济和人口变量，采用多元线性回归方法预测城市固体废物的产生率[2]。智能算法对于非线性问题具有良好的适应性，Kannangara等基于决策树及神经网络算法来构建模型，并用于预测加拿大城市固体垃圾的产生量，实验表明，模型表现出良好的预测效力[3]。Navarro等对戈亚斯州一垃圾填埋厂的固体垃圾进行预测分析，考虑季节性的影响，采用SARIMA模型，对居民生活垃圾数据进行拟合预测[4]。Rimaityte等研究发现，时间序列分析针对固体垃圾每周的产生量具有较高预测效力[5]。邓聚龙提出的灰色模型最少只需要4个数据，并且计算较为简单快捷。因此，灰色模型逐渐受到学者的青睐[6]。Hao等利用灰色单变量模型与神经网络结合的方法来预测医疗废物的数量[7]。Chen等提出一种新型的灰色模糊动态模型，预测了台南市的固体垃圾产生量[8]。Ceylan等将传统GM（1，1）模型与ARIMA模型及AVR进行了对比研究[9]。Intharathirat等通过将灰色模型与卷积积分相结合，预测泰国城市固体垃圾[10]。Kazancoglu等基于GM（1，1）模型估计了新型经济体的电子废物数量[11]。针对灰色多变量模型，缺乏在生活垃圾相关的应用研究，主题主要在社会、经济、环境、能源、工业、农业等领域。Pai等利用GM（1，N）模型研究环境影响评估的相关因素，并对环境影响进行预测[12]。

本文通过引入两个常数来满足基本的建模条件，并结合粒子群算法找寻最优的值。其次针对一些不必要影响因素的存在可能也会导致模型的预测准确性不高，本文通过灰色关联分析确定灰色关联序，并结合逐步检验显著变量的方式寻求最佳N。最后对传统的GM（1，N）做预测时，需要GM（1，1）的预测，而GM（1，1）本身的缺陷可能导致较大的预测误差，因此本文通过利用初始值改进的GM（1，1）来提高传统GM（1，N）的模拟精度，从而对GM（1，N）模型进行改进。

一、方法

（一）GM（1，Nr）模型的构建

本文将从三个方面，对传统的GM（1，N）模型进行改进，分别是对原始序列进行转化结合粒子群算法使其满足建模条件、引入灰色关联分析获得灰关联序并通过逐步检验方式确定变量个数、通过改进的GM（1，1）模型预测相关因素序列。我们将改进的GM（1，N）模型命名为GM（1，Nr），GM（1，Nr）模型预测一个系统的程序步骤如图1。

定义1 设序列Xi（0）=（xi（0）（1），xi（0）（2），...xi（0）（n）），i=1，2，...，Nr，其中，X1（0）为系统特征数据序列，X2（0），X3（0），...，XN■为相关因素序列，序列Xi（1）为Xi（0）的1-AGO序列，Z1（1）为Xi（1）的紧邻均值生成序列，称X1（0）（k）+■bixi（1）（k）为GM（1，Nr）模型，并称■+az1（1）=■bixi（1）（t），为GM（1，Nr）模型的白化方程。

传统灰色多变量模型要求序列满足非负条件以及准光滑性的条件[13]，因此不满足条件的数据序列无法建立灰色模型，本文通过引入两个常数对原始序列的初始状态进行变换，以扩展灰色模型的适用性。

定理1：设原始序列的初始状态为Xiraw（0），其中i=1，时，为系统特征数据序列，i>1时，为相关因素序列，则变换后的原始序列为Xi（0）：

Xi（0）=（xi（0）（1），xi（0）（2），...xi（0）（n））≥0，n≥4（1）

Xi（0）=Xiraw（0）+C1+C2，i=1，2，...，Nr

其中，C1，C2分别为第一、第二非负综合加和因子，分别满足以下条件：

C1=                      0  if：？坌k∈（1，2...，n），xiraw（k）≥0max|xiraw（k）|  if：？埚k∈（1，2...，n），xiraw（k）<0，i=1，2，...，Nr

（2）

C2=0   if：满足准光滑性条件C2≥0C2≥max■ if：不满   （3）足准光滑性条件，i=1，2，...，Nr

定理2：對于任意数据序列，始终存在两个非负常数C1和C2，序列的元素加上这两个值即可满足灰色模型建模的两个条件，即满足非负条件及准光滑性条件[14]。

尽管我们可以通过式（3）得到C2的必要条件，但不同的值会带来不同的预测误差。因此，为了最小化预测误差，我们采用非线性规划的方式确定C2的值。

以建模平均误差最小化为目标，将模型参数、时间响应式等已知条件作为约束条件，构建非线性优化模型，求解C2的最优值：

min avg（e（k））=■■■，i=1，2，...，Nr

s.t.x1（0）（k）=-az1（1）（k）+■bi（xi（1）（k））                 式（2）                 式（3）（4）

本文采用粒子群智能优化算法对该非线性优化模型进行求解，从而解得C2的最优值。

现有研究一般运用灰色关联分析方法进行模型的相关因素变量个数的确定，但其缺陷在于影响因素的纳入也可能导致模型精度的降低。因此，本文采用灰色关联度与拟合预测的结果相结合的方式，确定最优的相关变量的个数，设为Nr。

具体而言，首先，通过序列的灰色关联分析，得到系统特征数据序列与相关因素序列之间的灰色关联度。其次，进行逐步检验。根据关联度排序，按由高到低的顺序，每次选择1，2，…，N个相关因素序列来建立模型，计算相应的模拟及预测误差。最后选取表现最优的GM（1，N）所对应的相关变量，此时的N即为Nr。

定理3：设系统特征数据序列为X（0）（t），X（i）（t）（i=1，2，...，N）为相关因素序列，则系统特征数据序列与相关因素序列之间的关联度为[6]：

R=■■ξi（t）（5）

其中，ξi（t）=■，为灰色关联系数，0<ρ<1，ρ一般取0.5。

定理4：设Xi（0），Xi（1）（i=2，3，...，N），Z1（1）如前所述，矩阵B、YN■以及参数列矩阵分别为：

B=-z1（1）（2）   x2（1）（2）  ...  xN■（1）（2） -z1（1）（3）   x2（1）（3）  ...  xN■（1）（3）...                     ...-z1（1）（n）   x2（1）（n）  ...  xN■（1）（n），YN■=x1（0）（2）x1（0）（3）...x1（0）（n），PN■=ab2...bN■

估计模型参数如下：

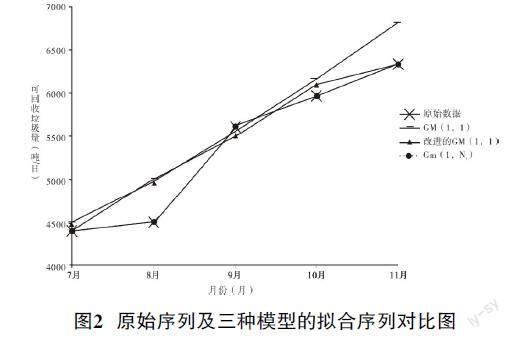
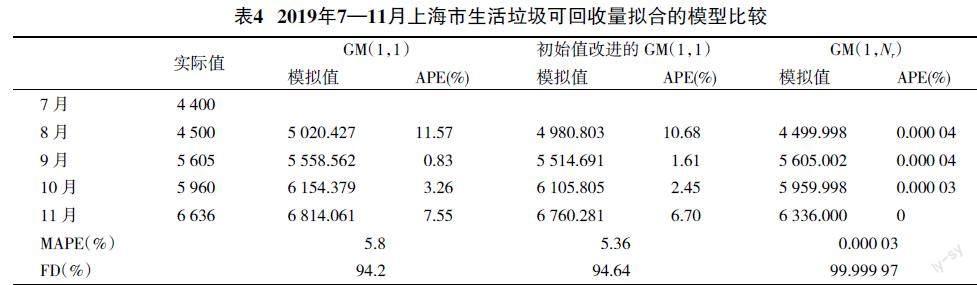
PN■=B-1YN■，|B|≠0  if n=Nr+1PN■=（BT）-1BTYN■  if n>Nr+1PN■=BT（BBT）-1YN■，  if n

定理5：设B、YN■与PN■为前述条件，X2（0），X3（0），...，XN（0）的预测值由初始值改进的GM（1，1）模型得到[15]，则x1（0）（k），k=2，3，...，n的拟合及预测值为：

x1（0）（k）=ax1（0）（k-1）+β2x2（1）（k）+...βN■xN■（1）（k），k=2，3，...，n（7）

其中，βi=■，a=■

（二）模型精度衡量

我们利用三个评估方法来衡量该模型的预测效果，分别为绝对百分比误差（APE）、平均绝对百分比误差（MAPE）以及拟合度（FD），表示如下：

APE=■×100%（8）

MAPE=■■■×100%（9）

FD=1-MAPE（10）

二、实证分析

（一）上海市生活垃圾可回收量概况

当前我国尚未建立起高效的回收网络，与回收网络密切相关的是垃圾分类政策措施，而我国垃圾分类起步较晚，2019年7月，上海才正式成为我国首个垃圾分类城市。在此档口下，对试点城市回收垃圾进行预测，不仅能有效衡量试点城市的垃圾回收的效果，而且能为政府部门制定今后的垃圾管理相关政策提供决策依据，因此有必要对上海市生活垃圾的可回收量进行预测。

经济、人口、社会因素都能促使上海市的可回收生活垃圾产生量快速上升。GDP、城镇居民人均生活消费支出、城市人口密度等诸多因素都对可回收生活垃圾的产生量具有一定影响[10]。由于相关数据来源较为有限，故本文纳入考虑的因素为商品零售总额、国际旅游入境人数、上海生产总值、人均可支配收入，并作为模型的相关因素变量。而上海市生活垃圾可回收量作为系统特征行为变量。表1具体列出了2019年7—11月的上海市生活垃圾可回收量及主要影响因素统计资料，其中上海市生活垃圾可回收量来自上海市绿化和市容管理局，主要影响因素数据均来自上海市统计局。由于商品零售总额、上海生产总值、人均可支配收入只有季度数据，本文首先进行了数据预处理，利用eviews软件中的Quadratic-match sum方法将季度数据转化为月度数据，从而得到表1。

（二）识别相关因素变量个数

首先判断实验数据是否满足非负条件及准光滑性条件，结果显示，数据通过非负及准光滑性检验，可以进行后续灰色模型的建立。通过灰色关联分析得到影响上海可回收生活垃圾产生量因素与其的灰色关联度，并进行排序获得灰色关联序，可得出结果如表2。

由结果可知，所有因素与可回收生活垃圾的产生量的灰色关联度均大于0.5，因此，上海生产总值、国际旅游入境人数、人均可支配收入与商品销售总额都将对上海可回收生活垃圾量造成显著影响。进一步，逐步选取显著变量序列来建立灰色模型，通過拟合效果的检验来确定，以建立最终的GM（1，Nr）模型。经检验可得表3，综合拟合误差与预测误差，选取前三个变量均为最优情况，因此去掉商品销售总额变量，确定模型变量个数为3个，最终的参数为4。

（三）预测分析

本文实验在MATLAB R2017b上进行，接下来建立改进的GM（1，Nr）模型，由于上海市市容管理局公布的数据有限，仅含2019年7—11月、2020年3月、5月及6月的数据，故本文对2019年7—11月的上海市生活垃圾可回收量进行模型拟合，对2019年12月至2020年6月的数据进行模型的预测并进行部分检验。本文同时建立传统的GM（1，1）模型与初始值改进后的GM（1，1）模型[15]进行对比分析。

GM（1，Nr）与另外两种灰色模型结果的对比见下页表4。根据表5的MAPE预测精度标准，传统GM（1，1）模型，基于初始值改进的GM（1，1）以及GM（1，Nr）的拟合结果均较小，均在10%以下，说明灰色模型对小样本数据具有较好的拟合性能。但是GM（1，Nr）的MAPE值最低，显著优于其他两个灰色模型。对于FD值，GM（1，Nr）为99.999997%，接近100%，而传统GM（1，1）和基于初始值改进的GM（1，1）的值分别为94.2%和94.64%。以上结果表明，与单变量灰色预测模型相比，GM（1，Nr）具有更高的拟合精度。

同时，我们可以看到，基于初始值改进的GM（1，1）的MAPE值低于传统GM（1，1）模型，这表明新数据的纳入将提高预测精度，与以前的研究结论一致。根据图2，很明显可以看到，GM（1，Nr）模型的拟合曲线与实际值曲线最接近，且趋势与实际曲线相似，因此具有最佳拟合效果。而对于其他两个灰色单变量模型，虽然其拟合曲线与实际值曲线之间总体上呈现同步趋势，但是有较大的波动，意味着有较大的误差。

以上分析说明GM（1，Nr）模型对上海生活垃圾可回收量的适应性最佳，基于此，本文采用基于GM（1，Nr）模型的预测。首先对2019年12月至2020年6月的数据进行预测，得到预测精度，再据此对2020年7月至2021年10月进行预测。

本文预测时，结合初始值优化的GM（1，1）模型，预测相关因素序列及系统特征数据序列，得到2019年12月至2020年6月的上海市生活垃圾可回收量预测结果，见表6。

接下来进行模型预测精度的衡量。根据2020年上海市绿化与市容管理局最新发布的仅3个上海市可回收生活垃圾量的数据，分别是2020年3月，2020年5月，2020年6月。由于2020年3月疫情较为严重，对模型的影响较大，属于异常值，故剔除。2020年5月，2020年6月的疫情好转，对模型的影响较小，因此保留。对2020年5月，2020年6月计算相应的预测误差，数据见表7，平均绝对误差百分比为5.49%，模型预测精度优秀。

从表6，可以看出上海市可回收生活垃圾量在2019年12月呈现增长趋势，为6 405.47吨/每日，但2020年1—6月，数据出现轻微的下降，这可能是由于某些外在随机因素的影响，例如疫情的影响，导致可回收垃圾量从2020年1月开始趋于下降，但依然稳定在6 100吨/每日以上，并且随着疫情的好转，影响逐渐减小，可以预见可回收垃圾量将继续上升。

基于此，对2020年7月到2021年10月的数据进行预测，得到具体数值如表8。分析可知，从整体上看，上海市可回收垃圾量呈现增长趋势，预计未来依然能保持增长态势。

三、结论

本文通过结合粒子群算法、灰色关联分析方法及初始值改进的GM（1，1）模型，构建灰色预测GM（1，Nr）模型，并与传统的GM（1，1）及初始值改进后的GM（1，1）进行对比，可得如下结论：第一，总体而言，本文所提出GM（1，Nr）模型相比其他模型产生量有更好的效果，表明该模型是预测上海市可回收生活垃圾量的有效方法。將新模型应用至上海市生活垃圾可回收量的预测案例，并与传统GM（1，1）模型及初始值改进后的GM（1，1）进行的对比结果表明，GM（1，Nr）模型的拟合精度显著高于其他两个模型，所提出的模型可为其他城市的可回收生活垃圾量的预测与管理问题提供决策依据。第二，运用灰色关联分析法，可得出商品零售总额、国际旅游入境人数、上海生产总值、人均可支配收入几个影响因素，均对上海可回收垃圾产生量有显著影响。因此，上海市可回收生活垃圾量的产生归因于上海市经济发展水平，国际化程度以及居民生活水平，这一结论与其他研究不谋而合。第三，基于GM（1，Nr）模型进行预测，得到上海市接下来数月的可回收垃圾量，结果表明未来上海市可回收生活垃圾产生量将持续增长下去，可为上海市有效地组织规划生活垃圾处理工作提供一定的参考依据，例如可回收垃圾回收站的数量分布。因此，本文所提出的GM（1，Nr）模型是分析和预测上海市可回收生活垃圾产生量的有效工具，但同时也应注意，本文的研究具有一定的局限性。例如在影响因素的选取中，没有考虑定性的因素。最后，若需要更为准确地预测未来的数据，需要重新建立模型，带入最新的数据。

参考文献：

[1]   彭茂.再生资源回收物流发展影响因素的DEMAEL分析[J].软科学，2016，30（6）：140-144.

[2]   Araiza A.J.， Rojas V.M.， Agular V.R. Forecast generation model of municipal solid waste using multiple linear regression[J].Global Journal of Environmental Science and Management，2020，6（1）：1-14.

[3]   Kannangara M.，Dua R.，Ahmadi L，et al.Modeling and prediction of regional municipal solid waste generation and diversion in Canada using machine learning approaches[J].Waste Management，2018，74（3）：3-15.

[4]   Navarro J.，Diamadopoulos E.，Ginestar D.Time series analysis and forecasting techniques for municipal solid waste management[J].Resources Conservation and Recycling，2002，35（3）：201-214.

[5]   Rimaityte I.，Ruzgas T.，Denafas G，et al.Application and evaluation of forecasting methods for municipal solid waste generation in an eastern-European city[J].Waste Management & Research，2012，30（1）：89-98.

[6]   邓聚龙.灰理论基础[M].武汉：华中科技大学出版社，2002：210-233.

[7]   Hao H.，Zhang J.，Zhang Q.，et al. Improved gray neural network model for healthcare waste recycling forecasting[J].Journal of Combinatorial Optimization，2019，42（4）：813-830.

[8]   Chen H. W.，Chang N.B. Prediction analysis of solid waste generation based on grey fuzzy dynamic modeling[J].Resources，conservation and Recycling，2000，29（1）：1-18.

[9]   Ceylan Z.，Bulkan S.，Elevli S. Prediction of medical waste generation using SVR，GM（1，1） and ARIMA models：a case study for megacity Istanbul[J].Journal of Environmental Health Science and Engineering，2020，18（2）：687-697.

[10]   Intharathirat R，Salam P A，Kumar S，et al.Forecasting of municipal solid waste quantity in a developing country using multivariate grey models[J].Waste Management，2015，39（3）： 3-14.

[11]   Kazancoglu Y.，Ozbiltekin M.，Ozen Y.D.O.，et al.A proposed sustainable and digital collection and classification center model to manage e-waste in emerging economies[J].Journal of Enterprise Information Management，2020，34（1）：267-291.

[12]   Pai T.，Chiou R.，Wen H.Evaluating impact level of different factors in environmental impact assessment for incinerator plants using GM（1，N） model[J].Waste Management， 2008， 28（10）：1915-1922.

[13]   劉思峰，郭天榜，党耀国.灰色系统理论及其应用[M].北京：科学出版社，2010.

[14]   Guo H.， Xiao X.， Forrest T.J. A research on a comprehensive adaptive grey prediction model CAGM（1，N）[J].Applied Mathematics and

Computation，2013（225）：216-227.

[15]   党耀国，刘思峰，刘斌.以x^（1）（n）为初始条件的GM模型[J].中国管理科学，2005，13（1）：132-135.

[16]   Hu Y.C. Electricity consumption prediction using a neural-network-based grey forecasting approach[J].Journal of the Operational Research

Society，2017，68（10）：1259-1264.

[责任编辑   文   欣]