井下核磁共振测井数据压缩的实现
张 岩, 于海龙
(中国石油大学(北京)地球物理学院,北京 102249)
由于岩石骨架的弛豫时间很短,核磁共振测井对岩石骨架的变化不敏感,可以相对精准地测量地层的渗透率、饱和度等信息,并在评价复杂特殊岩性,识别非常规油气藏等方面也有着十分重要的应用[2]。目前,电缆核磁共振测井仪器广泛应用于各大油田测井作业中,但由于钻井液侵入等因素的影响,对储层信息的精确评价面临挑战[3]。面对以上的问题,随钻核磁共振测井技术应运而生。这种测量技术是在仪器钻井的同时进行储层流体的测量,也就是在钻井液侵入前或很浅时就已经完成了探测,很好地解决了电缆核磁测井的不足之处[4]。随钻核磁共振测井不仅能够准确地识别流体类型和计算储层的孔隙度,还能够应用在水平井和斜度较大的井中,根据测得的参数及时改变井眼轨迹,从而最大限度地增加产能[5]。对于随钻测量而言,井下数据的实时传输至关重要,而钻井液脉冲是常用的传输方式[6]。但是由于随钻测量仪器的传感器不断升级,随钻测量系统需要传至地面的数据量大幅提升[7]。目前已知的最快传输速率仅为50 bit/s,无法满足测井数据实时传输的需求。因此数据在井下的处理、压缩就十分必要。压缩后的数据能按照钻井液脉冲规定的速率实时传输到地面,然后解压缩并显示最终结果[8]。国外对于测井数据压缩的研究比较早,Gardner等[9]把变长编码技术应用于测井数据压缩并取得了较为理想的压缩比,这种编码算法的压缩比因为测井数据类型变化而增大或降低,范围在1.2∶1到22∶1的区间,但是算法本身比较繁琐,运算的时间也比较长。斯伦贝谢公司将图像数据压缩技术应用到了井下井眼成像数据,在数据不失真的情况下压缩比达到了50,较好地解决了带宽不足引起的数据传输问题[10]。中国学者也对此进行了深入研究。在声波测井领域,将一维的声波数据经过数据重组后转化为二维声波图像,经过正交变换后将得到的小波系数按类划分,分别采用不同的压缩方法联合进行编码压缩[11]。在超声电视测井图像压缩方面,由于图像会携带大量数据信息,因此对图像进行分块处理,将分成的若干个子块进行离散余弦变换后,进行量化处理,然后采用LZW算法进行编码[12]。但以上研究并没有综合全面考虑到仪器在井下特定环境下的计算能力和功耗导致数据难以实时上传的问题。目前中国的随钻测井技术还不是很成熟,研究更多的还是如何从提高带宽的角度来增加传输速率,例如对传输方式进行建模分析,对脉冲信号进行检测和对信号特征进行提取,对测井数据本身压缩的维度进行研究相对较少。笔者针对由于井下传输速率较慢导致核磁共振测井数据实时上传较难的问题,根据井下仪器的特点,设计适用于FPGA(现场可编程门阵列)实现的压缩解压缩算法。
1 数据压缩原理
本文中所采用的数据压缩解压缩算法的整体流程如图1所示。首先把输入的数据进行预处理,按照8×8数据块的形式输出,然后把得到的系数矩阵进行离散余弦变换(DCT);为了有效地提高压缩比,下一步进行均匀量化,此步骤相当于进行有损压缩,量化系数决定了最终的压缩比和失真程度[17-18];然后通过本文规定的数据扫描方法将数据输出,对输出的数据采用熵编码的方式得到AC和DC码流,最终整合后输出。数据解压缩算法可以理解为数据压缩算法的逆过程,按照相应的进行逆变换即可[19-21]。

图1 数据压缩解压缩算法流程Fig.1 Flow chart of data compression and decompression algorithm
1.1 数据预处理
基于DCT变换的联合熵编码算法在图像数据压缩处理中常常被用到[13],由于图像数据包含的信息比较多,因此对于图像数据要求对数据中的所有的点进行压缩[14-16];但是二维核磁数据与图像数据不同之处在于,二维核磁数据并不是一幅图中每一个点都包含有效的信息,二维核磁数据谱图如图2所示。由图2可知,数据中包含有效信息以外的部分,有很多空白的区域,这些空白的区域是一些随机的噪声数据或者误差数据。在设定一个阈值后,这些空白区域的值即为0,由此可知二维核磁谱中包含了大量的零值。所以数据在进行量化之前,可以对核磁数据进行预处理。

图2 二维核磁数据谱Fig.2 Two-dimensional NMR data spectrum
由于本文中数据压缩是分成多个8×8子块进行输入的,因此在数据输入时,检测系统检测输入的每个8×8子块数据是否全为0,若全为0,则直接编码为0000;只要输入的子块数据中存在不为零的情况,则按照正常设计的数据压缩编码方式进行编码。最后把两部分整合进行输出。由此针对核磁反演后数据组成二维谱数据的特点,采用以上的预处理方法大大减少了所需要进行联合熵编码的数据量,进而有效提高了系统的压缩比和压缩效率。
1.2 离散余弦变换和反变换
DCT变换的基本单元是数据块,所以采样数据即是把输入数据按固定尺寸切割成若干个8×8块矩阵,然后对每一个矩阵分别进行二维的DCT变换,得到的系数中第一个系数称为AC系数,其他63个系数称为DC系数,这里规定AC系数附近的区域称为高频区域,远离AC系数的区域称为低频区域,具体来说变换后左上角的8个数据为高频系数,余下的系数叫做低频系数[13-14]。
1.3 量 化
每个块数据经过DCT变换后,然后进行量化和扫描才能进入编码阶段。量化即将离散余弦变换后输出的每个块数据,除以相同的数值,数值的大小从某种程度上来说直接决定了此压缩算法的压缩比和数据压缩解压缩后的失真情况,数据块点除的数值越大,那么压缩比就越高,但是同时失真情况也就越明显。
1.4 扫描变换
经过之前的量化,得到的系数矩阵的左上方高频分量区域存在一些非零值,其他绝大多数低频分量区域都是零值或者是近似于零的数值。由于在FPGA嵌入式开发硬件中的存储单元都是以线性单元进行存储的,所以无法按照以上的矩阵形式直接输入到存储器中。若直接按照矩阵排列的形式从上到下的顺序对外输出,那么在存储器中的序列连续零值的数量将会明显受到影响。为了解决上述难题,采用了按照“之”字形的顺序对数据进行扫描输出,这里也可以称其为Zig-Zag扫描,具体的扫描输出方式如图3所示。经过Zig-Zag方式的扫描后,为后续的熵编码打下了夯实的基础。
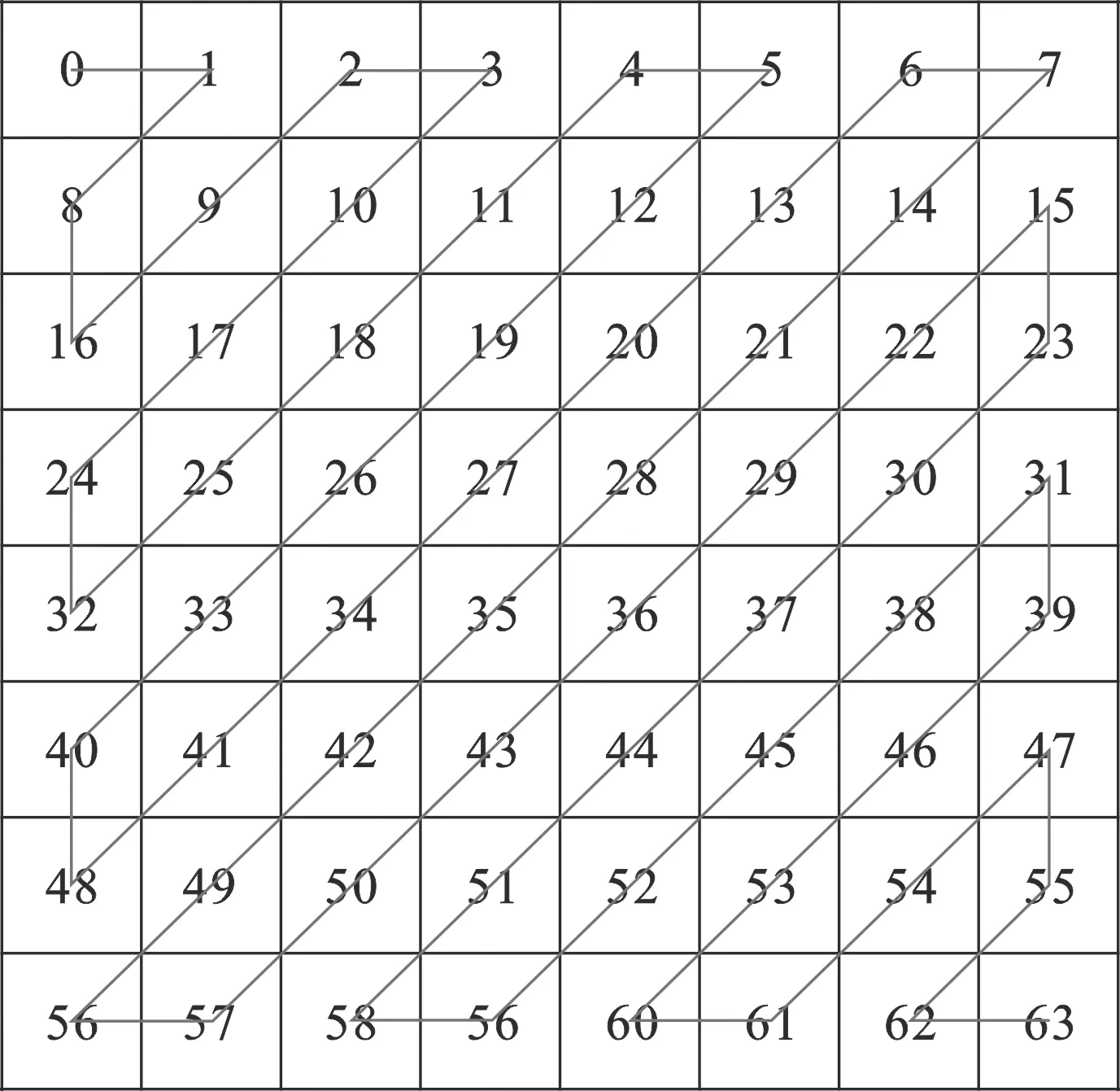
图3 Zig-Zag扫描方式示意图Fig.3 Schematic diagram of Zig-Zag scanning mode
1.5 熵编码
经过上述的一系列操作后,数据之间的相关性被极大程度地降低了,经过量化后数据块中的AC系数相对比较大,但是由于相邻的数据块之间的直流分量的相关性比较强,因此数据块前后的DC差值就会相对比较小,因此采用差分编码(DPCM)的方式对其进行编码。由于之前的系数已经过量化操作,并且按照规定的顺序对数据进行输出,因此量化后的AC系数会有大量连续的零值。针对这种形式可以采用游程编码(RLE)的方式对其进行编码,在一定程度上也减少了数据量。最后进行霍夫曼编码,编码方式为首先将上述得到的系数转换成中间形式,然后通过查找霍夫曼码表上所对应的值进行相应的编码,最后两部分整合将码流输出。
2 压缩与解压缩算法的设计
2.1 压缩模块设计
经过编译综合后得到二维DCT模块程序综合RTL框图如图4所示。NMR_DATA模块产生仿真验证二维DCT变换模块所用到的数据;在DCT1模块中实时地进行串并转换,一维离散余弦变换和并串转换;经过上述的计算后,输入到RAM_CTRL存储管理器中进行缓存和转置操作;得到的数据传输给DCT2模块,经过RAM_CTRAl模块处理的数据经过此模块时再进行一次一维离散余弦变换计算,在使能信号为高电平的条件下经过dout端口输出最终变换得到的结果。

图4 2D-DCT模块程序综合RTL框图Fig.4 RTL block diagram of 2D-DCT module program synthesis
FPGA扫描模块程序综合RTL框图如图5所示,图中ROM_DATA模块产生ROM_SAOMIAO模块的读地址dct_out,ROM_SAOMIAO模块内置初始化Zig-Zag扫描顺序数据矩阵,当读地址address被赋值为ROM_DATA模块的输出dct_out时,ROM_SAOMIAO模块开始按照Zig-Zag扫描顺序进行扫描,处理完成后将数据送入RAM中进行输出。
由于在进行熵码时对DC系数和AC系数这两种系数所采用的编码方式是不一样的,因此需要在进行霍夫曼编码前进行分割处理,其分割提取模块程序综合RTL框图如图6所示。DATA_SEP模块对从ZIG_ZAG模块中流出的数据进行处理,由端口data输入,每次输入的64个数据处理器会把输入的第一个数值当做DC系数,之后的63个数值当做AC数据,分别在ac_en和dc_en都使能的条件下,由ac_data和dc_data两个端口分别输出数据。
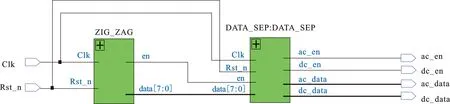
图6 DC、AC系数分割提取模块程序综合RTL框图Fig.6 DC, AC coefficient segmentation module program synthesis RTL block diagram
2.2 解压缩模块设计
数据解压缩的设计采用了类似于数据压缩模块的方法,只是对每个模块进行相逆的数据变换和计算,首先对压缩后的码流进行熵解码,解码后的数据通过反扫描变换和反量化得到的重构系数进行二维的反离散余弦变换后输出,得到的结果即为解压缩数据。由于数据压缩和解压缩两个模块的设计思路相似,所以本部分从设计实现电路的结构框图的角度对数据解压缩系统进行简要的说明。
熵解码模块的详细设计实现主要由两个模块构成,分别是DC解码模块和AC解码模块。对于压缩后得到的二进制码流,在硬件的内部要判断是属于DC系数还是AC系数,从而按照不同的方法对其进行解码,解码后的数据并不是真实值,而是“解码的中间格式”,这一点与编码时相类似。因此要将得到的结果暂存在FIFO中,按照时钟设计的要求,再把存在FIFO中的码流取出进行二次解码,然后将得到的结果整合输出。
反量化反Zig-Zag模块的实现由一个量化表、一个存储反扫描顺序地址的ROM、一个二选一多路器、一个乘法器、一个控制模块和两块RAM构成的乒乓存储器所组成。
二维反离散余弦变换的实现过程类似于之前使用的行列分解法,首先对输入的矩阵数据进行一维反离散余弦变换,得到的数据存储在转置寄存器中进行矩阵行和列的互换,然后对其转置操作后的矩阵按照列的顺序再进行一次反离散余弦变换,得到的结果即为最终的解压缩数据。
3 压缩算法的硬件测试与分析
图7为数据压缩解压缩算法验证平台,主要由开发板和上位机两部分组成。测试过程如下:首先把待测试的数据由上位机通过串口发送给开发板,经过FPGA的压缩解压缩处理后,把得到的数据再上传给上位机,并通过上位机中的调试助手进行显示,在各个模块验证阶段,将处理后的数据与理论值进行对比验证压缩各个模块设计的正确性,进而从量化的角度得出设计正确的结论;然后再利用模拟的二维核磁数据和真实的二维核磁数据验证阶段,将二维数据在不同压缩比下经过压缩解压缩处理后得到的数据所对应的二维谱,与原始数据所对应的二维谱进行对比,进而验证本文设计的压缩解压缩算法整体的正确性。

图7 硬件验证平台实物Fig.7 Physical map of hardware verification platform
3.1 压缩算法各模块的硬件测试与分析
根据测试的要求,利用主控的FPGA来产生满足测试条件的时序和数据源,将需要利用的数据存放在其内置的ROM中,根据时序条件有序地对待测试的数据进行输出,之后经过待测试模块的运算后,将结果传输给上位机的调试助手进行显示,再将其得到的结果和理论运算结果相对比,进而来验证每个模块硬件算法设计的正确性。
在一维离散余弦变换模块,输入从128到65依次递减的共64个整数值进行验证,图8(a)为该数据经过变换后的理论结果,图8(b)为基于设计的硬件算法变换后得到的结果。对比后发现,硬件算法得到的结果和理论结果相一致,说明了一维离散余弦变换硬件算法设计的正确性。由于上位机调试助手显示的数值只能用Hex或ASCII表示,所以此处和下文测试得到的结果都用十六进制数的方式来表示。其他模块的测试方法和此处相同,得到的测试结果和理论值一致,说明其他各个模块设计的正确,此处就不一一赘述。
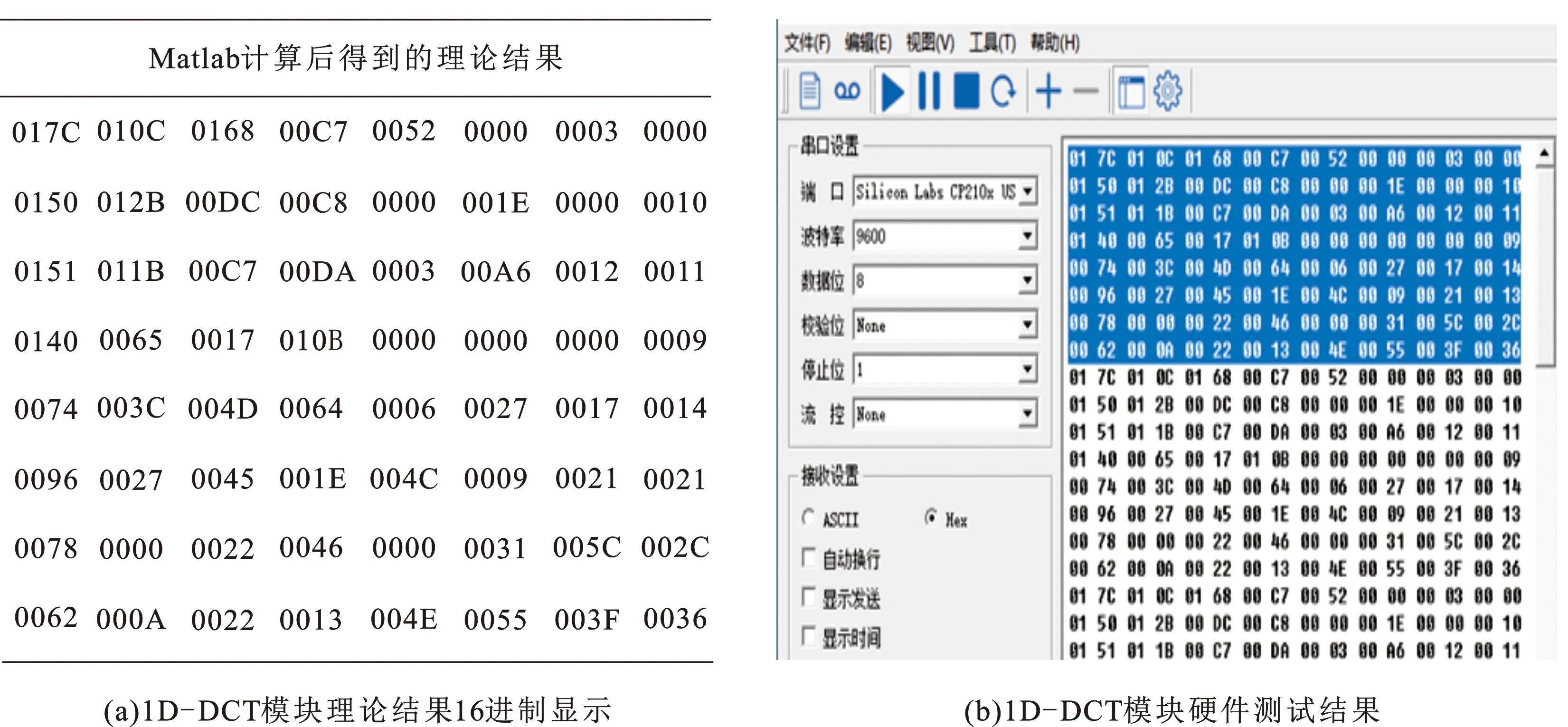
图8 1D-DCT模块理论结果及其硬件测试结果Fig.8 Theoretical results and hardware test results of 1D-DCT module
压缩比和量化系数相关,这里也是通过改变量化系数进而改变数据的压缩比;为了更加有效验证数据压缩解压缩算法的压缩性和有效性,分别采用模拟的二维核磁共振测井数据和真实的二维核磁共振测井数据进行验证。
3.2 模拟D-T2谱数据在不同压缩比下的对比
构建的模拟二维核磁共振D-T2数据谱如图9所示,该数据谱中的3个区域由左到右分别为构建的束缚水模型、可动水模型和轻质油模型。该模型中的3种流体组分都服从高斯分布,流体的总孔隙度为30%,其中束缚水流体的孔隙度是8.5%,可动水流体的孔隙度是9.5%,轻质油的孔隙度是12%。在该模型中,扩散系数D的布点范围是1×10-7~1×10-3cm2/s,纵向弛豫时间T2的布点范围是1~1×104ms。布点方式按照对数等间隔布点,D和T2的布点个数都为32。其中束缚水的D和T2分别为2.5×10-5cm2/s和20 ms,可动水的D和T2分别为2.5×10-5cm2/s和200 ms,轻质油的D和T2分别为1.5×10-6cm2/s和500 ms。
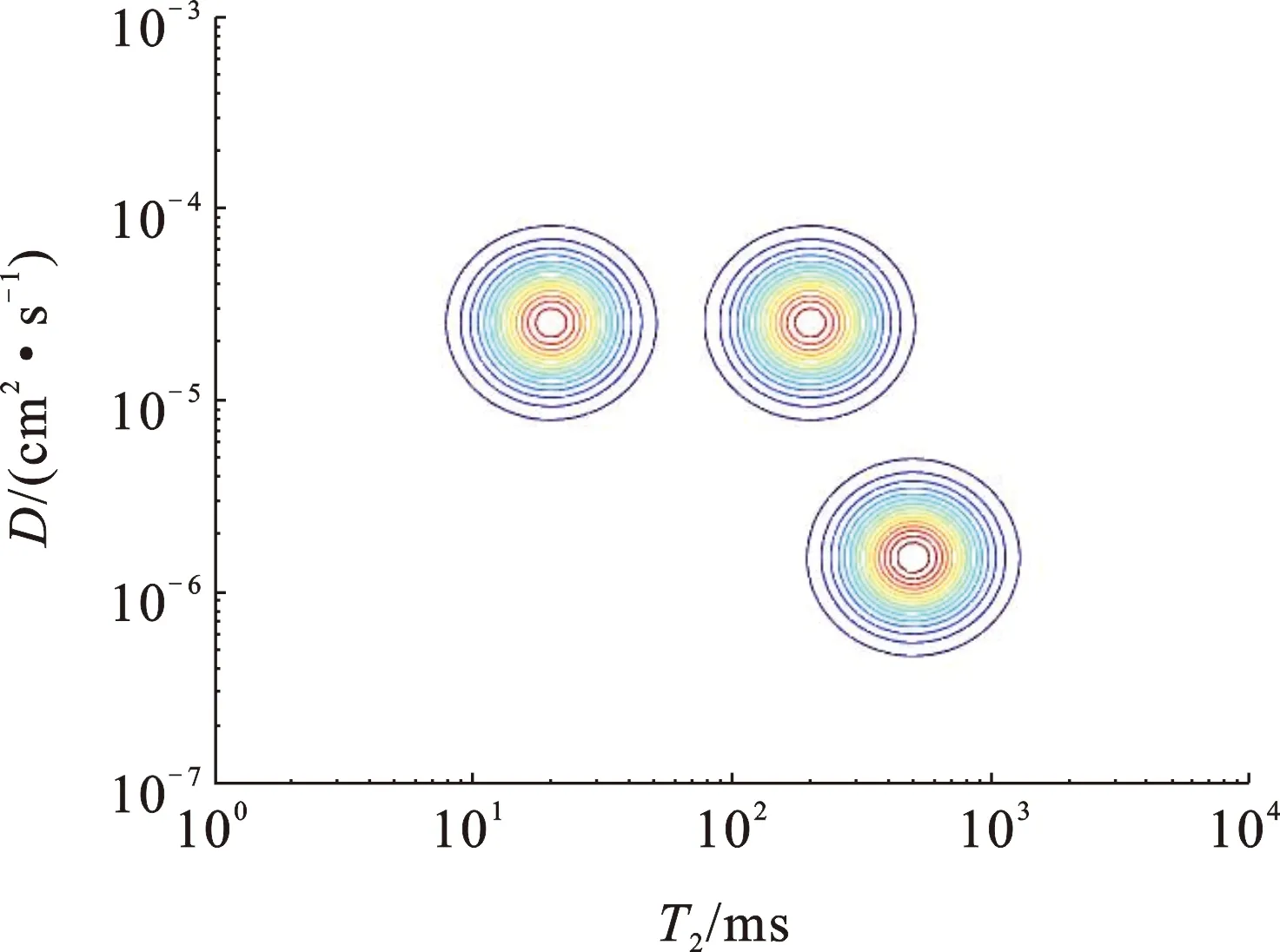
图9 原始模拟D-T2谱数据Fig.9 Raw simulated D-T2spectral
图10为不同压缩比(r)下原始的二维D-T2谱数据经过压缩解压缩后的失真情况。由图10可知,当压缩比小于44时,可以保证原始数据在压缩解压缩后,数据的失真情况比较小,可以清楚地分辨压缩解压缩后的D-T2谱数据信息;当压缩比为52时,数据失真比较严重,难以分辨D-T2谱数据的信息。由以上的压缩比情况可知,在数据压缩解压缩后能完整保存原始D-T2谱数据信息的情况下,此压缩方法满足了规定传输速率下数据传输量要求。

图10 不同压缩比D-T2谱数据Fig.10 D-T2spectral for compression ratio
3.3 实测T1-T2谱数据在不同压缩比下的对比
图11为实测得到的回波数据经过反演后得到的二维T1-T2谱,其中二维CPMG自旋回波串的回波个数为4096个,反演得到的二维T1-T2谱由32×32个点构成。
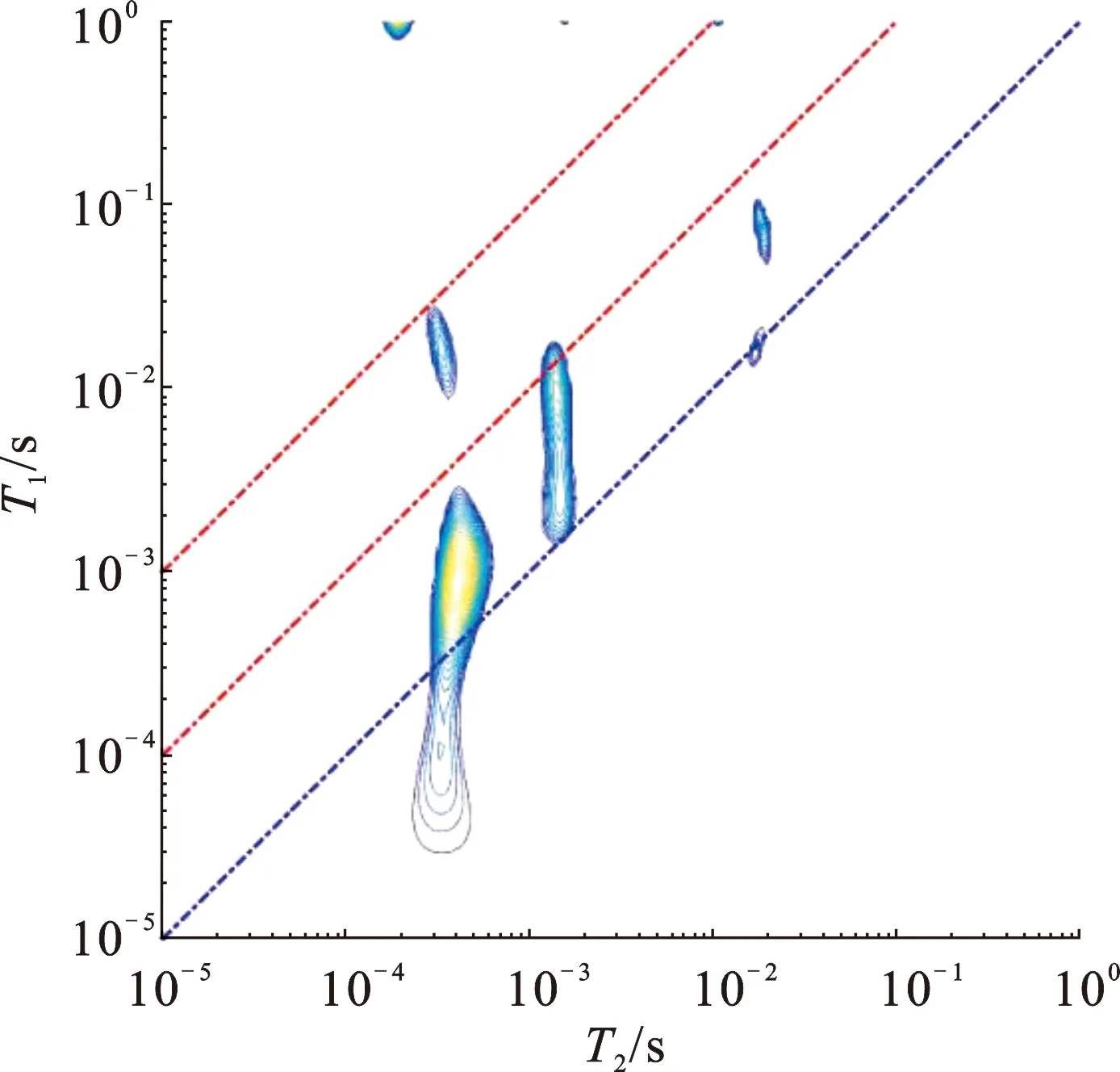
图11 原始实验T1-T2谱数据Fig.11 Raw experimental T1- T2spectral
图12为不同压缩比下原始的二维T1-T2谱数据经过压缩解压缩后的失真情况。由图12可知,当压缩比小于39时,可以保证原始数据在压缩解压缩后数据失真情况比较少,能清楚地分辨T1-T2的信息。当压缩比为48或者更大时数据失真比较严重,难以分辨T1-T2谱的信息。由以上压缩比情况可知,在数据压缩解压缩后能完整保存原始的T1-T2谱数据信息的情况下,此压缩方法满足了规定传输速率下数据传输量要求。

图12 不同压缩比T1-T2谱数据Fig.12 T1-T2spectral for different compression ratio
4 结束语
针对由于井下传输速率较慢导致核磁共振测井数据实时上传较难的问题,根据井下仪器的特点,设计了适用于FPGA实现的压缩解压缩算法。对设计的算法进行了较为详细的验证。测试结果表明,在可以准确地反映原始谱数据信息的条件下,进行压缩后的数据量能够满足井下数据实时上传的要求并有效识别油水不同流体,因此解决了随钻核磁数据传输问题,证明了本文基于FPGA设计的数据压缩解压缩算法可行。在此基础上,将进一步考察噪音对压缩解压缩的影响,为该方法在井下应用打下坚实基础。

