基于可解释神经网络的非常规储层参数建模范式

张凤姣, 邓少贵, 陈 琰, 高贝贝

(1.深层油气全国重点实验室,山东青岛 266580; 2.深层油气探测技术与装备教育部工程研究中心,山东青岛 266580; 3.山东省深层油气重点实验室,山东青岛 266580; 4.深层油气教育部重点实验室,山东青岛 266580; 5.中国石油青海油田分公司,甘肃敦煌 736202)

随着勘探开发的不断深入,中国已进入非常规油气时代的快速发展阶段[1]。储层参数是有效筛选油气甜点的重要参考,其精确量化的关键在于用岩石物理实验数据刻度常规测井资料,深入挖掘岩石物理实验数据与测井参数之间的复杂联系,建立连续深度的储层参数剖面[2]。针对非常规油气藏储层非均质性较强,储层参数建模困难的问题,许多学者将机器学习应用于参数建模中,在一定程度上提升了模型精度[3-7]。然而,大多数的机器学习模型都具有“黑盒”特性,其内部的决策过程不易被人理解,降低了模型的可信度。因此,亟待提出一种基于可解释机器学习方法的储层参数建模范式,在保证储层参数预测精度的同时,增加建模过程的透明度和可解释性。Castillo等[8]提出的泛函网络(functional network, FN)作为神经网络的广义高级形式,可以很好地平衡预测性能和模型的可解释性,已被广泛地应用于非线性回归和分类问题[9]、时序数据的建模预测[10]、微分方程的求解[11]以及油藏中的参数预测[12-13]等。笔者以岩石物理实验数据和测井数据建模问题为驱动,基于泛函网络结构建立一种可解释的神经网络(interpretable neural network, INN)作为储层参数建模范式,并以松辽盆地青山口组青一段5口探井的82块岩心样品的脆性指数可视化建模过程为例,对比其他3种经典机器学习算法的建模效果。

1 可解释神经网络

可解释的神经网络模型基于泛函网络框架建立,具有内置的解释机制。(x1,…,xd)为输入自变量,yj(x)为输出因变量,可以近似为以下形式:

(1)

式中,wim为训练后每个神经元的权值;Mi为第i个变量基函数的阶数;d为输入变量个数;φim(xi)(m=1,…,Mi)为第i个变量的基函数,常用的基函数包括多项式函数、指数函数、三角函数及其混合基函数,基函数的选择根据先验数据信息而定。

图1为简化的使用神经网络符号表示的可解释神经网络架构。输入层是包含d个节点的单连接层,每个输入节点都服从归一化(N),输入层每个节点的输出将作为下一层子网络的输入。子网络用来训练确定基函数φim(xi)的最终形式及其系数wim,利用现有的数据进行最优参数学习。得到的基函数输入到输出层,最终采用线性激活函数(∑)激活输出。

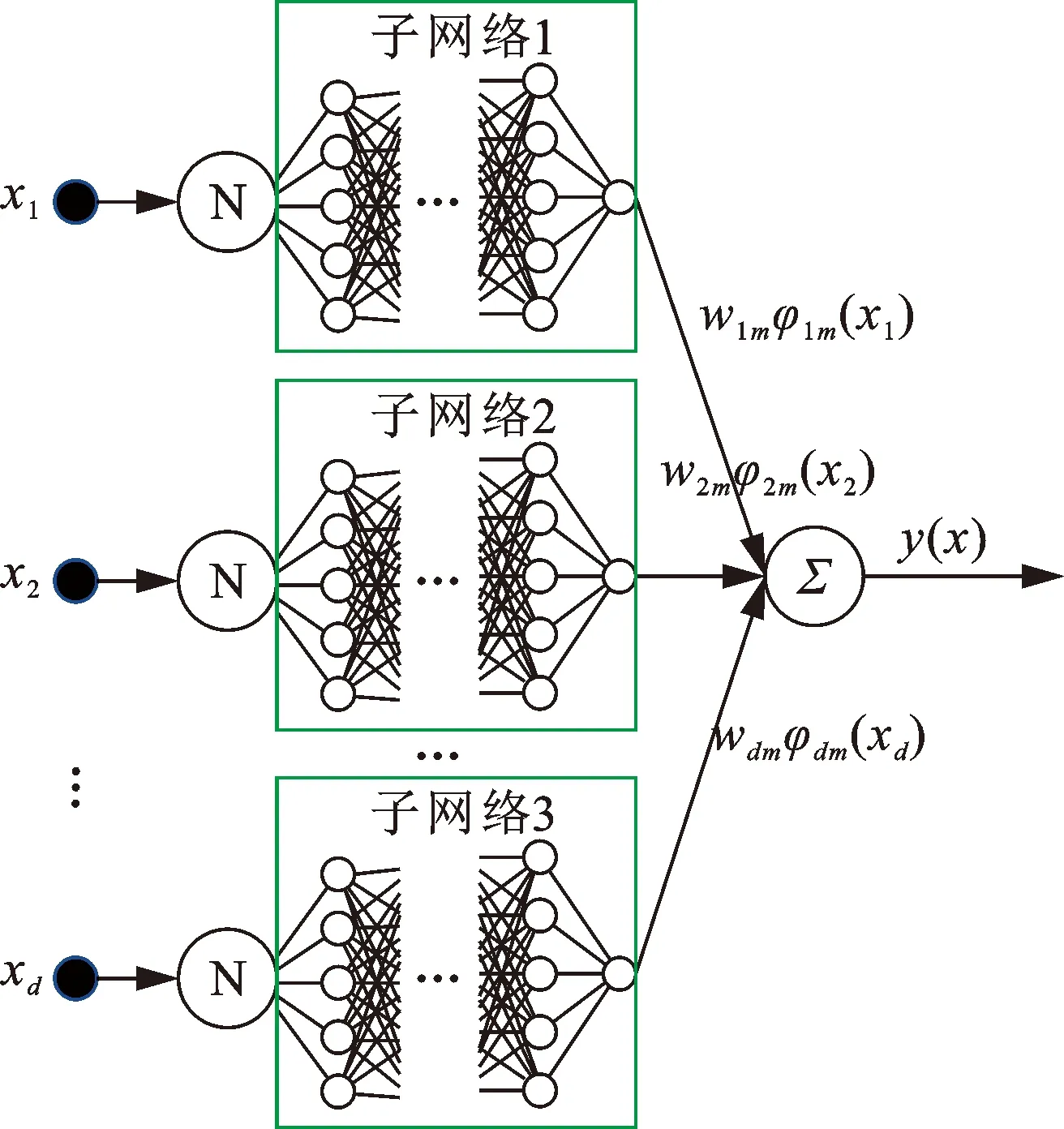
图1 可解释神经网络(INN)架构Fig.1 Interpretable neural network (INN) architecture

1.2 模型参数优化

确定INN基本结构后,需要估计网络参数以得到最优模型,本文中利用变分贝叶斯逼近方法对模型进行学习。变分贝叶斯方法(variational Bayesian, VB)[14]近年来由于其计算量较少,收敛速度较快、泛化能力较强等优点已被广大学者应用到模型参数估计问题。为了逼近方程(1),假设观测变量D={((x1,y1),…,(xN,yN)}),x为d维向量,θ为一新的系数向量,α为系数精度参数,β为噪声精度参数,且α和β后验概率分布函数均符合Gamma分布函数,则观测变量的边缘似然函数满足:

logp(D)=+KL(q‖p).

(2)

其中

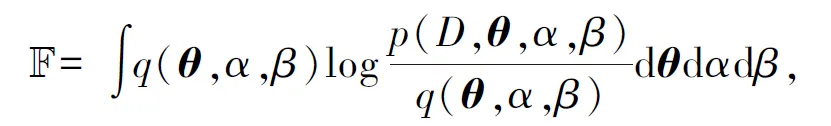
1.3 建模范式流程

所提出的基于可解释神经网络的岩石物理实验数据与测井信息关系的建模范式主要包括4部分,即输入参数选择、初始网络结构确定、最优模型选择以及模型测试(图2,其中GR、SP、AC、DEN、CNL、RLLD、RLLS分别表示自然伽马测井、自然电位、声波时差、密度测井、中子孔隙度测井、深侧向电阻率、浅测向电阻率),其中绿色部分代表储层参数为脆性指数IB时的必选项。图2只是采用INN建模范式的一般流程,还存在许多可以改进的方面,比如丰富基函数库的内容,使其可以逼近更复杂的非线性关系;建立多种最优模型选择方法,提升计算速度和精度;不仅仅局限于脆性指数的建模,可适当扩展储层参数模型库。

1.4 模型可解释性

预测模型的可解释性主要体现在以下两点:①传统神经网络结构在调整隐含层的链接权重时将所有测井输入数据混合,无法评估单个测井数据的贡献,而可解释网络可以捕获单条测井曲线与岩石物理数据间的相互作用;②在传统神经网络中,只有链接测井输入数据的权可以从训练中学习得到,神经元函数是固定的,而可解释网络各层的神经元函数选择更为灵活,各网络层基函数形式不断组合变换直至得到最优排列形式。为此,本文中通过引入泛函网络,使用非线性基函数逼近期望数值,在对各子网络训练过程中通过可视化基函数及各权重系数,获得每个测井系列与目标值的关系,从而一定程度上实现了模型的可解释性。

2 INN模型应用

2.1 数据背景

脆性作为页岩储层的重要参数之一,可以用来表征岩石在水力压裂过程中形成复杂裂缝网络的能力,脆性高的岩石在外力作用下更容易发生脆性变形,形成丰富的次生裂缝网络,这对页岩油产业的产能提升起到了重要作用[15]。前人已经提出了多种页岩脆性的定量表达式,原理主要是基于应力-应变响应分析、弹性模量和泊松比等力学参数表征以及页岩矿物组分分析[16-17]。选取松辽盆地青山口组青一段5口探井的共82块岩心样品的X-衍射(XRD)实验数据计算脆性指数,取芯层段多发育暗色油页岩、砂岩和粉砂岩互层,油气显示活跃。图3展示了部分样品的矿物组成,包括石英、长石(钾长石、斜长石)、方解石、铁白云石、菱铁矿、黄铁矿和黏土矿物。其中长英质矿物(石英、长石)含量最高,质量分数为22%～86%,平均为54.22%;其次是黏土,质量分数为4.3%～46.3%,平均为31.6%;除上述两种主要矿物外,碳酸盐(方解石、铁白云石)含量也相对较高,质量分数为0～71.1%,平均为9.28%。据前人对页岩岩石物理性质的研究,页岩油储层脆性矿物可以包括石英、长石和碳酸盐矿物[18-19]。因此根据XRD矿物组成可以计算出样品的脆性指数IB,计算公式为

图3 部分岩心矿物成分组成Fig.3 Mineral compositions of cores

IB=(wfel+wcarb)/wtot.

(3)

式中,wfel为长英质矿物的质量分数;wcarb为碳酸盐岩的质量分数;wtot为所有矿物的质量分数。

2.2 测井数据选择

研究表明,自然伽马测井(GR)、密度测井(DEN)、声波测井(AC)、中子孔隙度测井(CNL)、深侧向电阻率测井(RLLD)和浅侧向电阻率测井(RLLS)对脆性最为敏感,且石英和碳酸盐岩含量越高,GR和AC越低,电阻率和DEN越高[20]。通过分析脆性指数与各测井曲线交会图(图4(a)～(e)),DEN、AC、CNL、RLLD和RLLS与脆性指数存在一定的相关性,其规律与现有研究相符,而GR和脆性指数的相关性较差,分析是因为研究区样品含有的长石具有放射性,故GR曲线对于黏土矿物的反映存在误差,导致GR与脆性之间相关性较差。因此选择DEN、AC、CNL、RLLD和RLLS 5条测井曲线作为输入。表1列出了输入参数的统计特征及其与脆性指数(IB)的相关系数平方(R2),其中AC对于IB的影响作用最大,其余依次是CNL、RLLD、RLLS和DEN。

表1 测井参数特征及与IB的关系Table 1 Logging parameter characteristics and relationship to IB

2.3 模型可解释结果

通过测井数据特征与脆性指数关系分析结果作为先验信息,二者之间存在多项式函数关系,因此选择多项式(1,x,x2,…,xM)作为初始基函数。针对页岩脆性指数预测,随机抽取70%的数据作为训练集,30%的数据作为测试集,将5条测井曲线输入到5个子网络中进行网络训练,最终得到最优模型。模型选择过程主要是确定各子网络基函数的阶数,Bayes information criterion (BIC)准则同时考虑了模型的预测精度和复杂度。本文中选择BIC准则作为贝叶斯可解释神经网络的模型选择方法,BIC函数值最小时,所对应的模型参数最优。BIC准则[21]可以表示为

(4)

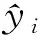
当EBIC=286.21时模型性能最佳,此时子网络的非线性变化过程如图5所示,图5(a)分别展示了以归一化的AC、CNL、DEN、RLLS和RLLD作为变量的基函数φim(xi),图5(b)分别展示了各基函数的权重分布wim。表2列出了各基函数的数学表达式。可以看出,脆性指数与AC、CNL和RLLD之间均存在二次函数关系,基函数RLLD的系数均为正数且数值较大,AC和CNL的系数分布相似,阶数越大,对应的权重绝对值越小;IB与密度和浅侧向电阻率之间关系更为复杂,为三次函数关系,基函数DEN的阶数与系数的绝对值成正比。至此,各测井系列与脆性指数的复杂非线性关系凝练为一数学公式,神经网络的“黑盒”成功变为“白盒”,可供无人工智能基础背景的地球物理学者快速高效地建立储层参数模型。

表2 模型解释结果Table 2 Model interpretation results

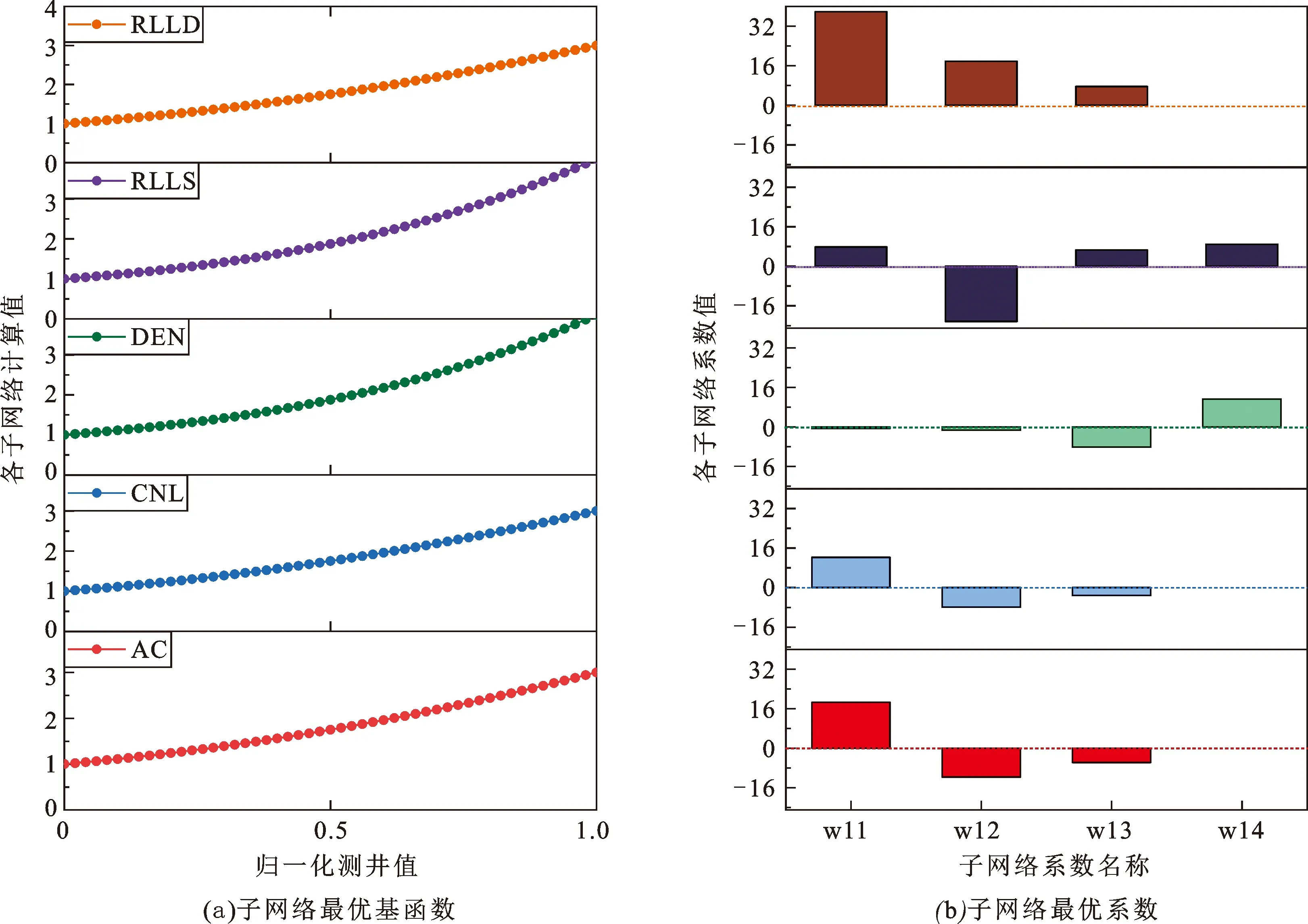
图5 模型可视化结果Fig.5 Model visualization results

2.4 模型精度对比

2.4.1 评价指标

采用均方根误差ERMS和Pearson相关系数R来反映机器学习模型的性能:

(5)

(6)

式中,yi和pi分别为脆性指数实际值和预测值;N为样本点数;D为方差;Cov(Y,P)为协方差函数,表示变量Y与变量P之间相互关系的特征。ERMS越小,R越高,模型性能越好。

2.4.2 预测结果

为了证明所提出的INN网络不仅具有可解释性,还保障了相对高的预测精度,对比分析了极限学习机ELM、支持向量机SVM及BP神经网络3种经典机器学习方法在页岩脆性指数预测结果。为了增加试验的可信度,4种机器学习方法均采用随机划分得到的训练集和测试集数据建模,且每个模型均进行了10次重复试验,其中INN模型参数采取由2.3中所得到的最优化基函数及其系数。图6(a)、(b)分别展示了4个模型10次试验结果的误差ERMS和相关系数R的分布,INN模型的ERMS分布在5.2%～6.31%,平均为5.66%,R为0.75～0.87,均值为0.83;ELM模型的ERMS为5.62%～12.29%,平均为8.75%,R为0.33～0.78,平均为0.57;SVM模型的ERMS分布于5.72%～8.88%,平均为7.1%,R为0.49～0.82,平均为0.69;BP神经网络的ERMS为6.63%～10.08%,平均为8.09%,R介于0.15～0.76,平均为0.58。

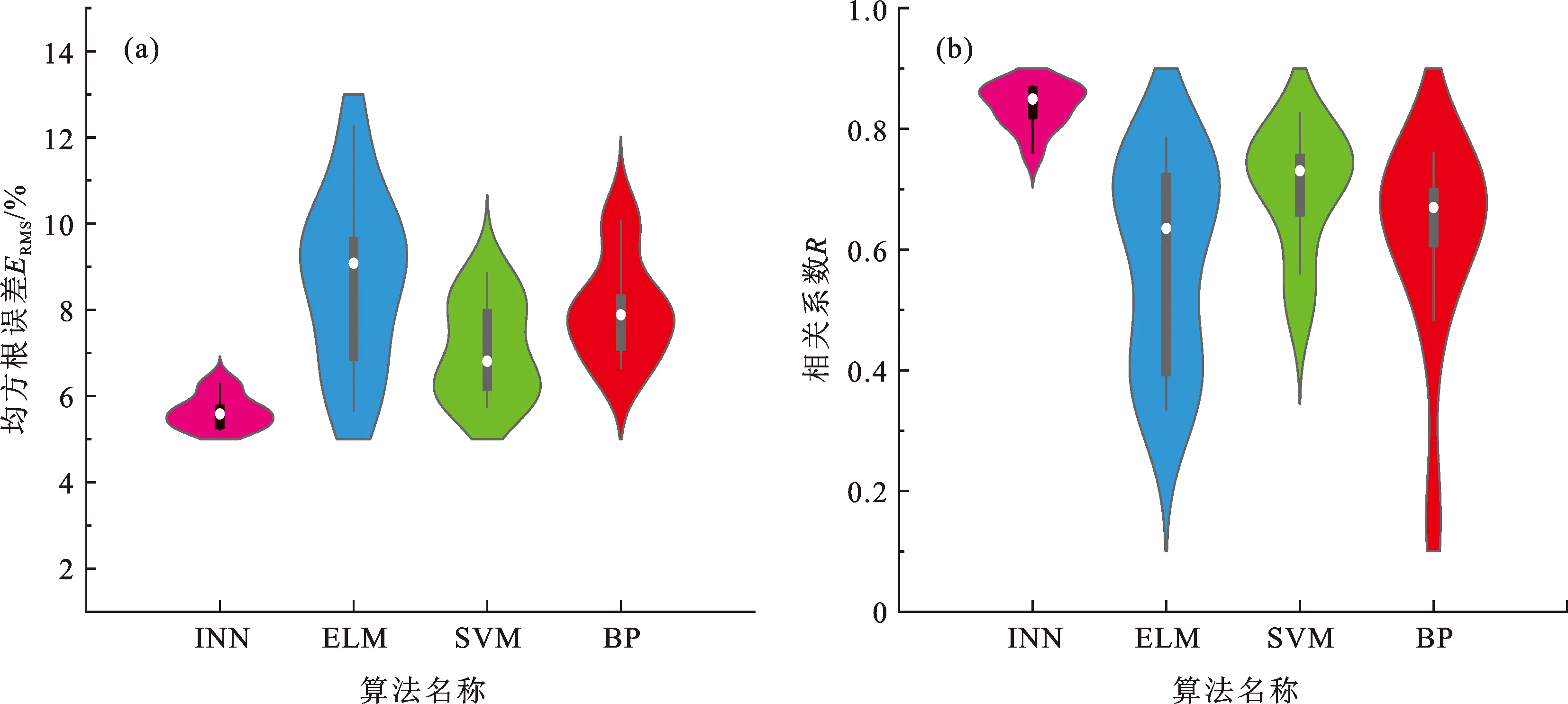
图6 四种机器学习算法10次试验结果误差分布Fig.6 Accuracy distribution of 10-trial results of four machine learning algorithms

可以得出,INN模型的精度和稳定性均达到最优;ELM、SVM和BP由于数据量较少,泛化能力弱,都存在一定程度上的过拟合问题,其中ELM模型的预测精度和稳定性最差,其次是BP和SVM。

2.5 实例应用

以来自松辽盆地青山口组的井A作为研究对象,将所建立的可解释神经网络模型和极限学习机ELM、支持向量机SVM、BP神经网络4个储层参数预测模型推广应用于全井段参数建模中。其中针对研究区脆性指数的INN模型最终结果可直观地展示,可在不使用人工智能软件的情况下快速高效地计算储层参数,这也是本文中所提出模型区别于普通机器学习算法的一大优势,INN模型表示为

(7)

式中,N为样本点数;ε为误差估计值,实际应用中可忽略不计。

图7为井A脆性指数预测结果的连续剖面。可以看到,在电阻率曲线和三孔隙度曲线剧烈变化的层段(如深度2079 m和2112.5 m处),ELM、SVM及BP神经网络3种经典机器学习方法的收敛性明显不足,ELM和BP预测曲线变化过于剧烈,而SVM模型的预测结果几乎呈现一条平缓的直线。基于岩心岩石物理实验的小样本数据条件下,且当储层参数与测井数据之间的非线性关系较强时,普通的机器学习模型难以从有限的数据中挖掘出正确的映射关系,方法收敛性差,精度难以保证。本文中提出的可解释神经网络的预测结果与岩心实验数据有着很好的吻合性,变化趋势可靠性强,进一步证明了所提出模型的可行性和有效性。预测得到的脆性指数剖面结合其他储层参数,为后续页岩油储层的勘探开发提供技术思路。

图7 井A储层参数预测结果Fig.7 Reservoir parameter prediction results of well A

3 结束语

本文中基于泛函网络结构建立了一种可解释的储层参数预测模型,其关键在于可视化各子网络基函数及其最优系数,对测井曲线和储层参数之间的非线性关系具有一定程度的解释性,相较于机器学习的“黑盒”性质具有更加可靠的参考和应用价值。普通机器学习模型(如ELM、SVM、BP)的精准度是建立在大量数据的基础之上的,而在实际工程应用中很多时候仅有少量岩心实验数据参与储层参数建模,此时普通机器学习算法难以准确挖掘出小样本数据之间的内在联系,泛化能力不足。基于可解释神经网络得到的简单的经验关系式,稳定性强,准确率高,一旦测井曲线与储层参数的关系确定,便可不再依赖人工智能软件进行推广应用。