复杂环境下多飞行器的优化人工势能场运动规划算法
刘婳婳 王东辉 钱佳程 孟 瑶 宣建强
(上海宇航系统工程研究所,上海 201109)
0 前言
人工势能场(Artificial Potential Field,APF)算法在运动规划中的应用范围较广[1]。而在实际问题中,客观存在许多动态不确定性,这些因素能否得到有效处理,将直接影响规划效果。经过多年的发展,许多研究人员为这一课题做出了巨大贡献[2-3]。然而,APF 理论和方法在一些方面仍有优化的空间,例如新模型的构建、详细参数的设置、理论的优化和更新等。此外,APF 方法在复杂条件下也存在一定的缺陷[4-5]。
研究人员主要通过与其他算法的结合或模型函数优化对传统APF 算法进行优化[6-8]。赵炳巍等[7]采用模拟退火算法求解局部极小值,存在收敛慢、随机性等问题。顾育津等[8]给优化后的函数引入1 个额外的控制器,以避免局部最小困境,但是当移动代理接近密集障碍环境时,仍会发生抖动。该文研究了一种在三维复杂静态、复杂动态环境中,考虑相对速度、距离以及转向角的优化的多飞行器APF 运动规划算法,该算法可以以平滑的路径摆脱局部最小困境。
1 APF 局部最小困境和路径振荡的优化
如图 1 所示,APF 方法的基本原理为将工作环境中移动代理的运动视为在接收不同潜在场力的影响下的运动过程,势力场对应的坐标点如图2 所示。目标点在整个移动代理的工作环境中生成吸引场UG(如公式(1)所示),将飞行器从原始区域引导至目标区域,而障碍物在一定范围的影响半径d0内产生排斥场UO(如公式(2)所示),所得合势能场U(如公式(3)所示)可以通过其在当前位置接收的所有排斥势能场和吸引势能场的叠加来获得,飞行器在引力和排斥力的作用下运动,二者的合力就是移动飞行器的加速力,方向即为飞行器的移动方向[8]。

图1 势能场示意图
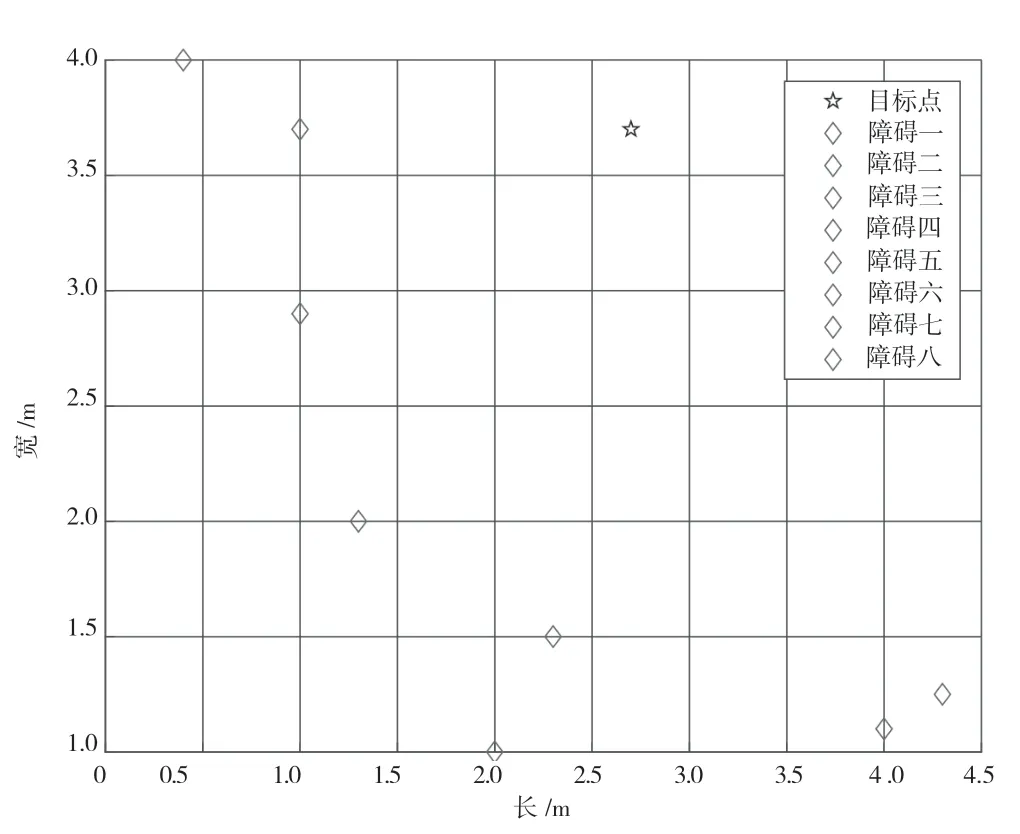
图2 势能场对应的坐标点
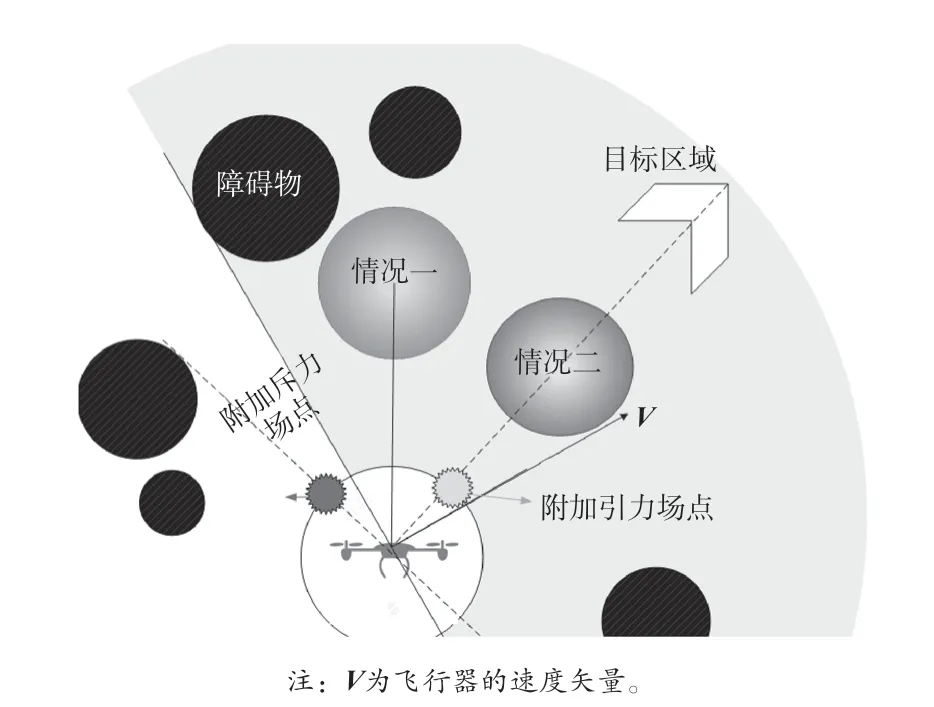
图3 附加斥力和引力势能场点
式中:UG为目标点在整个移动代理的工作环境中生成的吸引场;Xi为飞行器i的位置;kG为吸引力增益因子;d为飞行器i至目标地的距离;XG为目标G的位置。
式中:UO为障碍物在一定范围的影响半径d0内产生的排斥场;kO为当飞行器和障碍之间的距离;XO为障碍所处位置;d0为影响半径;U为合势能场。
选取我院2017年6月~2018年6月47例行人工髋关节置换术患者的临床资料,男29例,女18例,年龄59~91岁,平均(73±3.5)岁,股骨颈骨折19例,老年性退行性骨关节炎11例;单股骨头置换术7例。
在复杂的环境中,前方区域或目标区域周围可能存在多个密集障碍物。如果来自周围障碍物的排斥势能场大于来自目标区域的吸引势能场,那么飞行器在到达目标区域之前无法继续向前移动,即落入局部最小区域。也就是说,当飞行器的方向偏离目的地的方向超过90°或者在当前状态和相邻时间的状态的变化接近0 时,可以判定运动规划陷入了局部最小困境。如公式(4)所示,引入飞行器当前位置和目标区域之间的距离因子,以提供一个排斥力,从而逃离局部最小点,打破吸引和排斥相互抵消的状态。
式中:Ua为附加场。
新的总势场U1如公式(5)所示。
分析:There was significant difference between the audio and video groups when image and sound were strongly mapped semantically
推动农业知识产权服务普及化,为创新创业团队提供知识产权的服务是培养“三农”知识产权创新团队的意义。首先,可提升学生对知识产权运用、运营的基本能力,使其掌握知识产权产生和转化的过程,激发农业高校学生的创新创业动力。其次,将团队对知识产权工具的运用能力转化为服务产业,将科技创新和创业有机结合起来,形成经济效益,提高科研转化率。
除此之外,还需要进一步考虑障碍物、飞行器和目标区的共线性问题。简单地引入吸引距离因子会引起飞行器与共线障碍物的碰撞或振荡。如图 3 所示:1) 情形一。当确定飞行器处于局部最小状态且存在障碍物时,飞行器与目标区域不共线,在飞行器周围设置较小范围的完整边界,并在飞行器与目标方向的边界处增设1 个吸引势能场点,飞行器被吸引离开局部最小陷阱。2) 情况二。当判断飞行器处于局部最小状态时,障碍物与飞行器、目标处于共线状态,如果在飞行器指向目标区的方向放置额外的吸引势能点,就会与共线障碍物进行碰撞或引起路径抖动的问题。因此,在完整区域边界垂直于飞行器指向目标区域方向的位置增设1 个附加斥力势能点。为了避免飞行器落入复杂障碍物区域,将附加的斥力势能场放置在斥力势能场较多的方向,推动飞行器向更简单的势能场方向移动。如果飞行器方向相对目的地方向小于90°,那么可以确定飞行器路径规划逃脱了局部最小困境。因此,增强型APF 算法U2如公式(6)所示。
构造一个具有多个障碍物的二维复杂环境,使其出现如图 4 所示的局部最小困境,以验证该优化算法的有效性,仿真结果如图5 所示。由图5 可知,考虑距离因素的U1(Xi)APF 运动规划算法可以逃脱多障碍物的局部最小值陷阱,但是会陷入共线局部最小值条件,抖动严重。而加入附加势能场的U2(Xi)APF 运动规划算法成功地摆脱了共线条件下的局部最小值困境,但是仍存在路径不平滑抖动的问题。最终优化的U3(Xi)APF 运动规划有效地避免了势能场的过度变化,整个路径相对平稳,不会陷入各种局部最小值问题。
综上所述,为了提高国土资源所档案管理工作的水平,使其能更好地适应时代发展,更好地服务于经济建设,建议国土资源所档案管理从以下几个方面加以改进。
为了高起点、高标准地规划建设淮安生态新城,淮安市政府提出要将生态新城建设成生态示范区、绿色建筑示范区的目标。水系规划在满足区域防洪、排涝、灌溉要求的前提下,如何充分体现“绿色、生态”的建设理念亦成为规划难点之一。
式中:UO1为改进排斥场一;ρα为距离因子;α为距离因子系数,α∈(0,1);XG为目标所处位置。
此外,势能场的复杂性导致势能场的变化过大,而当前状态受势能场变化的影响,导致运动角度变化过快,运动规划就会出现震荡。如公式(6)所示,可以采用削弱势能场、减缓相邻2 个运动状态变化率的方法减轻势能场变化过大或变化太频繁所带来的影响。当2 个相邻飞行器运动轨迹的夹角连续超过90°时,可以判定为剧烈势能场变化。此外,为了进一步减少计算量、降低势能场的复杂性,确定基于飞行器飞行方向的±90°为有效边界,并消除距离外的障碍物和相应的斥力场冲击,使势能场变化强度变小,从而获得新的排斥场UO2,如公式(7)所示。
新的APF 长为U3,如公式(9)所示。
税收活动不仅是中国单方面的责任,也是共同合作的各个国家之间的共有责任。因此中国在税收征管方面为了更好地服务于国内企业和其他国家,制定了相应的国际税收协定并与之谈签,在实现税收征管服务的公平性的同时也加强了贸易合作。
式中:λ为步长调整系数。
式中:Δθ为相邻运动时刻变轨的转角。
式中:UO2为改进斥力场二。
当Xo=(xo,yo,zo)T大于影响半径d0的排斥增益因子时,定义排斥场UO=(xi)=0。
在3 mm厚的XLPE薄片上截取6片边长50 mm、厚度3 mm的正方形XLPE薄片,将6片样本分为A、B、C三组。其中样本1、2属于A组,样本3、4属于B组,样本5、6属于C组。之后选取3组样本正中间的圆形区域(直径25 mm)作为水树老化区,采用注射器针头在此区域制作3行平行的针孔缺陷(针孔深度1.5 mm)。注射器针头的参数如下:
这台缝纫机,从我记事起就陪伴着母亲,就如母亲的孩子。可能是经常使用的缘故,机头的轮子上,手常常拽摸的地方,镀铬膜已经脱落了,露出花花点点的底色,显得十分老旧。传动轮上小拇指粗细的环形皮绳,已经被岁月打磨得粗细不均,似乎随时都会断开。缝纫机台板上的木纹依然清晰光洁,但铁制的压角和底盘已经凹凸不平,那深深浅浅的划痕,都在无声地诉说着母亲那逝去的岁月。
Δθ越大,对相应的排斥势能场的削减程度就越高。同时,动态调整电流步长n,以减缓势能场的剧烈变化。此时,如公式(8)所示,设置步长n'随着旋转角度的增大而变慢,路径变化更平稳。

图5 优化U1(Xi)、U2(Xi)和U3(Xi)APF 算法的比较
2 三维条件下增强的多飞行器APF 算法
2.1 优化的三维APF 动态避碰算法
针对飞行器在三维复杂环境下的运动规划问题,该文进一步推导了优化算法(APF 算法一般采用等步长算法)。事实上,飞行器的运动速率是可变的,鉴于飞行器的状态随着势能场U3(X)的变化而变化,因此,将此运动规划优化为机动速度Vi的迭代更新,如公式(10)所示。
式中:λ'为机动速度调整系数;n为设定步长;V为当前机动速度。
构建三维复杂多障碍物周边环境,对可能出现的局部最小困境和路径震荡问题进行验证,仿真结果如图6~图8 所示。由图6~图8可知,U1(Xi)的算法陷入了局部最小值困境,出现了严重的抖动。附加势能场的U2(Xi)算法可以成功摆脱局部最小的困境,但是仍然存在路径抖动不均匀的问题。最终优化的U3(Xi)算法可以有效地避免势能场的过度变化。在去除不必要的障碍势能场后,飞行器沿整个势能场的相对简单方向运动,路径相对平滑,不会陷入局部最小问题。
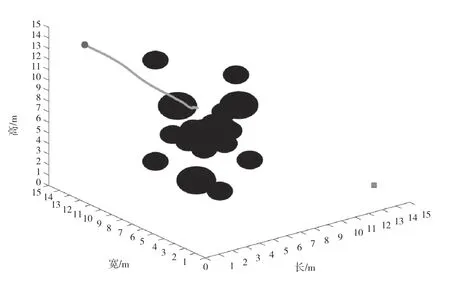
图6 U1(Xi)APF
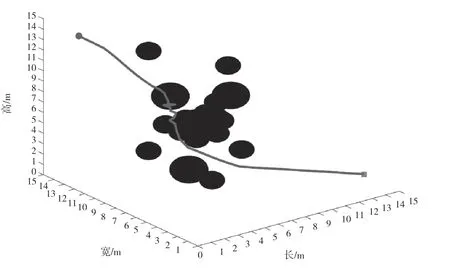
图7 U2(Xi)APF

图8 U3(Xi)APF
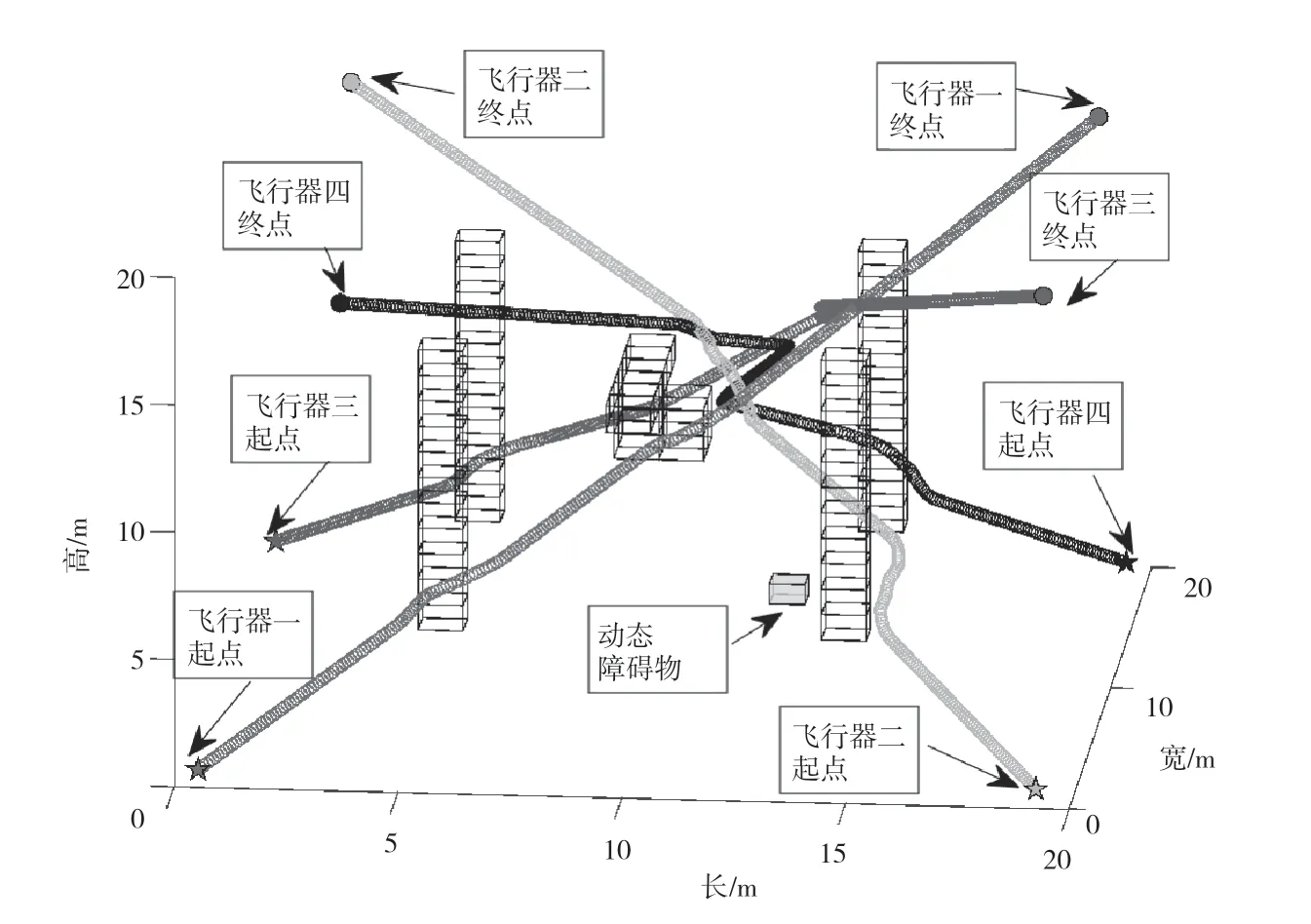
图9 三维复杂条件下多飞行器的优化型APF 轨迹
此外,考虑动态障碍物,需要同时引入相对距离和机动速度信息,并加入相对机动速度因子,构建增强的排斥场函数如公式(11)所示。
式中:UO3为构建的新势能场;V为移动障碍物与飞行器的相对机动速度矢量;XV为动态障碍物的位置;β为增益系数。
因此,构建的新势能场UO3将包括飞行器与障碍物的相对距离和机动速度信息。
2.2 三维复杂环境下的优化多飞行器APF 算法
当多架飞行器在同一复杂环境下同时执行任务时,应考虑飞行器之间的避撞。在飞行器周围设置避碰区域,如果2架飞行器进入对方的避碰区域,它们将对方视为动态障碍。飞行器之间的排斥场函数Vij如公式(12)所示。
式中:A为排斥增益因子;Xi、Xj为飞行器i和飞行器j的位置矢量;ρa为飞行器间的避碰区域范围;V(Xi,Xj)为飞行器i和飞行器j之间的相对机动速度矢量;ρ为欧几里得距离;γ为飞行器的相对速度因子。
复杂环境中多飞行器的优化APF 函数U4如公式(13)所示。
如图 9 所示,在多障碍物和动态障碍物的复杂环境中,相验证了优化多飞行器APF 运动规划的可行性。仿真结果表明,多飞行器可以在具有多个静态和动态障碍物的复杂环境中避障和防撞,并以平滑的路径成功到达目标区域。
3 结语
该文提出了一种基于三维复杂静态和动态障碍物条件的优化多飞行器APF 运动规划算法,该算法考虑了相对速度、相对距离和转向角,能够以平滑的路径避开局部最小值,动态调整步长和排斥势能场。同时,设置障碍物的有效边界约束,以降低势能场的复杂性。仿真结果表明,优化后的算法能够以平滑的路径避开局部最小陷阱。

