考虑客户满意度及飞行限制的无人机冷链配送路径优化问题
李诗茵 (浙江理工大学 经济管理学院,浙江 杭州 310018)
0 引 言
近年来,随着冷链物流的发展和客户黏性的降低,消费者对生鲜产品配送的及时性提出了更高要求。如何在降低生鲜产品运输成本的基础上增加顾客的满意度,是生鲜产品运输亟待解决的问题。为此,本文展开了对冷链物流路径优化的研究。
车辆路径问题(VRP)由Dantzig和Ramser于1959年首次提出。近年来,国内外众多学者对冷链物流VRP问题进行了广泛研究。季琳琳等提出以成本与满意度为双目标的冷链水果运输模型[1];李倩等考虑客户满意度,以货损成本、惩罚成本等综合配送成本最低为目标函数,构建了一个多目标配送路径优化模型[2];任腾等以车辆载重、客户时间窗和冷链产品变质率为约束,构建在客户服务时间范围内以碳排放量最小为优化目标的冷链车辆路径优化模型[3]。考虑到生鲜产品的易腐性及生鲜配送的时效性,本文引入模糊梯形函数来刻画软时间窗下的客户满意度并构建相应的惩罚函数。
在道路资源日益紧缺的社会背景下,国内外对城市交通管制给车辆配送的影响已有一定研究[4-6]。而在考虑飞行限制的无人机配送研究中,Jeong考虑了包裹重量对无人机能耗的影响和受限飞行区域,并提出了一种两阶段构造和搜索启发式算法。目前,有关限飞区等飞行限制对无人机路径影响的相关研究仍处于起步阶段,但是随着无人机物流逐步走进人们的日常生产生活,考虑飞行限制对无人机配送的影响而对配送路径进行优化,对于提高无人机物流配送效率及客户满意度有着重要意义。因此,本文考虑了临时限飞区及永久限飞区对物流路径规划的影响,并综合考虑客户满意度,以无人机载荷限制和飞行距离限制等为约束,构建成本最小化及客户满意度最大化的双目标数学模型并探寻求解算法。
1 问题描述
本文旨在探讨在生鲜配送中心利用多架无人机向多个客户点进行直接配送的情况下,如何在保证配送总成本最小和客户满意度最大为双目标的前提下,建立成本函数模型。由生鲜产品的新鲜度及每个客户点的服务时间窗共同决定了客户的满意度。由于在任意两个客户点之间都可能存在因城市管制或极端恶劣天气导致的限飞区,因此无人机应在前往下一个客户点进行配送服务前,根据模型决策选择是否需要绕飞或等待,若需要绕飞,则应重新进行路径规划。
本文在满足客户点需求、客户时间窗、无人机飞行限制约束等条件下,设计出使总成本最小及客户满意度最大的混合整数规划模型,模型如下:
约束条件:
式(1)、式(2)表示模型的双目标函数;式(3)表示无人机的飞行距离限制;式(4)表示无人机的载荷重量限制;式(5)、式(6)表示每个客户点均得到配送服务且仅仅被服务一次;式(7)表示从生鲜配送中心出发前往客户点的无人机数量即为派遣的无人机数量;式(8)表示无人机的耗费时间;式(9)表示配送过程是连续的,且不考虑无人机在客户点的服务时间;式(10)表示无人机在限飞区的等待时间。
2 绕行决策
对于永久限飞区及长达数小时的临时限飞区,无人机有时无法按照原定的直线配送路径飞行。考虑到在实际配送中,由于无人机绕行会产生额外的飞行成本,并且绕行增加的飞行时间有时会大于等待时间,导致客户满意度惩罚成本的增加,因此,本文考虑无人机在限飞区内的飞行时间与限飞区的限飞时间重叠的情况下,无人机可根据配送成本来选择等待或绕道飞行限飞区。
为了更好地规划无人机的绕行路径,首先,对客户点之间的限飞区进行统计;然后对限飞区域按照永久限飞区及临时限飞区进行划分。对于永久限飞区,无人机只能选择绕行;而对于临时限飞区,无人机需要进一步根据限飞时段及成本耗费确定等待或绕行决策。
现有研究中,对于绕行限飞区,往往采用沿原配送路径飞至限飞区,而后旋转绕行该区域的方式。基于该方式,本文对绕行路径进行了优化,在绕行避过每个限飞区时,无人机先沿着限飞区的外切线路径飞至限飞区边缘,随后可选择沿限飞区的左侧或右侧旋转飞行以避开无人区。若无人机经过的限飞区数量为m,则无人机共有2m种可能绕行路径。
若无人机按直线路径到达限飞区的时间晚于限飞区的结束时间,或无人机离开限飞区的时间早于限飞区的开始时间,无人机可按原拟定路径飞行,无需绕行或等待;对于其他情景,无人机对等待及绕行情况的成本进行比较,从而做出等待或绕行决策。式(11)、式(12)用来判别限飞区是否需要做出绕行或等待的决策。
3 算法设计
3.1 混合遗传算法设计
由于遗传算法直接对结构对象进行操作,不存在求导和连续性限制,并且具有较好的稳定性和全局寻优能力,因此被广泛应用于VRP问题的求解中,但是存在局部搜索能力差和早熟收敛等问题。大型邻域搜索算法通过在当前解的多个邻域中寻找更满意的解,能够极大地扩大算法在解空间的搜索范围,但是时间成本较高。模拟退火算法能有效避免优化过程中陷入局部最优解,但是算法的运行效率不高、进化速度较慢。将遗传算法与自适应大邻域搜索算法、模拟退火算法相结合,使用随机序列生成方法来构造初始解,通过算子间的相互竞争生成当前解的邻域结构,同时采用Metropolis准则接受差解,对染色体进行进化,可以大幅提升种群的多样性。同时,基于算法的精英保留策略,每次只会选择部分染色体参与进化,算法的求解时间不会过度增加。因此,本文设计的混合遗传算法可以有效地跳出局部最优解,以更大的概率获得全局最优解。
首先,对未被服务过的客户点进行随机排列,如果能够满足如下条件就将其按顺序依次放入可访问列表里面:
该客户点的货物重量不超过当前无人机的最大载荷重量;
无人机从配送中心出发访问完当前所有客户点并返回配送中心的距离不超过无人机的最大飞行距离限制。
得到的访问列表为空,表明当前路线已经构造完成,无人机就执行返回配送中心的操作。重复这一步骤,直至所有客户点均被服务过。
在计算开始时,每个算子都设置相同的权重和分值。在每次搜索过程中,破坏和修复算子的选择都基于轮盘赌规则,以此增加算子选择的多样性。根据算子的不同表现情况给予得分,得分越高表明算子的表现越好。算法所使用的破坏算子与修复算子如下:
破坏算子1,随机移除。随机选择该路径上的一个点进行移除,同时更新路径;
破坏算子2,距离最长移除。随机选择一条路径,移除对路径长度影响最大的点,以此缩短整条路径的长度;
修复算子1,随机插入。将随机移除的一个点随机插入一条路径内;
修复算子2,最优贪婪插入。随机选择一个点,判断该点插入某位置后该条路径的总成本增加值,选择成本增加值最小所对应的位置进行插入。
3.2 混合遗传算法步骤
混合遗传算法的具体步骤如下:
Step 1 初始化模型、算法的各项参数,如初始温度、初始算子权重、总循环次数、种群数目等,生成初始编码;
Step 2 采用随机序列生成初始解及编码;
Step 3 计算种群适应度,即总成本目标函数的倒数;
Step 4 根据精英主义选择前1/3的种群,采用自适应大邻域搜索算法,根据算子权重选择破坏算子与修复算子,破坏当前编码、修复被破坏的编码并生成新编码;
Step 5 根据模拟退火算法Metropolis准则以概率接受优解和差解进行当前解的更新;
Step 6 若新解优于最优解,则将当前解替换最优解;
Step 7 更新算子的分数及权重;
Step 8 更新种群并进行排序;
Step 9 判断是否达到迭代终止条件(总循环次数k达到K),若是,则算法停止计算,输出最优结果,若否,则跳转至Step3 。
4 算例分析
本文对某生鲜产品公司进行了调研,并对需要用到的相关数据进行收集和整理。
4.1 数据准备
本文对客户点相互之间及生鲜配送中心和客户点之间的距离均采用直线距离,该距离可根据客户和配送中心的坐标计算得到;然后再依次对单日内的100个客户进行编号,统计客户的需求量、客服期望的时间窗以及7个永久限飞区和33个临时限飞区的禁飞时段。本文将配送中心开始进行配送的时间6:00用0表示,在此基础上将日常的时钟时间转化成数字,比如8:30用150进行简化处理。最后,设置配送无人机的属性及货物的相关参数,如表1所示。
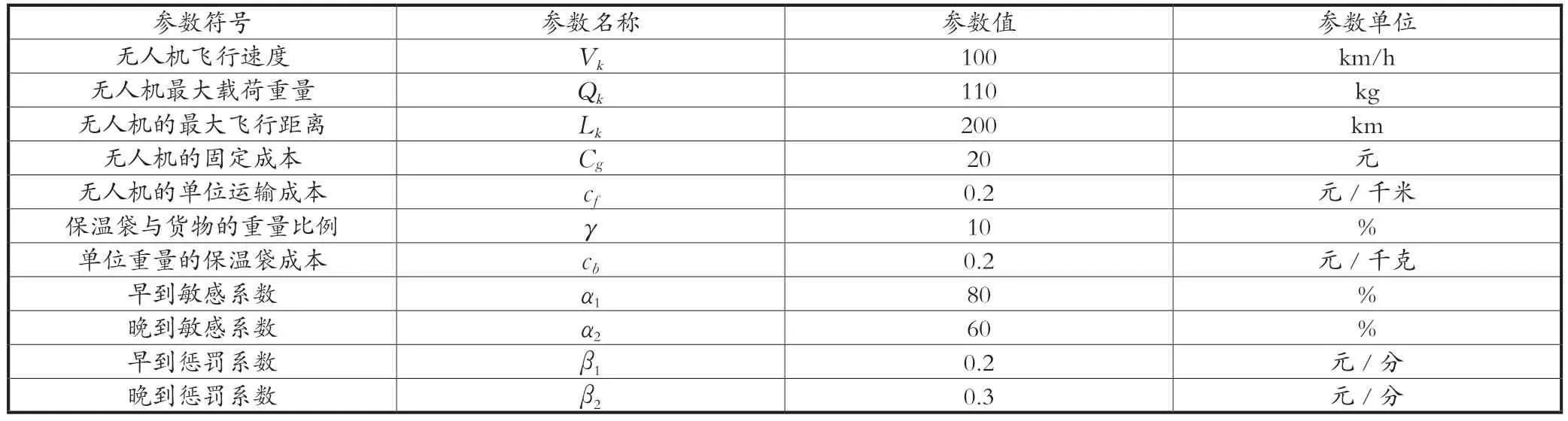
表1 相关参数设置
4.2 算例仿真结果
本文分别采用了模拟退火算法、自适应大邻域搜索算法及混合遗传算法进行实验运算。在参数相同的情况下,本文在Windows 10系统、16GB内存、AMD Ryzen 5 5600H with Radeon Graphics的处理器上采用PYTHON进行无人机配送路径的仿真实验。混合遗传算法的路径示意图如图1所示。其中,红色圆形区域代表绕行或等待的限飞区,绿色圆点代表客户点的位置。
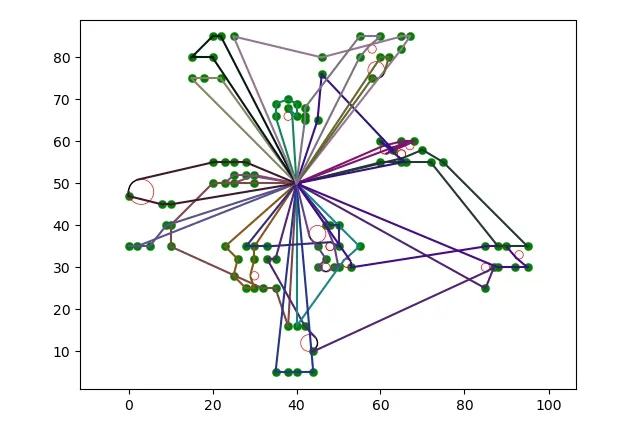
图1 路径示意图
算法运行的结果对比如表2所示。

表2 算法结果对比
从表2可以看出,与自适应大邻域搜索算法及模拟退火算法相比,混合遗传算法的总客户满意度数值分别提高了5.39%及5.65%,总成本下降了28.96元及0.2元。因此,本文所采用的混合遗传算法与传统算法相比,可以在耗费较低配送成本的同时取得较高的客户满意度。
5 结 论
本文讨论了无人机在两个客户点之间至多存在两个限飞区的飞行限制情况下,综合考虑客户满意度及配送成本的生鲜产品配送路径优化问题。本研究考虑无人机在限飞区内的飞行时间与限飞区本身的限飞时间重叠的情况下,无人机可根据配送成本选择等待或绕道飞行限飞区,并对现有研究中的绕行路径进行了优化。本文将自适应大邻域搜索算法与模拟退火算法及遗传算法相结合,大幅提升了编码的多样性,扩大了算法在解空间的搜索范围,进一步提高算法找到更优解的概率。最后PYTHON仿真实验表明,本文所设计的混合遗传算法有效提高了全局搜索能力,取得了较传统算法更优的解,且迭代次数较少。此外,研究仅仅考虑了限飞区对于无人机产生的飞行限制,未来可进一步考虑更多飞行限制情况对无人机物流配送的影响等。

