一种基于敏感因子加权的机构动力学仿真方法

于婷婷 连华东 杨柳 赵鑫 梁凤超 范建凯 林喆

一种基于敏感因子加权的机构动力学仿真方法

于婷婷 连华东 杨柳 赵鑫 梁凤超 范建凯 林喆

（北京空间机电研究所，北京 100094）

为了解决批产高精度调焦机构有限元分析与扫频试验结果存在偏差的问题，提高空间复杂机构设计能力，文章提出了一种基于敏感因子加权系数的机构动力学有限元分析法。该方法基于Hertzian接触理论建立了运动副连接的等效刚度模型，确定了敏感因子及其刚度贡献的关键方向，根据刚度与基频关系以及相关试验数据，为模型中敏感因子分配了加权系数，实现了机构的高精度仿真。利用该仿真方法对某空间相机高精度调焦机构进行仿真分析，并与扫频试验进行对比，结果表明前三阶基频振动特性一致且误差均小于2.8%，验证了该方法的有效性和计算效率，可为高精度空间机构的仿真分析提供一定参考。

空间机构 刚度 加权 有限元分析 振动特性 空间相机

0 引言

空间光学相机在轨工作寿命期内，由于发射阶段过载冲击、在轨环境温度变化等因素的影响，会产生离焦从而影响成像品质。调焦机构作为当前空间相机中重要组成部分之一[1]，能够校正偏离的焦面，使相机的光学性能满足成像要求。目前调焦机构通常采用固体润滑角接触球轴承实现结构支撑，利用步进电机进行驱动，并通过滚珠丝杠副及导轨滑块组件实现定位导向。由于机构连接部组件复杂，运动副连接中存在间隙、摩擦等现象，且预紧力直接影响刚度的变化，导致活动机构在有限元分析时，不能像对简单结构件仿真一样逐一处理接触应力或等效刚度等，如此造成活动机构的有限元分析工作量巨大、程序运算慢，甚至计算出的结果与实际力学特性差距很大，不能为机构的设计迭代提供指导。尤其空间相机中的机构负载均是光学元件，机构有限元分析的不准确则不能为光学元件提供有力保障。因此，如何高效准确的模拟预测机构刚度特别是运动副连接刚度，并快速准确的进行有限元处理，对于高精度空间运动机构的设计与力学特性分析具有重要意义。

针对复杂机构刚度的分析方法已开展了许多相关研究，如Gosselin C[2]建立了并联机构工作空间内的刚度映射和条件数映；赵铁石等[3]基于影响系数法，并借助虚功原理，建立了包含弹性变形及刚度连续变化过程的并联机构连续刚度非线性映射通用模型；李嘉等[4]利用有限元技术，针对两类移动副和一类球副的不同结构组合，分析了结构参数对其刚度性能的影响。上述研究从理论方面扩展了刚度模型的分析方法，其中许多研究针对刚度模型采用了大量的分析计算及复杂的有限元分析手段。但在工程实践中，特别是针对高精度、部组件连接关系复杂的空间精密机构，高效准确完成优化模型的设计，以简单的方式建立连接副刚度的近似模型，并给出可靠准确的仿真结果，具有重要的工程意义。

本文针对光学遥感相机中一维直线调焦机构的动力学特性开展了有限元分析研究，通过判断刚度模型敏感因子，分析敏感因子的主要贡献刚度方向，并采用加权系数分配法[5-6]将不敏感因子的刚度贡献等效至敏感因子刚度，将复杂机构的刚度模型简单化，基于刚度参数创建仿真连接关系，提高了仿真模型的准确性；最后通过试验对仿真模型进行了验证，结果表明增加权系数后的仿真结果精度大大提高。该方法提高了复杂活动机构设计迭代优化的效率，高效准确的仿真结果为后续试验验证奠定了有力基础，可应用于同类传动方式的运动机构的设计与动力学特性研究。

1 机构敏感因子刚度分析

刚度是影响机构动态性能的重要评价指标，本文以某空间遥感相机中的调焦机构为例，基于对机构运动副的刚度分析，开展了对机构的有限元分析研究。如图1所示，调焦机构由步进电机通过减速齿轮副驱动精密微型滚珠丝杠实现旋转变直线运动，其中滚珠丝杠副主要承受机构运动方向的轴向力；丝杠两端使用面对面安装角接触球轴承支撑并轴向定位预紧，增加机构轴向承载力；为实现高精度一维导向运动，机构中采用了一对可承受法向载荷的HSR导轨滑块组件。

根据对相同构型机构的试验数据整理发现，前3阶扫频试验的运动方向均相同，分别表现在机构的轴向、径向和法向（即图1中的、、方向），且关键因子刚度的变化直接线性影响机构的前3阶基频。调焦机构中主要通过滚珠丝杠副和轴承承受向载荷，导轨滑块组件和轴承同时承受向载荷，但导轨滑块主要承受向载荷，因此可以确定在、、三个方向主要贡献刚度的因子为滚珠丝杠副、轴承和导轨滑块副，并分析出了3个敏感因子的主要贡献方向。由于活动机构在不同状态下的刚度变现不同，研究方法为了保证机构状态一致，机构力学试验模拟发射过程进行了位置锁定，此时可认为机构刚度保持不变。

在机构的有限元分析中，调焦机构在、、向的刚度K、K、K是关键指标，直接影响机构力学试验结果。其中，K主要取决于滚珠丝杠副及角接触球轴承系统的刚度，K取决于导轨滑块及角接触球轴承系统的刚度，K取决于导轨滑块系统的刚度。因此基于Hertzian接触理论[5-6]，在假定材料均匀、各向同性且完全弹性，以及接触表面的摩擦力忽略不计的条件下，结合机构中敏感因子的各方向刚度的串并联关系，并忽略结构主体结构刚度影响，可近似得出调焦机构在、、向的刚度K、K、K为

式中 K11为轴系滚珠丝杠副轴向刚度；K21为轴承轴向刚度；K22为轴承径向刚度；K23为轴承法向刚度；K32为导轨滑块径向刚度；K33为导轨滑块法向刚度；ζ11为滚珠丝杠副刚度权系数；ζ21为轴承轴向刚度权系数；ζ22为轴承径向刚度权系数；ζ32为导轨滑块径向刚度权系数；ζ33为导轨滑块法向刚度权系数。系统刚度模拟如图2所示。

图2 系统刚度模拟示意

对系统各敏感因子进行刚度分析计算时，虽然忽略了其他结构件的刚度，但为提高系统刚度模型的计算精度、保证仿真的准确性，需将不敏感因素对系统力学特性的影响，通过刚度参数拟合到敏感因子权系数中；确定敏感因子后，对3个敏感因子关键方向的刚度展开求解及权系数计算。由于敏感因子结构内均包含滚珠，刚度计算复杂，因此在依据Hertzian接触理论的基础上还参考了近年较为准确而简便的算法[6-7]。

1.1 滚珠丝杠副刚度

调焦机构中承载轴向载荷的活动副包含滚珠丝杠副与轴承，其中滚珠丝杠副的预紧方式一般有3种：双螺母垫片预紧（通过改变两螺母间垫片厚度调整预紧力）、单螺母变位导程预紧（通过在导珠管之间改变某一导程施加预紧）、单螺母增大钢球预紧（通过大直径钢球调整预紧）。图3为滚珠丝杠副综合性能退化曲线，可以看出：预紧力越大，接触刚度增加，定位精度高，伴随寿命降低。因此在调焦机构关键运动副设计中，综合考虑产品力学性能和服役寿命要求，保证钢球固体润滑MoS2膜层的寿命，设计滚珠与滚道存在5 μm间隙，理论是无预紧状态，但实际装配后，由于滚道与钢球存在尺寸偏差，会出现微预紧力，存在图4所示的2点式接触。

图3 滚珠丝杠副综合性能退化曲线示意

图4 钢球预紧方向示意

根据滚珠丝杠副在机构中的安装方式及受力方式，轴向刚度11主要由滚珠丝杠轴向刚度S、滚珠螺母轴向刚度N、螺母及轴承安装基座轴向刚度H三方面组成[7]。

1）滚珠丝杠轴向刚度S与安装方式有关，本文调焦机构采用固定-固定的安装方式，因此，在刚度计算过程中必须考虑丝杠螺母到固定支撑点产生的最大轴向位移，S为[7]

式中为以丝杠螺纹滚道底径为直径的横截面积（mm2）；为弹性模量（MPa）；为两端支撑轴承间距（mm）；为丝杠螺母至固定点间距（mm），当/2时产生最大轴向位移。

2）钢球与螺纹滚道在2点式接触过程中会产生弹性和塑性变形，在钢球与滚道面承受最大接触应力处，只产生1/10 000钢球直径的塑性变形，所以仅分析接触面发生弹性变形条件下的刚度[7]，即

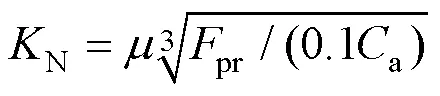
式中为行程范围内根据精度等级确定的行程变动量系数，取值范围为[0.5,0.6]；pr为丝杠副的预紧力（N·m）；a为额定动载荷（N）。

3）考虑滚珠丝杠副及支撑轴承安装基座的轴向刚度，可按照结构件单轴方向受载计算H，即

式中为支撑基座轴向方向承受的载荷。

综合上述因素，可以得到敏感因子滚珠丝杠副的轴向刚度11为[7]

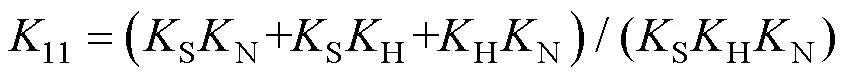
根据式（5），并结合式（2）～（4）及滚珠丝杠副手册中相关参数，可求得轴向接触刚度11=851.32 N/μm。由于机构设计过程中，滚珠丝杠副两端通过一组面对面角接触球轴承支撑，并通过一组卸载径向力装置与活动板连接，已经最大限度避免了滚珠螺母承受径向载荷或扭矩载荷的情况，故这里忽略径向、法向刚度12和13。

1.2 轴承刚度

调焦机构中滚珠丝杠副两端采用了面对面方式的角接触球轴承，如图5所示通过预紧端盖压紧轴承外圈，由于实际装配过程需在安装一端轴承端盖后，才可以对另一端进行预紧，施加轴向力a使内圈压紧，轴承内外圈产生不等的相对位移a，两端预紧力转变为a1、a2，此时轴向预紧力a可表示为[8]

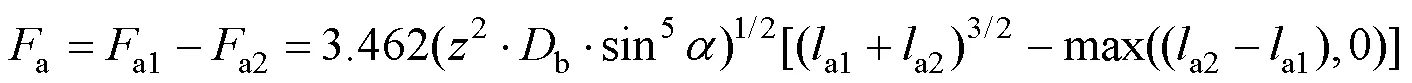
式中b为角接触球轴承滚珠直径（mm）；为角接触球轴承给接触角（°）；a1a2分别为未预紧与预紧端轴承内外圈位移量（mm）；为钢球数量。

通过轴向位移与轴向力的关系，可计算出轴向刚度21，即

在施加预紧力初始阶段，轴承刚度与预紧力呈正比，与寿命呈反比关系（如图6所示）；之后伴随预紧力的增大，刚度逐渐增大，而寿命逐渐减小，当预紧力到达临界点时，轴承刚度趋于稳定值，寿命加剧减小。

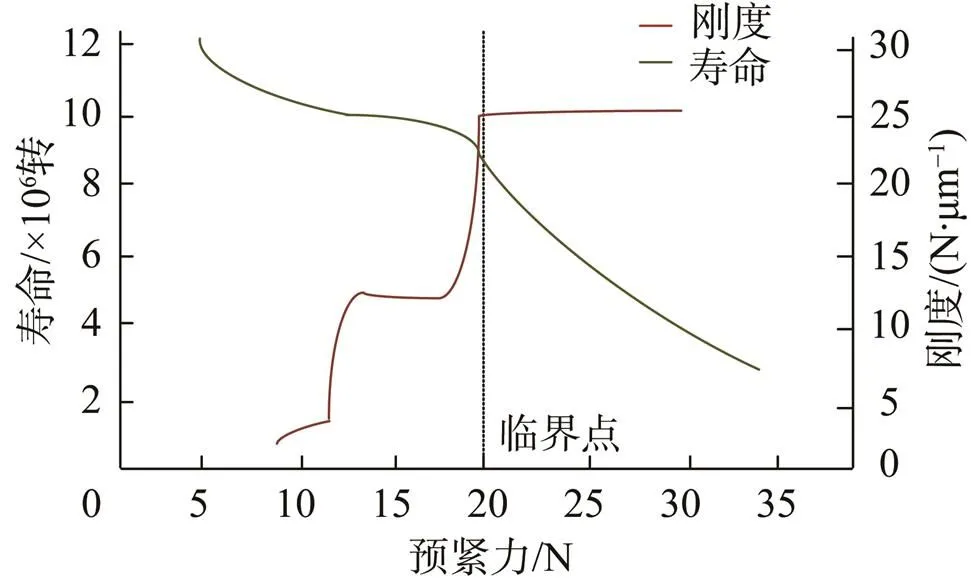
图6 轴承预紧后参数变化关系

对于轴向预紧作用下轴承的刚度，已有许多简便算法，针对角接触球轴承的轴向刚度21及径向刚度22，本文参考文献[8-11]进行计算，将轴向预紧力看作施加轴向载荷a，从而在轴承内外圈产生相对位移a，得到21及22的近似值：

调焦机构中使用的角接触球轴承为708C轴承，为满足刚度与寿命的要求，采用定压预紧的方式施加小预紧力，对708C轴承单个轴承施加轴向载荷进行计算，通过预紧增大摩擦力矩（2～3）×10–3N∙m，保证轴承刚度约为 988.7 N/μm。对于径向刚度22，在后续计算中减少变量，因此假定22保持不变。由于机构中轴承支撑于滚珠丝杠副两端，且滚珠丝杠副与负载间存在间隙无法承载法向力，因此分析中可以忽略轴承法向刚度23。

1.3 导轨滑块刚度

导轨在调焦机构中主要承载径向载荷，可以忽略轴向刚度31。当导轨副承受径向和法向载荷时， 4列滚道中任一钢球都与导轨、滑块形成接触副，具体受力情况如图7所示。调焦机构中支撑负载的径向刚度与法向刚度主要取决于导轨的结构参数和滚珠的弹性变形。在负载水平匀速运动过程中，滑块与导轨在容许载荷范围内产生弹性变形，此时产生的径向载荷与变形量之比即为径向刚度。

图7 受径向载荷时导轨滑块副受力示意

进行导轨滑块刚度分析时，将导轨外滚道、滑块内滚道与钢球的局部接触区域均视为弹性体，载荷作用在一个小的椭圆形区域，从而产生局部弹性变形。依据THK导轨技术手册提供的关键参数[12-16]，计算导轨滑块组件的径向刚度32与法向刚度33[17]，具体公式为

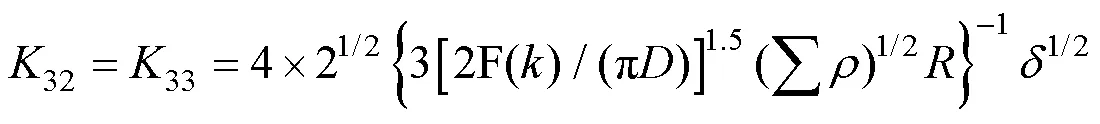
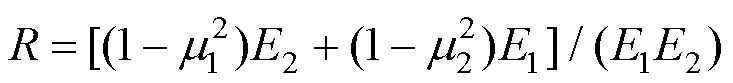
调焦机构应用的HSR12导轨滑块副包含4列滚动面，各钢球列接触角均为45°，拟定在径向与法向具有相同的额定载荷。根据导轨参数，通过式（9）可计算出导轨单个滚珠在径向与法向的刚度，32=33=899×104N/μm。

2 敏感因子加权系数分配

加权分配法考虑到各分系统对整个系统的影响程度，以分系统刚度引起整个系统刚度特性发生变化的概率为依据，来计算各影响因子权系数。章节1中已获得3个敏感因子关键方向的刚度，基于大量相同构型机构的历史试验数据，可计算各因子权系数。但考虑到机构是由多个结构件和高精度运动副装配组成，权系数不仅评价因子的敏感程度，还需要考虑其他不敏感因素的影响刚度，因此本文在采用加权分配法的同时，也将不敏感因子刚度的影响综合到了权系数中，保证整体刚度接近实际值。

由于式（1）中未知权系数大于求解方程数，因此先根据机构3个方向的刚度特性确定3个权系数。其中滚珠丝杠副只承受轴向载荷，其轴向刚度值在实际中装配易于控制，误差范围较小，因此定义权系数11=1；轴承通过预紧来增加轴向刚度，对于刚度K、K，轴承对整体结构的径向刚度影响小，因此可以假定权系数22=1。

因此，对于、、三个方向的不敏感因素刚度误差，将其中的轴向刚度误差等效至系数21，径向刚度误差等效至系数32，法向（向）误差等效至系数33。

相同构型的调焦机构具有相同的敏感因子。根据基频与刚度影响呈线性关系的条件，对相同构型机构的扫频试验结果及仿真结果进行对比计算，可以获得K、K、K，将这3个数值和之前计算出的敏感因子刚度值及系数11、22、23等一并代入式（1），求解出21、32、33。经计算，21=1.05，32=1.2，33=1.33。利用上述结果，可得到分配权系数后的敏感因子刚度模型。

3 仿真与试验验证

通过分析敏感因子对机构刚度的影响，获得各组件刚度信息，在此基础上建立调焦机构有限元仿真模型，并对机构敏感因子刚度的准确性进行验证，为后续加权系数的确定提供可靠数据。考虑到机构中细节特征复杂、异形结构件较多，几何建模过程中需要花费较多时间进行几何清理和网格划分，为了快速准确发现模型问题及优化模型，本文通过Ansys Workbench建立机构仿真模型，实现针对复杂机械系统的快速仿真验证。在仿真验证过程中，首先利用Workbench自动创建的刚性连接模型得到仿真结果，由于该结果并不完全符合直线机构力学特性规律，因此初始模型不够准确，证明机构内活动部件设置模拟连接副的重要性；通过对敏感因子设置模拟连接副，建立准确的仿真模型，并对有无加权系数的情况进行仿真；最后与试验结果进行对比分析，验证增加权系数的意义。仿真分析时涉及的结构材料属性如表1所示。为了将仿真误差降到最低，仿真模型中将网格的精细程度以及单元阶数的设置，选择10节点四面体单元，保证分析结果符合收敛性要求。

表1 结构件材料

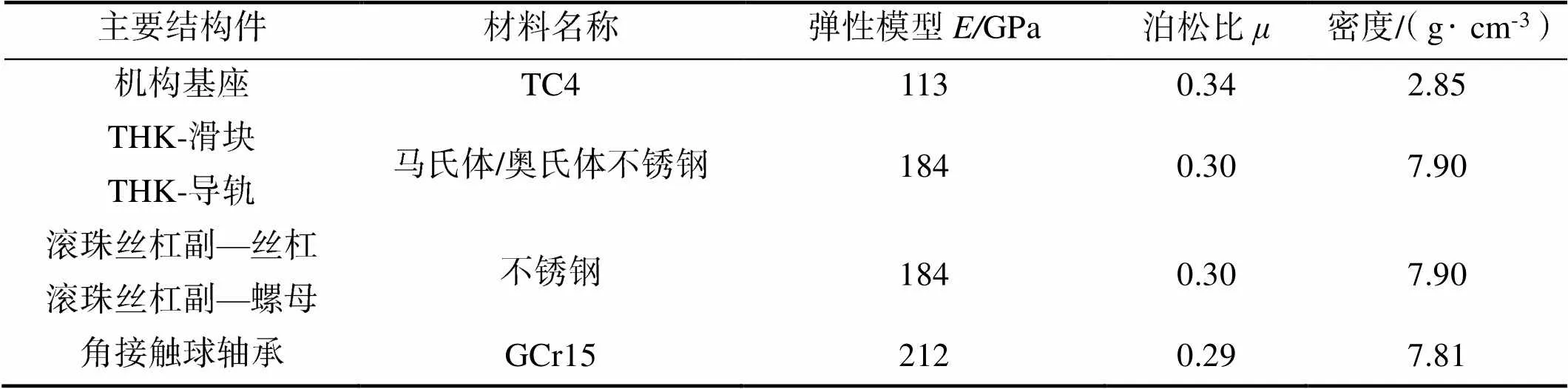
Tab.1 Material properties

3.1 仿真模型的建立与优化

根据一维直线运动机构的力学特性可知，机构的第一阶基频表现为向的位移运动，原因是由于机构沿向一维运动，向刚度主要依靠轴承与滚珠丝杠副的轴向刚度；第二阶基频表现为法向方向的运动；第三阶基频表现为径向方向的运动。通过该规律初步验证仿真模型的准确性。

首先，通过Workbench中自动创建的刚性连接关系进行简单仿真，验证自动生成连接关系的仿真模型是否准确，初始仿真结果如图8所示。结果表明：第一阶频率发生在机构与负载连接的柔性卸载节处；第二阶频率发生在柔性卸载节中连接杆上，表现为负载的向平移；由于整体结构中悬臂结构的特性，在第三阶频率出现了机构整体绕向的旋转运动。上述仿真结果中，最明显的一阶基频并不是沿向的平动，与力学特性规律存在明显差别，因此该仿真模型通过刚性连接的方法误差太大，需要根据运动副刚度及其连接关系，对模型中各部件连接方式进行修改完善。

图8 初始仿真结果

综合上述分析，采用模拟运动副方法，用弹簧单元来模拟连接刚度，创建更为准确的连接关系。3个敏感因子的模拟连接关系如下。

1）滚珠丝杠副：滚珠丝杠副螺杆的转动变为螺母的平动，在仿真模型中，放开螺母与螺杆轴向转动和轴向平移自由度，并施加轴向刚度约束11。

2）轴承：由于电机驱动齿轮副带动丝杠轴旋转，轴承内圈相对外圈旋转，在模型中释放轴承与基座之间轴向转动和平动约束，分别在向施加刚度21，在径向施加刚度22，模拟轴承的连接刚度。

3）导轨滑块组件：作为机构中支撑和导向部件，导轨滑块组件刚度主要影响径向和法向基频。在模型中连接关系设置为：释放方向平动自由度，并在向和向分别施加刚度32和33。

在建立了模拟连接副并设置敏感因子的刚度11、21、22、32和33后求解，仿真结果如图9所示，为更直观的判断机构模态仿真结果的运动方向，图9中将负载与活动板隐藏。

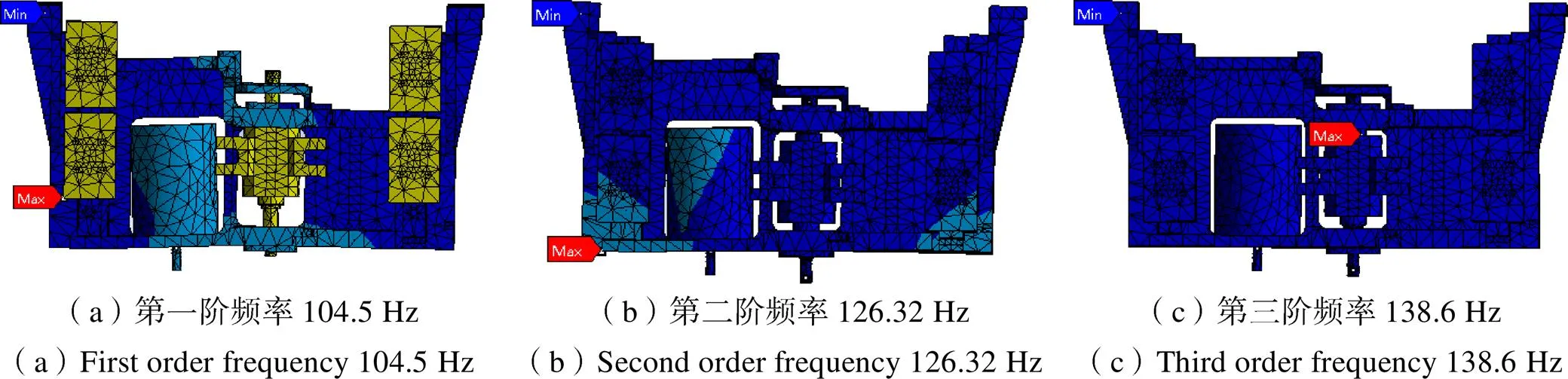
图9 建立连接副后的仿真结果（无加权系数）

可以看出，第一阶频率为104.5 Hz，运动表现为活动部件（活动板、滑块及丝杠螺母）沿向平动；第二阶频率为126.32 Hz，运动表现为机构整体沿向的摆动；第三阶频率为138.6 Hz，运动表现为机构整体在向摆动。前3阶机构频率特性与一维直线机构的力学特性规律一致，因此可确认仿真模型建立正确，同时也获得了无加权系数情况下的仿真结果。在该仿真模型基础上进行权系数分配，保证后续提高基频分析精度。

3.2 分配加权系数后的仿真

基于准确的机构仿真模型，对模拟连接副中的刚度值依次分配加权系数后，再次进行仿真分析验证，验证敏感因子刚度值分配权系数的必要性。由图10可以看到，第一阶频率为115.88 Hz，运动表现为运动部件（活动板、滑块及丝杠螺母）的向平动；第二阶频率为139.6 Hz，机构整体向摆动；第三阶频率为143.8 Hz，机构整体表现为向摆动。各阶运动方向依旧与力学特性规律一致。。

图10 分配加权系数后的仿真结果

3.3 扫频试验验证

为了验证模拟连接副配合权系数仿真方法的精度，对机构进行了动力学试验，图11中给出了、、三个方向的扫频试验结果，以及关键测点的频率响应曲线，可以看到3个方向的基频分别为116.2、142.5、147.9 Hz，试验结果与同构型一维直线机构的力学特性规律保持一致，且曲线中频率点未出现断崖式下跌，说明机构中各组件不存在异常情况，试验结果可靠。表2给出了试验结果与有无加权系数模态仿真结果的对比。可以看出，在考虑了连接刚度的加权系数后，得到的仿真结果与试验结果误差最大不超过2.8%，而无加权系数仅考虑连接刚度时的误差最小为6%，最大可至10%。因此，通过分配准确的连接刚度加权系数，在此基础上进行机构仿真计算，可以大大提高机构的仿真精度，为后续机构设计中提高基频、保护负载起到了重要作用。

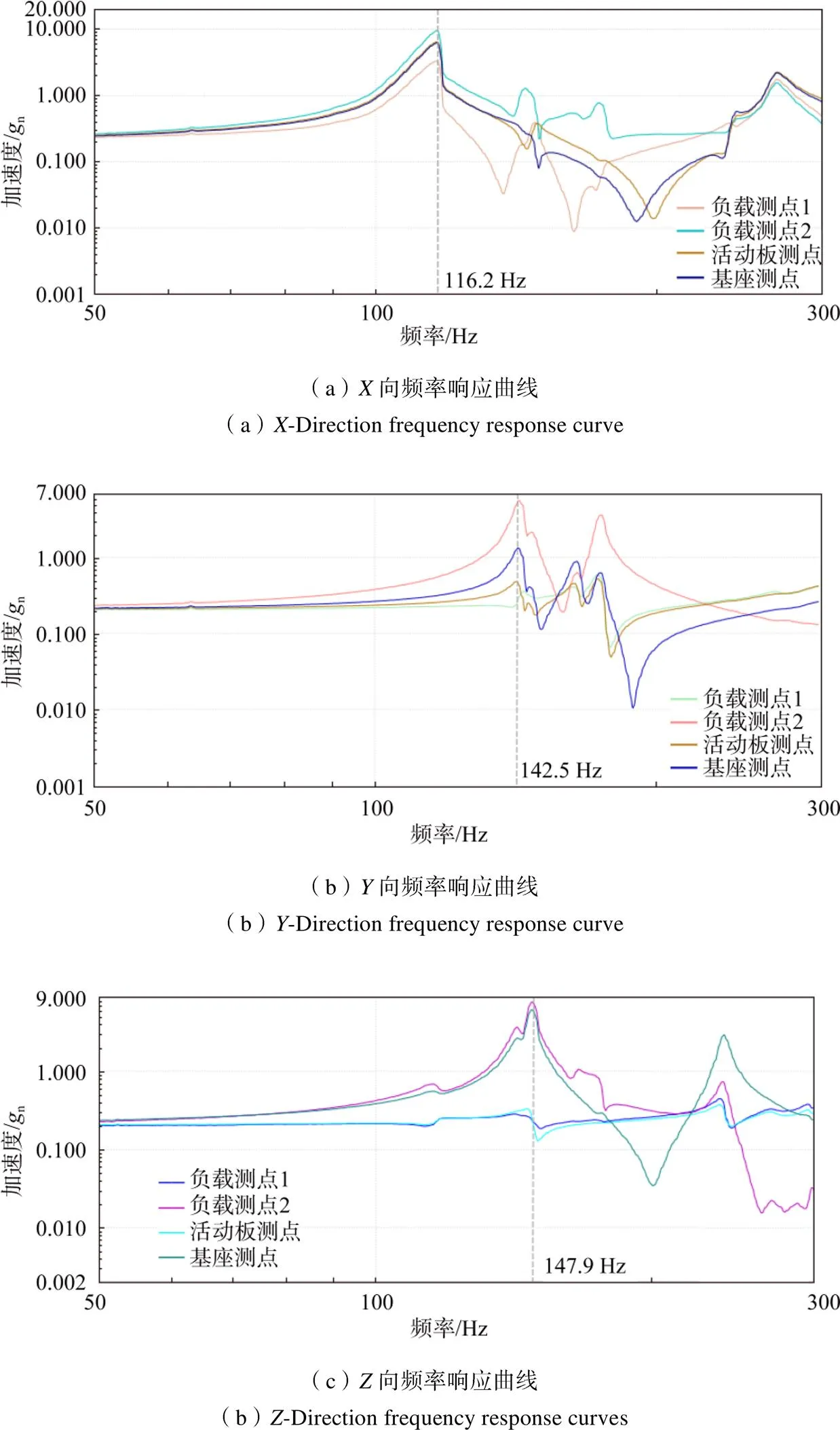
图11 频率响应曲线

表2 仿真与试验结果对比验证结果

Tab.2 Comparison between simulation and test results

4 结束语

针对批产调焦机构仿真结果偏差较大问题，为了提高动力学特别是频率仿真精度，以便为设计改进和力学试验提供有力参考，本文利用Hertzian接触理论在对接触区域弹性分析的基础上，分析了滚珠丝杠副、角接触球轴承及导轨滑块等运动副在3个不同方向的刚度。根据同类构型调焦产品试验结果和仿真数据，确定了仿真模型中不同连接刚度所需的加权系数。考虑了连接刚度加权系数后，仿真精度大大提高，与试验结果误差最大不超过2.8%。该仿真方法深度剖析了一维运动机构各部组件的连接关系及对整体的刚度贡献值，提高了复杂活动机构的设计与仿真验证的效率与准确性，可应用于同类传动方式的运动机构的设计与动力学特性研究。

[1] 谭伟, 王殿中, 何红艳, 等. “高分七号”卫星相机高精度快速在轨调焦方法[J]. 航天返回与遥感, 2020, 41(2): 78-86. TAN Wei, WANG Dianzhong, HE Hongyan, et al. Reserch on High Accurate Refocusing Method of GF-7 Camera[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(2): 78-86. (in Chinese)

[2] GOSSELIN C. Stiffness Mapping for Parallel Manipulators[J]. IEEE Transactions on Robotics and Automation, 1990, 6(3): 337-382.

[3] 赵铁石, 赵延治, 边辉, 等. 空间并联机构连续刚度非线性映射[J]. 机械工程学报, 2008, 44(8): 20-25, 32. ZHAO Tieshi, ZHAO Yanzhi, BIAN Hui, et al. Continuous Stiffness Nonlinear Mapping of Spatial Parallel Mechanism[J]. Chinese Journal of Mechanical Engineering, 2008, 44(8): 20-25, 32. (in Chinese)

[4] 李嘉, 陈恳, 董怡, 等. 并联柔性铰机器人的静刚度研究[J]. 清华大学学报(自然科学报), 1999, 39(8): 16-20. LI Jia, CHEN Ken, DONG Yi, et al. Study on the Static Stiffness of the Parallel Flexure Joint Robot[J]. Journal of Tsinghua University(Science & Technology), 1999, 39(8): 16-20. (in Chinese)

[5] 王乐, 李冬, 余慕春, 等. 基于动态加权系数和多目标进化的模型修正方法[J]. 振动与冲击, 2020, 39(4): 284-290. WANG Le, LI Dong, YU Muchun, et al. A Method of Model Updating Based on Dynamic Weighting Coefficients and Multi-Objective Evolution[J]. Journal of Vibration and Shock, 2020, 39(4): 284-290. (in Chinese)

[6] 程鹏辉, 吴萌源. 空间相机调焦平台的动力学特性研究[J]. 光学精密工程, 2019, 27(3): 602-609. CHENG Penghui, WU Mengyuan. Research on Dynamic Characteristics of Space Camera Focusing Platform[J]. Optics and Precision Engineering, 2019, 27(3): 602-609. (in Chinese)

[7] JCSGY精密滚珠丝杠副手册[M]. 北京: 北京工研精机股份有限公司, 2008. JCSGY BALL SCREWS[M]. Beijing: Beijing Precision Mechinery & Research CO. LTD. (in Chinese)

[8] 李为民, 王海涛. 轴向定位预紧轴承刚度计算[J]. 河北工业大学学报, 2001, 30(2): 15-19. LI Weimin, WANG Haitao. Rigidity Calculation of Axial Position Preload Bearings[J]. Journal of Hebei University of Technology, 2001, 30(2): 15-19. (in Chinese)

[9] GUNDUZ A, DREYER J T, SINGH R. Effect of Bearing Preloads on the Modal Characteristics of Ashaft-Bearing Assembly: Experiments on Double Row Angular Contact Ball Bearings[J]. Mechanical Systems and Signal Processing, 2012, 31: 176-195.

[10] OZTURK E, KUMAR U, TURNER S, et al. Investigation of Spindle Bearing Preload on Dynamics and Stability Limit in Milling[J]. CIRP Annals-Manufacturing Technology, 2012, 61(1): 343-346.

[11] 杨静文. 端盖螺栓拧紧工艺对轴承预紧载荷影响研究[D]. 大连: 大连理工大学, 2018. YANG Jingwen. Research on Influence of Tightening Technology of Bearing Cap’s Bolts on Bearing Preload[D]. Dalian: Dalian University of Technology, 2018. (in Chinese)

[12] THK公司. THK综合产品目录<直线运动系统>-B产品尺寸规格[M]. [出版地不详]: THK公司, 2017. THK CO, LTD.T HK Catalog No．511C-B Product Specifications[M]. [S.l.]:THK CO, LTD., 2017. (in Chinese)

[13] YI Y S, KIM Y Y, CHOI J S, et al. Dynamic Analysis of a Linear Motion Guide Having Rolling Elements for Precision Positioning Devices[J]. Mechanical Science and Technology, 2008, 22(1): 50-60.

[14] KATO S, IGARASHI Y. Effects of Ball Groupings on Ball Passage Vibrations of a Linear Guideway Type Ball Bearing, Pitching and Yawing Ball Passage Vibrations[J]. Journal of Tribology, 2007, 129(1): 188-193.

[15] 宁星超. 滚动直线导轨动态特性研究[D]. 大连: 大连理工大学, 2016. NING Xingchao. Study on the Dynami Characteristics of Rolling Linear Guide[D]. Dalian: Dalian University of Technology, 2016. (in Chinese)

[16] 安源, 杜一民, 贾学志, 等. 空间相机调焦机构自锁特性评价与试验[J]. 光学精密工程, 2018, 26(2): 355-362. AN Yuan, DU Yimin, JIA Xuezhi, et al. Evalution and Test of Self-Locking Ability for Focusing Mechanism of Space Camera[J]. Optics and Precision Engineering, 2018, 26(2): 355-362. (in Chinese)

[17] 田洪亮, 郑金华, 陈甜敏, 等. 直线运动滚动导轨副的法向接触力学模型[J]. 西安交通大学学报, 2016, 50(5): 1-11. TIAN Hongliang, ZHENG Jinhua, CHEN Tianmin, et al. Normal Contact Mechanics Model of Linear Motion Rolling Guideway Pair[J]. Journal of Xi’an Jiaotong University, 2016, 50(5): 1-11. (in Chinese)

[18] 吕帮俊, 朱石坚, 彭利坤, 等. Stewart机构刚度映射建模与仿真[J]. 振动与冲击, 2011, 30(4): 178-181. LU Bangjun, ZHU Shijian, PENG Likun, et al. Stiffness Mapping Modeling and Simulation for Stewart MechaIlism[J]. Journal of Vibration and Shock, 2011, 30(4): 178-181. (in Chinese)

[19] 马雅丽, 宁星超, 钱峰, 等. 滚动直线导轨固有特性分析[J]. 华中科技大学学报: 自然科学版, 2016, 44(9): 59-64. MA Yali, NING Xingchao, QIAN Feng, et al. Natural Vibration Performance Analysis of Rolling Lineat Guide[J]. Journal of Huazhong University of Science &Technology: Natural Science Edition, 2016, 44(9): 59-64. (in Chinese)

[20] 孙伟, 鲁明, 汪博, 等. 直线滚动导轨动力学特性分析方法研究[J]. 制造技术与机床, 2011(3): 48-53. SUN Wei, LU Ming, WANG Bo, et al. Research on Analysis Method of Dynamics Characteristics for Linearrolling Guide[J]. Manufacturing Technology＆Machine Tool, 2011(3): 48-53. (in Chinese)

[21] 李建栋, 朱永生, 熊青青, 等. 定压预紧主轴轴向动态刚度特性研究[J]. 西安交通大学学报, 2014, 48(10): 126-130. LI Jiandong, ZHU Yongsheng, XIONG Qingqing, et al. Research on Axial Dynamic Stiffness of Fix-Pressure Spindle[J]. Journal of Xi'an Jiaotong University, 2014, 48(10): 126-130. (in Chinese)

[22] 陈星星. 具有零刚度特性的常力微动平台设计、建模与性能分析[D]. 赣州: 江西理工大学, 2018. CHEN Xingxing. Design, Modeling and Performance Analysis of Constant-Force Stage with Zero Stiffness[D].Ganzhou: Jiangxi University of Science and Technology, 2018.

[23] 尹航. 冗余轮辐式六维力感知机构刚度建模理论与仿真分析[D]. 秦皇岛: 燕山大学, 2020. YIN Hang. The Theory and Simulation Analysis of Stiffness Modeling of Redundant Spoke SIX-Dimensional Force Sensing Mechanism[D]. Qinhuangdao: Yanshan University, 2020. (in Chinese)

A Simulation Method of the Dynamic Characteristics for Space Optical Mechanisms Based on Weighted Factors

YU Tingting LIAN Huadong YANG Liu ZHAO Xin LIANG Fengchao FAN Jiankai LIN Zhe

（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

To reduce of the deviation between analysis and test results and improve the design performance for space complex mechanisms, a dynamic finite element analysis method for space focus adjustment mechanisms is proposed based on sensitive factor weighted coefficients. This method establishes an equivalent stiffness model of the motion pair joints based on the Hertzian contact theory, and clarifies the key direction of the sensitive factor and its stiffness contribution. According to the relationship between stiffness, the fundamental frequency and relevant test data, the weighted coefficients of the sensitive factors in the model are determined, thus achieving high-precision simulation. Using this simulation method, the performance of a high-precision focus adjuststment mechanism in a space camera is analyzed with and without weighted coefficients, and the results are compared with the sweep test ones. The comparisons show that for the first three fundamental frequencies, the vibration characteristics are consistent and the fundamental frequency error is less than 2.8%, verifying the effectiveness of the method and providing a reference for the simulation analysis of high-precision space mechanisms.

space mechanism; stiffness; weighted; finite element analysis; vibration characteristics; space camera

V423.9

A

1009-8518(2023)03-0051-11

10.3969/j.issn.1009-8518.2023.03.006

于婷婷，女，1994年生，2020年获北华航天工业学院航天工程专业硕士学位，助理工程师。主要研究方向为空间光学遥感机构。E-mail：Yutt1994ting@163.com。

2022-10-20

国家自然科学基金（62227812）

于婷婷, 连华东, 杨柳, 等. 基于敏感因子加权的机构动力学仿真方法[J]. 航天返回与遥感, 2023, 44(3): 51-61.

YU Tingting, LIAN Huadong, YANG Liu, et al. A Simulation Method of the Dynamic Characteristics for Space Optical Mechanisms Based on Weighted Factors[J]. Spacecraft Recovery & Remote Sensing, 2023, 44(3): 51-61. (in Chinese)

（编辑：夏淑密）