基于生成对抗网络的小样本颜色空间转换方法
林松,孙连山,赵娟宁,吴彦锦
(陕西科技大学 电子信息与人工智能学院,西安 710021)
在早期的图像显示领域,由于设备制造标准、制造厂商、运行环境的不同,造成不同设备的显示能力有所差异,因此同一张数字图像在不同设备上直接显示或输出就会产生肉眼可见的色差。为了降低图像在不同设备之间的色差,国际色彩协会于1995 年提出色彩管理[1-2]标准,自此,色彩管理系统就成为图像显示领域必不可少的部分。
色彩管理的本质是颜色值在颜色空间之间的转换,颜色空间是一种用于描述色彩的方式,不同颜色空间只是对同一物理量的描述方式不同,相互之间存在转换关系,常见的标准颜色空间有RGB、CIELab、XYZ 等。在实际应用中,由于设备老化等各种原因,标准颜色空间的转换关系无法直接应用于色彩管理,需要根据设备的特点创建设备特有的非标准颜色空间转换关系。记录设备颜色空间转换关系的文件称为设备特性化文件。色彩管理需要根据特性化文件在不同颜色空间之间转换同一张图像,转换的精度直接影响色彩管理系统的色差。长期以来,许多学者致力于研究整体性能优秀的颜色空间转换方法,主流方法有3 类:三维查找表法、多项式回归法和神经网络模型法[3]。
在传统方法中,基于三维查找表法[4-5]的转换方法采用均匀空间的距离公式来计算色域空间上的颜色距离,所以中间点的转换精度受到查找表的限制。为查找表引入新的数据点是十分烦琐的过程,需要重新计算大部分坐标点,因此这种方法的使用频率逐渐下降。基于多项式回归[6-7]的转换方法在确定回归阶数和常数项时存在不确定性,随着阶数的增加,计算量逐渐增大,模型更复杂。
在神经网络模型法中,杨金锴等[3]为极限学习机的目标函数引入正则化项,再根据岭回归模型的岭迹图确认最优的岭参数,提高了网络的训练效果和泛化能力,在800 个训练样本条件下可以将平均色差控制在1.65 个CIE 色差单位。洪亮等[8]采用学习速度和泛化能力更好的RBF 神经网络来进行颜色空间转换,将等间隔采样的216 个色块作为训练集,在计算机上进行仿真实验,将平均色差控制在0.75 个色差单位,取得了不错的效果。Hajipour 等[9]将竞争神经网络与BP 神经网络结合,并进行特性化处理,先使用竞争神经网络对数据进行分类,再对分类后的数据分别使用BP 神经网络进行颜色空间转换。这种方法可将平均色差控制在一个较低范围,但是他们使用了1 500组样本来训练网络。总体来说,人工神经网络对非线性映射关系具有极强的拟合能力,在计算机算力和样本量足够的情况下,采用神经网络的方式进行颜色空间的转换,能够取得传统方法无法比拟的转换精度。
上述3 类主流方法各有优劣,整体来看,对精度要求不高的场景可使用较简单的传统方法,对精度要求高的场景可选择神经网络模型法。随着计算机硬件的发展,普通计算机就可完成神经网络训练,其计算能力不再限制该类方法的应用,但是训练样本需求量大、人工采集成本高仍限制了神经网络模型法的应用。构建特性化训练集的特点是需要人工使用测色设备逐个采集,并且每次特性化都需采集目标设备的训练集,整个样本的构建过程费时、费力。为了解决建立颜色空间转换关系需求样本量大、样本采集成本高等问题,文中将捕捉未知分布能力较强的生成对抗网络[10-12]应用于颜色空间转换任务中,添加校正模块,并设计多阶段训练方法,旨在小样本学习条件下,将不同颜色空间转换的精度控制在可接受范围内。
1 生成对抗网络
生成对抗网络(GAN,Generative Adversarial Network)于2014 年由Goodfellow 等[13]提出,是文中的核心网络架构,这里将介绍基础的GAN 模型和当前主流的WGAN(Wasserstein Generative Adversarial Network)[14-15]模型。
在训练过程中,GAN 模型无须马尔科夫链进行反复采样,也无须在学习过程中进行推断,回避了棘手的概率计算难题,其巧妙的设计在提出后便受到广泛关注。实验数据证明,该模型能够有效捕捉数据分布,是近年来复杂分布上无监督学习的主要方法之一。
基础GAN 模型包含生成模块和判别模块等,其模型如图1 所示。生成模块的作用是学习真实数据的分布,判别模块的作用是区分生成模块生成的数据和训练集的真实数据。模型的训练过程是让2 个模块进行博弈,通过2 个模块之间的博弈和交替训练,使整个模型逼近纳什均衡,最终使判别模块无法区分生成数据和真实数据,同时生成模块也学习到了真实数据的分布,生成的数据达到了以假乱真的程度。
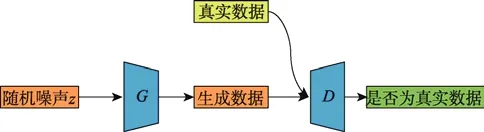
图1 生成对抗网络Fig.1 Generative adversarial networks
式中:G为生成模块;G(z) 为生成模块的生成数据;D为判别模块;x为真实样本;p(x)为真实样本分布;z为随机噪声;q(z)为随机噪声分布。
WGAN 对GAN 模型进行了重要改进,核心改动是将损失函数替换为Wasserstein 距离的对偶形式,如式(1)所示。WGAN 解决了GAN 训练不稳定、模式崩溃等问题,自2016 年被提出以来,就广泛应用于数据增强、小样本学习等领域,并且取得了不错的效果。
2 文中方法
基于WGAN 模型思想设计了具有校正功能的Cor−WGAN 模型,并设计了相应的多阶段训练方法来训练模型,利用不同模块的特点提高颜色空间之间的转换精度。这里将按照生成模块、判别模块、校正模块的顺序详细介绍Cor−WGAN 模型的结构,最后列出相应的多阶段训练方法的步骤。
2.1 融合多通道校正的Cor−WGAN 模型
基于生成对抗网络思想,文中设计了融合多通道校正模块的Cor−WGAN 模型,包含用于无监督学习的生成模块(Generator)和判别模块(Discriminator),以及有监督学习的校正模块(Correction),完整的模型结构如图2 所示。
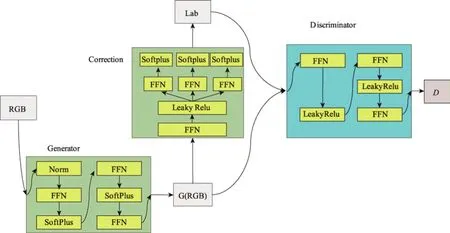
图2 Cor−WGAN 模型结构Fig.2 Cor-WGAN model structure
2.1.1 生成模块
生成模块的作用是学习RGB 到CIELab 颜色空间的转换关系,模块的输入是R、G、B,模块的输出是转换后的L、a、b。
R、G、B的值为0~255,为了加速网络的收敛,需要对数据进行归一化处理。数据生成模型常用的激活函数为Relu。由于使用Relu 可能会出现神经元死亡的问题,因此选择Softplus 来避免神经元死亡。
综上可知,生成模块的最终结构包括归一化层,2 个部分256 个神经元的FFN 配合SoftPlus 激活函数,以及3 个神经元的全连接层,将其作为输出层。
2.1.2 判别模块
判别模块的作用是学会如何计算输入的真实分布与生成分布之间的距离。模块的输入包含2 个部分:真实的L、a、b;生成模块生成的L、a、b。将2 个部分的数据输入判别模块,经过判别模块处理,输出Wasserstein 距离D,表示2 个部分数据分布之间的距离。由于判别模块计算的是分布距离,并不是计算该组数据为真实数据的概率,需要避免使用改变数据分布情况的操作,因此判别模块不使用归一化激活函数或者数据归一化等操作。
综上可知,判别模块的最终结构包括2 个部分的256 个神经元的FFN 配合LeakyRelu 激活函数,以及1 个神经元的全连接层,将其作为输出层。
2.1.3 校正模块
纳什均衡是一种理想状态,在实际训练过程中往往很难达到真正的纳什均衡。体现在数据上,即生成数据只能逼近真实数据,当色差减小至一定程度时,网络训练的边际效应变得十分明显。为了克服这一缺点,笔者设计了多通道校正模块,为生成模块提供校正建议。校正模块结构如图3 所示。
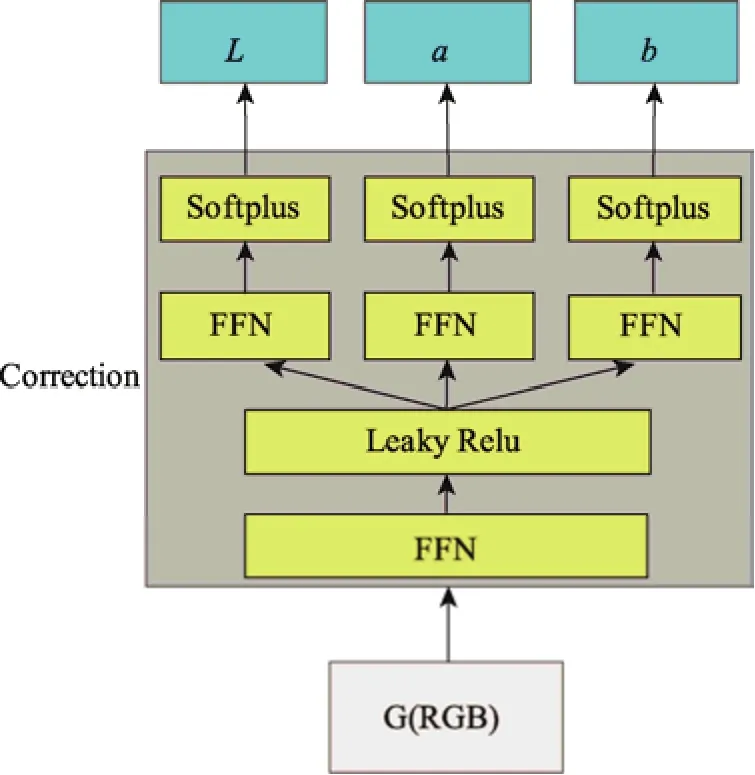
图3 多通道校正模块Fig.3 Multi-channel calibration module
针对L、a、b分别给出了独立的校正建议,将校正模块设计为多通道结构,让每个通道单独考虑1 个值的建议。在生成模块和判别模块的无监督学习完成后,校正模块和生成模块会进行有监督学习。校正模块的输入是生成模块生成的数据G(RGB),输出是L、a、b等值的校正建议,将真实的L、a、b作为校正模块的标签。
在数据进入校正模块后,先经过512 个神经元的前馈神经网络FFN,再由激活函数Leaky Relu,筛选出部分不可用的连接,接着分为3 个通道,对应亮度值L、红绿彩色通道值a、黄蓝彩色通道值b,再经过64 个神经元的前馈神经网络FFN 及SoftPlus 激活函数,最终得到模块输出。
校正模块的作用是在生成模块和判别模块无法达到真正的全局最小值时,分别从L、a、b等3 个角度给出调整建议,生成模块据此再次微调模型的权重,使生成数据更加接近真实数据。
2.2 多阶段训练方法
深度学习的训练方法通常采用输入到输出的正向传播,再根据损失函数计算loss 值,求得梯度后反向传播,以更新整个模型的参数。这里提出的模型采用了模块化思想,模块之间参数的更新过程相对独立,常用的一次性更新整个模型的方法会让收敛困难,甚至无法收敛。为此,这里设计了多阶段训练方法,包含预训练、无监督对抗训练和校正训练3 个部分,以提升小样本下模型的收敛速度,整体流程如图4 所示。
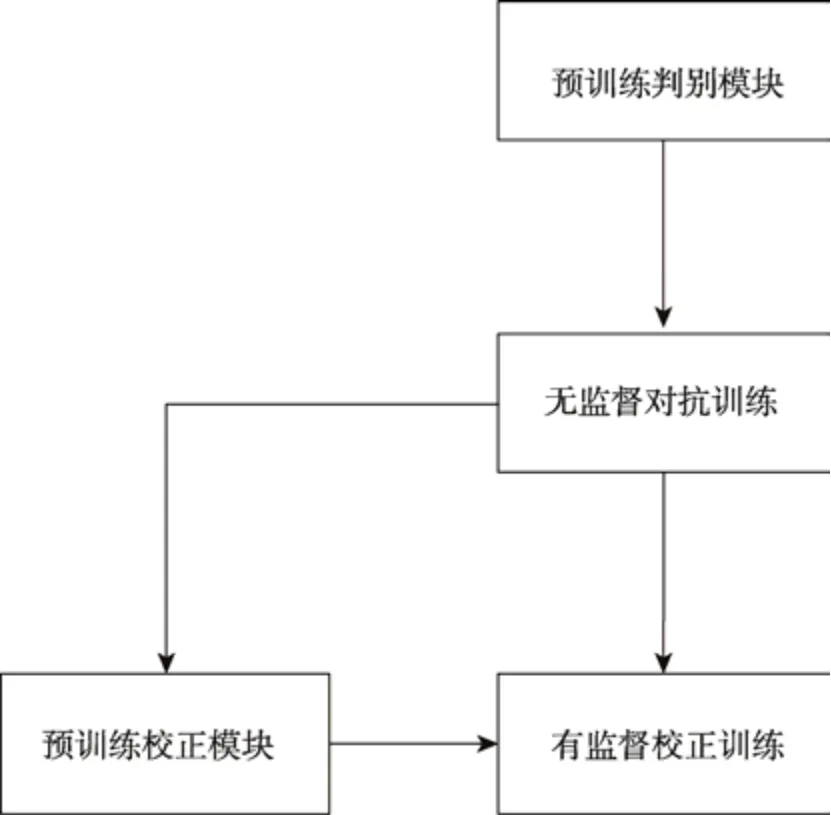
图4 多阶段训练方法流程Fig.4 Multi-stage training method flow
在模型尚未训练阶段,各个模块都不具备相应的能力。其中,最关键的是判别模块无法判断最基本的真实数据与生成数据的区别,而不具备判别能力的判别模块无法在无监督学习中检验生成模块的生成效果。由此可见,在进行模块之间相互对抗训练前,需要对判别模块进行预训练,赋予判别模块判断差异较大真假数据的能力。
经过一定的预训练轮次,判别模块具备一定的判断能力后,再根据式(1)所示的损失函数,启动判别模块和生成模块相互博弈的无监督对抗训练。在每个轮次的对抗训练中,优先训练判别模块,提升判别模块的判别能力。训练后的判别模块计算生成分布与真实分布的Wasserstein 距离会更大,再以减少分布距离为目的来更新生成模块的权重,提升生成模块的生成能力,相互博弈前进。
完成了判别模块和生成模块的无监督对抗训练后,判别模块具备了较好的判别能力,生成模块生成的数据也会逼近目标颜色空间颜色值分布,再进行校正训练。首先对校正模块进行预训练,学习给出多通道校正建议的能力,再将生成模块与校正模块配合,以均方误差为损失函数开始校正训练。在每个轮次的训练中,优先训练校正模块,以提升校正能力,再调整生成模块,以提升生成数据的质量。
3 实验设计与结果
这里将通过实验来验证文中提出方法的有效性。首先在标准颜色空间下,通过对比不同方法之间的转换精度,验证文中算法在小样本颜色空间转换时的效果。通过调整训练集的大小来对比文中方法在不同大小样本条件下的转换精度,通过消融实验来证明文中方法有助于提升颜色空间转换的精度。最后,设置非标准颜色空间仿真实验和逆转换实验,验证文中方法在实际应用中的效果。
3.1 构建标准颜色空间训练集
这里采用的是小样本学习,为了避免Cor−WGAN模型只学习局部的转换关系,需要训练集尽可能均匀地分布在整个颜色空间。在标准颜色空间实验阶段,将0~255 的R、G、B数据等间隔划分,以获取均匀分布的训练集。以四等份(0、85、170、255)为例,将R、G、B四等分的颜色值互相组合,得到64 个色块,根据标准转换公式将R、G、B转换为D65 光源/2°视场观察条件下的L、a、b。将得到的64 组标准颜色空间R、G、B,以及L、a、b作为模型的训练样本,示例样本如图5 所示。
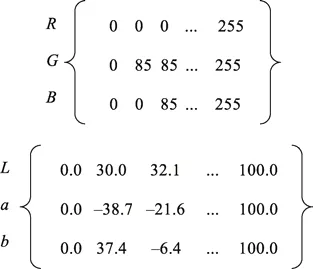
图5 四等份训练数据示例Fig.5 Example of quartered training data
3.2 实验设计
以文中构建的均匀样本为训练集,通过Pytorch深度学习框架搭建Cor−WGAN 的网络结构。
1)网络训练。先对判别模块进行1 000 轮的预训练,让其先具备一定的判别能力,然后由生成模块和判别模块进行10 000 轮无监督对抗学习,每轮训练判别模块3 次,训练生成模块1 次。在完成无监督学习后,使用校正模块和生成模块进行5 000 轮有监督学习,调整生成模块的生成效果。
2)参数优化。优化器均使用Adam(平滑参数分别取0.7 和0.9),初始学习率均为0.005。
3)对照组。选择基于RBF 神经网络[3]和R−ELM[8]的颜色空间转换方法为对照组,训练数据集、优化器、学习率等都采用相同的设置,迭代数量设置为10 000次,同样选择Pytorch 框架搭建网络结构。
在Pycharm 集成开发环境下对上述3 个网络进行训练,并以Pantone 国际标准色卡数据集的907 组标准颜色空间RGB 数据和Lab 数据为测试集。针对上述网络转换效果,使用Lab 颜色空间的色差公式对结果进行评价,色差公式如式(2)所示。
式中:x和y为2 个色样;L*为明度指数;a*为红绿色度指数;b*为蓝黄色度指数。
3.3 不同方法的对比实验
验证不同算法在小样本条件下的转换效果,使用64组标准颜色空间样本训练R−ELM、RBF 神经网络、Cor−WGAN 模型后,将测试集的R、G、B 输入训练完成的网络中,得到模型输出和训练集的L、a、b真实值,计算色差,结果如表1 所示。对应的色差分布如图6 所示。
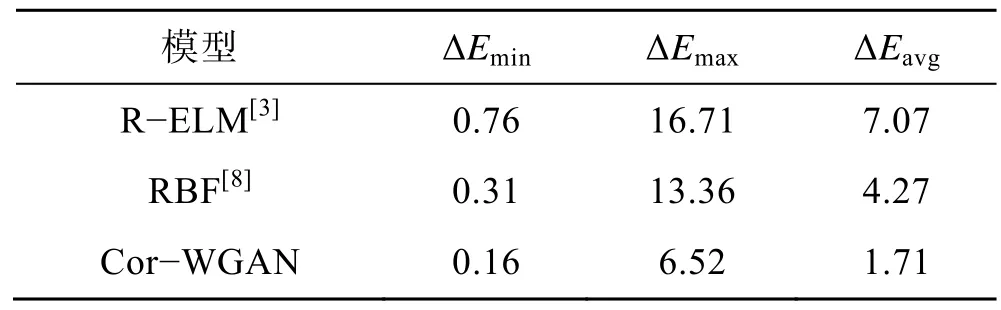
表1 不同方法的色差比较Tab.1 Comparison of color difference of different methods
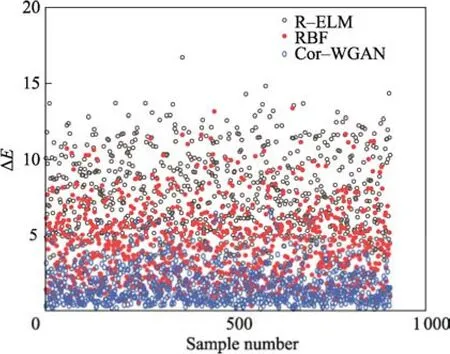
图6 不同方法色差分布Fig.6 Color difference distribution of different methods
实验结果表明,在小样本条件下,文中提出的Cor−WGAN 模型不论在平均色差、最大色差还是最小色差上,都比R−ELM 极限学习机和RBF 神经网络表现得更好。
3.4 不同数据集的对比实验
为了对比Cor−WGAN 在不同训练集上的效果,这里将0~255 的R、G、B等数据进行不同程度的等间隔划分,再进行组合,分别设计了三等份(0、127、254)实验组(共27 个训练样本)、四等份(0、85、270、255)实验组(共64 个训练样本)、五等份(0、63、126、189、252)实验组(共125 个训练样本)、六等份实验组(0、50、100、150、200、255)实验组(共216 个训练样本)。将Pantone 国际标准色卡作为测试集,得到的平均色差如表2 所示。

表2 不同算法在不同训练集上的色差比较Tab.2 Color difference comparison of different algorithms in different sizes of training sets
不同实验对照组的数据都尽量平均分布在整个RGB 颜色空间中。由于RGB 颜色空间不是均匀的颜色空间,因此在27 个样本的情况下,3 种方法都无法学习到完整的分布特征,其中Cor−WGAN 是转换效果最好的一组。
在扩大训练集时,样本在颜色空间中分布得更加密集,模型可学习到颜色空间中不均匀部分的转换关系。从实验结果可知,当训练样本扩大到125 个时,3 种方法的转换效果都得到较大提升,且都满足色差小于6 的国标印染要求。当训练样本扩大到216 个时,所有对照组的色差都小于3,按照文献[16]的评判标准,它们均达到了人眼无法分辨的程度。
综上可知,Cor−WGAN 网络模型只需64 对训练样本就满足日常生活的色彩转换需求,充分证明该模型具有优秀的小样本学习能力。
3.5 消融实验
为了验证多通道校正模块的效果,这里设计了包含完整Cor−WGAN 模型组、单通道校正模块组和删除校正模块组3 个对照组的消融实验,训练集使用标准颜色空间的64 组均匀样本,测试集使用Pantone 国际标准色卡数据,结果如表3 所示,色差分布如图7 所示。
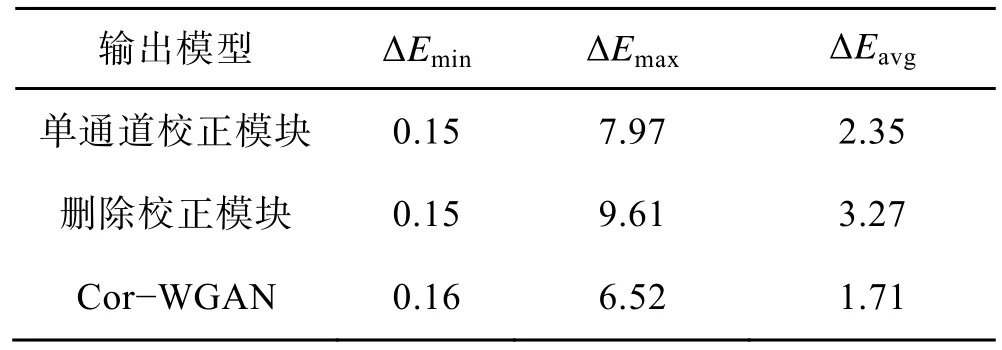
表3 消融实验的色差比较Tab.3 Color difference comparison of ablation experiment
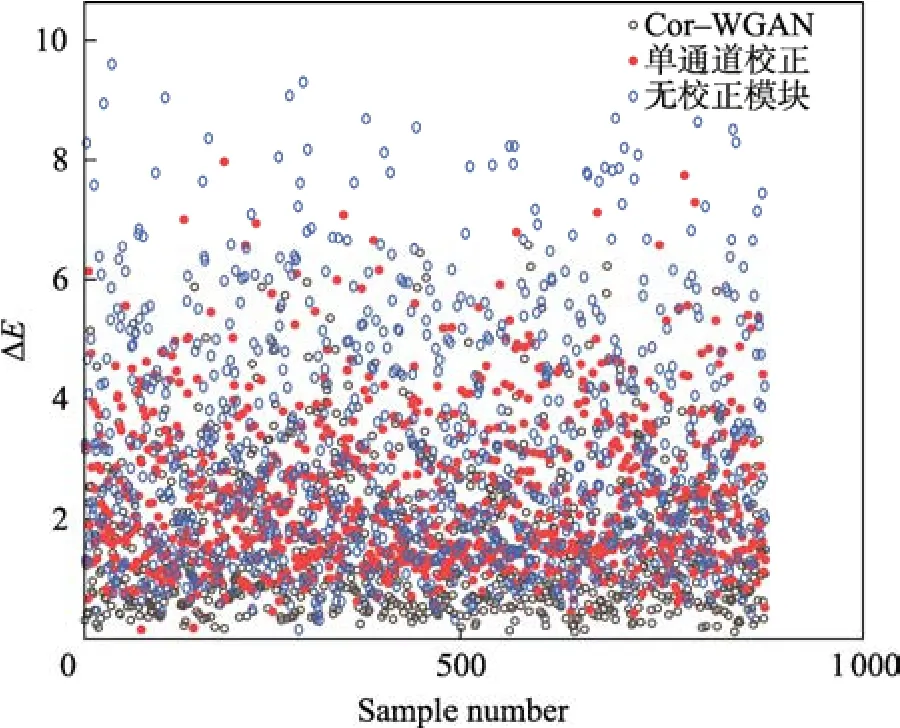
图7 消融实验色差分布Fig.7 Color difference distribution of ablation experiment
表3 前2 行数据表明,使用单通道校正模块与多通道校正模块存在差异。在计算过程中,由于单通道校正模块L、a、b等3 个输出值共用单通道神经元,导致输出值之间存在相关性,因此最终输出校正建议时也会折中。这与表3 中的实验结果相互印证,单通道校正模块对生成模块的调整有限,导致模型最终输出的平均色差更高。
表3 第1 行和第3 行数据表明了校正模块对整个模型的意义。如果完全移除校正模块,则输出结果即为生成模块和判别模块无监督对抗训练的结果。由于生成对抗网络本身具有难以达到纳什均衡的缺陷,因此不使用校正模块的平均色差达到3.27 个CIE 色差单位。
整个消融实验的结果表明,多通道校正模块给出的独立校正建议更有利于修正WGAN 模型的输出结果,文中提出的改进模型有利于提高颜色空间的转换精度。
3.6 非标准颜色空间仿真实验
上述实验表明,文中提出的Cor−WGAN 模型在标准颜色空间下取得了较好的效果。为了验证模型在实际应用中的转换效果,这里设计了计算机仿真函数来模拟非标准颜色空间转换关系。
仿真函数的具体实现方式:在标准的RGB 向XYZ 转换过程中添加0.99~1.01 的随机参数,再通过XYZ 颜色空间转换到 D65 光源/2°观察条件下的CIELab 颜色空间,以此来模拟转换关系的随机变化,核心公式如式(3)所示。
式中:X、Y、Z为三刺激值;r、g、b分别为归一化修正后的R、G、B值;βi为随机参数。
分别设置27、64、125、216 等4 组不同程度均匀等分样本的对照组。训练集部分使用等间隔划分的训练样本,对应的L、a、b真实值通过仿真函数计算。在测试集部分,使用随机的R、G、B作为R−ELM、RBF 和Cor−WGAN 模型的输入,再通过模型预测的输出值L、a、b与仿真函数输出值L、a、b计算色差,实验结果如表4 所示。
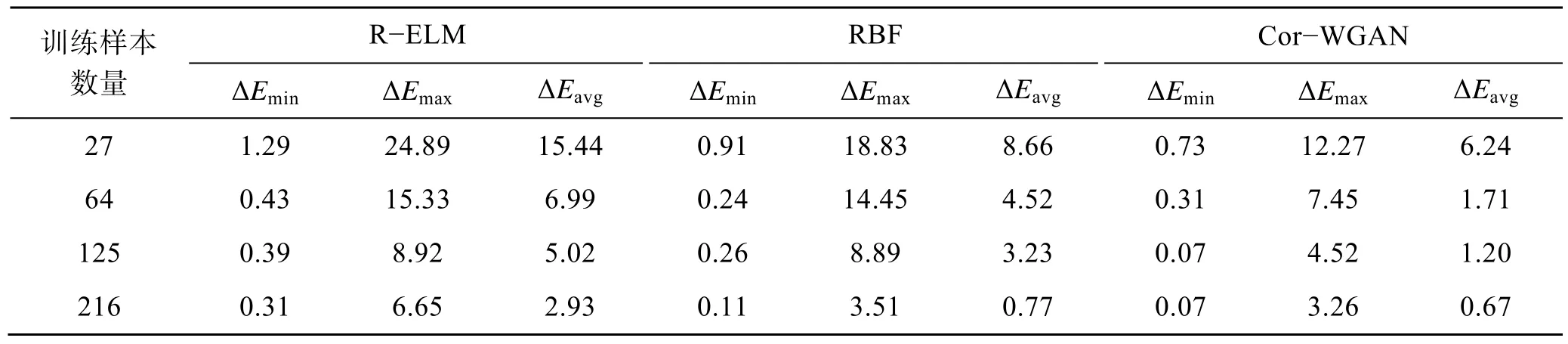
表4 不同算法在非标准颜色空间实验的色差比较Tab.4 Color difference comparison of different algorithms in non-standard color space experiment
从实验结果可以看出,文中提出的Cor−WGAN模型在非标准颜色空间下依然取得不错的转换效果,且能够完成小样本学习任务。
3.7 逆转换实验
在实际应用中,色彩管理系统会采用中间颜色空间为媒介,完成不同设备颜色空间之间的转换。中间颜色空间一般是与设备无关的颜色空间,CIELab 就是一种常用的中间颜色空间。
这里设计了RGB 到CIELab 颜色空间的逆转换实验,以验证模型从中间颜色空间转换到目标颜色空间的学习效果。对比分析R−ELM、RBF 和Cor−WGAN模型,训练集为27、64、125、216 组非标准颜色空间仿真样本,仿真过程中的随机参数取0.99~1.01。
在逆转换实验中,模型的输入值为L、a、b,模型的输出值是转换后的R、G、B,模型的输出值与对应的R、G、B真实值按照式(4)求得单组实验数据的色差,12 组实验的色差对比如表5 所示。
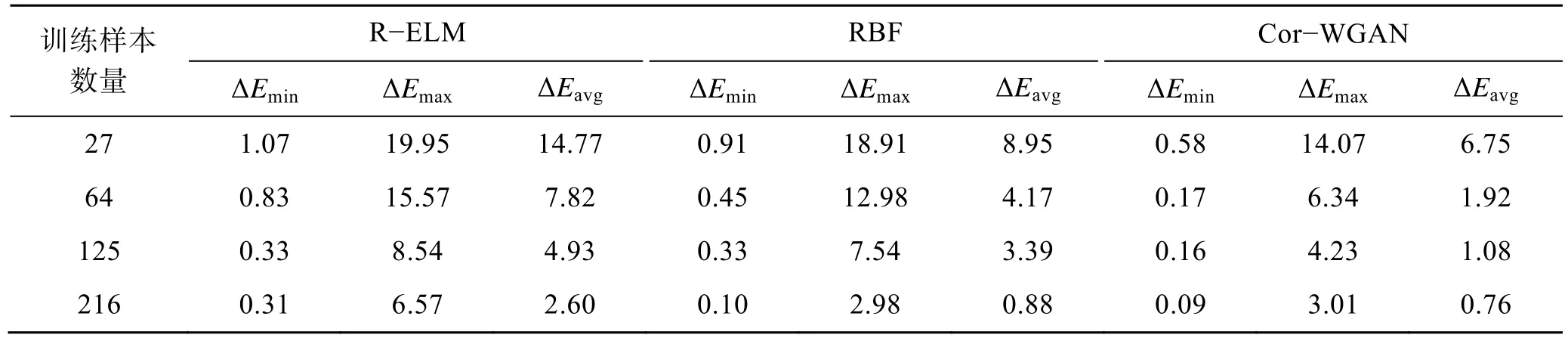
表5 不同算法在逆转换实验中的色差比较Tab.5 Color difference comparison of different algorithms in inverse conversion experiment
实验结果表明,文中提出的Cor−WGAN 模型在小样本条件下依然具有十分明显的优势,在 64组样本条件下的训练结果满足国标要求,R−ELM和RBF 都需要至少216 个样本才能达到相应的转换效果。
4 结语
以WGAN 模型为基础,提出了一种融合多通道校正模块的Cor−WGAN 颜色空间转换模型,可以在小样本情况下学习到由RGB 到CIELab 颜色空间的转换关系。实验结果表明,相较于现有的颜色空间转换方法,文中提出的方法在小样本情况下有着更加优秀的表现,且在增大样本容量的情况下,此方法依然具有竞争力。后续的非标准颜色空间仿真实验和逆转换实验表明,文中提出的方法可以在实际应用中保持较好的转换精度,为基于深度学习的色彩管理应用提供了一种切实可行的思路。

