基于倾斜摄影三维网格模型的建筑物轮廓提取研究

张文政

摘要：轮廓是建筑物的基本特征，在倾斜摄影测量与地理信息领域一直是一个热门话题，传统的轮廓提取需要在三维模型上的每面墙体选点生成轮廓，这种方法费时费力。文章提出一种基于倾斜摄影三维网格模型的建筑物轮廓提取方法，首先，通过一种自适应阈值的方法进行建筑物边缘三角网格检测；然后，将其栅格化，通过Suzuki轮廓跟踪算法获取建筑物轮廓；最后，基于Douglas-Peucker算法获得简化轮廓。实验结果表明，文章所提算法是一种有效的三维建筑物轮廓提取方法。

关键词：倾斜摄影测量；三维网格；边缘检测；轮廓提取

中图分类号：TP39  文献标志码：A

0 引言

建筑物是城市中不可或缺的组成部分，而建筑物的边缘与轮廓涵盖了建筑物的几何形状和地理位置等信息，对于城乡地籍管理、三维重建以及智慧城市具有不可替代的作用，传统的建筑物边缘与轮廓提取是基于图像数据进行处理的，但是图像数据易受到分辨率、树木遮挡等因素影响导致信息缺失，三维领域主要是基于点云进行提取［1-2］。点云精度很高，但是点云的制作成本较高，随着倾斜摄影测量技术的出现，带来了新的解决方法，该技术通过无人机携带五镜头摄像机按照规定轨道飞行，通过拍摄不同视角的照片，结合空三测量即可生成高精度的三维模型［3］。这种三维模型具有卓越的几何信息和纹理信息，而且精度较高，受到广大测绘人员的喜爱，但由于是新生代技术，相关研究主要基于商业软件，如EPS测图软件、DP mapper测图软件、Hi Data航测软件等，通过人工对三维建筑物上的每面墙体进行选点［4-6］，基于散点正交的原理生成建筑物轮廓。这种方式原理简单，但是需要大量人工的投入，在实际生产中效率较低。

基于倾斜摄影测量技术生成的实景三维模型具有丰富的几何信息，其中主要包括三角网格数据与倾斜点云数据。三角网格数据是由一系列高精度的起伏三角形构成，可以真实地反映地表情况，而点云数据相对散乱，反映地表情况的能力欠佳，所以在需要利用地表特征的情况下优选三角网格数据。对于建筑物而言，通常由墙体、屋顶以及阳台3个部分组成，这3个部分具有明显的特征，墙体一般垂直于地面，屋顶为倾斜平面或水平平面，阳台则是由平面和垂直边组成，因此本文选择三角网格作为研究对象。

建筑物的边缘通常是由墙面以及阳台的垂直边缘组成，为此只需要求取到合适的垂直立面三角形即可获取建筑物的边缘，而轮廓则是边缘中最外闭合的一圈，为此本文设计一种自适应阈值的边缘检测方法，并将其栅格化为二值图像，借助图像处理中经典的Suzuki轮廓跟踪算法获取建筑物的最外轮廓［7］。由于此时轮廓锯齿较多，所以本文通过Douglas-Peucker算法对其简化［8］，并在山东省威海市环翠区选择数据进行了验证。

1 数据介绍

本文选择威海市环翠区环翠家园住宅区作为研究区域，选取了其中13个长度与形状各异的建筑物，其中5个建筑物属于直角方形建筑物，8个建筑物属于弧形建筑物，这13个建筑物都具有多個墙面，平面结构为凹多边形。该选区的三维模型通过大疆经纬M300 RTK航拍无人机搭载4 500万像素的禅思P1镜头拍摄，并通过ContextCapture软件生成，模型的平面精度为5 cm，如图1（a）所示。为了方便后续的处理，读取了每个建筑物单独的三维网格数据，如图1（b）所示，这些网格数据由一系列三角形拼接而成，可以真实地反映建筑物的地表情况。

2 基于自适应阈值的边缘网格检测

良好的边缘能够为后续的轮廓提取提供较大的助力，建筑物的边缘集中于墙体立面与阳台立面，这些立面的三角形法向量与地面平行，所以只要获取到符合条件的三角形即可。但是由于地形以及建模可能带来的误差，这个阈值并不好确定，给定固定值可能不适用于所有建筑物，为此需要设计一个自适应阈值。

对于三维空间中一个单独的三角形，设为T，顶点为（A，B，C），法向量设为ON，法向量ON可由三角形的两条边的方向向量叉乘所得，点N′为点N在XY平面的投影点，θ为法向量ON与XOY平面之间的夹角，如图2所示，θ可表示为：tanθ=z（x2+y2），θ=arctanz（x2+y2）。

θ的大小可以反映出三角网格的倾斜情况。θ值是基于法向量计算所得，而法向量与三角形垂直，故θ值与三角网格的倾斜度呈负相关，即θ值越小，三角形倾斜程度越大，因此将其命名为倾斜角。根据此特性，将建筑物陡峭墙面的三角形与平缓平面的三角形分离出来，建筑物的垂直面倾斜角理论上应高度聚合于0°附近，但是由于模型差异导致倾斜角不固定，已知垂直面倾斜角一定位于［-30°，30°］区间，以选区中的一个建筑物为例进行边缘检测过程展示，三维模型如图3（a）所示，图3（b）为其三角网格数据，对该建筑物位于［-30°，30°］区间的三角形进行倾斜角统计，获得频数分布直方图，如图3（c）所示。通过研究发现这部分的三角形倾斜角在直方图中接近正态分布的特征，为了保留尽可能纯净的垂直墙面，以及自适应取值，本文选取倾斜角位于均值μ±一倍标准差σ范围的三角形作为研究数据，选取结果如图3（d）所示。

垂直面除了代表边缘的立面，还包括一些屋顶、地面和植被的垂直面等。由于建筑物周边的植被与地面等垂直面大多数是低矮的，而屋顶高度一般会高于整体高度的2/3，根据经验选取三角形高度位于整体建筑物高度1/3～2/3的部分，以此获取较为纯净的边缘数据，如图4（a）所示，并将其投影到二维平面作为边缘数据，如图4（b）所示。

建筑物边缘检测总体流程如图5所示。

3 轮廓提取与简化

由于边缘提取后的结果是离散的不规则三角形数据，在平面分布不均匀，为此通过规则正方形将其栅格化，主要步骤分为两步。

（1）确立网格的尺寸：网格尺寸需要考虑到每个边缘三角形的宽度，以及建筑物墙体的长度，经过综合考量，将三角形3条边上最短的高认为是这个三角形的宽度，计算平均宽度，尺寸设置为平均宽度的2～3倍。

（2）進行网格化：通过判别三角形与网格是否相交的方法进行网格化，若是相交，则将网格记为1，无数据区则记为0，网格化的结果便生成了二值图像，网格化方法如图6所示。

将上文获取的建筑物边缘按上述的步骤网格化，生成的二值图像如图7所示，可以看出规则化的图像与原始边缘数据基本保持吻合。

生成二值图像后，即可使用经典的Suzuki算法进行轮廓跟踪。Suzuki算法是一种连通区域标记算法，通过使用Freeman链码的方式获取轮廓编码，其基本思想是扫描图像，寻找满足条件的边界跟踪起始点，再执行边界跟踪，找到所有的边界，在边界跟踪时通过对每个边界赋予的数字标号来区分不同的轮廓。该算法已经由OpenCV图像处理库封装，函数名为findContours（），通过该函数可以获取二值图像中的所有轮廓或者最大轮廓，同时可以选择轮廓存储方法，包括Freeman链码、点集和简化点等方法，简化的方法只保留了线段端点，去除了线段中间的点，而本文中轮廓主要为二值图像的最外轮廓，也就是最大的轮廓，故选择最大轮廓和简化点存储方法。

轮廓的点集中即使只保留了线段端点，也依然存在大量的冗余点，所以需要进行轮廓数据的简化。Douglas-Peucker算法便是一种优良的数据简化方法，具有平移和旋转不变性的优点，再加上通过距离计算阈值，方法简单，执行效率较高，而且该算法抽稀结果与原始数据一定，使得该算法被普遍应用于实际生产中数据压缩场景。针对上文获得的轮廓数据，使用Douglas-Peucker算法进行简化，具体步骤如下：

（1）设定距离阈值。距离阈值越大，轮廓的简化程度越大，容易失去原始形状，反之，简化程度则较低，最终选取阈值为0.2 m。

（2）从轮廓点集中连接起点与终点，形成一条直线，计算其他轮廓点到这条直线的距离。

（3）找到距离最远的一个点，判断距离是否大于阈值。若是大于，则将其保留；若是小于，则用这条直线代替这段点集。

（4）以这个点为新的分界点，将原先边缘点集分为两组，分别对这两段数据执行步骤（2）（3）的处理。

（5）对所有点进行判别后，依次连接保留的点，将结果作为简化轮廓数据，如图8所示。

4 实验与分析

对选区倾斜摄影方式生成的三维建筑物三角网格数据，利用自适应倾斜角阈值与高度阈值提取建筑物的边缘三角形数据，如图9所示，发现这13个建筑物的边缘基本符合各自的轮廓特征，在地理位置上偏差不大。这是因为使用的是原始的垂直立面三角形进行了投影，在实验过程中，也发现在原始建筑物墙体三角网格不缺失的情况下，边缘数据不存在断裂情况，而且该方法不局限于单一类型的建筑物，具有通用性，能够为后续的轮廓提取提供良好的数据支撑。

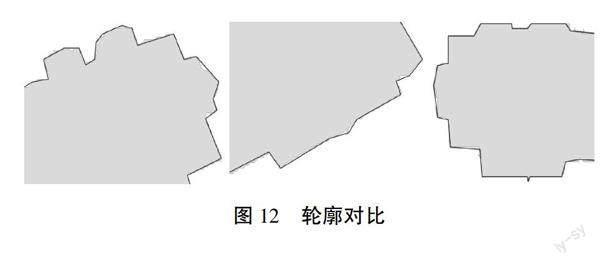
获取边缘数据后，对每个建筑物边缘栅格化，生成二值图，并通过Suzuki算法获取最大的外轮廓，如图10所示。通过目视解译可以发现：Suzuki算法所提取的轮廓锯齿化严重，为此使用Douglas-Peucker算法简化轮廓，达到去除锯齿的效果，结果如图11所示。同时将两种建筑物类型的简化轮廓与原始轮廓进行叠加对比，如图12所示，其中面状图形为原始轮廓，线状图形为简化轮廓，可以看出Douglas-Peucker算法对于本文所提取的轮廓重要信息保留较好，同时去除锯齿效果也较好。

在这组数据中，建筑物的类型丰富，不仅有规则的方形建筑物，还有不规则的弧形建筑物，而且最后的轮廓结果也表明本文的方法对于凹多边形适用，现有的方法对凹多边形建筑物的处理总是不够良好，而本文的方法对建筑物的凹角信息保留较好。

5 结语

本文在倾斜摄影三维模型的基础上，从内部的三角网格出发，通过对三角网格法向量倾斜角的讨论，设计了一种自适应阈值，并且通过高程阈值得到了较为纯净的建筑物边缘，之后通过将边缘栅格化的方法使其成为规则的二值图像，通过Suzuki算法结合      Douglas-Peucker算法实现建筑物轮廓的提取与简化。实验结果表明，本文的方法对于规则建筑物和不规则建筑物都具有普适性，同时对建筑物的凹角信息保留较好。

参考文献

［1］高智梅，王竞雪，沈昭宇.机载LiDAR建筑物点云渐进提取算法［J］.测绘通报，2021（8）：7-13，36.

［2］AWRANGJEB M.Using point cloud data to identify，trace and regularize the outlines of buildings［J］.International Journal of Remote Sensing，2016（3）：551-579.

［3］郝祥侠，王新鹏.倾斜摄影测量技术在房地一体中的应用［J］.水利技术监督，2023（1）：53-55，156.

［4］许承权，滕明星.一种新的立体测图方法［J］.城市勘测，2019（2）：143-146.

［5］李柳春，姚皖路，赵俊三.基于倾斜三维模型利用EPS制作大比例尺地形图［J］.中国水运，2021（2）：23-25.

［6］宋媛媛，张照杰，刘明涛，等.无人机实景三维模型在大比例尺地形图测绘中的应用［J］.测绘与空间地理信息，2022（6）：226-228.

［7］SUZUKI S，BE K.Topological structural analysis of digitized binary images by border following［J］.Computer Vision，Graphics，and Image Processing，1985（1）：32-46.

［8］DOUGLAS D H，PEUCKER T K.Algorithms for the reduction of the number of points required to represent a digitized line or its caricature［J］.Cartographica：The International Journal for Geographic Information and Geovisualization，1973（2）：112-122.

（編辑 沈 强）

Research on building contour extraction based on 3D mesh model of oblique photography

Zhang  Wenzheng

（School of Geography，Geomatics and Planning，Jiangsu Normal University， Xuzhou 221116， China）

Abstract：  Contour is the basic feature of buildings. It has always been a hot topic in the field of oblique photogrammetry and geographic information. The traditional contour extraction needs to select points on each wall of the 3D model to generate the contour. This method is time-consuming and laborious. This paper proposes a method of building contour extraction based on the 3D mesh model of oblique photogrammetry. First， an adaptive threshold method is used for building edge triangular mesh detection， Then it is rasterized， and the building contour is obtained through Suzuki contour tracking algorithm. Finally， the simplified contour is obtained based on Douglas-Peucker algorithm. The experimental results show that the proposed algorithm is an effective three-dimensional building contour extraction method.

Key words： oblique photogrammetry; 3D mesh; edge detection; contour extraction