基于蒙特卡罗模拟法的柔性交直流混联配电网概率潮流计算

孙银锋,夏大朋,高梓淳

(1.东北电力大学电气工程学院,吉林 吉林 132012;2.国网东营供电公司,山东 东营 257091)

0 引 言

在“双碳”背景下,新能源发电在电力系统中的占比有望进一步提高[1]。同时,风电和光伏等新能源的输出功率具有波动性和不确定性,也给电网的运行控制带来了严峻的挑战[2]。如何针对新能源不确定性和系统多运行方式条件下获得电网的潮流分布,成为了电力调度部门亟需解决的问题。

1974年,Borkowaka提出概率潮流计算方法[3]。发展至今,概率潮流问题求解方法可分为模拟法[4-6]、近似法[7-8]和解析法[9-11]。概率潮流计算方法在交流系统已经被广泛应用。然而,电网运行人员同样急需高效准确的交直流混联系统概率潮流计算方法,以获得新型的交直流混合配电网的稳态信息。目前,国内外学者在交直流混联系统的概率潮流算法上已经取得了一定的成果。文献[12]针对传统无迹变换在处理高维概率潮流计算时,随着交直流混联电网中随机变量维数增加计算精度会下降的问题。提出用比例伸缩无迹变换处理高维高斯分布的方法,将无迹变换算法用于含有电压源换流器(Voltage Source Converter,VSC)的柔性交直流混联电网概率潮流分析中,能够有效地解决高维概率潮流的精度问题。文献[13]以节点注入功率运行曲线构成系统的多运行方式,推导出不同控制方式下的交直流混联系统的概率潮流模型,以整流器定电流控制、逆变器定电压控制为例进行概率潮流分析,没能考虑换流器控制方式的多样性。同时,该系统采用的电流源换流器并不适合构成多节点的直流电网,因此该方法具有一定的局限性。文献[14]针对概率潮流计算中常规潮流的不收敛,建立了含风电场交直流混联系统概率潮流模型。采用改进的(Levenberg-Marquardt,LM)方法求解潮流非线性方程组,然后根据蒙特卡洛模拟法求解概率潮流分布,该方法具有较好的鲁棒性。文献[15]提出一种基于聚类的柔性交直流系统概率潮流算法。首先对不确定源进行聚类,然后由聚类中心进行交直流系统的概率潮流计算,该方法减少了计算量,且所得结果具有一定的可信度,但是没能考虑风机接入点对系统潮流分布的影响。文献[16]提出一种基于自适应扩散核密度估计的时序相关概率最优潮流计算方法,利用线性扩散的自适应特性提高了光伏出力估计模型的局部适应性,能够更为准确描述光伏输出功率的波动性与不确定性。并结合 Copula理论建立光伏与负荷的联合概率模型,得到具有相关性的光伏与负荷样本,验证了方法的有效性。

本文计及了风电、光伏及负荷的不确定性模型,针对含有VSC的交直流混合配电网特点,分别建立主从控制和下垂控制的概率潮流计算模型。为了准确评估系统的概率潮流分布,采用基于蒙特卡洛模拟的交替迭代法求解该潮流模型。通过风电、光伏不同穿透率以及不同接入比例的分析,研究了风光互补特性对概率潮流分布的影响。最后,在修改后的IEEE-34节点系统中进行计算对方法进行验证,为交直流混合配电网的规划设计提供参考。

1 交直流混联系统确定性潮流计算模型

图1中,i为第i个与直流电网连接的VSC;Rci、Xci分别为换流电抗器的等效电阻和等效电抗;PCC(Point of Common Coupling,PCC)为公共连接点;Usi、δsi分别为PCC处的交流基波电压幅值和相角,Uci、δci分别为换流器交流侧基波电压和相角;Ps、Qs分别为PCC点注入的交流有功功率和无功功率;Pc、Qc为交流系统向换流器交流出口处注入的交流有功功率和无功功率;udi、idi分别为直流侧的直流电压和电流。在忽略滤波器的情况下,换流电抗器和换流变压器的电抗合并,可以消除对复杂滤波器母线电压的依赖,滤波器母线和交流电网母线重合,从而简化方程[17,18]。

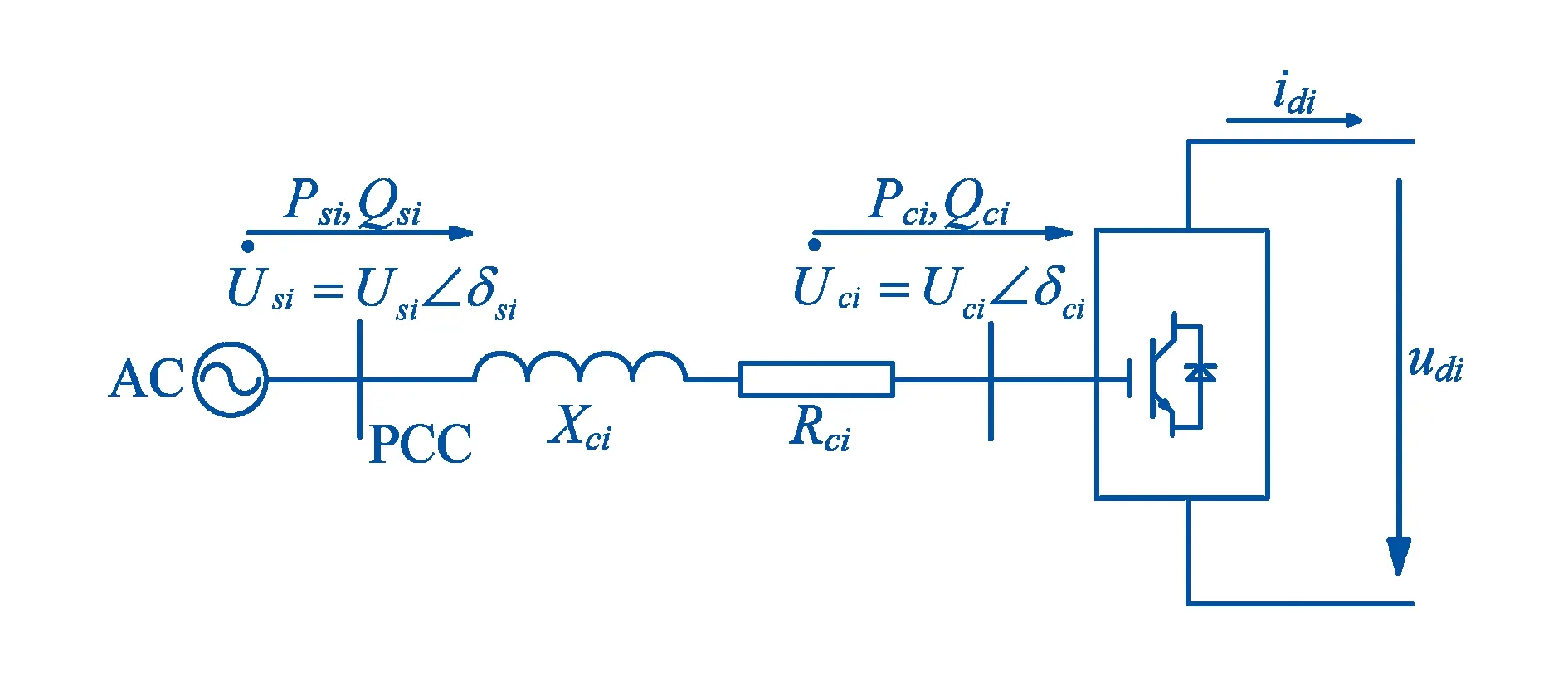
图1 VSC潮流计算模型Fig.1 VSC Power flow calculation model

交流系统极坐标形式的潮流模型,即

(1)

公式中:n为节点数;Pt和Qt分别为节点t注入有功功率和无功功率;Gtj与Btj分别为节点导纳矩阵的实部与虚部;δtj为节点t、j之间的相角差。Pst和Qst分别为节点i交流侧注入换流器的有功功率和无功功率。

其中,第i个VSC中:

(2)

则第i个VSC与交流母线之间传输的有功及无功功率分别为

(3)

公式中:μi、Mi为直流电压利用率及调制度;δi为VSC网侧与阀侧的相角差。

对于直流系统,直流功率Pdi等于交流系统注入VSC的功率,所以满足以下方程为

(4)

而在直流系统中,直流电流、直流电压和直流节点间的导纳满足关系为

(5)

公式中:nc为直流节点数;udj为直流电压;idi为直流电流;gdij为直流节点i和直流节点j之间的电导。

由公式(3)～公式(5)可求得[19]:

(6)

将公式(6)按照泰勒级数展开,略去高次项后,所得修正方程式一般形式为

ΔD=JΔX

(7)

其中,ΔD=[…,Δdi1,Δdi2,Δdi3,Δdi4,…]T,ΔX=[…,Δudi,Δidi,Δδi,ΔMi,…]T,J为雅可比矩阵。

目前,MTDC的运行需要换流站之间进行协调配合实现直流系统的功率平衡和直流电压稳定。MTDC的控制方式有主从控制、直流电压下垂控制等。

1)主从控制

在交直流潮流计算时换流器的主从控制方式主要有如下四种[20]。

1)控制Ps恒定、Qs恒定;2)控制Ps恒定、Us恒定;3)控制udc恒定、Qs恒定;4)控制udc恒定、Us恒定。

2)下垂控制

电压下垂控制原理图以多点直流电压控制为特征。如果直流电压由于网络中的功率缺额而下降,电压下垂控制站根据其自身的运行曲线增加注入网络的功率,依据控制量的不同,可分为功率特性(V-P)和电流特性(V-I),工作特性如图2和图3所示。功率特性控制和电流特性控制分别为[21]

Δfi=(udci-udcrefi)+kdroop(Pdci-Pdcrefi)=0

(8)

公式中:Udcrefi和Pdcrefi分别为系统运行参考节点;kdroop为下垂系数。

Δfi=(udci-udcrefi)+kdroop(idci-idcrefi)=0

(9)

公式中:Udcrefi和Idcrefi为系统运行参考节点,kdroop为下垂系数。

公式(6)中Δdi4为直流侧电流和直流侧电压的方程,公式(9)表示下垂控制方式下直流侧电流和直流侧电压的关系。采用下垂控制的VSC站用公式(9)代替公式(6)中的Δdi4,非下垂控制下VSC站的潮流修正方程仍如公式(6)所示。假设直流侧有n个节点,其中m个节点采用下垂控制,其余n-m个节点采用其他控制方式。替换后的潮流修正方程的矩阵表达式如下:

ΔD′=JΔX

(10)

公式中:ΔD′=[…Δdm,1Δdm,2Δdm,3Δfm,4Δdm+1,1

Δdm+1,2ΔDdm+1,3ΔDdm+1,4…]T,J为雅可比矩阵,DX=[…ΔudiΔidiΔδiΔMi…]T。

图2 V-P下垂控制Fig.2 V-P droop control

图3 V-I下垂控制Fig.3 V-I droop control

从VSC的控制方式可得,除了控制对象为直流电压udc外,其他均为交流侧物理量,进行交直流潮流计算时,可以根据换流站的控制方式将VSC交流母线等效为PQ或PV节点进行迭代求解,方便下一步进行交直流混联系统概率潮流计算。

根据换流器的控制方式,可将交流侧和直流侧的节点进行等效,等效结果如表1所示。

表1 换流站的控制方式及节点等效Tab.1 Control methods and node equivalence of converter stations

2 交直流混联系统中的随机变量模型

针对交直流混联系统,本文提出一种基于蒙特卡罗模拟法的交直流混联系统概率潮流计算方法,待求量为各节点电压和支路功率。将系统中的随机扰动作为状态量,计算待求量的概率分布结果。由于现有交直流混联系统中的光伏输出功率和负荷需求都具有很大的不确定性,因此,首先要建立电源和负荷的概率分布模型。

2.1 光伏发电系统概率模型

由于光照强度受气象条件影响具有一定的随机性,其输出功率与光照强度密切相关,因此输出功率具有波动性和不确定性。光照强度可近似由Beta分布描述,概率密度函数为[22]

(11)

公式中:α和β为Beta分布的形状参数;r和rmax(W/m2)分别为一段时间内实际光照强度和最大光照强度;Γ为Gamma函数。RM为光电最大输出有功功率,其中RM可由下式求得:

(12)

假设有一光伏方阵,有M个光伏组件构成,每个光伏组件面积和光电转换效率分别为Am和ηm(m=1,2,…,M),可得光伏输出有功功率为

PM=rAη

(13)

公式中:A为光伏方阵总面积;η为光伏方阵的光电转换效率。

(14)

由公式(11)可得到光伏输出功率的概率函数也服从Beta分布:

(15)

公式中:RM=Ahrmax为光伏最大输出功率。

2.2 风电场概率模型

风电场的输出功率由风速的Weibull分布可以得到,Weibull分布被普遍认为是最接近风速统计描述的概率密度函数,其概率密度函数为[23]

(16)

公式中:v为风速;k和c为Weibull分布参数,k为形状参数,c为尺度参数。

其中,Weibull分布参数可由风速的平均值m和标准差s求得:

(17)

公式中:Γ为Gamma函数。

风力发电机输出功率Pw和风速v之间满足函数关系[24]为

(18)

(19)

据统计,风速大多数时间在vci和vr之间,所以,Pr和v可视为一次函数关系。因此,风机有功功率的概率密度函数为[25]

(20)

风力发电机可采用恒功率因数控制。并网风机大多为异步发电机,需要吸收无功功率,其无功功率为

Q=Ptanφ

(21)

公式中:φ为功率因数角,tanφ为负值。

2.3 负荷的概率模型

负荷的不确定性主要由负荷的随机波动引起。一般可由正态分布进行描述[26],可表示为

(22)

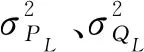
综上所述,采用蒙特卡罗模拟法求解交直流混联系统的概率潮流分布,步骤如下。

步骤1:输入基础数据(交直流混联系统数据、光伏、风电及负荷相关数据及分布状况、各个换流站控制方式和设定值);

步骤2:根据换流器的控制方式,对PCC节点进行等效。(当换流器的交流侧采用恒电压幅值控制方式时可等效为PV节点;当换流器采用恒无功功率控制方式时可等效为PQ节点);

步骤3:针对风力发电机和光伏输出功率及负荷等随机变量,采用蒙特卡罗抽样得到随机样本数据;

步骤4:进行交直流混联系统的确定性潮流计算;

步骤5:统计交直流混联系统节点电压和线路功率;

步骤6:求出系统状态变量的概率密度函数和累积分布函数。

3 算例分析

3.1 算例系统说明

本文在标准的IEEE-34节点系统[27]基础上嵌入一个三端直流网络,形成交直流混联系统,如图4所示。交流母线14、15、25通过换流器形成直流电网。换流站的各项参数、直流线路参数如表2、表3所示。系统的基准电压UB=25.64 kV,基准容量SB=1 MVA,所有的数据形式均为标幺值。

图4 修改后的IEEE-34节点测试馈线系统Fig.4 Revised IEEE-34 node test feeder system

考虑主从控制时,换流器的控制方式为:换流器1采用定直流电压控制,换流器2、3采用定功率控制,控制方式如表2所示。

表2 VSC控制参数(p.u.)Tab.2 VSC Control Parameters(p.u.)

考虑下垂控制时,换流器的控制方式为:换流器1采用电流特性下垂控制方式,换流站的参考值Idcref、Pdcref和Qsref分别为0.33、0.30和0,换流器的直流侧通过直流变压器接一个额定功率为250 kW光伏方阵。换流器2、3均采用定有功功率控制,控制方式如表2所示。

表3 直流电网线路参数(p.u.)Tab.3 DC Power Grid Line Parameters (p.u.)

为了分析分布式电源对电网的影响,本文分三种场景进行讨论:

场景1:仅考虑系统负荷随机波动的影响;

场景2:在节点34上接入1个额定功率为250 kW的光伏发电系统;

场景3:在节点34上接入1个额定功率为200 kW的风电机组和1个额定功率为250 kW的光伏发电系统。

光伏组件面积为2.16 m2,光电转换的效率为13%,额定功率为250 kW,输出功率服从Beta分布,形状参数α=0.679 9,β=1.778 7,采用恒功率因数控制,使cosj=1。风力发电机型号为丹麦Bonus 1MW/54,额定功率为200 kW,切入风速、额定风速、切出风速分别是3 m/s、14 m/s、25 m/s,风轮直径为54.2 m,输出功率出力服从Weibull分布,采用恒功率因数控制,使cosj=1。本文所用的风速和光照强度数据均由HOMER软件对我国广州地区(113°15′E,23°7′N)2020年实测数据[28]。仿真计算环境:处理器为AMD Ryzen 7 4 800U with Radeon Graphics 1.80 GHz,运行内存16.0 GB RAM,仿真软件为Matlab R2018b。

为了验证所提算法的有效性,针对交流系统,以节点电压V34和临近节点34的线路P32-34,Q32-34,直流网以换流器3的电压Vd3和直流线路Pd2-d3为例进行分析。

3.2 计算结果分析

3.2.1 状态变量的均值和标准差

1)换流器采用主从控制

当换流器采用主从控制时,直流系统不存在概率问题。因此,仅分析交流系统状态变量的概率分布状况。光伏和风电仍采用恒功率因数控制,使cosφ=1,即输出的无功功率为0,因此仅分析风电和光伏对电压和有功功率的影响。表4给出了交流系统状态变量的均值和标准差。在场景1中,仅考虑负荷波动时,电压和有功功率的标准差分别为0.002 7和0.002 1,电压和有功功率的波动很小,其中电压波动范围为(0.954,0.974);在场景2中,在光伏接入系统后,电压和有功功率的标准差分别为0.007 4和0.049 1,其中电压波动范围为(0.951,0.993),较场景1波动范围有所增大。由此可见,随着光伏和负荷的共同作用,电压和有功功率的波动性较场景1更加明显;在场景3中,分析负荷、光伏和风电对电压和有功功率的影响,在光伏接入点同时接入风电机组,组成风-光联合系统。电压和有功功率的标准差分别为0.002 9和0.008 1,其中电压波动范围为(0.954,0.977)。与场景2相比电压和有功功率波动均有明显的下降。

表4 交流系统状态变量的均值与标准差Tab.4 Mean and Standard Deviation of State Variables in the Communication System

2)换流器采用下垂控制

由表5和表6中所示的交流、直流状态变量的均值和标准差可知,由于光伏和风电均采用恒功率因数控制,使cosj=1,即输出的无功功率为0,所以,风电和光伏输出无功功率对系统状态变量波动性几乎没有影响,因此仅分析风电和光伏对电压和有功功率的影响。

交流系统计算结果分析:由表5可知,在场景1中,仅考虑负荷波动时,电压和有功功率的标准差分别为7.1×10-6和0.001 9,电压和有功功率的波动很小;在场景2中,同时考虑负荷和光伏波动对电压和有功功率的影响,电压和有功功率的标准差分别为0.004 6和0.025 8。由此可见,随着光伏的接入,电压和有功功率的波动性较场景1更加明显;在场景3中,考虑了负荷、光伏和风电对系统电压和功率的影响,在光伏接入点同时接入风电机组,组成风-光联合系统。电压和有功功率的标准差分别为0.002 9和0.008 1,与场景2相比电压和有功功率波动均有明显的下降。

直流系统计算结果分析:由表6可知,在场景1中,仅考虑负荷波动时,电压和有功功率的标准差分别为1.15×10-4和0.002 8;在场景2中,同时考虑负荷和光伏波动对电压和有功功率的影响,电压和有功功率的标准差分别为0.004 8和0.002 8。由此可见,由于光伏输出功率的波动性使得电压和功率的波动范围较场景1更大;在场景3中,考虑了负荷、光伏和风电对系统电压和功率的影响,电压和有功功率的标准差分别为5.03×10-4和1.28×10-4,与场景2相比电压和有功功率波动均有明显的下降。

综上可见,无论是交流侧还是直流侧的状态变量,风-光联合系统皆可以有效的减小新能源输出功率波动性,原因是利用了风-光联合系统中风电和光伏的互补特性。

表5 交流系统状态变量的均值与标准差Tab.5 Mean and Standard Deviation of State Variables in the Communication System

表6 直流系统状态变量的均值与标准差

3.2.2 状态变量的概率分布

1)换流器采用主从控制

表4和图5表示交流系统状态变量的概率分布状况,加入光伏后状态变量的标准差增大,状态变量的波动性有所增强。加入风电后,状态变量的波动性有所减小,其标准差有所降低。

图5为节点34电压幅值的PDF和CDF曲线,可以得到场景1在没有新能源接入时,电压的随机波动与负荷的正态分布基本一致,电压没有越限。场景2接入光伏后,节点34电压的波动范围有所增大。光伏与风电输出功率的随机性可导致节点电压波动范围增大,引起概率密度曲线畸变。由场景2和场景3电压概率分布曲线可知,风-光联合发电系统因光伏发电与风力发电互补特性,电压波动范围也更小。

表7 不同场景下节点电压的概率分布状况

表7为不同场景下稳态电压的高电压概率(Over-Voltage Probability,OVP)和低电压概率(Low-Voltage Probability,LVP)。由于三个场景的稳态电压均没有出现越限情况,在此分析稳态电压出现在高压段和低压段的概率情况。从表7可以发现,与光伏单独接入时相比,场景3(风-光联合发电系统)中电压的OVP和LVP都很小。

2)换流器采用下垂控制

如图6和图7所示的交直流侧状态变量的概率分布可知,加入光伏后系统状态变量的标准差明显提高,这就说明了新能源接入对电网有着较大冲击,不利于电网的稳定运行。而场景3与场景2相比,系统状态变量的标准差有所降低。

图6给出了节点34电压幅值的PDF和CDF曲线。从图中可以得到场景1在没有新能源接入时,电压的随机波动与负荷的正态分布基本一致,电压越限的概率为0。当场景2中接入光伏后,节点34电压有所上升且电压的波动范围有所增大;由于光伏发电和风力发电的随机性使得节点电压波动范围增大,导致概率密度曲线畸变,从图6的场景2和场景3电压概率分布曲线的变化可得到,对于风-光联合发电系统,由于光伏发电与风力发电互补,其对系统电压波动的影响相对单独光伏发电来说要小,电压波动范围也更小。

图7分别给出了直流系统状态变量的CDF图形,从直流电压的CDF曲线可以发现,风-光联合发电系统的互补作用,同样也会缩小直流系统的电压波动范围。而支路潮流变化不明显。

表8为不同场景稳态电压的OVP和LVP,仅分析稳态电压出现在高压段和低压段的概率情况。从表8可以发现,风-光联合发电系统中电压的OVP和LVP都很小,甚至于比场景1的LVP还要小。

图5 交流系统状态变量的概率分布Fig.5 Probability distribution of state variables in the communication system

表8 不同场景下节点电压的概率分布状况

综上所述,无论换流器的控制方式为主从控制还是下垂控制,新能源单独接入时会导致电压波动范围变大,体现在电压标准差、OVP和LVP增大,甚至有导致电压越限的风险。风-光联合发电系统能够有效利用风光互补作用,较新能源单独接入可以有效降低电压的标准差、OVP和LVP,从而保证了良好的电能质量。

图7 直流系统状态变量的概率分布Fig.7 Probability distribution of DC system state variables

3.2.3 新能源渗透率的影响

为了验证风-光联合系统对交直流混联电网的影响。以换流器采用下垂控制为例,在不同渗透率下对交流系统输出变量的方差进行测试,结果如表9和表10所示。

表9 光伏不同渗透率下的均值和标准差

表10 风电不同渗透率下的均值和标准差

由表9和表10可知,随着光伏渗透率由0.1到0.9,电压的标准差由0.010 8增大到0.012 1。随着风电渗透率由0.1到0.9,电压的标准差由0.010 6增大到0.013 1。因此,随着光伏和风电的渗透率增大,PCC点电压幅值波动越大,然而支路潮流的标准差受分布式电源渗透率的影响较小。

4 结 论

本文提出基于蒙特卡罗模拟的交替迭代法计算柔性交直流混联配电网的概率潮流。该方法不但可以准确分析光伏发电、风力发电以及负荷功率的不确定性,还可以计及换流器主从控制或下垂控制等控制模式。通过在修改的IEEE-34节点系统进行计算,得到以下结论。

1)通过建立光伏发电和风力发电的随机模型,应用蒙特卡罗模拟法分析分布式电源对配电系统电压质量的影响,证明分布式电源接入会使系统电压波动范围增大,从而有导致电压越限的风险。

2)针对换流器主从控制和下垂控制,建立交直流概率潮流计算模型,能较为准确得到线路的概率潮流的分布情况,具有很好的灵活性,能够为调度人员提供较好的技术支持。

3)利用分布式风-光联合系统中风电和光伏的互补特性,可以有效的减小新能源输出功率波动性,从而降低其对电力系统的冲击。

4)随着光伏渗透率和风电渗透率的增加,PCC点电压幅值波动增大,但是支路潮流的标准差基本不变。此外,通过对比三个场景可以得到,风光混合发电系统比单独的光伏发电系统能提供更好的电压质量。