应力主轴连续旋转对冻结黏土变形特性的影响

雷乐乐,王大雁,张志成,李栋伟,袁 昌

(1.东华理工大学 土木与建筑工程学院,南昌 330013;2.冻土工程国家重点实验室(中国科学院西北生态环境资源研究院),兰州 730000)

由于冰的存在,冻土中力学性质极为复杂,冻土的应力方向依赖性是指冻土的力学特性随应力方向改变而改变的性质,包含冻土的各向异性和应力主轴旋转效应两层含义。室内常规冻土三轴试验通常只能模拟应力大小的变化,无法反映主应力方向变化所带来的影响。然而,对于交通、地震荷载等施加在冻土路基上的应力或应变路径,较常规冻土三轴试验路径更复杂,其显著特征是具有明显的主应力方向变化,特别在交通荷载作用下的冻土路基,其应力主轴方向的变化甚至远比其主应力大小的变化更重要。由于路基会长期处于(纯)主应力旋转变化的作用下,引起的累积变形发展演变,势必会影响工程正常的安全运营。

冻土的总变形可分为弹性变形、塑性变形和黏性变形[1]。Tritovic[2]发现冻土的弹性模量比未冻土的大几十倍至几百倍,且受土质、温度等因素影响明显。朱元林等[3]发现冻土的应力-应变关系随应变速率的增加呈现塑性—硬化—软化的变化趋势。孙星亮等[4]发现初始切线模量受围压的影响不大,但与温度成近似线性关系,与应变速率成指数关系。马巍等[5-6]发现初始切线模量会随围压的升高而线性增大,加卸载条件下屈服强度的应力差也会随围压的增大和温度的降低而增大,但破坏时的变形几乎不发生变化,均随围压的增加而增大。徐湘田等[7]发现围压的变化会使应力-应变曲线从应变软化过渡到应变硬化。在深部冻土研究中,马巍等[5]首先提出先将试样进行固结,然后在加载状态下将其冻结,进而测定冻土力学性质。借助该试验方法,马巍等[8-11]发现初始切线模量随围压的升高而线性增大,而初始弹性模量基本不随围压的变化而发生变化;当围压较低时,冻土的破坏强度几乎不受温度变化的影响,但随围压增加,破坏强度受温度的影响程度也逐渐增大;应力-应变曲线均呈双曲线型,可分为以下3个阶段:应变随应力线性增加的弹性阶段、应变硬化阶段和屈服阶段或流动阶段;在卸载过程中,曲线类似于理想刚塑性应力-应变曲线。Li等[12]指出剪切过程中的塑性变形主要是由土体颗粒之间、土颗粒与冰颗粒之间的相互错动造成土体中孔洞形状改变造成的。Xu等[13]发现随着围压、温度的升高和压实度的降低,粉质黏土的应力-应变曲线逐渐由软化向硬化转变,随围压的增大,压实度对径向变形和破坏应变的影响逐渐消失,冻土区和未冻土区均存在这种现象。

以上研究多是基于冻土三轴试验结果,并未考虑应力主轴方向角α的影响。而在未冻土研究中发现在纯主应力轴方向连续旋转下,土体中会有塑性变形的累积,且应变的累积方向(向压应变或拉应变方向发展)和累积速度受加载应力路径影响较大[14],其主要原因是在土体中形成具有不同主应力轴方向的抗剪强度值区域。在冻土力学特性研究中,陈墩等[15-16]通过应力主轴定向剪切试验发现冻结黏土的轴向应变及剪应变均会随应力主轴方向角的不同发生改变,且应力-应变曲线形式也会由应变软化向应变硬化转变。但现有研究中考虑应力主轴方向连续变化中α加载速度及加载方向对冻土变形特性的影响还鲜有报导。为此,采用冻土空心圆柱仪,对冻结黏土开展一系列纯主应力轴单向旋转试验研究,探索应力主轴方向角旋转速度及旋转方向对冻结黏土变形特性的影响,为后续研究列车等动荷载下冻土的力学特性提供理论基础。

1 试 验

1.1 试验用土及试样制备

试验用土为青藏粉质黏土,其物理性质指标如表1所示,颗粒级配曲线如图1所示。试验中试样为重塑冻结黏土试样,干密度为1.77 g/cm3,含水率为19.8%,采用空心圆柱试样制样设备[17]进行制样,试样内直径60 mm,外直径100 mm,样高200 mm。

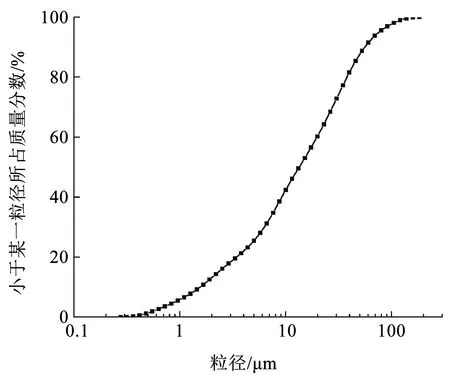
图1 土体的颗粒级配曲线

表1 试验土的物理性质指标

1.2 试验方案设计

试验采用冻土空心圆柱仪[18],应力路径设置时采用平均主应力p、中主应力系数b、最大剪应力q及应力主轴方向角α4个控制参数,表达式如式(1)所示,α为大主应力偏离竖直方向的角度。应力主轴单向旋转(以下简称单向旋转试验)过程中保持p、b、q和试验温度t不变,应力主轴正向(主应力轴方向角α从0°增加至90°)或反向旋转(α从90°减小至0°),其应力路径如图2所示。

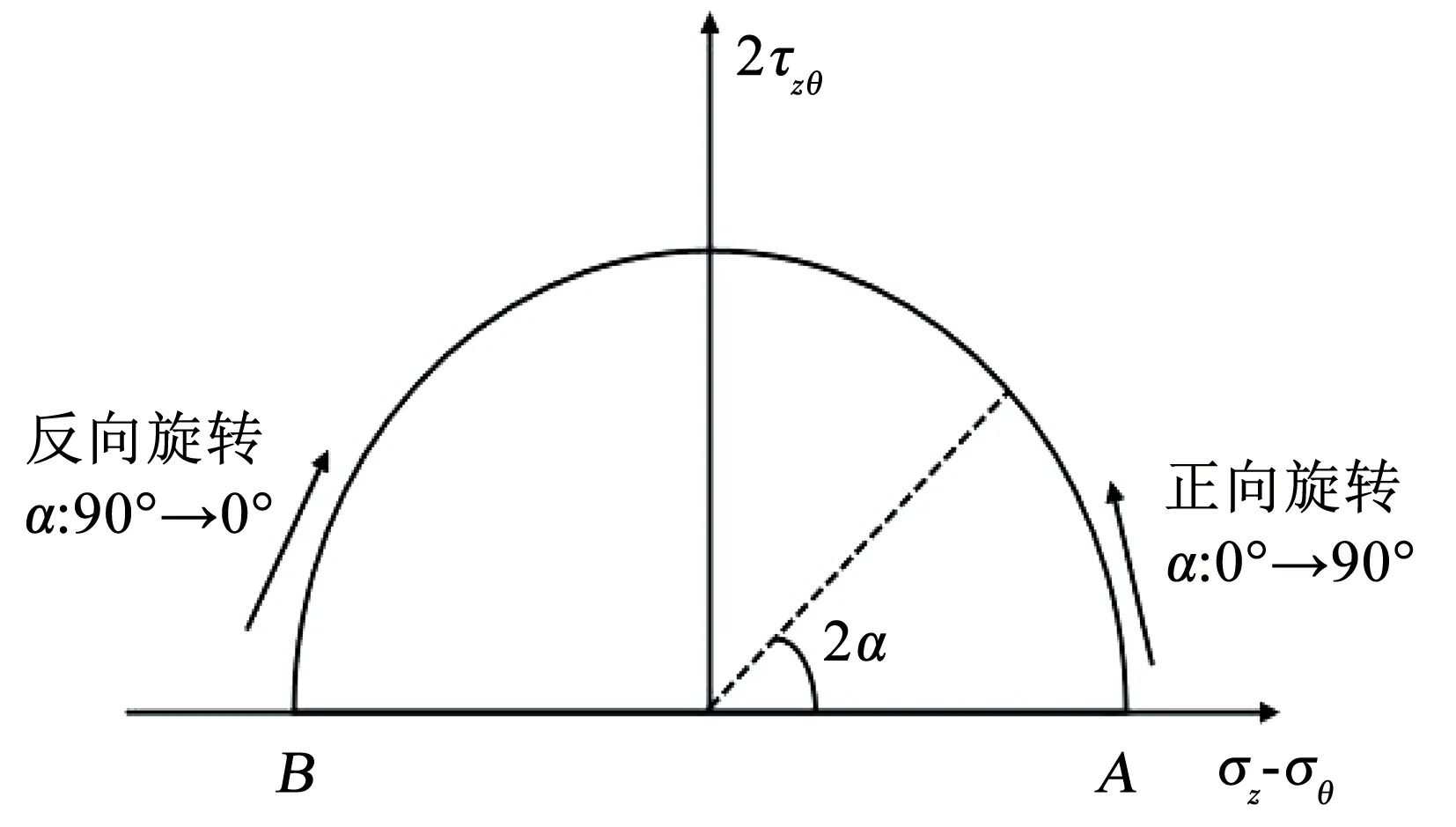
图2 单向旋转试验应力路径示意

(1)

式中:σ1、σ2、σ3分别为大、中、小主应力,σz为轴向应力,σθ为环向应力,τzθ为扭矩产生的扭剪应力。共设置两组试验,每组有两个平行试验。在不同α旋转速度试验中,为探索更大α旋转速度下冻结黏土的变形规律,在原有第1组试验(即RR1试验组)的基础上,保持其他参数不变,增加旋转速度分别为0.2、3、4、5和6 (°)/min的试验应力路径,具体参数如表2所示。

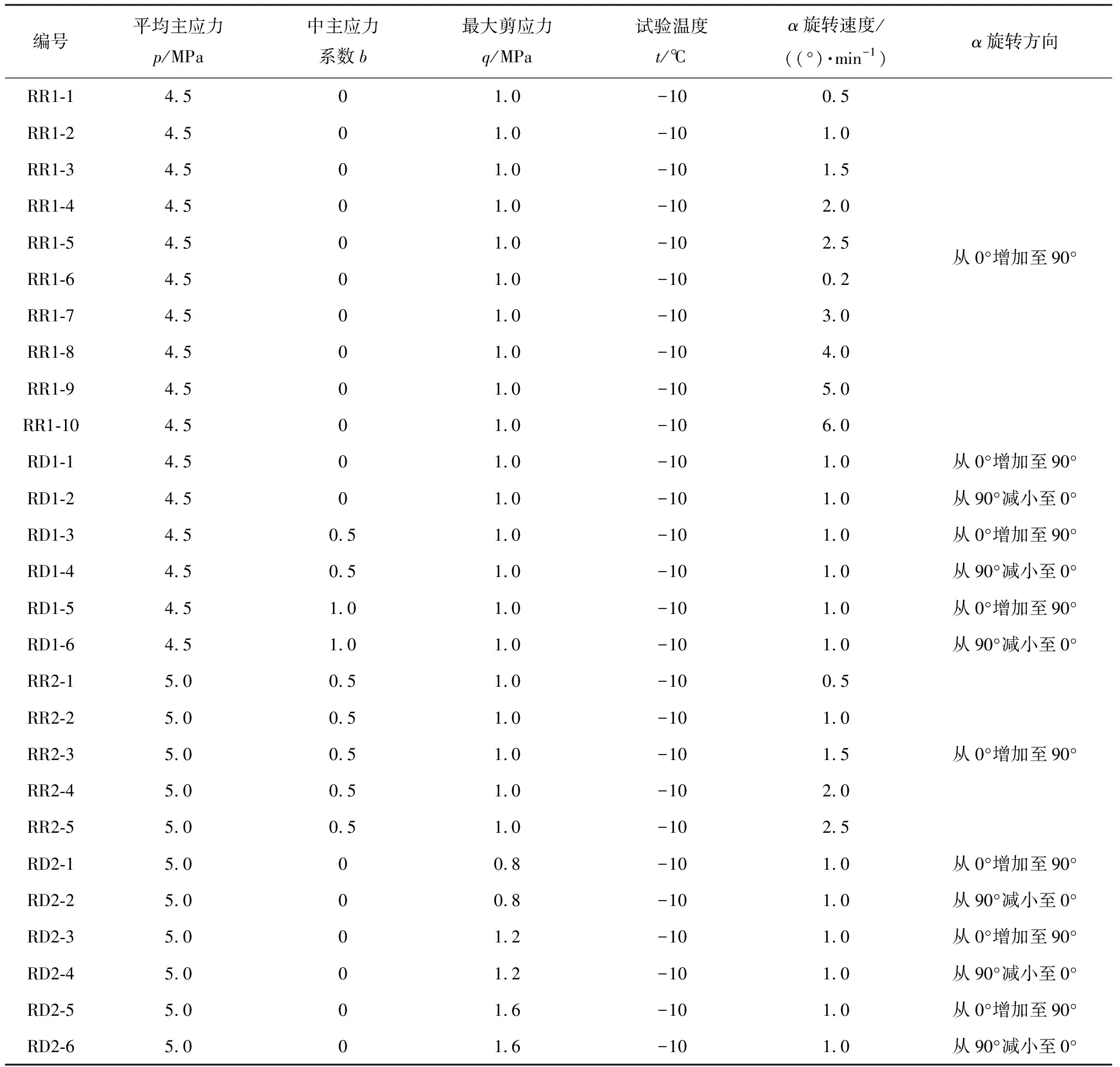
表2 单向旋转试验应力路径

2 试验结果分析

2.1 轴向变形特性

图3为不同α旋转速度时的轴向试验结果,轴向偏应力σd、轴向应变εz的表达式如下:

图3 不同α旋转速度时的轴向试验结果

(2)

式中:σz为轴向应力,p0为试验中的外部围压,uz为试样竖向位移,h0试样原始高度。从图3可以看出,当α从0°线性增加至90°时,随着轴向偏应力的减小,轴向应变先快速增加,达到峰值应变后,随着轴向偏应力的减小而缓慢减小,峰值应变滞后于峰值应力,且不同试验组中峰值应变随α的变化规律也不相同。第1组试验中,最小峰值应变出现在α的旋转速度R=1.5 (°)/min(图3(c)),说明该条件下冻结黏土的轴向抗压强度最高。之后,随α旋转速度的增加,峰值应变逐渐增加,当α旋转速度超过3 (°)/min时,峰值应变随α旋转速度的增加又减小。从图3(b)可以看出,增大p和b,单向旋转中的轴向偏应力减小,且轴向应变向负应变(即拉应变)方向发展,与文献[19]呈现相似的试验结果,但不同的是最小峰值应变出现在α旋转速度R=1 (°)/min时,说明平均主应力和中主应力也会对冻结黏土的变形有影响。

主应力轴旋转方向的不同决定了冻结黏土受力过程的不同,α正向旋转(从0°变化到90°)时,轴向为一卸载过程,反向旋转(从90°变化到0°)时,轴向为一加载过程。图4为不同α旋转方向时的轴向应力-应变曲线,其中,图4(a)为3个不同b下的结果曲线,图4(b)为3个不同q下的结果曲线,图中实心图例表示α正向旋转时的轴向偏应力-轴向应变曲线,空心图例表示反向旋转时的轴向偏应力-轴向应变曲线。

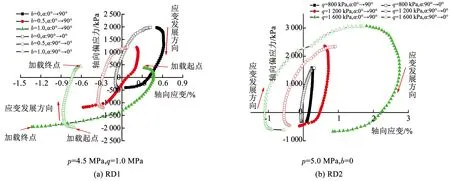
图4 不同α旋转方向时的轴向应力-轴向应变曲线

从图4可以看出,在相同应力下,由于α旋转方向不同,冻结黏土中的变形量也有明显差别,且单向旋转中形变量越大,α旋转方向对冻结黏土变形影响也越大。主要是在初始加载过程中,冻土试样受力处于相对平衡状态,要破坏该力学平衡需要较大的外力,故不论是α正向旋转还是反向旋转,初始阶段的应力-应变曲线变化速率几乎相同,但随着α的不断变化,旋转方向不同,作用在冻土上的轴向应力分量大小也有差别。当α正向旋转时,冻土试样中的轴向弹性变形逐渐恢复并向受拉方向发展,由于冻结黏土的抗拉强度远小于抗压强度,使得冻土在拉应力作用下,拉应变迅速发展;而α反向旋转时,冻土试样经历受压变形逐渐密实,抗压强度增加,当轴向偏应力未超过冻土的屈服抗压值时,即使在加载后期,轴向应变仍缓慢发展(如图4(a)所示)。一旦轴向偏应力超过冻土的屈服应力,α反向旋转时的轴向应变开始迅速发展,如图4(b)中q=1.4和1.6 MPa的试验结果所示。

2.2 剪应变特性

图5为剪应力-剪应变曲线,其中,剪应力τzθ、剪应变γzθ的表达式如下:

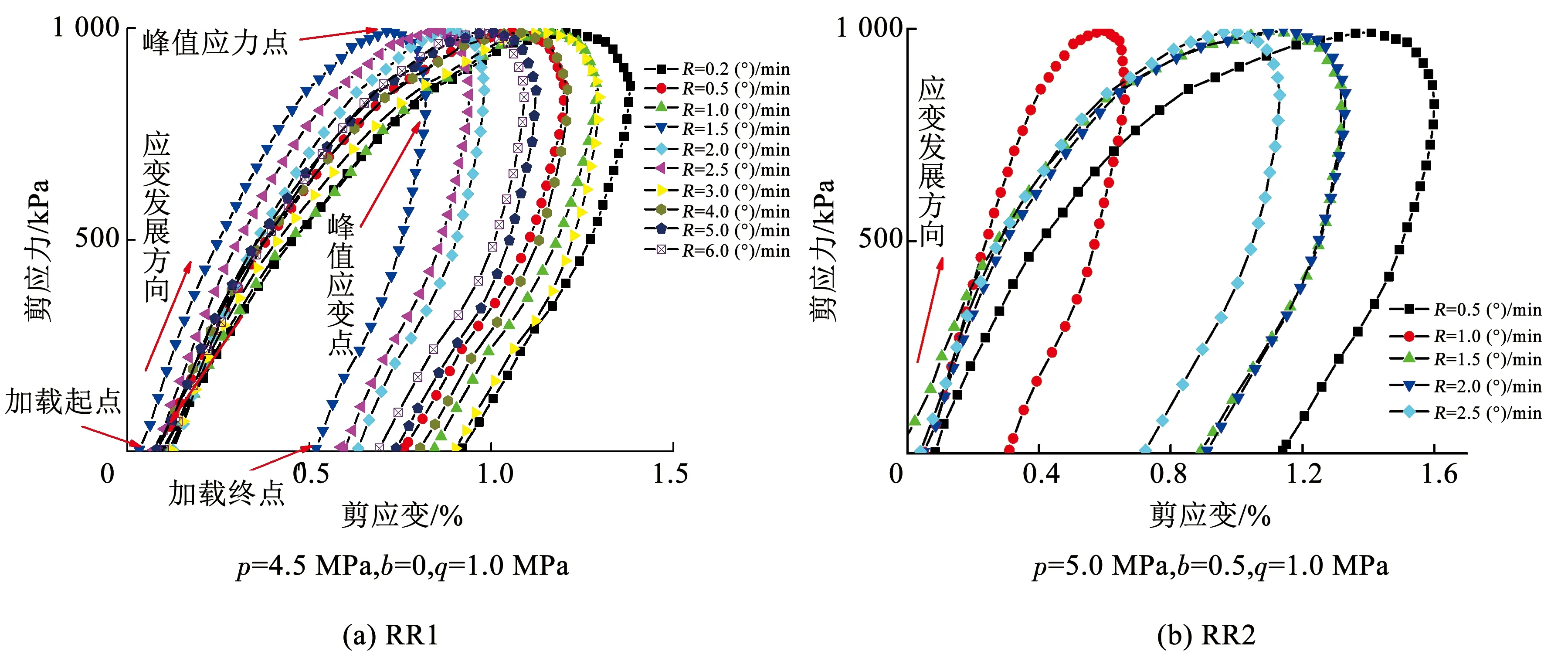
图5 不同α旋转速度时的剪应力-剪应变曲线

(3)

式中:MT为施加在试样上的扭矩,ro、ri分别为试样的外半径和内半径,θ为环向的角度位移。从图5可以看出,单向旋转中剪切变形均为加卸载过程,在α=45°时剪应力达到最大值,峰值剪应变也明显滞后于峰值剪应力。图5(a)中最小峰值剪应变也出现在α旋转速度R=1.5 (°)/min时,图5(b)中最小峰值应变出现在α旋转速度R=1 (°)/min,说明在该旋转速度下,冻结黏土能较好发挥其承载能力。从图6可以看出,在相同应力路径参数情况下,正向旋转和反向旋转过程中的剪切变形也会有较大差别。在第1组试验中,b越大,二者的剪应变差值也越大,第2组试验中q越大,二者的剪应变差值也越大。主要是由于单向旋转过程是轴向力、扭矩、内围压和外围压耦合加载过程,即使α正向旋转与反向旋转中的剪应力变化过程一样,但由于受轴向变形的影响,剪切变形在α正向旋转和反向旋转过程中也出现较大差异。

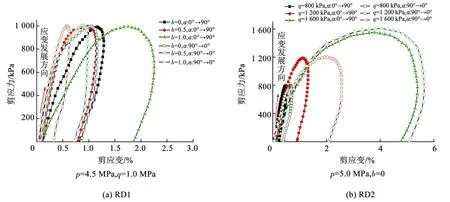
图6 不同α旋转方向时的剪应力-剪应变曲线

从图5和6还可以看出,加载结束时,剪应力减小至0应力,而剪应变均不为0,说明经历单向旋转后,冻结黏土中产生了一定的塑性剪切变形。图7和8分别为不同α旋转速度和旋转方向下的塑性剪应变变化曲线。

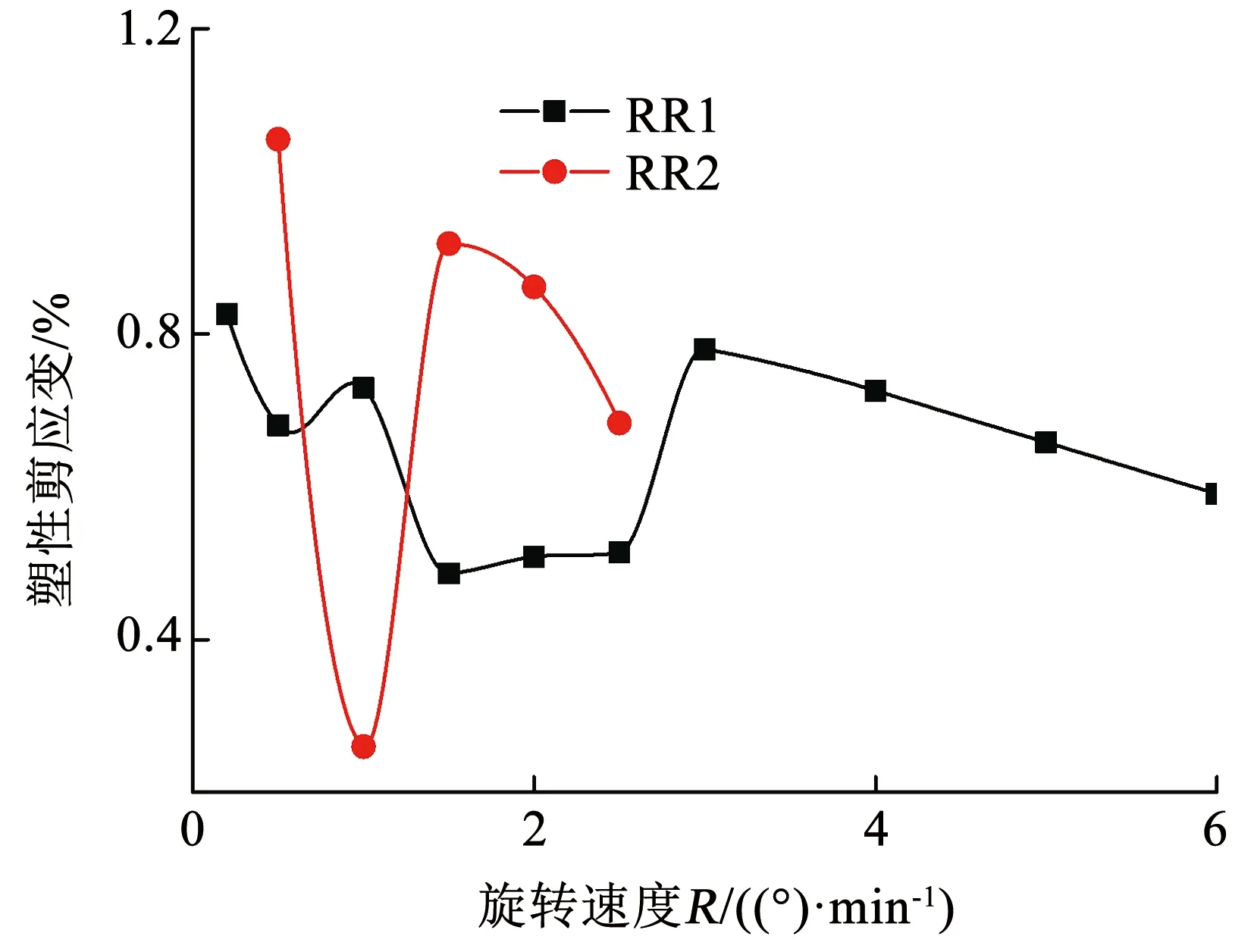
图7 塑性剪应变随α旋转速度变化曲线

从图7可以看出,塑性剪应变随着α旋转速度的增加先减小后增加,当旋转速度较大后,又随着旋转速度的增加而减小,α旋转速度较小(如R=0.2 (°)/min)或较大(如R=3 (°)/min)均会在冻土试样中产生较大的塑性剪应变,其主要原因为旋转速度的不同会改变加载时间。当α旋转速度较小时,加载时间增长,冻土的变形主要为蠕变变形,而α旋转速度较大,加载时间相对较短,冻土的变形主要为瞬时变形,表现为冻土的瞬时强度。当α旋转速度进一步增加,由于冻结黏土的黏塑性变形特性,应变发展滞后于应力发展(图3～6),应力作用下冻土还未来得及发生变形,故旋转结束时的塑性剪应变也较小。从图7还可以看出,应力路径应力参数的变化会使α旋转速度对塑性剪应变的影响程度发生改变,但当α旋转速度较小时,仍会在冻结黏土中产生较大的塑性剪应变。

从图8可以看出,旋转方向不同,冻结黏土中的塑性剪应变也不相同,随着单向旋转中b的增大,正向旋转和反向旋转中的塑性剪应变差逐渐增加,随着q的增加,二者的差先增加后减小,主要是当q越大,单向旋转中的剪应力也越大(图6(a)),一旦超过冻结黏土的屈服剪应力,塑性剪应变将迅速发展,使得旋转方向对不同q下的塑性剪应变影响较大。

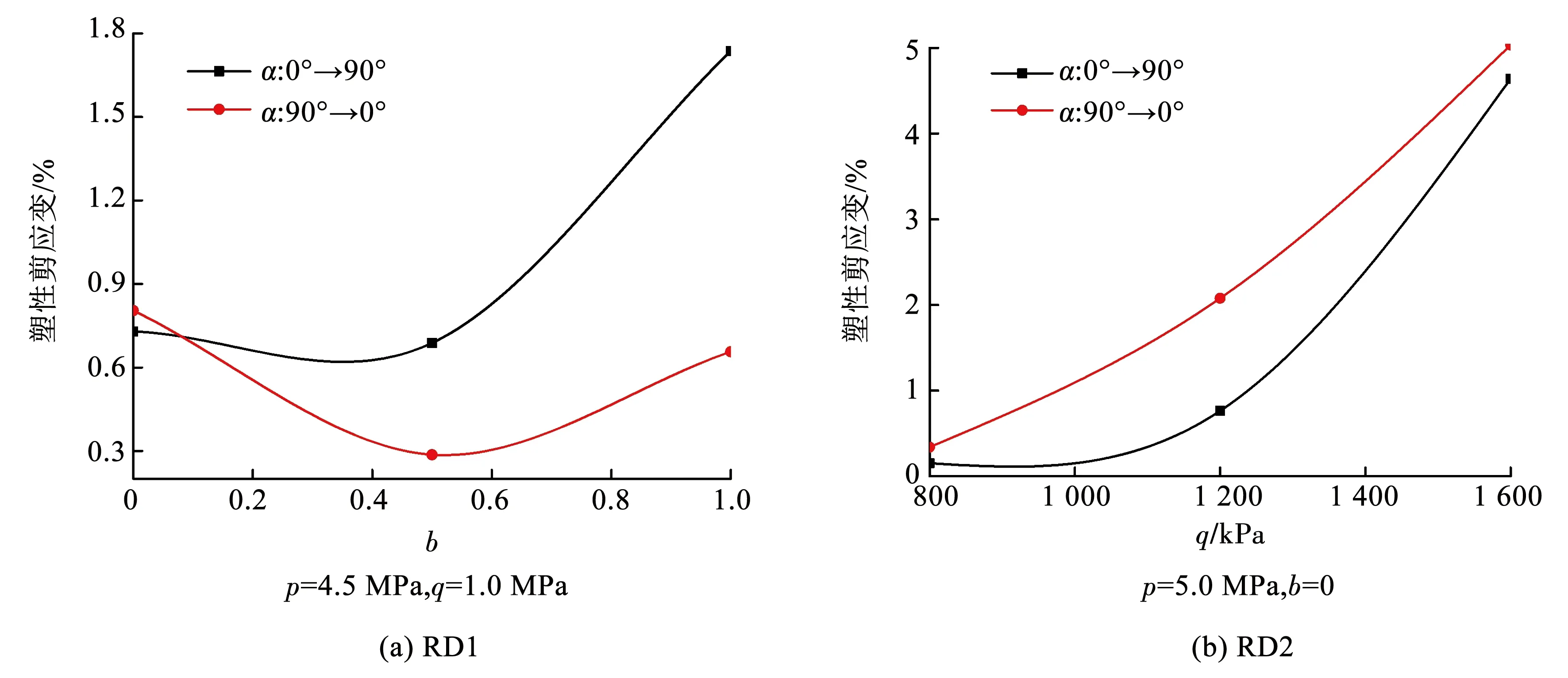
图8 塑性剪应变随α旋转方向变化曲线

3 滞回曲线特性

滞回曲线是描述一个周期荷载作用下材料的应力-应变关系,其形态特征包含材料的变形、刚度变化及能量耗散等信息。从图6可以看出,在单向旋转中,剪应力-剪应变曲线存在滞回圈。采用滞回圈端点An和底边中点Bn的应力差与其应变差的比值k表示滞回圈的倾斜程度,如图9所示,其反映了土体的刚度和弹性性能。

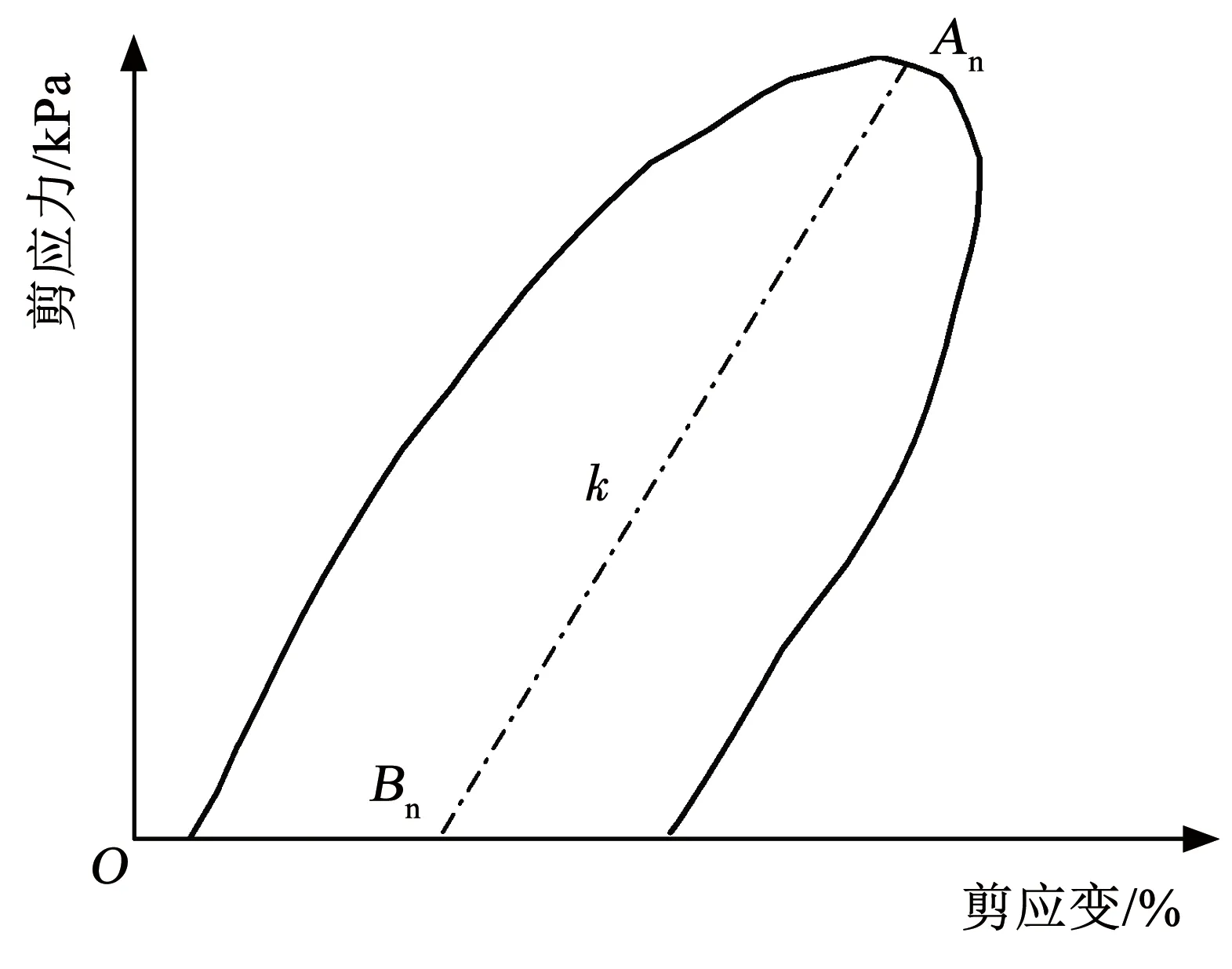
图9 滞回圈形态参数k的定义

从图10可以看出,随着α旋转速度的增加,冻结黏土的强度先快速增加,达到峰值后又缓慢减小,最终趋于稳定。说明当α旋转速度较小时,会对冻结黏土的强度有较大影响,但当α旋转速率较大时,对冻结黏土强度的影响较小。因此,对于冻土路基,应限制路基上方的车辆行驶速度,使之保持在一定的行驶速度下,可有效降低车辆荷载对冻土路基强度的影响。从图11可以看出,不同中主应力系数b条件下,正向旋转和反向旋转时的k值曲线形式相似,均在b=0.5时达到最大k值,但反向旋转时冻结黏土的强度要高于正向旋转时。在第2组试验中,正向旋转冻结黏土强度随q增加近似呈线性降低,而反向旋转时冻结黏土强度随q增加先快速降低,当q超过1.2 MPa后,强度降低的速度明显减缓。因此,如不考虑荷载加载方向(即形变矢量)的影响,所得的本构模型不能很好地预测冻土实际的变形发展规律。

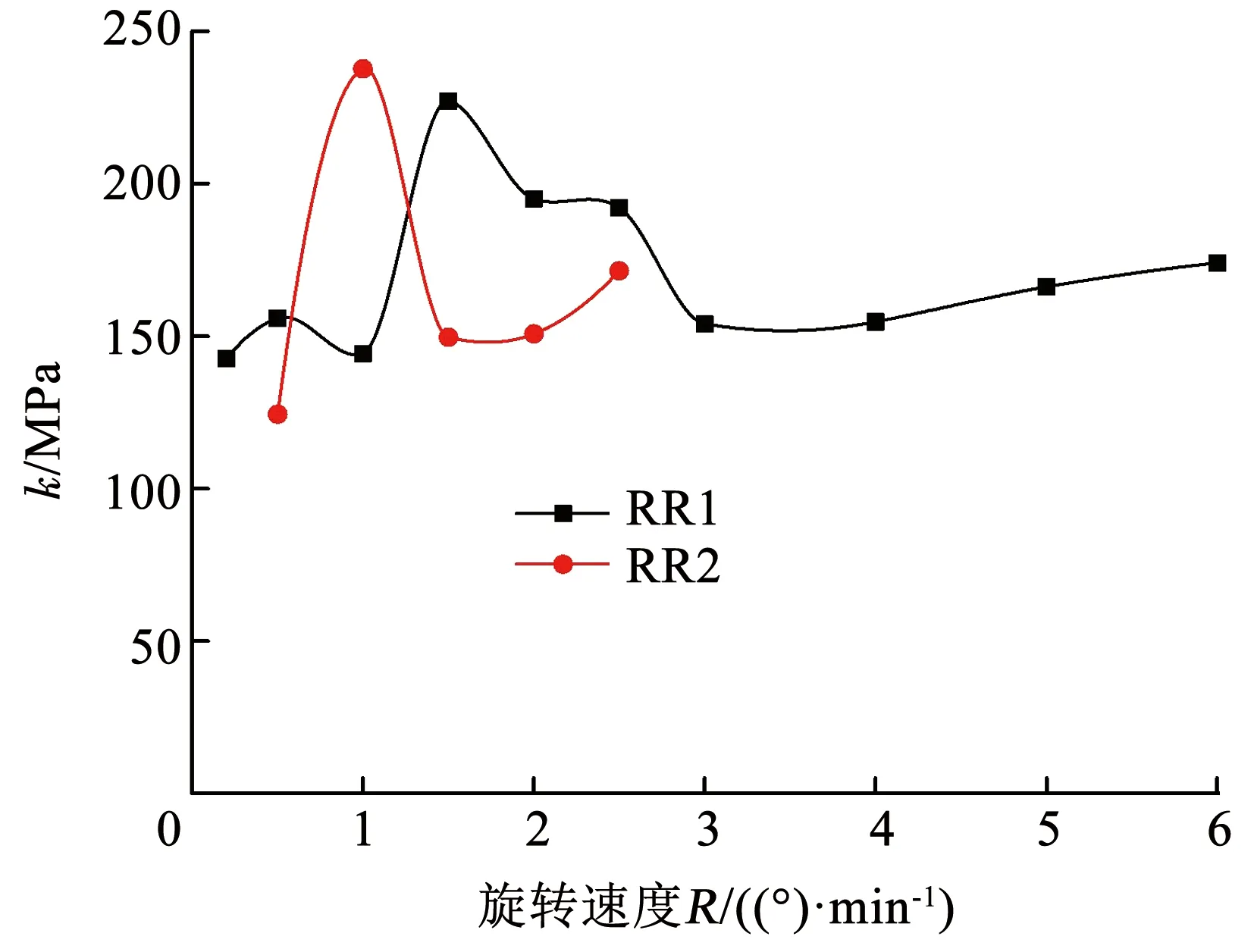
图10 不同α旋转速度时的k值曲线

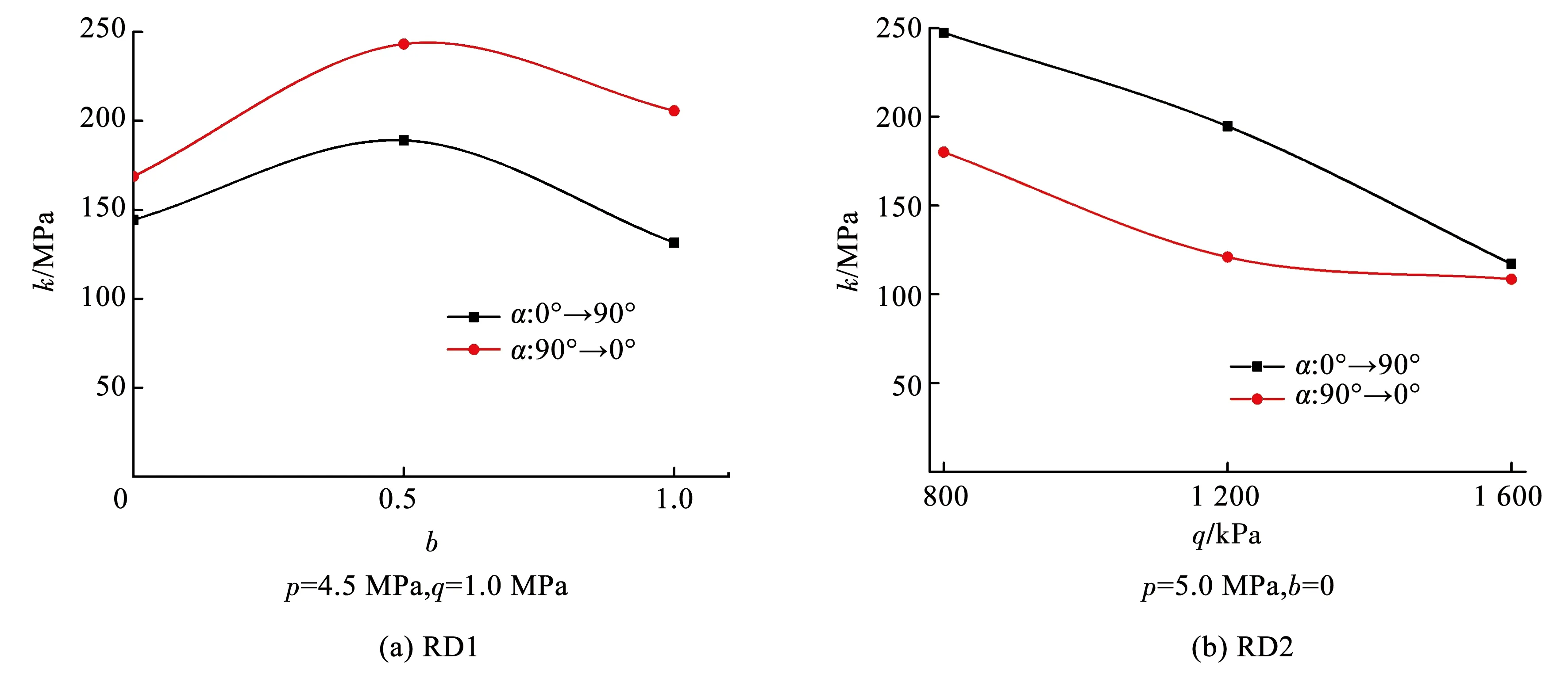
图11 不同α旋转方向时的k值曲线

4 结 论

1)峰值应变滞后于峰值应力,即使不改变应力幅值的大小,纯应力主轴旋转过程中也会在冻结黏土中产生塑性应变。

2)应力主轴方向角α旋转速度均会对冻结黏土的轴向变形和剪切变形有影响,且存在一临界α旋转速度,在该条件下,冻结黏土可较好发挥其承载性能。α旋转方向不同,冻结黏土中的变形量也有明显差别,且单向旋转中变形量越大,α旋转方向对冻结黏土变形影响也越大。

3)经历单向旋转后,冻结黏土中会产生塑性剪切变形,塑性剪应变随着α旋转速度的增加先减小后增加,当旋转速度较大后,又随着旋转速度的增加而减小;α旋转速度较小或α旋转速度较大均会在冻土试样中产生较大的塑性剪应变。α旋转方向不同,单向旋转中产生的塑性剪应变也有差别,正向旋转和反向旋转中的塑性剪应变差值与冻结黏土的受力过程密切相关。

4)滞回曲线特性分析可知,随着α旋转速度的增加,冻结黏土的强度先快速增加,达到峰值后又缓慢减小,最终趋于稳定;旋转方向不同时,中主应力系数b变化不会对冻结黏土强度变化规律产生较大影响,但是会影响正向旋转和反向旋转时的强度值;而最大剪应力q变化对冻结黏土的强度变化规律和强度值均有影响。