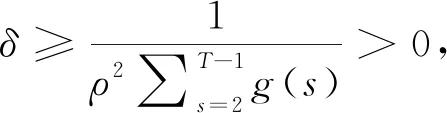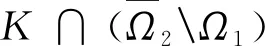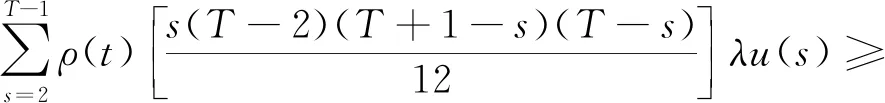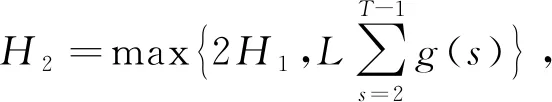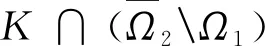一类非线性四阶离散边值问题正解的存在性

赵亚丽,陈天兰

(西北师范大学数学与统计学院,甘肃 兰州 730070)

令T≥4为一整数.记

T0={0,1,…,T+1},

T1={1,2,…,T},

T2={2,3,…,T-1}.

离散边值问题由于其重要的理论价值和物理背景,一直受许多研究者所关注,并获得了丰富的研究成果[1-11].众所周知,弹性梁方程在工程中有着不可或缺的作用,近年来,对两端简单支撑的非线性四阶离散边值问题解的存在性和多重性研究已有大量结果[2-3,6-7],其中大多数结果是基于锥上的不动点定理、不动点指数理论和拓扑度理论等.

He等[3]运用锥上的不动点定理研究了非线性四阶离散边值问题

Δ4u(t-2) -λa(t)f(u(t))=0,

t∈{2,3,…,T+2},

u(0)=u(T+2)=Δ2u(0)=Δ2u(T)=0

正解的存在性,其中λ是特征值,权函数a:{1,2,…,T+1}→[0,∞),f:R+→R+连续且T≥1.

Ma等[4]运用不动点指数理论研究了非线性四阶离散边值问题

Δ4u(t-2)-λf(t,u(t))=0,

t∈{2,3,…,T},

u(1)=u(T+1)=Δ2u(0)=Δ2u(T)=0

正解的存在性和多解性,其中λ>0是参数,f:T2×[0,∞)→[0,∞)连续且T≥5.然而,关于非线性四阶离散边值问题

Δ4u(t-2)+f(u(t))=0,t∈T2,

(1)

u(0)=Δu(0)=Δu(T)=Δ2u(0)=0

(2)

正解存在性从未被研究,其中f:[0,∞)→[0,∞)连续.事实上,在首次建立其相应线性问题的格林函数时带来了极大的挑战性,进而在讨论其性质时,又是一项非常艰巨的任务,因此,对该类问题的研究是非常有必要和有意义的.

为此,本文运用锥上的不动点定理获得了非线性四阶离散问题(1)～(2)正解的存在性.

本文总假定:

(Hf)f:[0,∞)→[0,∞)连续.

记

则f0=0且f∞=∞对应超线性情形,f0=∞且f∞=0对应次线性情形.

本文的主要结果如下:

定理1假定(Hf)成立且f满足:

f0=0且f∞=∞.

则问题(1)～(2)至少存在一个正解.

定理2假定(Hf)成立且f满足:

f0=∞且f∞=0.

则问题(1)～(2)至少存在一个正解.

1 预备知识

本文使用的主要工具是:

满足:

(i) ‖Au‖≤‖u‖,u∈K∩∂Ω1且‖Au‖≥‖u‖,u∈K∩∂Ω2或

(ii) ‖Au‖≥‖u‖,u∈K∩∂Ω1且‖Au‖≤‖u‖,u∈K∩∂Ω2,

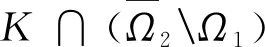
引理2设h:T2→R.则四阶线性边值问题

Δ4u(t-2)+h(t)=0,t∈T2,

u(0)=Δu(0)=Δu(T)=Δ2u(0)=0

(3)

等价于

(4)

其中

证明设u满足式(3),则通过对式(3)中的方程进行一系列和分运算,结合u(0)=Δu(0)=Δ2u(0)=0可得,

(5)

代入边界条件Δu(T)=0,有

进而解得

(6)

将式(6)代入式(5)中可得,

T(T-1)(t-s)(t-s-1)(t-s+1)]·

[6T(T-1)]-1h(s)+

因此,u也满足式(4).

另一方面,很容易验证式(4)满足式(3).

引理3格林函数G(t,s)满足如下性质:

(i)G(t,s)≥0,s,t∈T1.

(ii)ρ(t)Φ(s)≤G(t,s)≤Φ(s),s,t∈T1.其中

证明(i) 当1≤t≤s≤T-1时,显然,G(t,s)≥0.

当2≤s≤t≤T时,下面分两种情况讨论.当t-s-1≤0时,显然G(t,s)≥0;当t-s-1>0时,即t>s+1,有

G(t,s)=[t(t-1)(t-2)(T+1-s)(T-s)-

T(T-1)(t-s)(t-s-1)(t-s+1)][6T(T-

1)]-1>{(t-3)[t(t-1)(T+1-s)(T-s)-

T(T-1)(t-s)(t-s+1)]}[6T(T-1)]-1=

{(t-3)[(t2-t)(T2-2Ts+s2+T-s)-

(T2-T)(t2-2ts+s2+t-s)]}[6T(T-1)]-1=

{(t-3)[s2(t2-T2)+s2(T-t)+2stT(T-t)+

s(T2-t2)+s(t-T)+2tT(t-T)]}[6T(T-

1)]-1={(t-3)(T-t)[s2(1-T-t)+

s(2tT+T+t-1)-2tT]}[6T(T-1)]-1=

{(t-3)(s-1)(T-t)[2tT-s(T+t-1)]}

[6T(T-1)]-1>{(t-3)(s-1)(T-t)[2(s+

1)T-sT-st+s]}[6T(T-1)]-1=

{(t-3)(s-1)(T-t)[s(T-t)+2T+s]}

[6T(T-1)]-1≥0.

(7)

故(i)成立.

(ii) 当1≤t≤s≤T-1时,有

另一方面,

当2≤s≤t≤T时,有

G(t,s)=[t(t-1)(t-2)(T+1-s)(T-s)-

T(T-1)(t-s)(t-s-1)(t-s+1)][6T(T-

另一方面,同式(7)的处理方法,则

G(t,s)=[t(t-1)(t-2)(T+1-s)(T-s)-

T(T-1)(t-s)(t-s-1)(t-s+1)][6T(T-

1)]-1>{(t-2)[t(t-1)(T+1-s)(T-s)-

T(T-1)(t-s)(t-s+1)]}[6T(T-1)]-1=

{(t-2)(s-1)(T-t)[2tT-s(T+t-1)]}·

[6T(T-1)]-1≥

[(t-2)(T-t)(T-t+1)s(T-2)(T+1-

s)(T-s)][12T(T-1)3(T-3)]-1.

故(ii)成立.

引理4设h:T2→[0,∞).则问题(3)的唯一解u非负,且满足

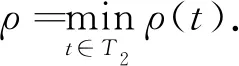
证明由引理2和引理3可知,u(t)非负,且对任意t∈T1,有

进而得到,

另一方面,

ρ(t)‖u‖≥ρ‖u‖.

下面引入本文使用的空间:

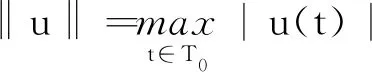
定义非线性算子A:K→E,

依据引理2,很容易得到如下结论成立.

引理5若(Hf)成立,则u(t)是问题(1)～(2)的正解当且仅当Au=u.

引理6若(Hf)成立,则算子A:K→K全连续且A(K)⊂K.

证明由引理4可知,A(K)⊂K.由Arzel-Ascoli定理可知,A:K→K是全连续的.

2 主要结果的证明

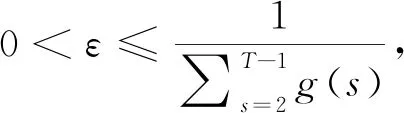
Ω1={u∈E:‖u‖

则对任意u∈K∩∂Ω1,t∈T1,由引理3可得,

(8)

其中

因此,

‖Au‖≤‖u‖,u∈K∩∂Ω1.

Ω2={u∈E:‖u‖

则对任意u∈K∩∂Ω2,t∈T2,由引理4可得,

由引理3和引理4可得,

因此,

‖Au‖≥‖u‖,u∈K∩∂Ω2.

Ω1={u∈E:‖u‖

则对任意u∈K∩∂Ω1,t∈T2,由引理3和引理4可得,

‖u‖.

因此,

‖Au‖≥‖u‖,u∈K∩∂Ω1.

下面分两种情况考虑.

(i) 若f有界.即存在L>0,对任意u∈[0,∞),有f(u)≤L.记

Ω2={u∈E:‖u‖

则对任意u∈K∩∂Ω2,t∈T1,由式(8)可得,

因此,

‖Au‖≤‖u‖,u∈K∩∂Ω2.

若u∈K∩∂Ω2,则有f(u)≤ηH2.由式(8)可得,

因此,

‖Au‖≤‖u‖,u∈K∩∂Ω2.