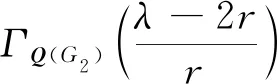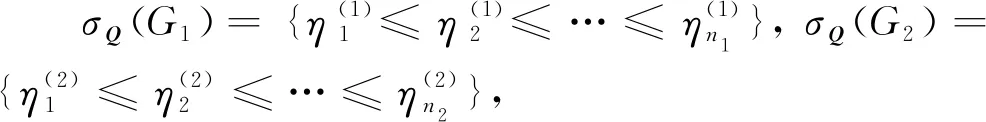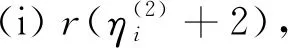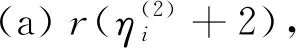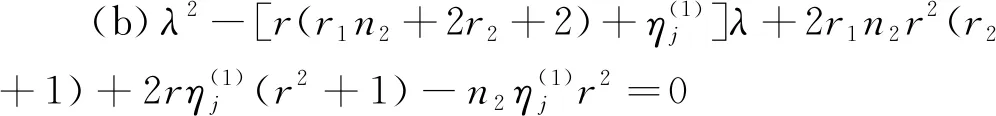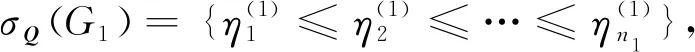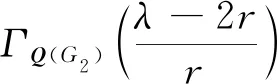赋权边冠图的广义谱
于 祥,马小玲
(新疆大学数学与系统科学学院,新疆 乌鲁木齐 830046)
许多社会、生物和通信系统都可以由网络很好地描述,其中顶点代表了系统的元素,边代表元素之间的相互作用.近年来,对网络的研究已经成为学者们重点关注的对象[1].事实上,上面提到的各种网络大多是未赋权的,它们的边权重可以看成是单位权重,但这样只考虑了顶点的分布和它们之间的关系,可能忽略了很多顶点之间其他的信息.而赋权网络可以更好地表示现实世界的系统,因为权重在分析某些网络属性时至关重要.因此,近些年来,关于构造赋权网络的问题在很多领域都有研究,也引起了许多研究人员的关注[2-4].
两个图的点冠运算首先由Frucht等[5]引入,其目的是构造一类图,使其自同构群是两个自同构群的织积(wreath product).接着,McLeman等[6]定义了矩阵的一个新的不变量——M冠,并用它来计算两个图的点冠运算后得到的新图的邻接谱,表明了该谱是可以由原来的两个图的谱以及对应图矩阵的M冠表示.2010年,Hou等[7]给出了图的边冠运算的定义,并从特征向量的角度得到了两个图的边冠运算后得到的新图的邻接谱.2016年,Cui等[8]通过矩阵计算给出了关于图做点冠和边冠运算的新图的无符号拉普拉斯谱.2014年,Liu[9]对两个图的点冠和边冠运算的拉普拉斯谱进行了研究.2017年,Chen等[10]研究了两个图做点冠和边冠运算后的新图的规范化拉普拉斯谱.近几年,学者们将目光转向了两个图的赋权点冠和赋权边冠图的谱问题研究,Dai等[11]研究了赋权点冠图的邻接谱和拉普拉斯谱.Mahanta等[12]和Liu等[13]则分别给出了赋权边冠图的广义谱.基于以上理论和结果,本文采用不同的方法研究了赋权边冠图的邻接谱、拉普拉斯谱和无符号拉普拉斯谱,同时,应用这些结果,进一步考虑了赋权边冠图的基尔霍夫指标和生成树的个数问题.

L(G)=D(G)-A(G),Q(G)=D(G)+A(G).
根据Q(G)和R(G)的定义,很容易可以得到Q(G)=R(G)R(G)T,RT是矩阵R的转置矩阵.特别地,若图G是一个k-正则图,则:
L(G)=D(G)-A(G)=kIn-A(G),
Q(G)=D(G)+A(G)=kIn+A(G).
设G1和G2分别是具有n1和n2个顶点,m1和m2条边的两个图.G1和G2的边冠运算定义为G1的每一条边对应一个G2,然后将G1的每一条边的两个端点与其对应的G2的每个顶点相连.G1和G2的边冠图G1◇G2有n1+m1n2个顶点.在G1和G2的边冠运算的基础上,Liu等[13]定义了赋权边冠图,设图G1和G2都是简单无向图,G1和G2先做边冠运算得到新图G1◇G2,然后给新图中的每条边都赋一个加权因子r,其中0 图1 C4,K3及r权边冠图C4◇K3Fig.1 C4,K3 and r-weighted edge corona graph C4◇K3 在本节中介绍一些有用的结果和概念,这些结果和概念对得到主要结论起到了重要作用.本文中,Ik表示k阶单位矩阵,1k为k阶全1列向量. 设A=(aij)m×n和B=(bij)p×q是两个矩阵,则A和B的Kronecker积为一个mp×nq矩阵A⊗B,即将A中的每个元素aij用aijB代替所得到的矩阵[14].关于Kronecker积有以下性质: (A⊗B)(C⊗D)=AC⊗BD, (A⊗B)T=AT⊗BT, A⊗(B+C)=A⊗B+A⊗C, 其中,AT是矩阵A的转置矩阵. 引理1[15]设M1,M2,M3,M4分别是p×p,p×q,q×p,q×q阶矩阵.如果M4是可逆矩阵,则 设M是一个n×n阶的矩阵,矩阵M的冠记为ΓM(λ),被定义为矩阵(λIn-M)-1中所有元素的和[5],即 对于函数ΓM(λ),显然变量λ出现在其分子和分母中.在这种情况下,称使分母为零的λ值是该函数的极点. 引理2[8]如果M是一个n×n阶矩阵,并且M的每一行的和都等于常数s,则 引理3[8]若图G是一个完全二部图Kp,q,A(G)为其邻接矩阵,Q(G)是无符号拉普拉斯矩阵,则 引理4[16]设G是n个点的连通图,R(G)是图G的关联矩阵.若图G是二部图,则rank(R(G))=n-1,否则rank(R(G))=n. 引理5[16]设图G是谱半径为ρ的连通图,-ρ也是G的特征值当且仅当图G是二部图. 引理6令G是有n个点的连通图,设图G的拉普拉斯谱为{0=μ1<μ2≤…≤μn},则: (i) 图G的基尔霍夫指标为[18] (ii) 图G的生成树的数目τ(G)[19]为 对于i=1,2,设Gi是有ni个点,mi条边的图,G1是r1正则图,A(Gi)是图Gi的邻接矩阵,R(Gi)是Gi的关联矩阵.根据赋权边冠图的定义,对G的顶点集V(G)进行划分,得到如下互不相交的顶点集V1,U1,U2,…,Um1,使得V=V1∪U1∪U2∪…∪Um1,其中V1是G1的顶点,Ui是图G1的第i条边对应的G2的顶点(i=1,2,…,m1).因此,r权边冠图G=G1◇G2的广义邻接矩阵和度矩阵如下: (1) D(G)= (2) fA(G)(λ)= 证明根据r权边冠图的邻接矩阵的表达式(1),应用引理1有 fA(G)(λ)=det(λIn1+m1n2-A(G))= det(Im1⊗(λIn2-rA(G2)))detB= 应用Kronecker积的性质,得到以下等式 [Im1⊗(λIn2-rA(G2))]-1[R(G1)T⊗1n2]}= 定理1得证. 若G2是正则图或者完全二部图时,通过定理1,可以得到r权边冠图G1◇G2的广义邻接谱,推论1和2给出了其特征值的准确表达式. 从图3(a)计算可知,随MgO厚度增加(0,0.5,1.0,1.5 nm),器件Rs分别为4.1,3.4,1.8和2.7 Ω/cm2.即随着MgO厚度的增加,Rs先降低,这可通过MgO介质层引起的Al/Si肖特基势垒降低来解释;但是随着MgO厚度的进一步增大,Gr/Si电池的串联电阻将重新增加. (iii)rr2,重数为m1-n1. 证明因为G2是r2-正则图,则A(G2)的行和都等于r2.根据引理2,可得 (3) 其中j=1,2,…,n1. 接下来考虑当G1是正则图,G2是完全二部图Kp,q的情况. (i) 0,重数为m1(n2-2); 证明因为G2=Kp,q,则由引理3可知 (4) 设G1是有n1个点,m1条边的r1-正则图,G2是有n2个点,m2条边的任意图.令L(G1)和L(G2)分别是图G1和G2的拉普拉斯矩阵,R(G1)是G1的关联矩阵.因为L(G)=D(G)-A(G),所以由方程(1)和(2),可知r权边冠图G=G1◇G2的广义拉普拉斯矩阵如下: L(G)= (iii) 2r,重数为m1-n1. 图2 广义拉普拉斯矩阵的特征向量的表示Fig.2 Representation of generalized Laplacian eigenvectors 因此,对于实数pi(i=1,2,…,n1)和a,有 (5) 通过解方程组(5),可得 (6) 设z1,z2,…,zt是R(G1)z=0的基础解系,那么有[图2(c)] 下面给出r权边冠图G=G1◇G2的广义拉普拉斯谱的一个应用. (i) 图G的基尔霍夫指标为 (ii) 图G的生成树数目τ(G)为 由引理6(i)可知,图G的基尔霍夫指标为 同理,由引理6(ii)可知,图G的生成树的数目为 设G1是有n1个点,m1条边的r1-正则图,G2是有n2个点,m2条边的任意图.令Q(G1)和Q(G2)分别是图G1和G2的无符号拉普拉斯矩阵,R(G1)是G1的关联矩阵.因为Q(G)=A(G)+D(G),所以根据方程(1)和(2),有r权边冠图G=G1◇G2的广义无符号拉普拉斯矩阵为 Q(G)= (7) 接下来先给出r权边冠图G=G1◇G2的无符号拉普拉斯特征多项式的表达式,如定理4. 证明根据r权边冠图G的无符号拉普拉斯矩阵的表达式(7),应用Schur补引理1,可知r权边冠图G的无符号拉普拉斯矩阵的特征多项式如下: fQ(λ)=det(λIn1+m1n2-Q(G))= det(Im1⊗((λ-2r)In2-rQ(G2))det(C))= det(C)=det{(λ-rr1n2)In1-Q(G1)- rQ(G2))]-1(R(G1)T⊗1n2)}= det{(λ-rr1n2)In1-Q(G1)- 因此,定理4得证. 设G1是正则图,若G2是正则图或者完全二部图,通过定理4,可以得到r权边冠图G1◇G2的广义无符号拉普拉斯谱.推论3和4给出了其对应的r权边冠图的无符号拉普拉斯谱的准确表达式. (iii) 2r(r2+1),重数为m1-n1. 证明因为G2是r2-正则图,所以G2的无符号拉普拉斯矩阵Q(G2)的行和都等于2r2.因此,由引理2可知 以上得到了Q(G)的m1(n2-1)+2n1个特征值.类似于推论1的证明,其余的m1-n1个特征值是2r(r2+1). 下面考虑G1是正则图,G2是一个完全二部图Kp,q的情况. (i)r(p+2),重数是m1(q-1); (ii)r(q+2),重数为m1(p-1); (iv) 2r和r(n2+2),重数都是m1-n1. 证明因为G2=Kp,q,所以由引理3,可得 (a)r(p+2)的重数是m1(q-1); (b)r(q+2)的重数为m1(p-1); 类似于推论2的证明,Q(G)的其余特征值为极点2r和r(n2+2),并且2r和r(n2+2)的重数都是m1-n1. 图3 K3,K2及赋权边冠图K3◇K2Fig.3 K3,K2 and weighted edge corona graph K3◇K2 A(G)= 利用数学软件MATLAB求解广义邻接矩阵A(G),拉普拉斯矩阵L(G)=D(G)-A(G)和无符号拉普拉斯矩阵Q(G)=D(G)+A(G)的特征值,可以得到如下结论: 图G的广义邻接谱: {-1.280 8[2],-0.5[3],-0.350 8,0.780 8[2], 2.850 8}; 拉普拉斯谱: {0,0.878 7[2],2[3],3,5.121 3[2]}; 无符号拉普拉斯谱: {1[3],1.550 5,1.634 0[2],3.366 0[2],6.449 5}. 另一方面,已知图G1和G2的邻接谱分别为σA(G1)={(-1)[2],2},σA(G2)={-1,1}.通过推论1,有: G的广义邻接谱为{-1.280 8[2],-0.5[3],-0.350 8,0.780 8[2],2.850 8}. 注意到图G1和G2的拉普拉斯谱分别为σL(G1)={0,3[2]},σL(G2)={0,2}.由定理2可得: G的广义拉普拉斯谱为{0,0.878 7[2],2[3],3,5.121 3[2]. 已知图G1和G2的无符号拉普拉斯谱是σQ(G1)={1[2],4},σQ(G2)={0,2},利用推论3有: σQ(G)={1[3],1.550 5,1.634 0[2],3.366 0[2],6.449 5}. 因此,通过上述例子可以发现,本文主要结论对于考虑r权边冠图的谱是行之有效、并且简捷方便的.
1 准备工作
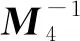
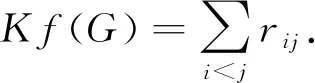
2 赋权边冠图G=G1◇G2的广义邻接谱
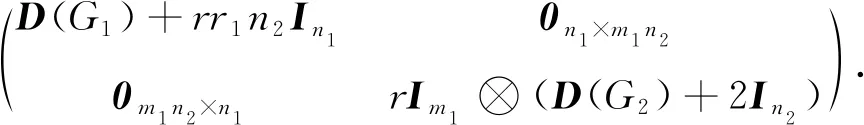


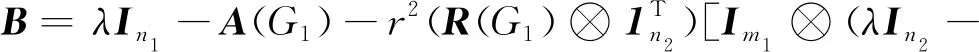
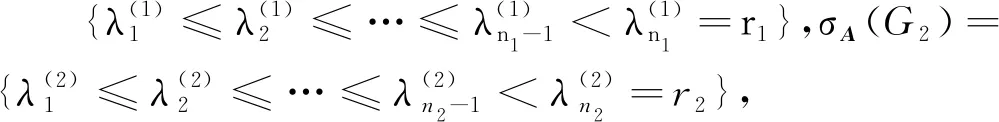
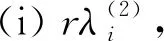


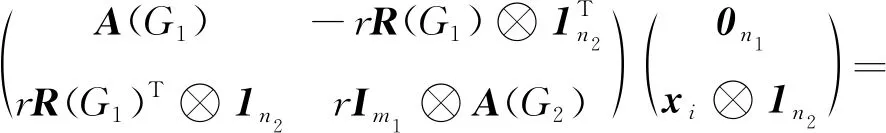

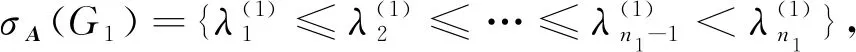


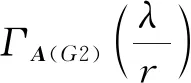

3 赋权边冠图G=G1◇G2的广义拉普拉斯谱
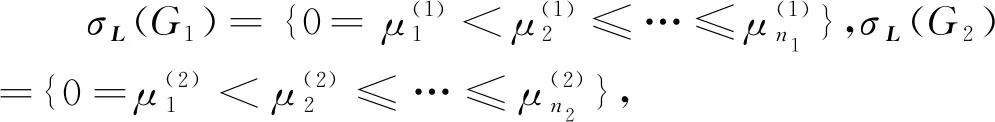
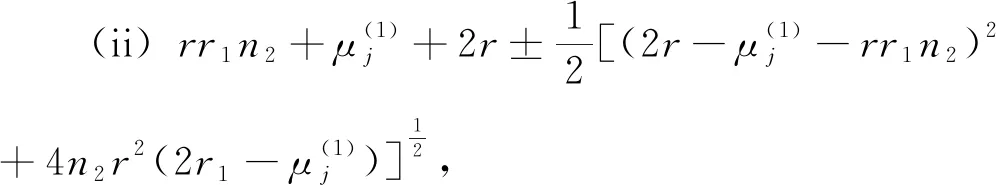
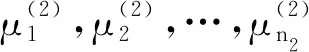


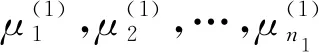
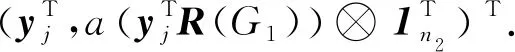
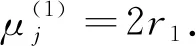
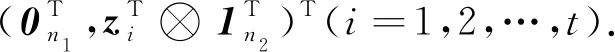

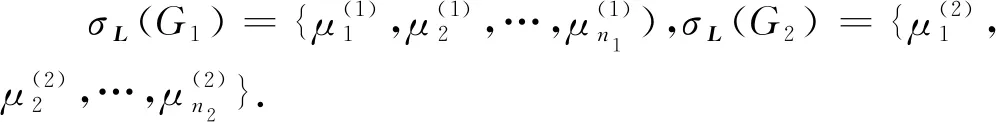
4 赋权边冠图G=G1◇G2的广义无符号拉普拉斯谱