果蔬类多孔介质干燥传质过程的分子动力学模拟

赵 哲，袁越锦，李林凤，徐英英，王泽群，熊奉奎

果蔬类多孔介质干燥传质过程的分子动力学模拟

赵 哲1，袁越锦2※，李林凤2，徐英英2，王泽群2，熊奉奎2

（1. 四川轻化工大学机械工程学院，宜宾 644000；2. 陕西科技大学机电工程学院，西安 710021）

果蔬类多孔介质内部水中溶解有大量的营养物质（溶质），在干燥过程中溶质的迁移与湿分的传递同时进行，其内部微孔内的干燥传质机理尚不明确。为了揭示果蔬类多孔介质干燥过程中内部溶液的迁移机理，确定果蔬微孔结构特性对干燥传质过程的影响规律，该研究采用分子动力学方法模拟研究了果蔬类多孔介质微孔道中的干燥传质过程，构建了光滑壁面溶液扩散过程模型与粗糙壁面溶液扩散过程模型。模拟过程采用SPC/E水分子模型，选取OPLS-AA全原子力场和正则系综，溶液势函数选用静电库伦相互作用与Lennard-Jones相互作用，中心水分子的初始速度由高斯分布给出，采用Velocity-Verlet算法，用SHAKE算法固定水分子，、方向施加周期性边界条件，方向上施加固定壁面边界条件。从分子水平模拟分析了果蔬类多孔介质内部溶液的扩散过程，并以马铃薯的热风干燥试验结果进行模型的验证。得出试验值与KCl溶液粗糙壁面模型的模拟值最为接近，其最大相对误差为17.39%；与纯水模型的模拟值相差最大，说明溶质的存在对水分扩散系数的影响不可忽略，且粗糙壁面模型更接近于真实孔道结构。从径向分布函数分布可以看出K+、Cl-对水分子的氢键结构有破坏作用。K+、Cl-均存在两层水化层，H2O分子以O原子靠近K+，以H原子靠近Cl-。溶质浓度、孔道直径、壁面粗糙度因子和相面积分数均对孔隙中的水分扩散系数有重要影响。随着孔道内KCl溶液质量分数的增大，其水分扩散系数逐渐减小。孔道直径变大、粗糙壁面粗糙度因子减小和粗糙壁面相面积分数增大，均会导致干燥过程中水分扩散系数增大。研究结果可为果蔬干燥品质及工艺优化分析提供理论依据。

果蔬；干燥；多孔介质；扩散系数；分子动力学

0 引 言

对于在受限孔道中溶液的传输扩散过程，国内外学者已经做了很多研究[10-13]。但纳米通道中的流量检测会遇到更基本的问题，例如可见光的最小空间分辨率约为300 nm[14]，示踪分子在可视化微通道流动方面的适用性也有限[15]。到目前为止，尚未明确多孔介质干燥过程中纳米孔中的传质机制[16]。微观世界中发生了什么，例如营养物质-水相互作用、氢键网络和离子吸附，仍然不清楚。因此，有必要从分子或原子水平进一步分析溶液的扩散过程。分子动力学模拟可以很好地区分离子和水的吸附和传输，它已被广泛用于离子传输过程中。KIM等[17]通过分子动力学模拟得出沿着流动方向沟槽内的水和离子扩散显著降低。SUN等[18]通过分子动力学模拟了胺分子在凝胶纳米通道中的行为，发现水分子的扩散系数降低是因为其与胺分子形成了更多的氢键。TANG等[19]使用分子动力学模拟研究了NaCl和CaCl2溶液通过1.5、3、5和10 nm伊利石孔道，利用均方位移和扩散系数表征了阳离子和水分子在各种纳米通道中的扩散特性。ZHOU等[20]进行了纳米孔中氯原子的迁移与吸附研究。HOU等[21]发现在纳米孔道传输过程中NaCl溶液表面会产生弯液面。王旭阳等[22]利用分子动力学方法研究了不同浓度氯化钠溶液的扩散过程。由此可见，采用分子动力学方法是研究微孔道中溶液扩散传质过程的有力手段。目前，该方法尚未应用于果蔬干燥过程中物料内部溶液的迁移研究。

本文以马铃薯中的无机盐（KCl）为例，利用分子动力学方法建立光滑壁面和粗糙壁面溶液扩散模型，分析其干燥过程中孔道内部溶液的扩散传递过程，对溶液浓度、孔道直径、孔道壁面粗糙因子和相面积分数等因素与干燥过程中溶液扩散系数的关系进行研究，以探究果蔬类多孔介质干燥过程中的传质规律。此外，从微观层面研究干燥传质过程将为干燥过程中营养物质的流失提供重要的理论支持。

1 模型建立

果蔬多孔介质的骨架主要是由纤维素、半纤维素和果胶质等组成。碳元素在其中占有很大的比例，且在干燥物料孔道内部起着支撑结构的重要作用。因此，选用碳原子作为构建壁面的基本构成原子，将碳原子按照面心立方晶体（face center cubic，FCC）结构来建立孔道固相壁面模型。在干燥过程中，壁面厚度不会影响孔道中溶液的扩散传递过程。新鲜马铃薯的含水率为76.2%[23]，其中各营养成分所占比例为淀粉16.5%、蛋白质2%、脂肪0.2%、膳食纤维0.7%、钾0.4%、钙0.06%等[24]。热风干燥马铃薯切片，热风温度为62 ℃，相对湿度为5%，风速为0.62 m/s，得到其平均孔径为4.5 nm，孔壁粗糙度为2，相面积分数为0.5[25]。

1.1 模型构建

借助Material Studio软件，构建了图1和图2所示的光滑壁面溶液扩散过程模型与粗糙壁面溶液扩散过程模型。

图1 孔道内光滑壁面溶液扩散过程模型

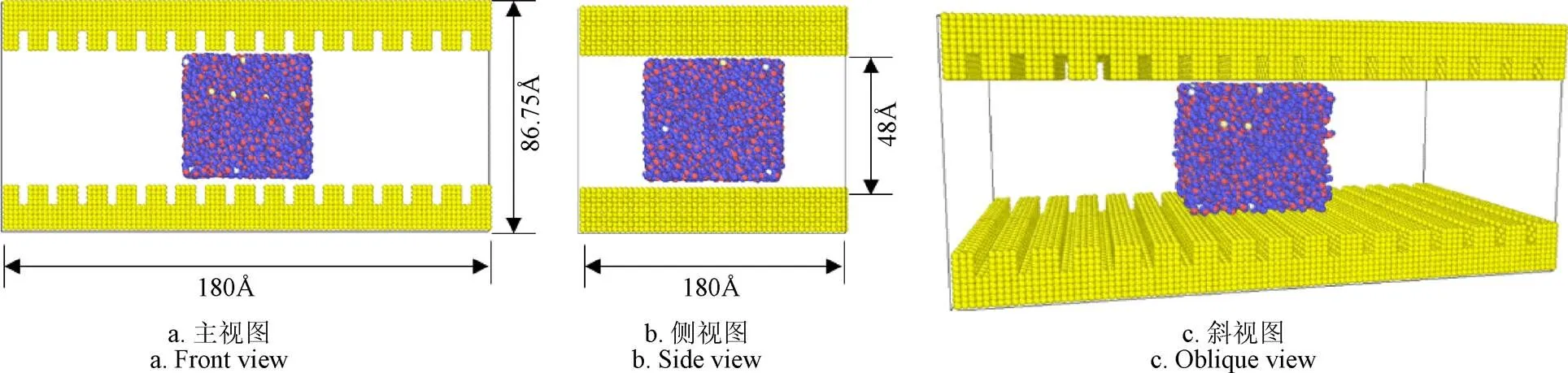
图2 孔道内粗糙壁面溶液扩散过程模型

图3所示为质量分数2%的KCl溶液模型，其中含有2 868个水分子，14个钾离子和氯离子。

注：红色代表氧原子（O）、紫色代表氢原子（H）、黄色代表钾离子（K+）、白色代表氯离子（Cl-），液滴的大小尺寸为45 Å×45 Å×45 Å。

采用SPC/E水分子模型，模型具体参数信息如表1所示。KCl的具体参数信息如表2所示。

根据实际情况，细胞壁具有不同的粗糙度，其主要由相面积分数和粗糙度因子两个参数来表示。如图4所示，其计算式如下[28]：

从表3可以看出，高温养护时，胶凝材料固铅试样各个龄期的浸出结果均低于地下水环境质量Ⅲ类标准0.05 mg·L-1的要求。水泥固铅试样各个龄期的浸出浓度要明显低于标准养护时的浓度。30 ℃养护下水泥试样28 d龄期的铅离子浸出浓度较3 d和7 d龄期降低的幅度更大，使得水泥试样28 d龄期的铅离子浸出浓度大幅降低，可见利用水泥固化稳定化铅离子更适合在30 ℃下进行[9]。

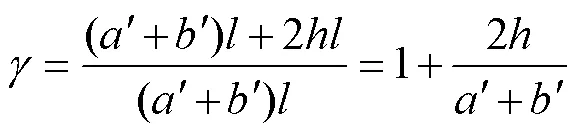
式中′为的栅栏宽度，nm；′为凹槽的宽度，nm；为栅栏的长度，nm；为凹槽的深度，nm。

1.2 势函数

分子动力学方法是从原子间相互作用势函数出发，基于牛顿第二定律来求解体系中各原子的运动轨迹，进而获取体系随时间的演化过程。因此，原子间相互作用势函数的可靠性直接决定所得原子运动轨迹的准确性，是分子动力学模拟的基础[29]。静电库伦相互作用与Lennard-Jones作用共同构成了溶液势函数，如下式所示[30-31]：

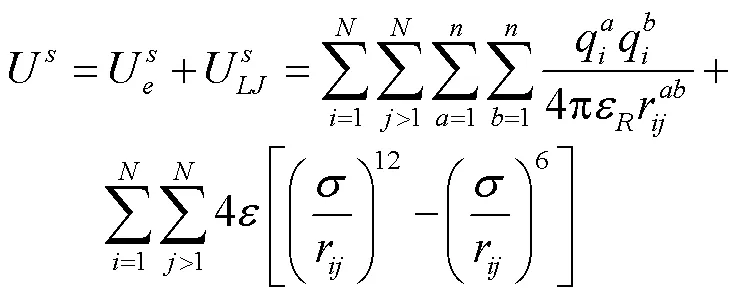
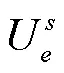
表1 SPC/E水分子模型参数表[26]

表2 氯化钾离子模型参数表[27]

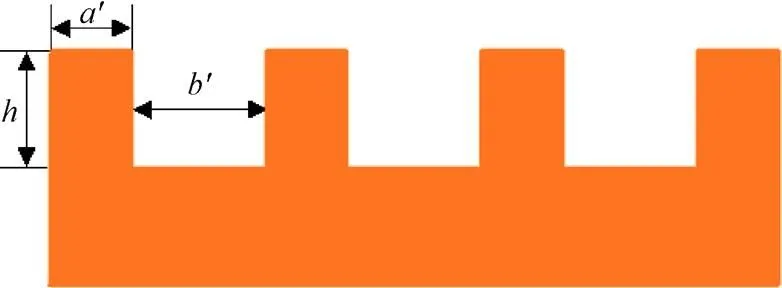
注：a′、b′、h为的栅栏的宽度、凹槽的宽度、凹槽的深度，mm。

1.3 扩散系数

用Einstein方程计算扩散系数，如下所示[32]：

式中D为扩散系数，m2/s；为被标记的粒子数；()为被标记的粒子在时刻的位置，m；(0)为被标记的粒子在0时刻的位置，m；为时间，s。

1.4 径向分布函数

径向分布函数（RDF）计算式如下[33]：

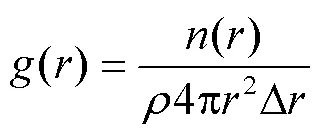
式中()表示距离中心参考粒子为处，宽度为Δ的球壳内某一粒子的平均数目，为系统中粒子的平均密度。值不断增大时，径向分布函数的数值无限接近于1。

2 模型求解

模拟过程选取OPLS-AA全原子力场和正则系综。中心水分子的初始速度由高斯分布给出，采用Velocity-Verlet算法更新原子的位置和速度，用SHAKE算法固定水分子。对模拟孔道的、方向施加周期性边界条件，方向上施加固定壁面边界条件[34-35]。在计算过程中，由于非键相互作用Lennard-Jones势和长程静电相互作用，都会随着粒子间距离增大而衰减的非常快，如果考虑更长距离的相互作用会耗费更多的计算资源。当非键相互作用Lennard-Jones势的截断半径为2.5时造成的相对误差很小，而长程静电相互作用的截断半径比之稍有增加。因此库仑相互作用力的截断半径设置为12 Å，粒子间相互作用力的截断半径设置为10 Å[36]。体系控温方法为速度标定法，模拟时间步长为1 fs，总模拟步数为700 000步，平衡过程为前500 000步，计算各类宏观性质为平衡后的200 000步。

3 结果与分析

3.1 孔道内的扩散过程

在温度为323 K的情况下，进行了纯水与KCl溶液在孔道平滑壁面中的扩散模拟，结果如图5所示。孔道直径设置为45 Å，粗糙因子设置为=1。图5a可以看到在模拟时间为100 ps时，已经出现了液滴边缘水分子吸收外界环境的能量，由液相状态脱离水分子之间的氢键作用力而变为气相。同时，可以看到液滴边缘由于受到孔道内部光滑壁面的吸附力以及水分子的内聚力，出现了靠近壁面的位置溶液铺展而孔道中心位置溶液收缩的现象。在孔道中形成了弯液面，使弯曲表面具有向外的附加压力（即毛细管力），从而导致了开尔文效应的产生[37]。随着模拟的进行，气相水分子的个数逐渐增加。图5b可以看到与纯水不同的是，KCl溶液液滴出现弯液面的时刻向后推迟了。这是因为K+和Cl-对水分子具有吸引力，水合作用导致孔道壁面对水分子的吸附力变弱。

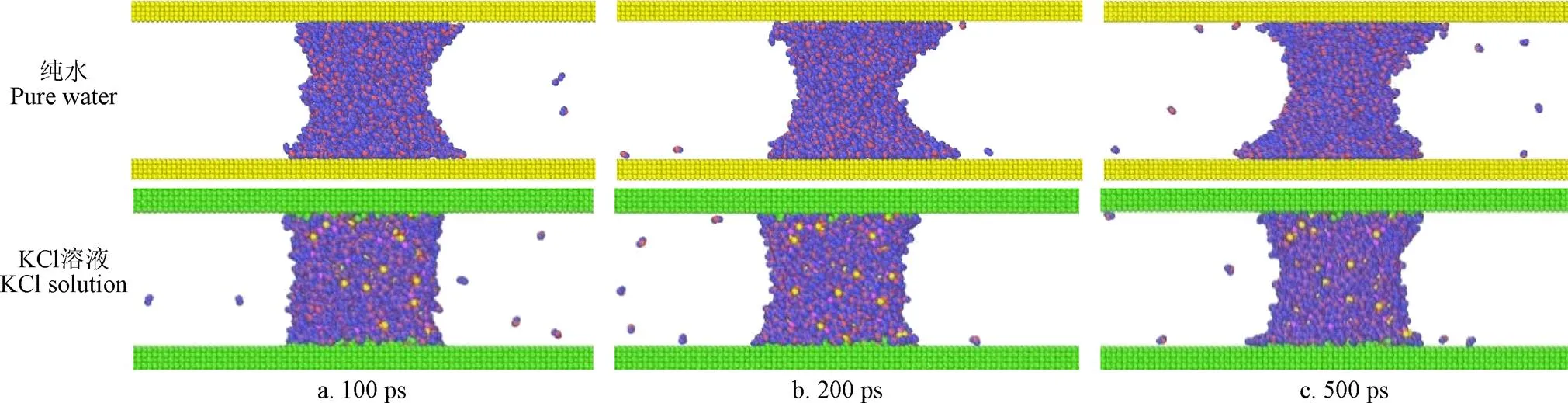
图5 不同时刻下纯水与KCl溶液在孔道中的扩散过程图

3.2 模型验证

干燥过程中水分的迁移在宏观尺度上比较慢，但在分子尺度可以在很短的时间内到达扩散过程的平衡态。当模拟过程进行到200 ps的时候均方位移曲线已经趋于稳定，且在前期的研究中对比发现，200、250和300 ps计算得出的扩散系数相差不大，出于计算量的考虑，选择200 ps进行扩散系数的计算。图6为3种模型在不同干燥温度下的均方位移曲线图，其中粗糙壁面的孔壁粗糙度为2，相面积分数为0.5。通过线性拟合可以得出每条曲线的斜率，进而通过Einstein方程即可得出其对应的水分扩散系数。图7为多孔介质干燥过程中，温度分别为313、323、333、343和353 K时纯水和质量分数为25%的KCl溶液的扩散系数模拟值与试验值的对比。随干燥温度的升高，孔道中的水分子扩散系数逐渐增大，这是由于外界干燥温度的升高，使得微孔道中的水分子运动变得剧烈，挣脱了水分子之间氢键的相互作用。马铃薯切片在不同热风温度下的水分扩散系数测量值由冯晞等得出[38]。从图7中可以看出，试验值与KCl溶液粗糙壁面模型的模拟值最为接近，最大相对误差为17.39%，其次为KCl溶液光滑壁面模型的模拟值，与纯水模型的模拟值相差最大。说明溶剂的存在对水分扩散系数的影响不可忽略，且粗糙壁面模型更接近于真实孔道结构。

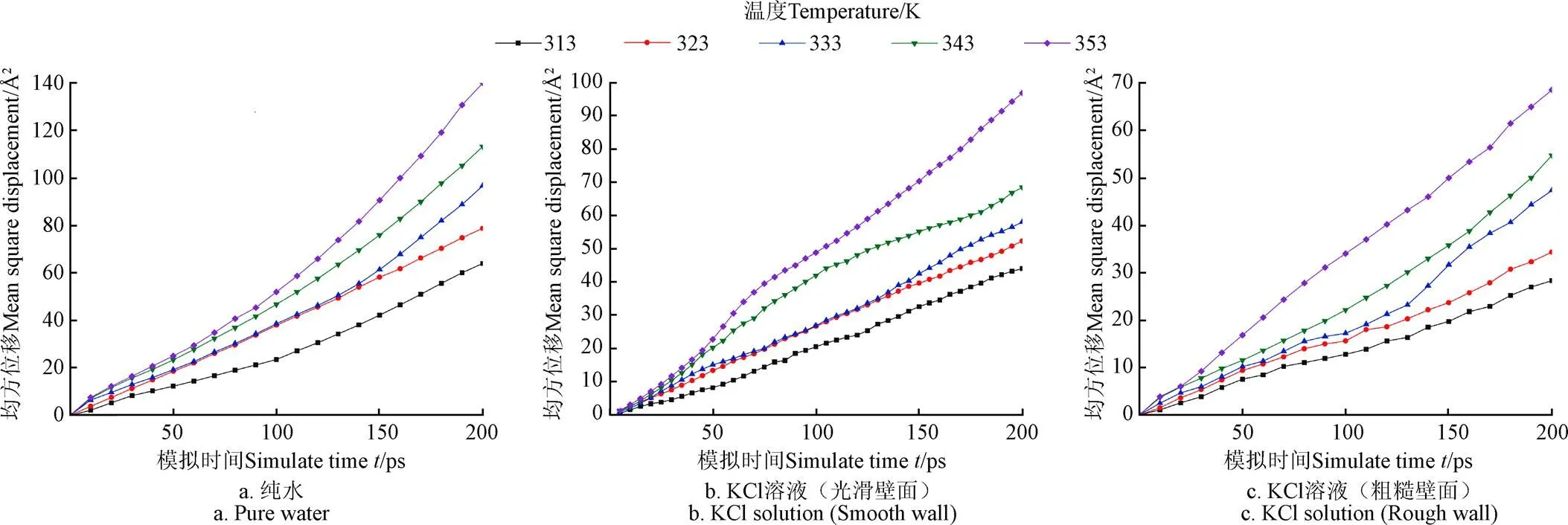
图6 不同干燥温度下三种模型的均方位移曲线图

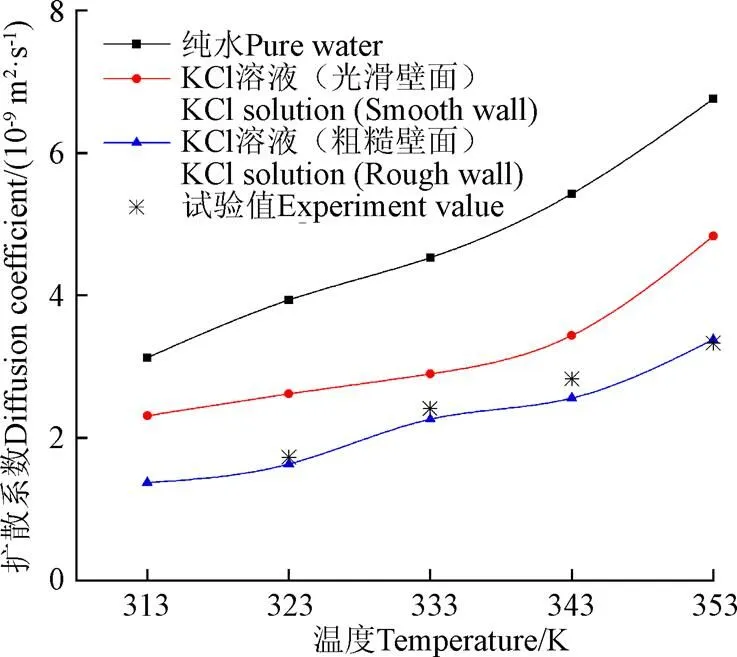
图7 不同干燥温度下三种模型与试验值的扩散系数对比

3.3 干燥过程中径向分布函数

径向分布函数是反映流体微观结构的物理量，可以体现液体中分子的聚集特性，以及中心粒子与其他粒子之间的相互作用强弱，在较远处趋向于1表示粒子与粒子之间的相互作用非常弱，已经接近理想气体。但是径向分布函数不具有方向性，无法反映不同扩散方向分子浓度的分布差异。在温度为323 K，孔道直径为45 Å，粗糙因子为1的情况下，得出孔道中不同质量分数KCl溶液的O-O、H-O和H-H径向分布函数。图8a和图8b为不同质量分数KCl溶液的O-O径向分布函数曲线。随着KCl溶液质量分数的增大，O-O之间第一峰的峰位基本保持不变，为0.258 nm；第一峰的峰值由质量分数1%溶液的7.915减小到25%溶液的6.703。随着溶液质量分数的增加，第一峰的峰谷逐渐抬升，第二峰的峰值逐渐降低，表明KCl溶液中水分子的四面体结构并未遭到破坏。图8c和图8d为不同质量分数的KCl溶液中H-O径向分布函数曲线。溶液中的H-O之间存在两个比较明显的峰。质量分数的变化对两个峰的峰位影响并不大，第一峰为尖峰，这是由于在H-O之间形成了氢键，使得H原子与O原子之间的分布比较规律，第二峰为宽峰，这是由于H原子与O原子之间的距离变大导致两种原子之间的静电相互作用减弱，原子间的分布发生变化。第一峰的峰值位于0.162 nm，第二峰的峰值位于0.306 nm。随着溶液质量分数的增加，第一峰的峰值由质量分数1%溶液的3.587减小到25%溶液的3.255，这说明KCl浓度的大小在一定程度上影响到了H2O分子在多组分溶液中的分布。图8e和图8f为不同质量分数KCl溶液的H-H径向分布函数曲线。溶液中的H-H之间前两个峰较为明显。质量分数的增大并没有对峰位产生影响，第一峰的峰值位于0.222 nm，第二峰的峰值位于0.366 nm。且都为宽峰，这是由于在KCl溶液中H2O分子之间是以O原子与H原子之间的相互作用为主，而H-H之间的相互作用受H-O之间的相互作用影响。

图8 孔道中不同质量分数KCl溶液的O-O、H-O、H-H径向分布函数

图9为不同质量分数KCl溶液中K+-O、K+-H径向分布函数曲线。通过对比可以得出，H2O分子以O原子靠近K+，这反映了K+离子与H2O分子间接触的选择性。从K+-O径向分布函数曲线可以看出在K+周围除了0.270 nm处存在第一水化层，在0.426 nm处存在第二水化层。第一峰的峰值较高且为尖峰，这源于K+周围的第一层水化作用较强，K+周围的H2O分子排列紧密。第二峰峰值较低且为宽峰，这源于K+与O原子的距离较远，两种粒子的相互作用较弱，H2O分子排列较松散。质量分数的增大并没有对峰位产生影响，随着KCl溶液质量分数升高，第一峰的峰值由1% KCl溶液的8.004降低到25% KCl溶液的4.939。从K+-H径向分布函数曲线可以看出随着溶液质量分数的增大，两峰的峰位并没有明显变化，第一峰的峰位在0.318 nm，第二峰的峰位在0.522 nm，第一峰的峰值由质量分数6% KCl溶液的4.371降低到25% KCl溶液的2.483。

图9 孔道中不同质量分数KCl溶液的K+-O、K+-H径向分布函数

图10为不同质量分数KCl溶液中Cl--O、Cl--H径向分布函数曲线。通过对比可以得出，H2O分子以H原子靠近Cl-，这是由Cl-离子与H2O分子中氢原子和氧原子间的静电作用决定的。从Cl--O径向分布函数曲线可以看出前两个峰较为明显，质量分数的增大并没有对峰位产生影响。第一峰的峰位在0.306 nm，峰值由质量分数1% KCl溶液的6.002降低到25% KCl溶液的4.040，第二峰随着KCl溶液质量分数的增大而逐渐消失。从Cl--H径向分布函数曲线可以看出溶液中的Cl--H之间前两个峰较为明显，在Cl-周围存在两层水化层，第一水化层在0.222 nm，第二水化层在0.354 nm。KCl质量分数的变化对两峰峰位影响可忽略。随着KCl溶液质量分数的增大，第一峰的峰值由1% KCl溶液的6.598降低到25% KCl溶液的4.277。第一峰的峰值较高且为尖峰，这是由于Cl-周围的第一层水化作用较强，使得Cl-周围的H2O分子排列紧密。

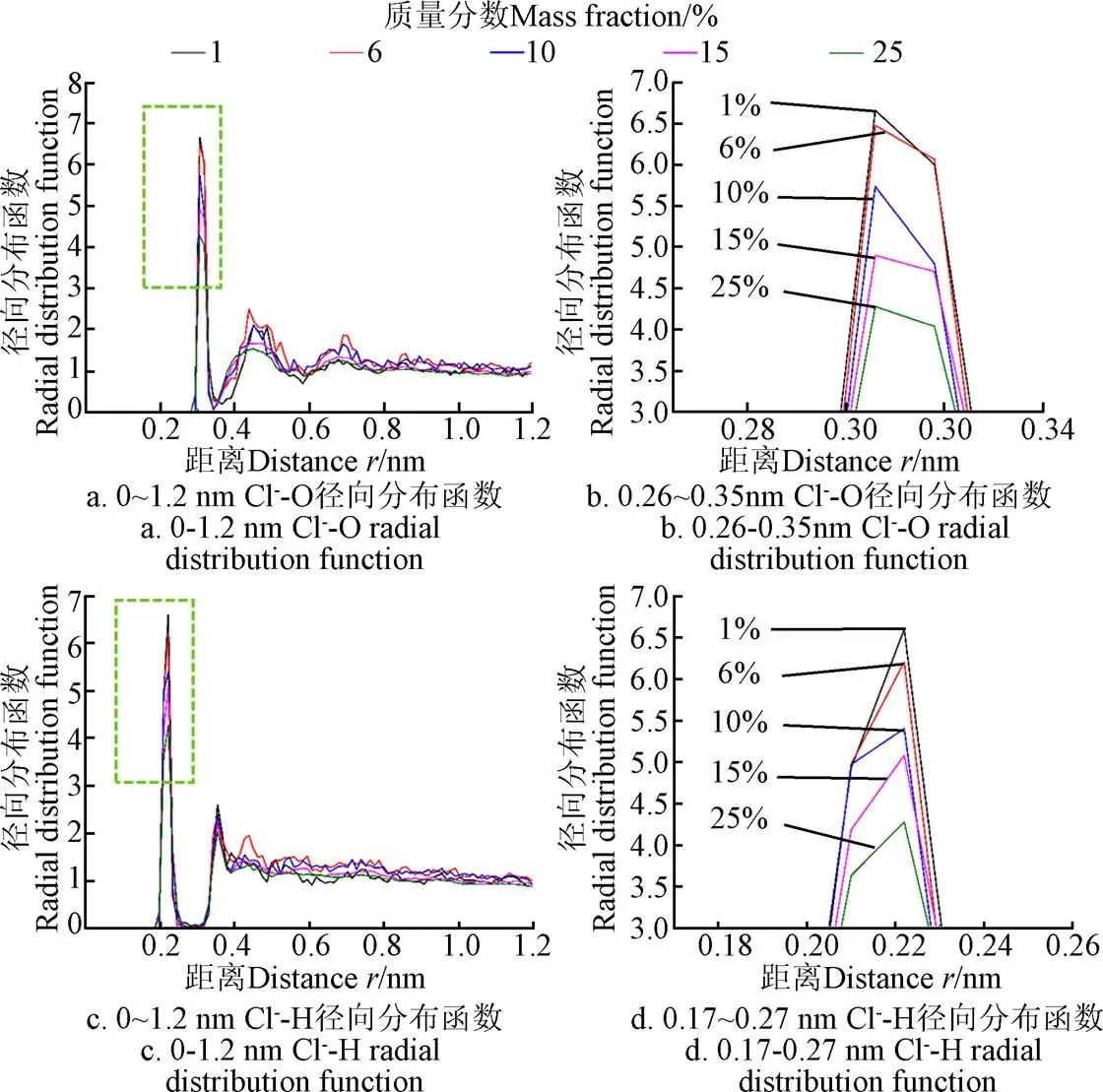
图10 孔道中不同质量分数KCl溶液的Cl--O、Cl--H径向分布函数

3.4 干燥过程中溶质浓度对溶液扩散系数的影响

不同质量分数KCl溶液的物理参数如表3所示。

表3 不同质量分数KCl溶液系统中的物理参数

温度为323 K时，在光滑壁面微孔道内不同质量分数的KCl溶液的均方位移和扩散系数变化曲线图如图11所示。可以看出，纯水的扩散系数最大，随着溶液质量分数的增大，其扩散系数逐渐减小。通过对比干燥过程中的径向分布函数曲线，可以看出随着KCl溶液质量分数的增大，其()的值在相应的减小，也就意味着不同原子、离子之间的分布更加集中，进一步验证了溶液质量分数的增大导致扩散系数减小。

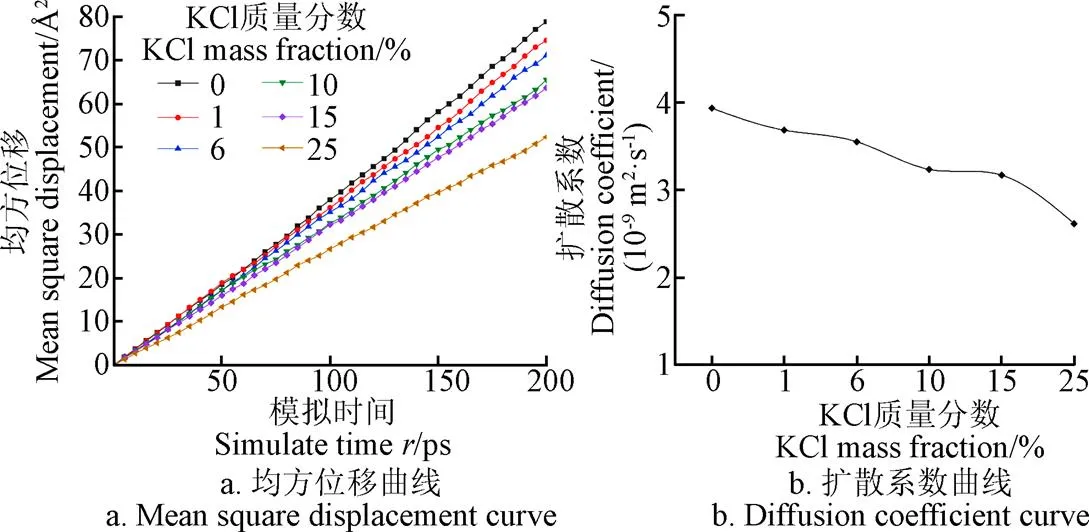
图11 不同质量分数的KCl溶液的均方位移和扩散系数曲线

3.5 干燥过程中孔径对溶液扩散系数的影响

模拟孔道直径分别为2.5、3.5、4.5、5.5、6.5 nm时，模拟时间为200 ps时的扩散过程。设置相面积分数=0.5，粗糙因子=2，KCl溶液质量分数为25%，获得KCl溶液在粗糙壁面中的扩散状态如图12所示。可以观察到，不同直径的孔道中KCl溶液液滴都会出现不同程度的弯液面。图13可以看出随着孔道直径由2.5 nm增大到6.5 nm，KCl溶液的扩散系数由2.351×10-10m2/s增大到6.028 1×10-9m2/s。这是由于孔道直径越大，壁面碳原子对溶液分子的作用越弱，溶液在孔道中扩散时受到的壁面阻力越小，导致溶液扩散系数不断增大。

图12 KCl溶液在不同孔道直径粗糙壁面孔道中的扩散现象

图13 KCl溶液在不同直径的粗糙壁面中的均方位移和扩散系数曲线

3.6 干燥过程中壁面粗糙度因子对溶液扩散系数的影响

通过前期的试验测得果蔬类物料的粗糙度因子几乎都在4.00以内，且根据模型的几何结构，设置壁面粗糙度因子分别为2.00、2.33、3.00、3.67、4.00，模拟时间为200 ps。设置相面积分数为=0.5，孔径为4.5 nm，KCl溶液质量分数为25%，得到液滴在的孔道中的扩散状态如图14所示。可以得出，当壁面存在凹槽时，由于势能的存在，部分KCl溶液就会被壁面原子吸附到凹槽里，这与YEN[39]观察到的现象一致。伴随着粗糙度因子不断增加，凹槽深度的值会不断加大，凹槽深度越来越深，凹槽中的KCl溶液越来越多，而停留在孔道中的KCl溶液减少。图15所示不同壁面粗糙因子的孔道中，KCl溶液的扩散系数随着粗糙因子的增大而减小。这是由于随着粗糙度因子的增加，粗糙壁面原子对溶液中的水分子、K+和Cl-的实际作用面积将变大，导致其吸附能力变强，另外，壁面上凹槽的存在也增大了KCl溶液在孔道内扩散的阻力。这与SOFOS等[40]的研究结论一致，其认为沟槽越深，扩散系数越小。

图14 KCl溶液在不同粗糙度因子（γ）粗糙壁面中扩散现象

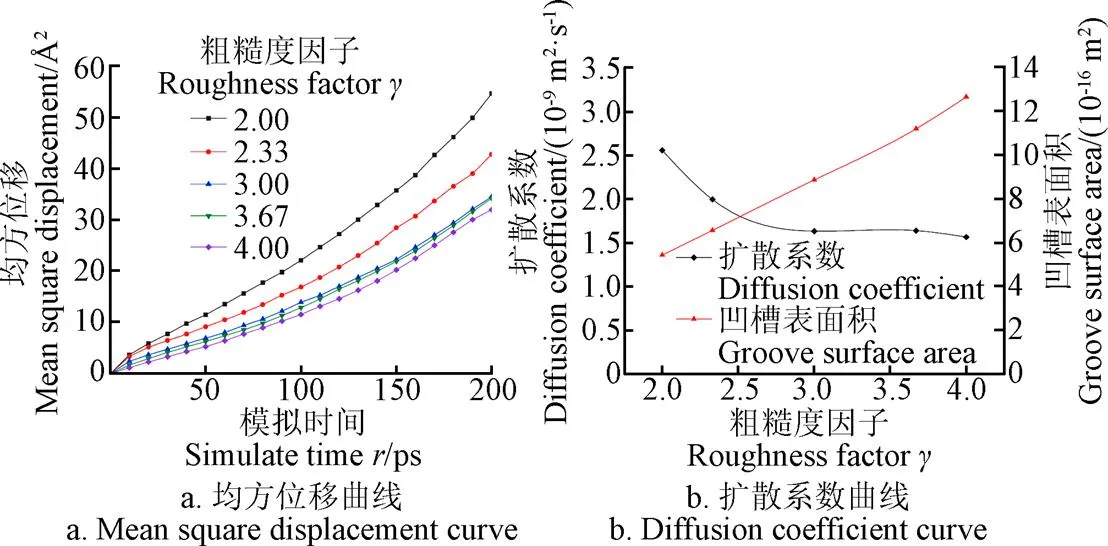
图15 KCl溶液在不同粗糙度因子壁面中的均方位移及扩散系数曲线

3.7 干燥过程中壁面相面积分数对溶液扩散系数的影响

模拟壁面相面积分数分别为0.2、0.3、0.4、0.5、0.6，模拟时间为200 ps时的扩散过程。设置粗糙因子=2，孔径为4.5 nm，KCl溶液质量分数为25%，得到液滴在的孔道中的扩散状态如图16所示。对比图16a和图16e可以看出，相面积分数增加，凹槽的有效作用面积减小，被吸附到凹槽中的KCl溶液减少。液滴的扩散系数随孔道壁面不同相面积分数的变化如图17所示。孔道中KCl溶液的扩散系数随相面积分数的增大而逐渐升高。这是由于相面积分数增大，凹槽越来越密集，凹槽的表面积越小，因此与壁面碳原子产生相互作用而被吸引到凹槽中的KCl溶液越来越少，导致壁面碳原子对KCl溶液的实际作用面积减小，液滴中所含的分子与离子在粗糙壁面中运动时的阻力减小，扩散系数增大。

图16 KCl溶液在不同相面积分数（φ）粗糙壁面中的扩散现象

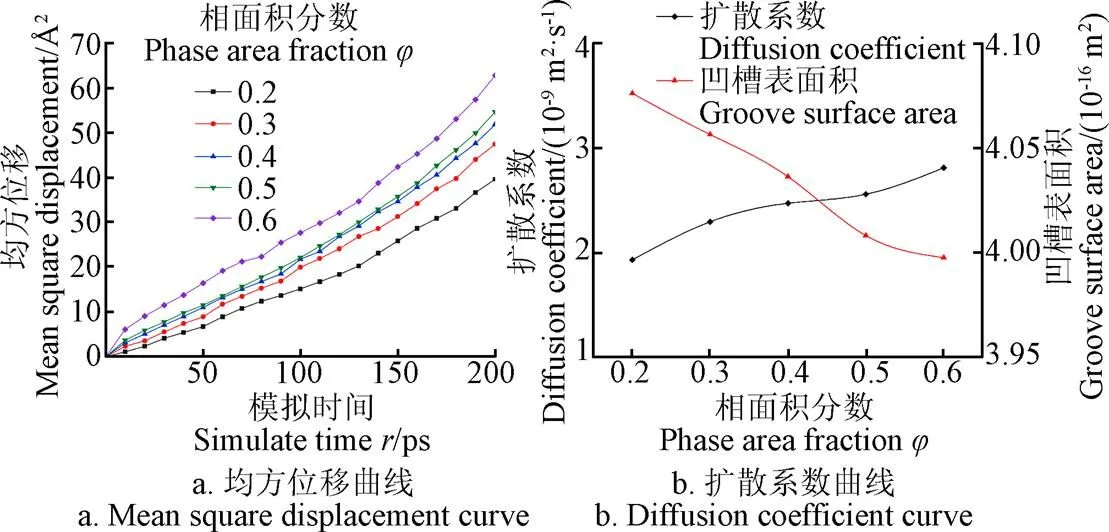
图17 KCl溶液在不同相面积分数壁面中的均方位移及扩散系数曲线

4 结 论

本文使用分子动力学方法模拟了果蔬类多孔介质微孔道中溶液的干燥过程，随着干燥的进行，孔道中形成了弯液面，且溶液出现弯液面的时刻比纯水靠后。通过对比可以看出，马铃薯切片热风干燥过程中水分的扩散系数试验值与KCl溶液粗糙壁面模型的模拟值最为接近，说明溶质的存在对水分扩散系数的影响不可忽略，且粗糙壁面模型更接近于真实孔道结构。

通过径向分布函数分析可以得出，K+、Cl-均存在两层水化层，H2O分子以O原子靠近K+，以H原子靠近Cl-。随着KCl溶液浓度的增大，其扩散系数逐渐减小。孔道直径越大，溶液在孔道中扩散时受到的壁面阻力越小，溶液扩散系数越大。随着壁面粗糙度因子的增加或者壁面相面积分数的减小，壁面对溶液分子的实际作用面积将变大，其吸附能力变强，导致溶液的扩散系数减小。在实践生产过程中为了提高生产效率，应该避免孔道的收缩及变形导致的孔道直径变小，粗糙度因子增加和相面积分数减小。

[1] 苑丽婧，何秀，林蓉，等. 超声预处理对猕猴桃水分状态及热风干燥特性的影响[J]. 农业工程学报，2021，37(13)：263-272.

YUAN Lijing, HE Xiu, LIN Rong, et al. Effects of ultrasound pretreatment on water state and hot-air drying characteristics of kiwifruit[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(13): 263-272. (in Chinese with English abstract)

[2] 代建武，杨升霖，王杰，等. 微波真空干燥对香蕉片干燥特性及品质的影响[J]. 农业机械学报，2020，51(S1)：493-500.

DAI Jianwu, YANG Shenglin, WANG Jie, et al. Effect of microwave vacuum drying conditions on drying characteristics and texture structure of banana chips[J]. Transactions of the Chinese Society for Agricultural Machinery, 2020, 51(S1): 493-500. (in Chinese with English abstract)

[3] 彭健，王蔚婕，唐道邦，等. 分段式远红外-热泵干燥对龙眼品质的影响[J]. 食品科学，2020，41(19)：118-123.

PENG Jian, WANG Weijie, TANG Daobang, et al. Effect of multi-stage far-infrared radiation-assisted heat pump drying on the quality characteristics of longan[J]. Food Science, 2020, 41(19): 118-123. (in Chinese with English abstract)

[4] 王瑞芳，王竟成，赵东海，等. 香蕉低压过热蒸汽-真空组合干燥研究[J]. 农业机械学报，2022，53(3)：392-399.

WANG Ruifang, WANG Jingcheng, ZHAO Donghai, et al. Drying of banana using combined low-pressure superheated steam and vacuum drying[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022, 53(3): 392-399. (in Chinese with English abstract)

[5] 王凤昭，吕健，毕金峰，等. 去皮方式对黄桃渗透脱水组合干燥特性及理化品质的影响[J]. 中国食品学报，2021，21(9)：121-129.

WANG Fengzhao, LV Jian, BI Jinfeng, et al. Effect of peeling methods on drying characteristics and physico-chemical properties of yellow peach prepared by combined osmotic dehydration and drying[J]. Journal of Chinese Institute of Food Science and Technology, 2021, 21(9): 121-129. (in Chinese with English abstract)

[6] 牛玉宝，姚雪东，肖红伟，等. 射频辅助热风干燥对红枣脆片质构特性和微观结构的影响[J]. 农业工程学报，2022，38(2)：296-306.

NIU Yubao, YAO Xuedong, XIAO Hongwei, et al. Effects of radio frequency assisted hot air drying on the texture and microstructure of jujube slices[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(2): 296-306. (in Chinese with English abstract)

[7] 姜大龙，王文杰，王善钰，等. 红外联合热风干燥白萝卜片的耦合建模与热质传递分析[J]. 农业工程学报，2022，38(1)：314-323.

JIANG Dalong, WANG Wenjie, WANG Shanyu, et al. Coupled modeling and heat and mass transfer analysis of white radish slices dried by infrared radiation combined hot air drying[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(1): 314-323. (in Chinese with English abstract)

[8] 徐英英，文怀兴，谭礼斌，等. 苹果切片干燥收缩变形的孔道网络模拟及试验[J]. 农业工程学报，2021，37(12)：289-298.

XU Yingying, WEN Huaixing, TAN Libin, et al. Pore network simulation and experiments of drying shrinkage-deformation for apple slices[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(12): 289-298. (in Chinese with English abstract)

[9] 王吉强，邓利珍，裴昱鹏，等. 成熟度对冬枣真空脉动干燥动力学及产品品质的影响[J]. 农业工程学报，2021，37(23)：273-279.

WANG Jiqiang, DENG Lizhen, PEI Yupeng, et al. Effects of maturity on pulsed vacuum drying kinetics and product quality of winter jujube[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(23): 273-279. (in Chinese with English abstract)

[10] YANG M, YANG X H, WANG Q, et al. Anomalous effects of water flow through charged nanochannel membranes[J]. Rsc Advances, 2014, 4(51): 26729-26737.

[11] QIAN S Z, DAS B, LUO X B. Diffusion osmotic flows in slit nanochannels[J]. Journal of Colloid and Interface Science, 2007, 315(2): 721-730.

[12] GREEN Y, ABU R R, ESHEL R. Electrical resistance of nanochannel-microchannel systems: An exact solution[J]. Physical Review Applied, 2020, 14(1): 014075.

[13] MA X, LI C, MARTINSON A B, et al. Water-assisted proton transport in confined nanochannels[J]. The Journal of Physical Chemistry C, 2020, 124(29): 16186-16201.

[14] SINTON D. Microscale flow visualization[J]. Microfluidics and Nanofluidics, 2004, 1(1): 2-21.

[15] KARNIK R, CASTELINO K, DUAN C H, et al. Diffusion-limited patterning of molecules in nanofluidic channels[J]. Nano Letters, 2006, 6(8): 1735-1740.

[16] SEGURA L A, OYARZUN C A. Experimental evidence of mass transfer mechanisms during freeze-drying in a capillary porous medium[J]. International Journal of Refrigeration-revue Internationale Du Froid, 2013, 35(8): 2102-2109.

[17] KIM D, DARVE E. Molecular dynamics simulation of electro-osmotic flows in rough wall nanochannels[J]. Physical Review E, 2006, 73(5): 051203.

[18] SUN D W, YAN J H, MA X Y, et al. On the characterization of amine molecules behaviors in the nanochannels forming in calcium silicate hydrate gel[J]. Applied Surface Science, 2021, 560: 149994.

[19] TANG L B, LI X, FENG H T, et al. Infiltration of salt solutions through illite particles: Effect of nanochannel size and cation type[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2022, 641: 128581.

[20] ZHOU Y, HOU D, JIANG J, et al. Experimental and molecular dynamics studies on the transport and adsorption of chloride ions in the nano-pores of calcium silicate phase: The influence of calcium to silicate ratios[J]. Mesoporous Materials, 2018, 255: 23-35.

[21] HOU D, LI T, WANG P. Molecular dynamics study on the structure and dynamics of NaCl solution transport in the nanometer channel of CASH gel[J]. ACS Sustainable Chemistry & Engineering, 2018, 6(7): 9498-9509.

[22] 王旭阳，陈帅，李非，等. 氯化钠水溶液结构的研究[J]. 原子与分子物理学报，2020，37(5)：768-776.

WANG Xuyang, CHEN Shuai, LI Fei, et al. Study on the structure of sodium chloride aqueous solution[J]. Journal of Atomic and Molecular Physics, 2020, 37(5): 768-776. (in Chinese with English abstract)

[23] 尹慧敏，聂宇燕，沈瑾，等. 基于Weibull分布函数的马铃薯丁薄层热风干燥特性[J]. 农业工程学报，2016，32(17)：252-258.

YIN Huimin, NIE Yuyan, SHEN Jin, et al. Drying characteristics of diced potato with thin-layer by hot-wind based on Weibull distribution function[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(17): 252-258. (in Chinese with English abstract)

[24] 赖灯妮，彭佩，李涛，等. 烹饪方式对马铃薯营养成分和生物活性物质影响的研究进展[J]. 食品科学，2017，38(21)：294-301.

LAI Dengni, PENG Pei, LI Tao, et al. A review of the effects of cooking methods on nutritional components and bioactives in potato[J]. Food Science, 2017, 38(21): 294-301. (in Chinese with English abstract)

[25] XIAO Z F, YANG D Y, YUAN Y J, et al. Fractal pore network simulation on the drying of porous media[J]. Drying Technology, 2008, 26(6): 651-665.

[26] FANG Z, TANG S, WANG Z, et al. General synthesis of large inorganic nanosheets via 2D confined assembly of nanoparticles[J]. ACS Central Science, 2022, 8(5): 627-635.

[27] WANG L, MORITA A, NORTH N M, et al. Identification of ion pairs in aqueous NaCl and KCl solutions in combination with Raman spectroscopy, molecular dynamics, and quantum chemical calculations[J]. The Journal of Physical Chemistry B, 2023, 127(7): 1618-1627.

[28] ZHAO J, WANG B H, PAN Y Q, et al. Molecular dynamics simulation on wetting behaviors of n-octane and water droplets on polytetrafluoroethylene surfaces[J]. Chemical Physics Letters, 2021, 785: 139161.

[29] 许竞翔，冯建方，孙强，等. 海洋大气下几种常用金属腐蚀机理的分子动力学模拟综述[J]. 材料保护，2022，55(8)：140-149.

XU Jingxiang, FENG Jianfang, SUN Qiang, et al. A review of molecular dynamics simulation of corrosion mechanism of several commonly used metals in marine atmosphere[J]. Materials Protection, 2022, 55(8): 140-149. (in Chinese with English abstract)

[30] OWHAL A, GAUTAM D, BELGAMWAR S U, et al. Atomistic approach to analyse transportation of water nanodroplet through a vibrating nanochannel: scope in bio-NEMS applications[J]. Molecular Simulation, 2022, 48(9): 737-744.

[31] LE B G, JOLY L. Molecular modeling of aqueous electrolytes at interfaces: Effects of long-range dispersion forces and of ionic charge rescaling[J]. Journal of Chemical Physics,2020,152: 241102.

[32] CHEN G B, LIU Z W. Effect of modification on the fluid diffusion coefficient in silica nanochannels[J]. Molecules, 2021, 26(13): 4030.

[33] STEINCZINGER Z, JAVARI P, PUSZTAI L. Comparison of interatomic potentials of water via structure factors reconstructed from simulated partial radial distribution functions: A reverse Monte Carlo based approach[J]. Physica Scripta, 2017, 92(1): 014001.

[34] YU J P, WANG H. A molecular dynamics investigation on evaporation of thin liquid films[J]. International Journal of Heat and Mass Transfer, 2012, 55(4): 1218-1225.

[35] MAO Y J, ZHANG Y W. Molecular dynamics simulation on rapid boiling of water on a hot copper plate[J]. Applied Thermal Engineering, 2014, 62(2): 607-612.

[36] CHI C, AN M, QI X, et al. Selectively tuning ionic thermopower in all-solid-state flexible polymer composites for thermal sensing[J]. Nature Communications, 2022, 13(1): 221.

[37] MAALAL O, PRAT M, LASSEUX D. Pore network model of drying with Kelvin effect[J]. Physics of Fluids, 2021, 33(2): 027103.

[38] 冯晞，胡巧群，诸爱士. 马铃薯片热风对流干燥模型与特性[J]. 粮食与油脂，2018，31(7)：52-55.

FENG Xi, HU Qiaoqun, ZHU Aishi. Model and character of hot air convection drying of potato slice[J]. Cereals & Oils, 2018, 31(7): 52-55. (in Chinese with English abstract)

[39] YEN T H. Investigating the effects of wettability and gaseous nanobubbles on roughened wall-fluid interface using molecular dynamics simulation[J]. Molecular Simulation, 2017, 43(1): 1-12.

[40] SOFOS F, KARAKASIDIS T E, LIAKOPOULOS A. How wall properties control diffusion in grooved nanochannels: A molecular dynamics study[J]. Heat and Mass Transfer, 2013, 49(8): 1081-1088.

Molecular dynamics simulation of the mass transfer process for the drying of fruit and vegetable porous media

ZHAO Zhe1, YUAN Yuejin2※, LI Linfeng2, XU Yingying2, WANG Zequn2, XIONG Fengkui2

(1.,,644000,; 2.,,710021,)

A large number of nutrients (solutes) can be dissolved in the water inside the porous medium of fruits and vegetables. The migration of solutes can occur simultaneously with the transfer of wet content during drying. It is still lacking in the mass-transfer mechanism of drying in the internal micropores of fruit and vegetable porous media so far. It is a high demand to determine the influence of microporous structure characteristics of fruits and vegetables on the mass transfer process during drying. In this study, a systematic simulation was carried out for the mass transfer in the microporous media of fruits and vegetables during drying using molecular dynamics. The diffusion process model of smooth wall solution and the diffusion process model of rough wall solution were constructed after simulation. The SPC/E water molecular model was also selected under the OPLS-AA all-atomic force field and the regular ensemble. The solution potential function was established with the electrostatic Coulomb and Lennard-Jones interaction. Among them, the initial velocity of the central water molecule was given by the Gaussian distribution. The Velocity-Verlet algorithm was then used to update the position and velocity of atoms. The water molecules were fixed with the SHAKE algorithm. Periodic boundary conditions were applied in theanddirections of the simulated aperture, whereas, the fixed wall boundary conditions were applied in thedirection. The diffusion process of the internal solution was simulated in the porous media of fruits and vegetables from the molecular level. The improved model was verified using the hot-air drying experiment of potatoes. The experimental value was the closest to the simulated using the KCl solution rough wall model, where the maximum relative error was 17.39%. There was the largest difference between the experimental and the simulated value of the pure water model. Therefore, the rough wall model was much closer to the real pore wall structure, without considering the influence of the presence of solute on the water diffusion coefficient. The radial distribution function demonstrated that K+and Cl-posed damaging effects on the hydrogen bond structure of water molecules, while both K+and Cl-shared two hydration layers. The H2O molecule was close to K+with an O atom, and Cl-with an H atom. The important influences were obtained on the water diffusion coefficient in the pores, including the solute concentration, pore diameter, wall roughness factor, and phase area fraction. The diffusion process of KCl solutions with different mass fractions showed that the larger the solution mass fraction was, the smaller the water diffusion coefficient was. The optimal combination was achieved in the diffusion coefficient of the water during drying. Specifically, there was an increase in the pore diameter, drying temperature, and the area fraction of the rough wall, whereas, a decrease was observed in the roughness factor of the rough wall. The finding can also provide a theoretical basis to analyze the drying quality and process optimization of fruits and vegetables.

fruit and vegetable; drying; porous media; diffusion coefficient; molecular dynamics

2022-07-27

2023-03-10

国家自然科学基金项目（51876109），陕西省重点研发计划项目（2020KWZ-015）

赵哲，讲师，研究方向为干燥技术及机理。Email：122524889@qq.com

袁越锦，教授，研究方向为热能与干燥技术。Email：yyjyuan1@163.com

10.11975/j.issn.1002-6819.202207259

TS255.3; TQ021.4

A

1002-6819(2023)-07-0285-10

赵哲，袁越锦，李林凤，等. 果蔬类多孔介质干燥传质过程的分子动力学模拟[J]. 农业工程学报，2023，39(7)：285-294. doi：10.11975/j.issn.1002-6819.202207259 http://www.tcsae.org

ZHAO Zhe, YUAN Yuejin, LI Linfeng, et al. Molecular dynamics simulation of the mass transfer process for the drying of fruit and vegetable porous media[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2023, 39(7): 285-294. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.202207259 http://www.tcsae.org