基于PC-RELM的养殖水体溶解氧数据流预测模型

施 珮，匡 亮，王 泉，袁永明

基于PC-RELM的养殖水体溶解氧数据流预测模型

施 珮1,2，匡 亮3，王 泉1,2，袁永明4

（1. 无锡学院，无锡 214105；2. 江苏省物联网设备超融合与安全工程研究中心，无锡 214105；3. 江苏信息职业技术学院物联网工程学院，无锡 214153；4.中国水产科学研究院淡水渔业研究中心，无锡 214081）

养殖水体中溶解氧浓度一直是最重要的水质参数之一。为了精准地对水体溶解氧进行调控，提高养殖生产效率，降低养殖风险，该研究考虑外部天气条件对溶解氧的影响以及溶解氧自身的昼夜变化特征，提出一种基于正则化极限学习机（principal component analysis and clustering method optimized regularized extreme learning machine，PC-RELM）的养殖水体溶解氧数据流预测模型。首先，采用主成分分析法判断影响溶解氧浓度的强重要性因子，降低预测模型的数据维度；其次，利用熵权法计算各时刻点的天气环境指数，并利用快速动态时间规整算法（fast dynamic time warping，FastDTW）完成时间序列数据流在不同天气环境下的相似度度量；然后使用-means算法对时间序列的相似度进行聚类分簇，并基于分簇结果完成正则化极限学习机预测模型的构建，实现溶解氧浓度的估算。最后将PC-RELM模型应用到无锡南泉试验基地养殖池塘的溶解氧预测调控过程中。试验结果表明：PC-RELM的预测均方根误差值（root mean square error， RMSE）为0.961 9，与PLS-ELM（partial least squares optimized ELM）、最小二乘支持向量机（least square support vector machine，LSSVM）以及BP神经网络模型进行对比，其RMSE值分别降低了41.54%、54.58%和67.16%。该预测模型可以有效地捕捉不同天气条件下溶解氧的变化特点，具有较高的预测精度和效率。

溶解氧；养殖；水质；聚类；快速动态时间规整算法；正则化极限学习机

0 引 言

溶解氧浓度作为大规模高密度淡水养殖中的重要水体指标，当其浓度过高时易引起鱼类发生气泡病，浓度过低则会使得鱼类生长缓慢，长时间的浮头更会引发鱼类死亡等问题[1]。溶解氧（dissolved oxygen，DO）浓度的变化研究具有明显的非线性和复杂性[2]，水体环境和天气条件均对水体DO浓度的变化有直接和间接的影响。养殖水体的精准监测和预测，能够帮助养殖从业者及时了解养殖环境，实现溶解氧浓度的精准调控，有效降低养殖风险。

当前水质数据流的预测研究主要分为单因子预测和多因子预测[3]。在单因素预测方面，Ahmad等[4]利用随机模型对印度恒河10 a间采集的溶解氧数据流进行预测，并构建预测模型分别实现温度、氯化物、pH值等水质参数数据流的预测。在多因素预测方面，Palani等[5]从复杂环境因子角度构建人工神经网络对水体盐度、温度、DO、叶绿素等指标进行定量特征预测。Najah等[6]利用多层感知器神经网络、集成神经网络和支持向量机来预测DO、生化需氧量和化学需氧量等水质参数。Ahmed等[7]利用回归森林和机器学习技术开发了基于多因素数据驱动的DO预测模型。但是该类预测模型构建的预测指标体系仅限于水体参数间的关联关系，忽略了天气条件对水体参数的影响。因此，一些研究从多个方面选择不同的关联因素进行预测，并利用各种优化算法不断提高预测性能。张阳等[8]利用水质数据的空间相关性构建神经网络模型实现对河流水质参数溶解氧和氨氮进行实时预测和分析。LIU等[9]利用水质指标和太阳辐射、气温、风速等气象因子，采用最优改进柯西粒子群优化算法，建立了基于小波分析和最小二乘支持向量回归（least square support regression，LSSVR）的混合溶解氧预测模型。然而溶解氧参数存在一定的复杂性，这些预测模型都存在运行时间长、泛化性能低、通用性差的缺点。

近年来，极限学习机（extreme learning machine， ELM）作为一种高效的前馈神经网络在各领域内被广泛应用[10]。同时，各种智能算法也被用来优化ELM模型，以提高其性能[11-17]。CAO等[18]利用灰色关联分析、集合经验模态分解、样本熵和RELM提出了一种基于多因素、多尺度的溶解氧预测模型。宦娟等[19]针对溶解氧原始序列分解后高频、中频、低频分量呈现的特点，提出一种基于集合经验模态分解、游程检测法重构、单项预测算法和BP神经网络非线性叠加的组合预测模型，对池塘溶解氧进行预测。但是，在实际应用过程中，该模型还存在参数复杂、计算效率不够高等问题。

因此，本文提出了一种基于相似时间段聚类机制的正则化极限学习机模型（PC-RELM）对养殖池塘水体溶解氧浓度进行预测。该模型通过定义天气环境指数将昼夜时间序列的相似度进行有效度量，使得基于相似时间段的-means聚类过程可以捕捉水体溶解氧变化的潜在规律，改进的极限学习机模型在训练过程中可以快速学习样本数据的相似变化趋势，得到溶解氧和各天气指标、水质指标之间的映射关系，从而对养殖水体的溶解氧浓度进行高效准确地预测。

1 材料与方法

1.1 试验区域与数据源

本文中所有数据采集自江苏省无锡市南泉水产养殖试验基地（北纬31°43，东经120°29），该基地紧邻太湖，养殖池塘较多。本次养殖试验是在4个具有循环水养殖系统的测试池塘进行，池塘配备物联网监测系统、多种水下传感器、增氧设备、尾水处理设备和自动气象站。4个试验池塘面积相近，约1 800 m2（30 m×60 m），池塘的深度为1.5 m。池塘养殖品种为加州鲈鱼，养殖投放密度为2.8尾/m2。所有数据均通过物联网监测系统和自动气象站进行采集，其结构如图1所示。

图1 养殖监测系统结构

由如图1可知，系统部署的多种水下传感器包括溶解氧传感器、pH传感器和温度传感器。岸边安装的自动气象站可同时采集多种天气环境数据，包括气温、湿度、气压、二氧化碳、光照强度、光合有效辐射、辐射照度、风速和风向等。传感器数据通过GPRS从感知设备传输至服务器，用户可通过手机移动端或计算机PC端接入服务器，实时观察水质数据和气象数据。试验设计参考文献[1-2]，采用扩大试验周期和数据集，选择加州鲈鱼养殖周期内2019年7月9日至9月9日期间共62 d的水体参数数据流信息和天气环境数据约8 967个数据集，样本采样频率为10 min/次。试验选取前7 077个(约80%)的数据样本作为训练集，其余1 890个数据样本作为测试集。

1.2 时间序列相似度分析

在养殖水体中，DO浓度一直受水体环境和天气条件的影响，具有明显的昼夜变化特征。同时，在相似的天气条件下，DO也会呈现一定的变化规律。因此，依据监测数据流的昼夜变化特征，需要对数据流进行时间段划分，并度量时间序列数据流之间的相似度。由于时间序列长度不一定相等，需要采用适宜的算法实现相似度度量。动态时间规整算法（dynamic time warping，DTW）是一种适用于长度不等的时间序列距离度量方法，较广泛应用于语音序列的识别[20]。

在DTW算法中，假设2个时间序列{1,2, …,R}和{1,2,…,V}，它们的序列长度分别为和，由序列和构建一个×的距离矩阵×e，矩阵中每个元素（,）对应于一个基距离= (−)2。

DTW距离是将序列和上每个点之间建立对齐匹配关系，每种匹配关系可以用一条弯曲距离进行表示，DTW距离即为点对基距离之和的最小值。{w}={1,2,…,w}（=1～）为DTW算法获得的弯曲路径距离，w为弯曲距离的第个元素，时间序列与之间的DTW距离值则表示为

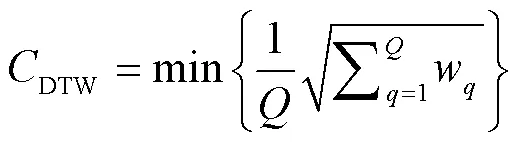
在使用DTW算法计算弯曲路径时，若时间序列长度较长，则会出现运行效率不高的问题。FastDTW算法不同于传统DTW算法，它通过限制和数据抽象2种方法完成DTW距离值的快速计算[21]。该算法能在和序列之间找到近似最优的弯曲路径，降低运算时间复杂度。实现过程包括粗粒度化、投影、细粒度化等步骤。

1）粗粒度化。即通过数据抽象的形式对原序列进行抽象，用一半的时间序列采样点表征原时间序列，使得缩减后的时间序列上每个采样点的值为原序列相邻两点的均值，从而通过迭代的方式执行粒度矩阵的抽象过程。

2）投影。在较粗粒度距离矩阵上计算DTW值，从而找到弯曲路径。

3）细粒度化。通过弯曲路径经过的方格完成从粗粒度矩阵到较细力度矩阵的对应细化过程。

通过对投影的弯曲路径方格进行搜索可以有效地减少算法的运行时间和时间复杂度，这是FastDTW算法的核心理念[22]。在最优弯曲路径搜索过程中，为了避免最优路径可能不在投影弯曲路径中的问题，FastDTW额外增加参数，使得投影弯曲路径方格的搜索可以扩大个方格。故当越大时，弯曲路径越精准；越小时，弯曲路径越粗略。

1.3 相似度聚类方法

聚类作为一种典型的无监督学习方法，可以有效地将样本分成若干类[23]。当样本属于未标记数据集时，聚类算法无需样本集训练即可发现样本的内在规律。天气环境时间序列之间的相似度可以有效的体现采样时刻点之间的关联性。当相似度值越低时，表明这些时间序列间的差异越大，且对应的天气环境实际状态差异性较大。反之，则差异性越小。

-means作为目前使用最广泛的聚类算法之一，该算法原理是从大小为的样本集中选定个样本点作为初始聚类中心，依据当前样本到这个簇类中心的距离长度，将样本分配到距离值最近的簇中，不断迭代，当簇类中心点变化很小，或达到指定迭代次数后终止迭代。在-means聚类算法中。其基本步骤如下：

1）在给定的个样本中随机选择个对象作为簇类的初始中心；

2）对每个样本点到最近的簇类中心的距离进行测算；

3）依据步骤2）计算的距离确定各样本在簇类中的归属情况，若距离值大于设定的阈值则生成新簇。依据式（3）计算号新簇的簇类中心向量。

式中x为第个样本点，Z为第号簇的样本点子集，N则代表第号簇中样本点的数量。

4）重复步骤2）和3），若簇类中心不再发生变化或达到迭代次数即终止。

对于待分类的个样本，1为第1个样本，样本集为={1,2, …,x…,x}。本文以监测数据流为原始数据，经过时间序列时间段划分共个时间段，度量各时间段间相似度值s。从而获得相似度聚类分簇样本集{1,2, …,s}。通过计算分簇样本与中心间的距离，按距离值进行分簇，获得不同的分簇结果。

1.4 正则化的极限学习机

ELM是一种简单有效的单隐层前馈神经网络学习算法[24]。该算法的隐含层权值和偏置是随机选择的，输出权值需要使用MoorePenrose广义伪逆来确定。给定一个样本数据集(x,t)，=1,2,…,，t为目标输出，则激活函数为()且包含个隐含层节点的标准ELM网络模型可以表示为

式中x=[x1,x2, …,x]T为第个输入样本，t=[t1,t2,…,t]T为目标输出，O表示输入x对应的网络输出，w=[w1,w2,…,w]T和b=[b1,b2, …,b]T分别为第个隐含层神经元与输入向量的权值，以及第个隐含层神经元的偏置。β=[β1，β2,…,β]T是第个隐含层节点和输出层节点的输出权值向量。因此，w·x表示w与x的内积，为了使t与O之间的误差最小，则式（4）可表示为

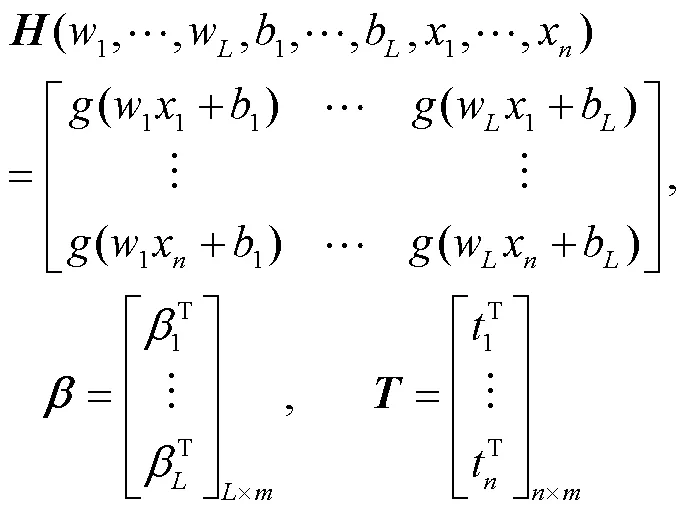
式中为隐含层神经元的输出矩阵，为输出权值矩阵，且传统ELM中的求解是一个简单的最小二乘问题，可以通过=T确定其值。H是的Moore-Penrose逆，当使用正交投影法时，则H=(T)-1T。

依据岭回归算法[25]原理，当ELM算法在计算时，若在T或T上加上参数1/，可以获得更好、更稳定的泛化性能，解决伪逆求解过程中数值不稳定的问题。因此，常使用正则化最小二乘法对ELM中的求解进行优化[26]，则式（5）可表示为

式中代表正则化参数，能够平衡正则化项和训练误差项。对式（7）进行求解中计算得到式（8）。

式中为单位矩阵。

2 预测模型实现

2.1 溶解氧浓度预测总流程

本文提出的基于相似时间段聚类机制的正则化极限学习机溶解氧预测模型，在分析天气条件相似性的基础上，探索溶解氧的昼夜变化特征，利用聚类机制，在分簇后的数据集中构建多个优化的ELM子预测模型，其预测总体流程如图2所示。

注：k为数据流聚类后获得的簇数，在各簇中对应得到k个预测子模型。

1）数据处理。本文的试验数据由水下传感器和自动气象站进行采集，在数据预处理模块中进行数据清洗和筛选。利用线性插值法对网络传输过程中丢失的数据进行插补，获得清洗后的数据流；再采用主成分分析法（principal component analysis, PCA）对影响DO浓度的指标因子进行关联分析，提取强影响因素。通过数据处理能够有效减少噪声数据带来的干扰，剔除冗余信息。

2）数据聚类。根据采集的天气数据流呈现的规律，对相似天气进行评估，量化时间序列的相似度，从而实现水体溶解氧数据流在相似天气条件下的聚类分簇。通过对溶解氧变化规律的探索，获取数据流特征，提高模型的预测精度。

3）构建预测模型。将聚类机制和正则化ELM神经网络应用到预测模型中，在不同的簇类中构建多个预测子模型。并通过不断训练预测模型，确定模型的最优参数信息和网络结构。

4）测试和分析。通过在测试数据集中进行试验，评估预测模型的性能。同时，选择不同的预测模型进行对比试验，验证本文提出的溶解氧预测模型的有效性和适用性。

2.2 数据处理

养殖生产中水体的感知监测节点经常会发生设备断电、故障等现象，使得采集的数据流不仅会丢失信息，还会产生很多噪声数据。为了解决这些问题，提高采集数据的质量，本文使用线性插值法对非连续丢失数据或连续丢失少于5个数据的数据流进行插补。若丢失数据为连续数据（5个及以上），则将天气环境指数作为参照信息，实现近似天气环境指数下的连续丢失数据替换。同时，采用熵权法对天气环境指数进行度量，基于空气温度、湿度、风速、风向、日照强度、光合有效辐射、辐射率等指标实现天气环境的综合评估。同时，监测系统采集的水质指标和天气环境指标对溶解氧浓度的影响程度均不相同，若使用所有因子作为预测模型的输入量，会影响预测模型的运行效率。为了降低预测模型的输入维度，减少预测运行时间，避免冗余信息的干扰，本文采用主成分分析法对各影响因子的重要性进行分析。

1,2, …,X分别对应各监测指标，则大小为的样本集则构成×的变量矩阵如下：

为了确定关键影响因子，首先需要对原始数据按照如式（10）进行标准化处理。

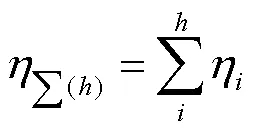
式中*为x*构成的数据矩阵；为r组成的相关系数矩阵；λ,η分别为相关矩阵的特征值和主成分贡献率；为个主成分的得分系数值；U×h为各主成分对应的特征向量，且=[1,2, …,u]。

2.3 数据聚类

为了实现对DO浓度的准确预测，本文对DO变化的潜在规律进行探索。由于溶解氧在监测时间内呈现较为规律的昼夜波动变化曲线，故图3仅列出溶解氧监测周期内的某一段连续5 d的变化曲线。从图3可以发现，溶解氧在养殖监测周期内，呈现明显的昼夜交替性变化，在每个19:00—06:00时间段（夜间）和06:00—19:00时间段（昼日）中均呈现相似的变化，但在每个时间段上的波动幅度仍有所区别。因此，结合数据采样的季节特征，本文在试验过程中将数据集按当季的昼夜时间点进行分割，并在分割后的数据集中构建多个预测子模型。本文将8 967个数据集分为126个时间序列数据流，这些数据流包括日间数据流和夜间数据流。事实上，这个时间序列的分割方式与整个养殖周期中的日出日落时间点相吻合，即所有日间数据流从06:00开始，到19:00结束，夜间数据流从19:00开始，到次日的06:00结束。

注：监测时间为2019年7月18日19:00至2019年7月23日18:50。

基于采样数据流的昼夜分割原则，获得DO数据流和对应天气指数的时间序列。利用FastDTW算法对时间序列相似度的量化结果，采用-means实现水体溶解氧数据流的相似度聚类。在-means聚类过程中，初始参数的选择直接影响整体聚类性能。为了评价选择的聚类数的聚类效果，利用常见的聚类有效性指标戴维森堡丁指数（davies bouldin score, DB）以及误差平方和（error sum of square, SSE）进行评估。DB为DB指数值，表示任意2个簇的平均距离之和除以2个簇中心之间距离的最大值。当DB值越小时，则簇内距离越小，簇间距离越大。SSE为聚类SSE值，代表簇内各点到簇中心距离的平方和，可以对聚类结果的松散度进行评估。SSE值越小则聚类效果越好越紧密。同时，肘部法则是一种目前被广泛应用于选择聚类数量的方法[27]。它主要利用SSE值来反映分簇的畸变程度，在变化曲线中能捕捉SSE值下降最大的位置对应的聚类数。一般来说，畸变程度最大的位置对应的簇数即为最优聚类数的值，DB与SSE指数的计算如下：

式中C和C分别表示第和第个簇，S和S分别表示C和C的紧凑度，d则表示C中心点z与C中心点z之间的欧式距离，φ表示第个簇C的重心。

2.4 预测性能测试与评估

本文利用均方根误差（root mean square error, RMSE）[1]、平均绝对误差（mean square error, MAE）[2]、纳什效率系数（Nash-Sutcliffe efficiency coefficient, NSE）[3]和运行时间（run time, RT）对预测模型的预测性能进行评价。RMSE和MAE可以从不同的数学角度反映预测性能的误差精度。RMSE和MAE值越低，表明模型越精确。NSE代表构建的预测模型的优劣。NSE值越接近1，表明模型的质量越好，预测能力越强。

3 结果与分析

3.1 关键因子筛选分析

本文采用PCA方法对8 967组试验数据的11个影响因子进行分析，按照式（12）～（16）计算其各因子特征值和方差贡献率，结果如表1所示。表1中5个主成分因子的累计贡献率已达86.136%，可由该5个主成分因子表征所有指标。旋转后的各主成分因子载荷矩阵结果见表2，该载荷结果值可体现各项指标与全部信息值之间的关系，载荷值的绝对值越大，表征的信息量则越大。

表1和表2结果显示主成分1的累计贡献率为34.188%，可表征光合有效辐射、日照和辐射率等因子。主成分2的贡献率为19.644%，可表征水温、气温等因子。主成分3的累计贡献率为14.29%，可表征湿度因子。主成分4的贡献率为10.83%，可表征CO2因子。主成分5的累计贡献率为7.184%，可表征pH值因子。基于上述结果，从而确定溶解氧预测模型的预测输入指标，包括光合有效辐射、日照、辐射率、水温、气温、湿度、CO2和pH值等8项指标。

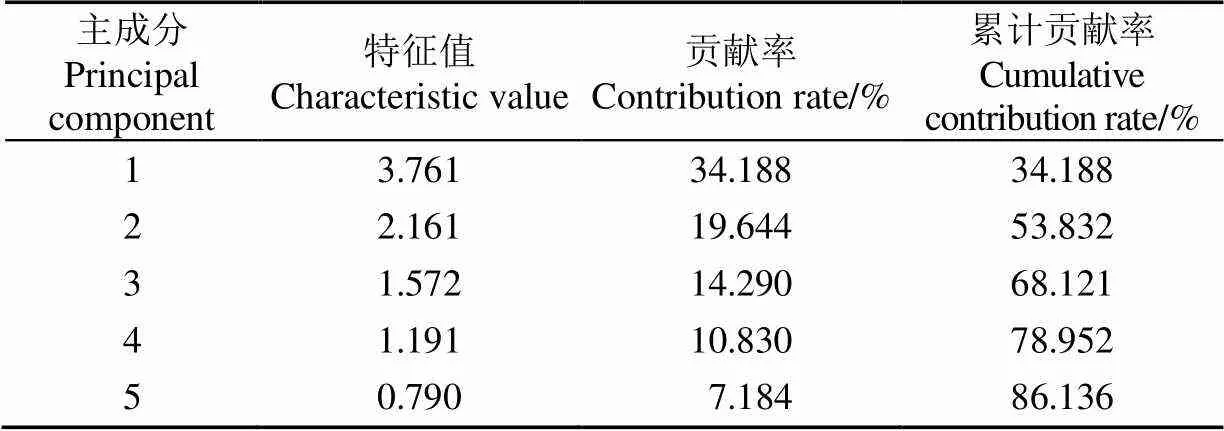
表1 特征值及方差贡献率

表2 主成分因子载荷矩阵

3.2 聚类结果分析

本文使用-means对分段后的时间序列进行相似度聚类，利用式（15）计算不同簇数的聚类评估指标DB值。同时，结合肘部法对聚类数进行二次筛选，利用式 （17）获得其SSE值的变化曲线，结果如图4所示。图4中，当=2时，其戴维森堡丁指数DB值为0.045 5，远低于取其他值时的DB值；当=4时，其对应的DB为次低值。同时，当值不断增大时，其对应的SSE指数呈现逐渐变小趋于稳定的状态。依据肘部位置法，可确定肘部位置的SSE值对应的理想聚类数。图4中不同聚类数的有效性指标SSE值变化明显，当3至=5时，SSE值下降速度变慢，在=4时形成sse值的肘部孤点。结合=4的聚类有效性指标DB=0.560 8，为次低值，因此，本文选择=4作为最优聚类数。

图4 簇数（k）与聚类指标关系

3.3 溶解氧预测性能评价

3.3.1 不同优化操作改进的ELM预测性能

基于时间序列相似度聚类后最佳簇类数为4，故本文构建的溶解氧预测模型包含4个预测子模型，并在不同的簇类样本中进行试验。每个预测子模型中溶解氧预测模型的输入量为8，输出量为1。隐含层节点数由经验法确定，在此基础上，最终得到各子预测模型的隐含层节点数分别为25，40，37和76，各簇类样本中的预测模型网络结构如表3。本文中所有预测模型的测试试验均基于Matlab R2014平台。

为了测试PCA关键因子筛选、-means相似时间序列聚类和正则化等操作对ELM模型的优化作用，本文构建-means-RELM (-means聚类优化后的RELM)、RELM、ELM模型作为对比预测模型。分别对PCRELM和这3个对比模型进行性能评估，各预测模型的试验数据样本相同，输入输出节点数相同，其溶解氧浓度预测效果如图5所示。

表3 不同簇中预测子模型的网络结构表

注：表中网络结构以“输入-隐含层节点-输出”的形式给出。

Note: Structure is given in the form of input-hidden layer node-output.

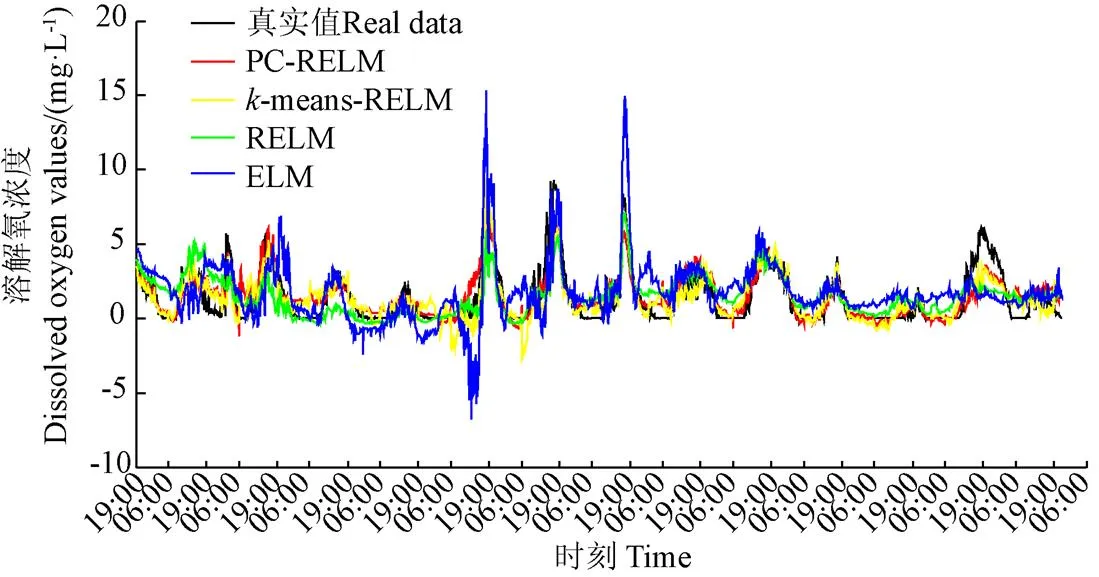
注：预测模型的测试时间为2019年8月27日19:00至2019年9月9日21:50。PC-RELM为基于主成分和聚类机制的改进正则化极限学习机模型。k-means-RELM为k-means聚类优化的改进正则化极限学习机模型。RELM为正则化极限学习机模型；ELM为极限学习机模型。下同。

图5中，4个预测模型都能获得较好的溶解氧预测效果，预测曲线逼近真实数据值。本文提出的PC-RELM和-means-RELM模型的溶解氧预测曲线在很多时刻上较为相似，预测结果更接近真实值。同时，RELM的预测曲线较ELM的预测曲线更接近真实值。由此可见，本文中，-means相似时间序列聚类操作和正则化优化操作能有效地提高溶解氧预测精度。

图6为不同ELM优化模型的预测误差，误差值为0作为零参照线。若一条曲线越接近零参照线，表明该曲线的预测误差越小，效果越优。图6显示，PC-RELM的预测误差曲线最接近零参照线，误差波动范围最小，-means-RELM的预测误差次之，波动幅度与PC-RELM较为接近，RELM的预测误差更次之，ELM的预测误差波动范围最大，与零参照线的偏离程度最大。由此可以判定，在测试样本集中，PC-RELM的预测误差最小，PCA关键因子筛选操作、-means聚类操作和正则化操作优化效果明显。同时，可以清晰地发现，除ELM模型的预测效果不稳定之外，其他各模型的预测误差均在每天的12:00－17:00波动幅度最大。事实上，这一时间段正是一天之中温度最高的时间。由于水温的时滞性，水体中水草等植物的光合作用在这一时间段最为活跃，持续时间更长，使得溶解氧自身变化更为复杂。另外，由于微生物、水草、残饵、残药等的附着，会使得传感器存在一定的数据漂移。因此在养殖生产中会选择5～6 d进行一次传感器的清洗和校准，进而影响数据采集的质量，而这一预测结果也正与实际的工作日志吻合。

图6 不同ELM改进模型的溶解氧预测误差

表4 不同ELM改进模型的溶解氧预测精度

表4为不同ELM改进模型的溶解氧预测精度，可以发现PC-RELM的预测结果评价指标RMSE和MAE值分别为0.9619和0.6941，明显低于其他2种模型。PC-RELM的RMSE值相比-means-RELM、RELM和ELM模型分别降低了5.75%、27.33%和43.10%。MAE值则相比较-means-RELM、RELM和ELM分别降低了5.42%、30.20%和47.21%。同时，PC-RELM方法的NSE值为0.712 8，比-means-RELM、RELM和ELM更接近1，且运行时间更短。-means-RELM方法与RELM方法比较，在各项预测精度指标和运行时间上均有较大程度的提高。上述结果表明，PC-RELM的预测精度和运行时间均具有一定的优势，PCA分析过程能有效提高运行效率，-means昼夜相似时间序列的聚类机制和正则化操作均能有效地提高模型的预测准确度。

3.3.2 多预测模型性能分析

为了验证本文提出的预测模型的优越性，本文将PC-RELM模型与现有的PLS-ELM（PLS优化ELM）[28]、LSSVM[9]和传统BP神经网络模型对测试时间内溶解氧的预测结果、预测误差和预测精度等进行比较。各模型的溶解氧浓度预测效果如图7所示。

注：PLS-ELM为偏最小二乘改进极限学习机模型。LSSVM为最小二乘改进支持向量机模型。BP为反向传播神经网络模型。

从图7可以看出，现有各模型的溶解氧预测结果较为一致。同时，图中PC-RELM的溶解氧预测曲线与真实值的趋势曲线的拟合效果较其他3种模型的预测曲线具有更高的一致性。PLS-ELM的溶解氧预测效果仅次于PC-RELM的预测效果，它的拟合程度与PC-RELM较为接近。预测效果更次之的是LSSVM预测模型，而BP神经网络的预测值与真实值差异较大。

图8 4个预测模型的溶解氧预测误差

图8为4个预测模型的溶解氧预测误差图。可以看出，PC-RELM的预测误差曲线最接近零参照线，其次是PLS-ELM，LSSVM和BP。LSSVM和BP模型的预测误差波动较大，PC-RELM在局部样本点上有一定幅度的波动，整体预测误差波动幅度较为稳定。事实上，图8中PC-RELM和PLS-ELM两模型的预测误差曲线波动趋势较为一致，说明这2个模型能有效地捕捉了溶解氧的潜在变化规律，呈现溶解氧变化特点。波动幅度较大的时间段主要集中在每天12:00－17:00，这一时间段温度较高，水生植物的光合作用也使得该时间段溶解氧波动更为明显。LSSVM和BP模型的预测误差较大，在各时间段内均有较大幅度波动，预测效果不佳。

表5 4个模型的溶解氧预测精度

表5为4种模型的溶解氧预测精度。可以看出PC-RELM的RMSE和MAE值分别为0.961 9和0.694 1，低于其他3种对比模型。PC-RELM的RMSE值分别比PLS-ELM、LSSVM和BP降低了41.54%、54.58%和67.16%，MAE值也分别降低了46.26%、59.98%和69.90%。在NSE指标上，PC-RELM的系数值更接近1，说明该模型具有较强的预测能力。同时，PC-RELM模型的运行时间比其他3种方法更短，表明该模型具有更高的预测效率。

结果表明，基于不同的优化操作构造的PC-RELM溶解氧预测模型是可行有效的。该模型通过时间序列的聚类机制获得了较高的预测精度，实现了溶解氧浓度稳定的预测。同时模型的整体运行效率较高，在同类预测模型中具有一定的优势。

4 结 论

本文考虑外部天气条件对溶解氧的影响以及溶解氧自身的昼夜变化特征，对养殖水体数据流进行分析，提出一种基于相似时间段聚类机制的正则化ELM溶解氧预测模型PC-RELM。主要结论如下：

1）使用PCA方法筛选影响溶解氧浓度变化的关键因子，降低预测模型的输入维度。从外部天气条件和溶解氧昼夜变化的角度，定义和量化天气环境指数，结合FastDTW完成基于天气环境指数的昼夜时间序列相似度的度量，克服常用欧式距离和传统DTW算法相似度计算的局限性。

2）采用-means方法完成相似度时间序列的聚类，将具有相似变化趋势的样本聚集在一起，捕捉昼夜时间下溶解氧变化的潜在规律，提高溶解氧预测准确度。

3）将PC-RELM模型的溶解氧预测结果与PLS-ELM、RELM和ELM模型的预测结果进行对比，其评估指标显示，PC-RELM模型的NSE系数为0.712 8，远远高于PLS-ELM、RELM、ELM、LSSVM和BP模型。PC-RELM模型的预测精度MAE值为0.694 1，亦明显优于其他模型，且运行效率较高，可见PC-RELM预测模型具有一定优势。

本文提出的溶解氧预测模型获得了较好的预测精度，能够为精准水质调控提供理论依据，具有一定的研究和推广价值。今后，我们将对水产养殖水体参数的预测预警进行更深入的研究，并将理论应用到生产实践中。

[1] 陈英义，成艳君，杨玲，等. 基于改进深度信念网络的池塘养殖水体氨氮预测模型研究[J]. 农业工程学报，2019，35(7)：195-202.

Chen Yingyi, Cheng Yanjun, Yang Ling, et al. Prediction model of ammonia-nitrogen in pond aquaculture water based on improved multi-variable deep belief network[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(7): 195-202. (in Chinese with English abstract)

[2] 曹守启，周礼馨，张铮. 采用改进长短时记忆神经网络的水产养殖溶解氧预测模型[J]. 农业工程学报，2021，37(14)：235-242.

Cao Shuoqi, Zhou Lixin, Zhang Zheng. Prediction model of dissolved oxygen in aquaculture based on improved long short-term memory neural network[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(14): 235-242. (in Chinese with English abstract)

[3] Cao X K, Liu Y R, Wang J P, et al. Prediction of dissolved oxygen in pond culture water based on K-means clustering and gated recurrent unit neural network[J]. Aquacultural Engineering, 2020, 91: 1-10.

[4] Ahmad S, Khan I H, Parida B P. Performance of stochastic approaches for forecasting river water quality[J]. Water Research, 2001, 35(18): 4261-4266.

[5] Palani S, Liong S Y, Tkalich P. An ANN application for water quality forecasting[J]. Marine Pollution Bulletin, 2008, 56(9): 1586-1597.

[6] Najah A, El-Shafie A, Karim O, et al. An application of different artificial intelligences techniques for water quality prediction[J]. International Journal of Physical Sciences, 2011, 6(22): 5298-5308.

[7] Ahmed M H, Lin L S. Dissolved oxygen concentration predictions for running waters with different land use land cover using a quantile regression forest machine learning technique[J]. Journal of Hydrology, 2021, 597: 1-12.

[8] 张阳，冼慧婷，赵志杰. 基于空间相关性和神经网络模型的实时河流水质预测模型[J]. 北京大学学报：自然科学版，2022，58(2)：337-344.

Zhang Yang, Xian Huiting, Zhao Zhijie. Real-time river water quality prediction model based on spatial correlation and neural network model[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2022, 58(2): 337-344. (in Chinese with English abstract)

[9] Liu S, Xu L, Jiang Y, et al. A hybrid WA-CPSO-LSSVR model for dissolved oxygen content prediction in crab culture[J]. Engineering Applications of Artificial Intelligence, 2014, 29: 114-124.

[10] Hua L, Zhang C, Peng T, et al. Integrated framework of extreme learning machine (ELM) based on improved atom search optimization for short-term wind speed prediction[J]. Energy Conversion and Management, 2022, 252: 1-18.

[11] 匡亮，华驰，邓小龙，等. 一种优化极限学习机的果园湿度预测方法[J]. 传感技术学报，2019，32(3)：418-423.

Kuang Liang, Hua Chi, Deng Xiaolong, et al. The oorchard humidity prediction method based on optimized extreme learning machine[J]. Chinese Journal of Sensors and Actuators, 2019, 32(3): 418-423. (in Chinese with English abstract)

[12] Zhang J, Xu F, Zhang Y, et al. ELM-based driver torque demand prediction and real-time optimal energy management strategy for HEVs[J]. Neural Computing and Applications, 2019, 32(3): 1-19.

[13] Huang Y, Li S, Li J, et al. Spectral diagnosis and defects prediction based on ELM during the GTAW of AI alloys[J]. Measurement, 2019, 136: 405-414.

[14] Udmale S S, Singh S K. Application of spectral kurtosis and improved extreme learning machine for bearing fault classification[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(11): 4222-4233.

[15] 陆慧娟，安春霖，马小平，等. 基于输出不一致测度的极限学习机集成的基因表达数据分类[J]. 计算机学报，2013，36(2)：341-348.

Lu Huijuan, An Chunlin, Ma Xiaoping, et al. Disagreement measure based ensemble of extreme learning machine for gene expression data classification[J]. Chinese Journal of Computers, 2013, 36(2): 341-348. (in Chinese with English abstract)

[16] 席磊，何苗，周博奇，等. 基于改进多隐层极限学习机的电网虚假数据注入攻击检测[J]. 自动化学报，2022，48：1-10.

Xi Lei, He Miao, Zhou Boqi, et al. Research on false data injection attack detection in power system based on improved multi layer extreme learning machine[J]. Acta Automatica Sinica, 2022, 48: 1-10. ( in Chinese with English abstract)

[17] 孙娜，周建中. 基于正则极限学习机的非平稳径流组合预测[J]. 水力发电学报，2018，37(8)：20-28.

Sun Na, Zhou Jianzhong. Hybrid forecasting model for non-stationary runoff based on regularized extreme learning machine[J]. Journal of Hydroelectric Engineering, 2018, 37(8): 20-28. (in Chinese with English abstract)

[18] Cao W, Huan J, Liu C, et al. A combined model of dissolved oxygen prediction in the pond based on multiple-factor analysis and multi-scale feature extraction[J]. Aquacultural Engineering, 2019, 84: 50-59.

[19] 宦娟，曹伟建，秦益霖，等. 基于游程检测法重构集合经验模态的养殖水质溶解氧预测[J].农业工程学报，2018，34(8):220-226.

HUAN Juan, CAO Weijian, QIN Yilin, et al. Dissolved oxygen prediction in aquaculture based on ensemble empirical mode decomposition and reconstruction using run test method[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(8):220-226. ( in Chinese with English abstract)

[20] 刘成菊，林立民，刘明，等.一种基于DTW-GMM的机器人多机械臂多任务协同策略[J].自动化学报，2022， 48(9):2187-2197.

LIU Chengju, LIN Limin, LIU Ming, et al. A multi-task collaborative strategy for multi-arm robot based on DTW-GMM[J]. Acta Automatica Sinica, 2022, 48(9): 2187-2197. ( in Chinese with English abstract)

[21] 姬文江，左元，黑新宏，等. 基于FastDTW的道岔故障智能诊断方法[J]. 模式识别与人工智能，2020，33(11)：1013-1022.

Ji Wenjiang, Zuo Yuan, Hei Xinhong, et al. An intelligent fault diagnosis method based on FastDTW for railway turnout[J]. Pattern Recognition and Artificial Intelligence, 2020, 33(11): 1013-1022. (in Chinese with English abstract)

[22] 陈莉婷，郑晶，高建清，等. 基于FastDTW案例检索的台风灾害应急方案生成[J]. 中国安全科学学报，2022，32(4)：171-176.

Chen Liting, Zheng Jing, Gao Jianqing, et al. Generation of typhoon emergency response plan based on FastDTW case retrieval[J]. China Safety Science Journal, 2022, 32(4): 171-176. (in Chinese with English abstract)

[23] 孙勇，谭文安，金婷，等. 基于在线聚类的协同作弊团体识别方法[J]. 计算机研究与发展，2018，55(6)：1320-1332.

Sun Yong, Tan Wenan, Jin Ting, et al. A collaborative collusion detection method based on online clustering[J]. Journal of Computer Research and Development, 2018, 55(6): 1320-1332. (in Chinese with English abstract)

[24] Huang G, Huang G B, Song S, et al. Trends in extreme learning machines: A review[J]. Neural Networks, 2015, 61: 32-48.

[25] 郭恒亮，李晓，付羽，等. 基于核岭回归算法的PROSAIL模型反演高空间分辨率叶面积指数[J].草业学报，2022，31(12)：41-51.

GUO Hengliang, LI Xiao, FU Yu, et al. High-resolution leaf area index inversion based on the kernel ridge regression algorithm and prosail model[J]. Acta Prataculturae Sinica, 2022, 31(12):41-51. ( in Chinese with English abstract)

[26] Heeswijk M, Miche Y. Binary/ternary extreme learning machines[J]. Neurocomputing, 2015, 149: 187-197.

[27] Bholowalia P, umar A. EBK-Means: A clustering technique based on elbow method and K-Means in WSN[J]. International Journal of Computer Applications, 2014, 105(9): 17-24.

[28] Shi P, Li G H, Yuan Y M, et al. Prediction of dissolved oxygen content in aquaculture using clustering-based softplus extreme learning machine[J]. Computers and Electronics in Agriculture, 2019, 157: 329-338.

Data stream prediction model for dissolved oxygen in aquaculture water using PC-RELM

SHI Pei1,2, KUANG Liang3, WANG Quan1,2, YUAN Yongming4

(1.,214105,; 2.,214105,; 3.,,214153,; 4.,,214081,)

Dissolved oxygen (DO) is one of the most important parameters for the water quality in aquaculture water. Long-term low oxygen environment can dominate the growth and reproduction of fish. Hypoxia can also cause large areas of fish death. Accurate and efficient DO prediction and control strategies can improve aquaculture production efficiency for the fewer aquaculture risks. However, an effective DO prediction has always been a tough challenge in aquaculture, due to the interference of external weather and the DO complexity. Multi-source or single sensors are generally used to build the prediction models, without considering the DO characteristics under similar weather conditions. Particularly, there is an outstanding diurnal variation in the DO content. Moreover, some redundant data can be collected from the water quality sensors in automatic weather stations. In this study, the principal component analysis and clustering method optimized regularized extreme learning machine (PC-RELM) was proposed to realize the DO prediction, considering the influence of external weather conditions on the DO and the diurnal variation. Firstly, the principal component analysis (PCA) was applied to determine the most influencing factors on the DO concentration, and reduce the data dimension of the prediction model for the high efficiency of prediction; Secondly, the entropy weight method was utilized to calculate the weather environment index at different time points. Fast dynamic time warping (FastDTW) was used to measure the similarity of weather environment in the time series data streams; Then, the-means algorithm was used to cluster the similarity of the time series using the weather environment index. And the sub-prediction models of regularized extreme learning machine (RELM) were constructed using the clustered datasets to forecast the DO concentration. Finally, the PC-RELM model was applied to the intelligent control process of DO in the aquaculture pond of the Wuxi Nanquan experimental base. The test results showed that the root-mean square error (RMSE) of PC-RELM prediction was 0.961 9, which outperformed the partial least squares optimized ELM (PLS-ELM), Least Square Support Vector Machine (LSSVM), and BP algorithms by 41.54%, 54.58%, and 67.16%, respectively. The mean square error (MSE) value of PC-RELM was 0.694 1, which outperformed the PLS-ELM, LSSVM and BP algorithms by 46.26%, 59.98%, and 69.90%, respectively. Meanwhile, the Nash-Sutcliffe efficiency coefficient of PC-RELM was 0.712 8, which was much higher than the rest prediction. In addition, the PC-RELM presented a high running speed of 0.316 2 s. The efficiency of PC-RELM was improved by about 7, 10, and 40 times, respectively, compared with the PLS-ELM, LSSVM, and BP. The improved model can be expected to extract the change patterns of DO under different weather conditions, indicating high prediction accuracy and efficiency. The finding can provide high-quality data and theoretical support for the precise control of DO in the pond water.

dissolved oxygen; aquaculture; water quality; clustering; fast dynamic time warping; regularized extreme learning machine

2023-01-05

2023-03-25

江苏省高校自然科学研究面上项目（21KJB520020）；无锡市“太湖之光”科技攻关项目（K20221044）；国家自然科学基金项目（62072216）；南京信息工程大学滨江学院人才启动经费资助项目（2021r038）；江苏省教育科学“十四五”规划2021年度课题（B/2021/01/15）

施珮，博士，讲师，研究方向为农业物联网和大数据分析。Email：njxk_sp@163.com

10.11975/j.issn.1002-6819.202301014

TP39; TP212; TP274.2

A

1002-6819(2023)-07-0227-09

施珮，匡亮，王泉，等. 基于PC-RELM的养殖水体溶解氧数据流预测模型[J]. 农业工程学报，2023，39(7)：227-235. doi：10.11975/j.issn.1002-6819.202301014 http://www.tcsae.org

SHI Pei, KUANG Liang, WANG Quan, et al. Data stream prediction model for dissolved oxygen in aquaculture water using PC-RELM[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2023, 39(7): 227-235. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.202301014 http://www.tcsae.org