一种 FOA-ELM 风速预测技术优化与仿真试验

许慧青 李程雄

摘要：为提高极限学习机的短期风速预测精度，提出一种果蝇算法优化ELM 的风电场短期风速预测模型。在保证ELM 预测误差最小的情况下，运用FOA 算法对ELM 模型的初始权值和隐含层偏置进行自适应选择，实现风电场短期风速的高精度预测。选择 EUNITE 数据集为算例分析对象，与 ELM、DE-ELM、GA-ELM 和 PSO-ELM 相比，FOA-ELM 具有更高的预测精度和更少的寻优时间，为风电场短期风速预测提供了新的方法和研究方向。

关键词：风速预测；果蝇优化算法；粒子群算法；技术优化；仿真

中图分类号：TP391.9文献标志码：A文章编号：1001-5922（2023）05-0130-05

Optimizationandsimulationof aFOA-ELMwindspeed predictiontechnique

XU Huiqing，LI Chengxiong

（Guangdong Energy Group Science and Technology Research Institute Co.，Ltd.，Guangzhou 510630，China）

Abstract：In order to improve the short-term wind speed prediction accuracy of extreme learning machine，FruitFly Optimization Algorithm was proposed to optimize ELM for the short-term wind speed prediction model of windfarm. Under the condition of ensuring the minimum ELM prediction error，the FOA algorithm is used to conductadaptive selection for the initial weight and hidden layer bias of the ELM model，so as to realize the high-precisionpredictionof thewindfarm'sshort-termwindspeed. ComparedwithELM，de-elm，GA-ELMandPSO-ELM， FOA-ELM has higher prediction accuracy and less optimization time，which provides a new method and research di? rection for short-term wind speed prediction of wind farms.

Keywords：Short-Term Wind Speed Forecasting；Wind Power；Fruit Fly Optimization Algorithm；Particle Swarm Optimization；Extreme Learning Machine

由于风速直接影响风电场的输出功率，因此对风电场风速进行预测，可以实现风电场输出功率和其波动性特性的预测，有利于缓解电力系统调峰压力，控制电力系统旋转备用容量，从而提高电力系统接纳风电的能力。

目前风速预测方法主要分为物理方法[1]和统计方法，物理方法主要通过气象信息和空间相关特性进行风速预测，该方法适合复杂地形区域的风速预测，不用采集大量实测风速数据，但存在预测精度较低的缺点。统计方法主要有时间序列法[2]、小波分析法[3]、卡尔曼滤波法[4]、神经网络法[5]等，与物理方法相比较，该方法具有预测精度高，但需采集大量历史数据，且模型参数的选择对预测较为敏感。

针对传统神经网络存在结构复杂、泛化能力弱和学习时间长的缺点，在传统神经网络的基础上提出极限学习机（ELM）。该方法具有很强的自主学习和自适应能力特点，通过随机赋予输入权值和隐含层偏置，运用最小二乘法求解出输入权值，极大地提高了泛化能力和训练速度，目前被广泛地应用于数据数据、故障诊断和图像分割等领域；但是，由于ELM 模型的输入权值和隐含层偏置是随机产生的，因此不能保证训练出的ELM模型具有最优的特点，并且存在收敛速度慢的缺点[6]。针对这些问题，有学者提出粒子群算法的极限学习机[7]；一种蝙蝠算法优化 ELM 的模拟电路故障诊断方法[8]；一种基于差分进化算法改进ELM 的电能质量扰动信号分类研究，虽然取得了一定成果，但这些方法容易出现早熟、陷入局部最优等问题[9]。当前，在参数最优方面，模式识别、图像分割和数据挖掘等领域已普遍采用果蝇算法（FOA）[10-13]。为提高 ELM 模型的短期风速预测的精度，针对ELM 模型性能受其初始权值和隐含层偏置的影响，建立一种新的 FOA-ELM 短时风力预报方法，通过 FOA 方法自动选取 ELM 中的初值及隐含层偏差，提高预报准确率。

1 果蝇优化算法

FOA的步骤表示为：

Step 1：设置 FOA 算法的参数并对其进行初始化：将果蝇种群设置为 N、最大迭代次数 T，将果蝇种群的初始化点设置为：（Xbegin，Ybegin）；

Step 2：计算果蝇个体位置：

xi =Xbegin + Valuex rand（）（1）

yi = Ybegin + Valuex rand（）（2）

式中：xi 、yi为果蝇个体i时刻的位置；Value 为果蝇的搜索距离。

Step 3：根据气味的浓度，确定果蝇与其座标之间的间距si；

Step 4：按照式（5），对果蝇幼虫进行个人适合度的推算；

Smell i = Function（si）（5）

Step 5：寻找并输出一个最优的风味浓缩量Smellb以及一个最优的定位（Xb. Yb）；

Step 6：使Smellbest= Smellb，使该群在最好的方位上进行飞行优化；

Step 7：假定当前位置的风味浓度为si，在前一位置的风味浓度为si一1的情况下，重复 Step 2～ Step 5；如果si>si一1，那么Step 6被执行。

2 极限学习机

ELM 与常规的神经网络比较，其优势在于其训练的时间更短，并且比较容易进行运算[14]；该ELM 的模型构造如图1所示。

假定存在 N个训练样品（Xi . Ti），Xi =[xi 1.xi2.…，xin]T eRn为输入向量，Ti =[ti 1. ti2.…. tin]T eRm为目标向量，X、T分别是nx Q 和 mx Q 的阵列，Q 为训练样本数量。于是，具有 L 个隐藏层的神经元的 ELM的输出可以被表达为[15-18]：

式中：Wi =[wi 1.wi2.….win]T 表示输入权；gi表示输出权；bi 表示第1个隐含层结点的偏差；g（x）表示激发函数；Wi .Xj分别为 Wi 和Xj的内部积。ELM 模型以使式（7）中的错误最小为学习目的。

由式（6）、式（7）可知，即存在一组参数gi、Wi 和 bi 使得式（8）成立。

式（8）的矩阵形式为：

式中：H 为输入端；g 为输入端的权值。

通过解式（9），可以获得输出层权重矩阵的估算值，从而获得输出层权重矩阵的最小二乘解 g（刈）：

3 基于FOA-ELM预测模型

ELM 模型性能受其初始输入权值和隐含层偏置的影响，由于ELM 模型的初始输入权值和隐含层偏置是随机产生的，不能保证训练出的ELM 模型是最优的，并且存在收斂速度慢的缺点。为提高ELM 模型的预测精度，运用FOA 算法的全局寻优和快速搜索能力对ELM 模型的初始输入权值和隐含层偏置进行自适应优化选择[19-20]，适应度函数为：

式中：tj为 ELM 模型的第 j 个实际输出值；Oj为 ELM模型的第 j 个预测输出值。

基于FOA-ELM 的短期风速预测算法的流程可具体描述为：

Step 1：将实测的风场资料分成2部分：一部分作为构建 FOA-ELM 模式的训练场，另一部分作为对 ELM模式的检验；

Step 2：设定FOA算法的最大迭代次数T，种群大小N，根据ELM初始权值和隐含层偏置值的取值上下限初始化果蝇种群。其中，We [-1，1]，b e [-1，1]；

Step 3：把所得到的培训集合引入到 ELM 中，根据式（12），求出每个果蝇幼虫的最佳适合度，并求出每个果蝇幼虫的最佳适合度；

Step 4：更新果蝇群体的位置；

Step 5：在调整了位置后，计算出适合度，并对果蝇群进行调整；

Step 6：如果当前迭代次数 t> T ，则保存最优解。否则 t = t+1，转到Step 4；

Step 7：输出ELM模型的最优参数，将最优初始权值和隐含层偏置带入ELM模型进行短期风速预测。

4 仿真试验

4.1 数据来源

选择欧洲智能技术网络（EUNITE）组织[8]提供的短期风速数据为研究对象，用于验证FOA-ELM 短期风速预测模型的效果。将不同时刻的风速数据看成时间序列{M（t ）. t =1.2.….n}，其预测模型可以描述为：

式中：o 为非线性函数；p 为风速预测窗口的宽度。文中风速预测窗口的宽度 p =3，也就是运用第 t 一1时刻、第 t 一2时刻和第 t 一3时刻的风速预测第t 时刻的风速，其预测原理图如图2所示。

ELM 模型的输入样本和输出样本构造情况结果如表1所示。

为提高 ELM 模型的运算效率和风速预测的精度，运用最大最小法归一化处理数据：

式中：xmin、xmax分别为风速时间中的最小风速和最大风速。

4.2 评价指标

选取平均绝对误差（MAE）和平均绝对误差（MAPE）来评估短时风力预报的有效性：

式中：yi为第i个时刻的实际风速；xi 为第i个时刻的预测风速；N 为预测样本数量。

4.3 仿真结果

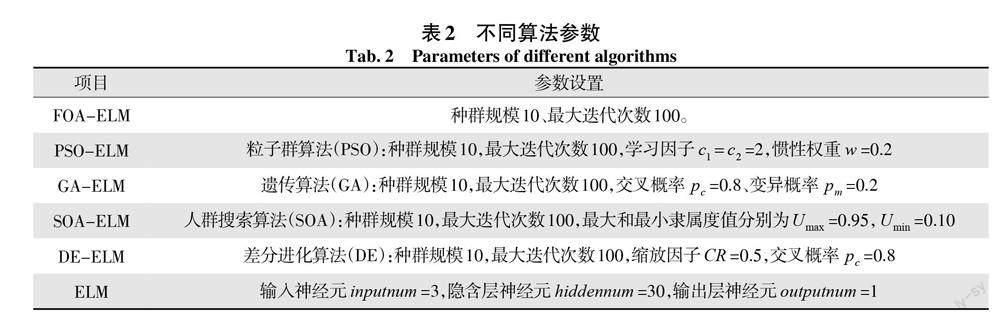
为说明 FOA-ELM 预测短期风速的效果，将 EUNITE 组织提供的144组短期风速时间序列进行预处理，设定风速预测窗口的宽度 p =3，处理获得141组风速数据。将141组风速数据分为训练集和测试集，其中前97组数据为训练集，最后，将44个资料作为试验资料，以检验该模式的有效性。为了更好地发挥 FOA-ELM 风力预报模式的优点，将其与 PSO-ELM、GA-ELMs、SOA-EMs、DE-OLMs 和 ELM 相比较，各方法的参数设定如表2所示；显示的短期风力预报的效果，具体如图3～图8所示。

从图3～图8及表3可以看出：（1）与 ELM、 DE-ELM、SOA-ELM、GA-ELM 和PSO-ELM 相比较，FOA-ELM模型的短期风速预测精度最高，高达2.20%，较 ELM 模型的7.31%，提高了5.11%。（2）DE-ELM、SOA-ELM、GA-ELM、PSO-ELM 和 FOA-ELM 的短期风速预测精度优于 ELM 模型，主要因为 DE、 SOA、GA、PSO 和 FOA 等算法优化选择了 ELM 模型的初始输入权值和隐含层偏置等参数，有效提高了 ELM 模型进行短期风速预测的精度。（3）从运行时间上看，除 ELM 模型之外，FOA-ELM 短期风速预测模型所耗费的运行时间最少。（4）由图9收敛速度对比图可知，FOA 较 DE、SOA、GA 和 PSO 算法的效果更好，具有更快的收敛速度以及更低的适应度。

5 结语

为提高极限学习机的短期风速预测精度，针对 ELM 模型性能受其初始输入权值和隐含层偏置的影响，提出一种基于果蝇算法优化 ELM 的风电场短期风速预测模型。选择 EUNITE 数据集为算例分析对象，采用RMSE、MAPE 和MAE 作为实验结果的评价指标，与ELM、DE-ELM、GA-ELM 和PSO-ELM 相比，FOA-ELM 模型的短期风速预测精度最高，达2.2%，较 ELM 模型的7.31%，提高了5.11%。 FOA-ELM 短期风速预测模型所耗费的运行时间更少。FOA-ELM 具有更高的预测精度和更少的寻优时间，为风电场短期风速预测提供了新的方法。

【参考文献】

[1] 冯双磊，王伟胜，刘纯，等.基于物理原理的风电场短期风速预测研究[J].太阳能学报，2011，32（5）：611-616.

[2] 蔡凯，谭伦农，李春林，等.时间序列与神经网络法相结合的短期风速预测[J].电网技术，2008，32（8）：82-85.

[3] 王晓兰，王明伟.基于小波分解和最小二乘支持向量机的短期风速预测[J].电网技术，2010（1）：179-184.

[4] 陶生金，刘孟，何明，等.玻璃纤维复合材料风电叶片雷击损伤试验研究[J].粘接，2021，46（4）：60-63.

[5] 陈忠.基于BP 神经网络与遗传算法风电场超短期风速预测优化研究[J].可再生能源，2012，30（2）：32-36.

[6] 邹平，郑天祺，冯俊，等.支柱绝缘子表面污秽带电清洗剂的制备与清洗特性研究[J].广东化工，2017，44（1）：39-40.

[7] 顾明泉，陈煌，刘芳等.风电叶片二次合模用腹板粘接结构胶研究[J].粘接，2019，40（5）：17-24.

[8] 陈绍炜，柳光峰，冶帅.基于核极限学习机的模拟电路故障诊断研究[J].西北工业大学学报.2015，33（2）：290-294.

[9] 张卫辉，黄南天，杨金成，等.基于广义S 变换和DE-ELM 的电能质量扰动信号分类[J].电测与仪表，2015，53（20）：50-55.

[10]WEN T P. A new fruit fly optimization algorithm：Taking thefinancialdistressmodelasanexample[J]. Knowl? edge-Based Systems.2012（26）：69-74.

[11] 杜利珍，王运发，王震，等.基于果蝇算法的第二类装配线平衡问题[J].中国机械工程，2018，29（22）：69-73.

[12] 杨书佺，舒勤，何川.改进的果蝇算法及其在PPI 网络中的应用[J].计算机应用与软件，2014（12）：291-294.

[13] 杨帆，張文娟，孙剑伟等.通过振动信号判断机械设备故障方法研究[J].粘接，2020，41（4）：171-175.

[14] 郑晓龙，王凌，王圣尧.求解置换流水线调度问题的混合离散果蝇算法[J].控制理论与应用，2014（2）：159-164.

[15] 王雪峰.含有风电场和分布式光伏的微电网经济调度[J].粘接，2022，49（6）：191-196.

[16] 高彩云，崔希民，高宁.熵权遗传算法及极限学习机地铁隧道沉降预测[J].测绘科学，2016，41（2）：71-75.

[17] 刘志远，李杨扬，何一.超高海拔地区负切变现象主要成因初步探究[J].粘接，2019，40（7）：56-62.

[18] 王芳，续欣莹，阎高伟.基于自适应差分进化算法优化极限学习机的球磨机料位测量[J].仪表技术与传感器，2015（6）：143-145.

[19] 余胜威，曹中清.基于人群搜索算法的PID 控制器参数优化[J].计算机仿真，2014，31（9）：347-350.

[20] 李亮，汤进能，汪龙.双馈风机并网次同步振荡机理分析及控制措施[J].粘接，2022，49（11）：144-146.