静脉血液流动非线性双曲系统的基本波

杨月颖, 盛万成

(上海大学理学院, 上海 200444)

血液流动动力学是生物力学领域的重要研究课题, 具有重要的生理学意义. 血流异常可能会导致一些心血管疾病, 如静脉曲张、动脉粥样硬化等. 静脉血管和动脉血管是血液流动的重要管道. 在研究大中型动脉、静脉血管中的血液流动模型时, 通常将其类比于不可压缩流体在柔性薄管中的流动[1]. 本工作将考虑如下的血液流动系统[2]:

式中: A 表示血管的横截面积; ρ 表示血管的血液密度; u 表示血管的血流平均速度; p 表示血管的平均压力; K(x) 表示血管壁的材料性质.

由于静脉血管的高度非线性性, 对静脉血液流动的研究[3-6]相对较少. Spiller 等[3]研究了静脉血液流动2×2 系统的Riemann 问题, 并证明了静脉系统中不会出现血管完全坍塌的情况, 即静脉血管的横截面积始终满足A>0.

在动脉血液流动研究方面, Toro 等[2]研究了动脉血液流动系统的Riemann 问题. Han等[7-8]引入了L-M 曲线和R-M 曲线, 构造了3×3 动脉血液流动系统Riemann 问题的解.Sheng 等[9]构造了6×6 动脉血液流动系统Riemann 问题的解, 并利用整体熵条件解决了解的唯一性问题.

静脉血液流动系统与动脉血液流动系统很大的差别在于它们的压力-面积关系[10], 即

式中: pe表示平衡状态下血管受到的外部压力; A0表示平衡状态下血管的横截面积; m 和n均为常数, 且在动脉中有m =,n = 0, 在静脉中有m ≈10,n =[11]; K(x) 是一个与时间无关的量, 在动脉、静脉中分别满足

其中E(x) 表示弹性模量, ν 表示Poisson’s 系数, h0(x) 和r0(x) 分别表示平衡状态下血管壁的厚度和血管半径[3].

本工作主要研究静脉血液流动系统(1) 中基本波的情况. 在求解系统时, 会出现3 种不同的基本波——疏散波、激波和驻波. 利用特征分析的方法求解出波线满足的条件, 并对驻波的存在性进行了详细的讨论.

1 特征分析

考虑下面的拟线性偏微分方程, 即

式中: U =(A,u,K)T;

A(U) 有3 个特征值, 即λ1=u −c,λ2=0,λ3=u+c, 分别对应右特征向量, 即

由于会出现1-特征或3-特征与2-特征重合的情况, 因此系统(1) 不是严格双曲的. 定义声速线为

使得系统(1) 在声速线上是非严格双曲的, 在声速线外的区域中是严格双曲的.

引理1 声速线u=±c 是(A,u) 平面上的严格凸(凹) 函数, 如图1 所示.

图1 (A,u)平面上的声速线Fig.1 Sonic curves in (A,u) plane

证明 函数u=c 关于A 求导, 可得

u=c 的二阶导数为

1.1 疏散波

由于1-特征满足λ1=u −c 以及R1=(A,−c,0)T, 从而有

给定左状态UL=(AL,uL,KL), 系统(1) 的后向疏散波(1-疏散波) 为

给定右状态UR=(AR,uR,KR), 系统(1) 的前向疏散波(3-疏散波) 为

1.2 激波

激波是一类间断解, 需要考虑系统(1) 的Rankine-Hugoniot 条件和Lax 熵条件. 由Rankine-Hugoniot 条件可知, 系统(1) 中的第3 个方程满足

式中: [f] = fR−fL表示变量f 的跳跃; σ 表示间断速度. 如果σ = 0, [K] /= 0, 则间断速度消失, 出现驻波间断解. 如果[K] = 0, 系统退化为守恒型. 此时, 只包含两种类型的基本波——疏散波和激波, 可以得到系统(1) 简化的Rankine-Hugoniot 条件, 即

系统(1) 的Lax 熵条件为

给定左状态UL=(AL,uL,KL), 根据式(5) 和(6), 可以得到系统(1) 的后向激波(1-激波) 为

给定右状态UR=(AR,uR,KR), 系统(1) 的前向激波(3-激波) 为

1.3 驻波

当σ = 0,[K] /= 0 时, 方程组不能化为守恒形式, 出现驻波间断解, 也不能使用传统的Rankine-Hugoniot 条件. 驻波, 也称作驻波间断, 是一类不依赖于时间的解. 考虑下面的常微分方程组

因此, 有

由式(8) 可得

因此, 有

由于

因此, 可得定常系统(7).

2 驻波的存在性

由系统(7) 可知, 给定左状态UL=(AL,uL,KL) 和右状态的材料性质KR(常数), 则可通过驻波与左状态UL相连的右状态U =(A,u,KR) 满足关系

联立两个方程, 可得

定义下面的驻波曲线函数为

当Φ(A;UL,KR)=0 时, UL与U 可以通过驻波连接. 因此, 通过考虑函数Φ(A;UL,KR) 的值可以确定S0(UL) (与UL可以通过驻波相连的状态组成的集合) 的存在性.

2.1 驻波曲线的性质

首先, 对函数Φ(A;UL,KR) 求导, 得

式中:

由式(9) 可知, 若U =(A,u,KR) 可以通过驻波与给定的状态UL连接, 则U 满足

因此, 只需要考虑函数Φ(A;UL,KR) 在曲线(13) 上的值即可. 如果存在曲线(13) 上的一点U满足Φ(A;UL,KR)=0, 则U 和UL可以通过驻波相连.

引理2 曲线Au=ALuL和声速线u2=c2在(A,u) 平面上有且仅有一个交点.

证明 联立曲线Au=ALuL和u2=c2, 可得

因此,

定义函数

对函数Q(A) 求导, 得

可知, Q(A) 是严格单调增函数.

当A →0 时, 有Q(A) →−(ALuL)2< 0; 当A →+∞时, 有Q(A) →+∞. 因此, 当A>0 时, Q(A)=0 有且仅有一个解. 引理2 得证.

由式(12) 可得函数Φ(A;UL,KR) 有如下性质.

引理3 沿着曲线Au = ALuL, 当u2> c2时, Φ(A;UL,KR) 单调递减; 当u2< c2时,Φ(A;UL,KR) 单调递增. 此外, 函数Φ(A;UL,KR) 在曲线Au=ALuL和声速线u2=c2的交点Umin=(Amin,umin,KR) 处取到最小值Φ(A;UL,KR)min=Φ(Amin;UL,KR).

由引理2 和引理3 可知, 函数Φ(A;UL,KR) 沿着曲线Au=ALuL(随着A 的增大) 先减小后增大, 在声速线Γ(KR):u2=c2(K =KR) 上取到最小值. 因此, 可以得到定理1.

2.2 驻波解的存在性

本节将具体讨论存在驻波的区域, 是对定理1 的一个完善. 证明了在(A,u) 平面存在一个区域Ω, 使得当UL/∈Ω 时始终满足Φ(A;UL,KR)min≤0, 即UL存在驻波.

不失一般性, 本工作总是假设

同时, 基于引理4, 本工作只考虑uL>0 的情况.

引理4 由式(13) 以及A > 0 可知, 如果U = (A,u,KR) 与UL= (AL,uL,KL) 可以通过驻波连接, 则有sgn(u)=sgn(uL).

考虑函数(11) 在A=AL处的函数值, 可以得到

基于上述结论以及函数Φ(A;UL,KR) 的性质, 本工作将在定理2 中给出存在驻波的状态所在的区域.

定理2 对任意一个给定的左状态UL=(AL,uL,KL), 有: ①如果UL∈Ω, 则UL没有驻波; ②如果UL/∈Ω, 则UL有两个驻波; ③如果UL位于区域Ω 的边界上, 则UL有且仅有一个驻波,其中区域Ω 是由3 条曲线Γ+、Γ1−、Γ2−包围的区域,如图2 所示, 其中曲线Γ+、Γ1−、Γ2−将在证明中给出.

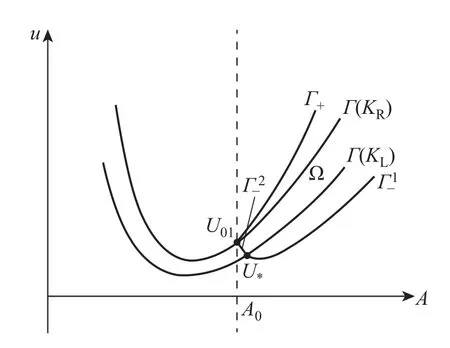
图2 区域ΩFig.2 Region Ω

证明 下面将分3 个部分证明定理2.

(1) 若AL< A0, 由式(16) 可知Φ(AL;UL,KR) < 0. 显然, 有Φ(A;UL,KR)min≤Φ(AL;UL,KR)<0 成立, 从而UL始终有两个驻波.

(2) 若AL= A0, 由式(16) 可知Φ(AL;UL,KR) = 0. 此时有Φ(A;UL,KR)min≤Φ(AL;UL,KR) = 0 成立, 从而UL至少有一个驻波. 由函数Φ(AL;UL,KR) 的单调性可知, 它的最小值是在声速线Γ(KR) 上取到的. 不妨设点U01= (A01,u01,KL) 是声速线Γ(KR) 与直线A=A0的交点, 则当UL=U01时, Φ(A;UL,KR)min=Φ(AL;UL,KR)=0.

(3) 若AL>A0, 由式(16) 可知Φ(AL;UL,KR)>0. 此时不能直接判断Φ(A;UL,KR)min的值, 需要进行更多的讨论. 假设是声速线Γ(KR) 上的一点. 若UL满足ALuL=,由引理3 可知,当0时,函数Φ(A;UL,KR) 单调递增, 且Φ(A;UL,KR)min=Φ(;UL,KR). 因此, 可以发现当UL∈Γ(KR)且AL>A0时, 有Φ(A;UL,KR)min>0. 由定理1 可知, UL没有驻波.

式中:

由式(18) 可知, 沿着曲线

图3 曲线Γ+Fig.3 Curve Γ+

定义曲线Γ(KL) : u = c(K = KL). 沿着曲线函数先增大后减小, 在曲线Γ(KL) 上取到最大值. 当AL→+∞时,因此, 对任意一个给定的都存在另外一个点使得= 0, 即U∗L只有一个驻波. 因此, 当= 0 始终有两个解.

综上, 可以得到

由式(21) 和(22), 可得

由曲线的定义可知: ①如果UL位于曲线Γ+、Γ1−、Γ2−包围的区域Ω 中时, UL没有驻波;②如果UL在区域Ω 外时, UL有两个驻波; ③如果UL在曲线Γ+、Γ1−、Γ2−上时, UL有且仅有一个驻波. 定理得证.

下面讨论曲线Γ+、Γ1−、Γ2−的一些性质.

定理3 曲线Γ+(A)(A ≥A0) 是单调递增的; 曲线Γ2−(A):u=u−(A)(A0≤A ≤A∗) 是单调递减的. 对任意给定的一点(A,u) ∈Γ1−, 曲线Γ1−在该点的斜率始终大于过该点的曲线Au=在该点的斜率, 且当

证明 曲线Γ+、Γ1−、Γ2−均满足下述关系:

因此, 可以用如下的参数方程表示曲线, 即

式中:

因此, 可得

此外, 曲线Γ+、Γ1−、Γ2−位于不同的区域中(见图2), 则分别有

令

则有

3 结束语

本工作研究了静脉血液流动非线性系统中的基本波. 由于系统的非严格双曲性, 特别讨论了驻波的存在情况. 定理2 证明了存在一个由3 条曲线包围的区域Ω, 使得当左状态位于区域Ω 外时, 存在与左状态相连的驻波. 因此, 确定了相平面上存在驻波的区域. 这对于分析静脉血液流动系统的Riemann 问题具有重要意义. 定理3 给出了3 条曲线的一些性质, 证明了图2 中对曲线的刻画是合理的. 后续将进一步研究系统(1) 的Riemann 问题.