工字组合梁横向分布系数计算与影响分析

李名泽

摘要 工字组合梁应用日益广泛，是否可以参照传统算法计算工字组合梁值得深入研究。文章以某高速改扩建桥梁为案例，对各片梁汽车荷载横向分布系数采用多种算法进行计算，结果表明可采用单梁模型来简化计算工字组合梁，与梁格法计算结果误差在10%以内；分析横梁布置与桥面板厚度对横向分布系数的影响，结果表明增设横梁和加厚桥面板对工字组合梁横向分布系数影响不明显。

关键词 工字组合梁；横向分布；梁格法

中图分类号 U441.2文献标识码 A文章编号 2096-8949（2023）10-0093-03

0 引言

将多主梁结构简化为单梁是常规装配式桥梁内力计算常采用的算法，通过假定各梁板之间的某种连接关系，计算出分配给各个梁板的汽车荷载。实践表明，这种近似假定不仅可以满足工程应用的精度需求，而且可以大大减少设计人员的计算工作量，广泛应用于桥梁电算。侯帆从横向分布系数、抗弯承载力计算方法等对钢混组合梁桥进行了深入研究[1]。闫林君等选取了不同情况下的钢混组合梁拟合出了此类桥梁荷载横向分布系数的计算公式[2]。代力等利用ABAQUS建立有限元模型研究了组合梁抗弯极限承载力的参数影响规律[3]。交通运输部2021年发布的《装配化工字组合梁桥通用图》[4]无30 m以下跨径组合，且只适用于双向四车道和六车道，适用范围受限制大。为了使适用范围更广泛，比如高速公路改扩建受限于净空要求、结构高度受限制较大的中小跨径桥梁，在考虑选取自重轻、跨越能力强、对环境影响还小的工字钢混组合梁桥梁方案时，是否可以参照装配式组合桥梁的内力计算方法求解工字钢混组合梁内力。依托浙江甬台温高速公路改扩建工程项目某上跨高速桥梁，根据多种横向分布系数计算方法求解，对比分析多种算法的结果，可为类似桥梁计算与设计提供参考。

1 工程概况

某上跨甬台温高速匝道桥其中一联为4×20 m预应力混凝土空心板，高速两幅分别从中间两孔下穿。现因甬台温高速改造，四车道改八车道，改扩建后高速路基宽度2×20.5 m，而老桥跨径仅为20 m，需将老桥拆除重建后才满足高速下穿需求。原有桥梁20 m空心板板厚90 cm，铺装层为10 cm调平层+8 cm沥青混凝土，净空略大于5 m，富余极小，因此改建方案敲定需综合考虑跨径和净空限制。

2 方案思路

老桥重建方案受限于老桥净空，同时为了尽可能地减少对现有老桥的影响，选择加大其上跨高速的两孔跨径，将其中4×20 m跨改为（17+23+23+17）m的跨径组合，桥梁结构高度不得大于100 cm（梁高90 cm+调平层10 cm），下部结构能利用的桥墩尽可能利用。

空心板、小箱梁、T梁及矮T梁是当前高速公路中小跨径常规桥梁常采用的上部结构形式[5]。

装配式预应力混凝土空心板桥的跨径不宜大于20 m，首先排除空心板方案[6]。由表1梁板结构高度可知，23 m小箱梁梁高按25 m跨小箱梁取为140 cm，23 m T梁梁高按25 m跨T梁取为170 cm，23 m矮T梁梁高按20 m跨矮T梁取为110 cm，结构高度均大于100 cm，因此，当前高速公路桥梁普遍采用的装配式上部组合结构形式无法满足该桥改扩建的要求。

此次在保证下穿道路净空的情况下，考虑自重轻、跨越能力强、对环境影响还小的钢结构桥梁方案，设计出符合此次改扩建要求的组合梁结构，组合梁厚度（工字钢结构高度+桥面板厚度）不得大于100 cm（老桥空心板板厚90 cm＋调平层10 cm）。钢-混凝土工字组合梁构造简单明了、力学受力上明确、施工难度低，不仅可以充分发挥钢材及混凝土各自的受力特性，而且还容易形成标准化，适用于标准化设计、工业化建造，一方面提高了结构建设效率，另一方面也保证了工程质量。

3 截面设计

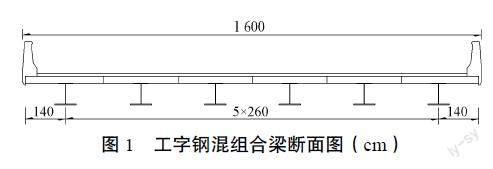
主梁截面尺寸拟定如图1。

采用多片“工字型钢梁+混凝土橋面板”的组合梁，钢混组合梁桥横断面一般由工字型钢主梁、横向连接系、剪力连接件，以及上部混凝土桥面板组成。工字型钢主梁通过横向连接构造进行连接，并通过剪力连接件与混凝土桥面板连接成整体共同受力。根据国内大量已有经验，简支结构的工字组合梁高跨比一般取1/15～1/22。该桥梁高拟定为1 m，计算跨径为22.22 m，高跨比为1/22.22略超出经验值范围。混凝土桥面板宽15.8 m，悬臂长1.4 m，C50桥面板等厚布置，厚0.25 m。单片Q355工字钢主梁梁高0.75 m，钢主梁中心间距2.6 m。

4 横向分布系数计算

杠杆法、刚性横梁法、刚接（板）梁法等是目前成熟、可靠的混凝土桥梁荷载横向分布系数简化算法。运用传统装配式桥梁横向分布系数计算方法（刚性横梁法、刚接板梁法及比拟正交异性板法[7]）进行计算，并将空间梁格法计算结果与几种传统算法的计算结果做比较分析。

传统的装配式混凝土桥梁，板梁是钢筋混凝土或者预应力钢筋混凝土材料，而工字组合梁是由钢材和混凝土两种不同性质的材料组合而成的非单一性质的梁。因此，如何求解截面特性是首要问题。在工字组合梁中，通常把混凝土截面等效成钢截面。可利用Midas Civil的组合截面直接获取组合梁截面特性[8]。

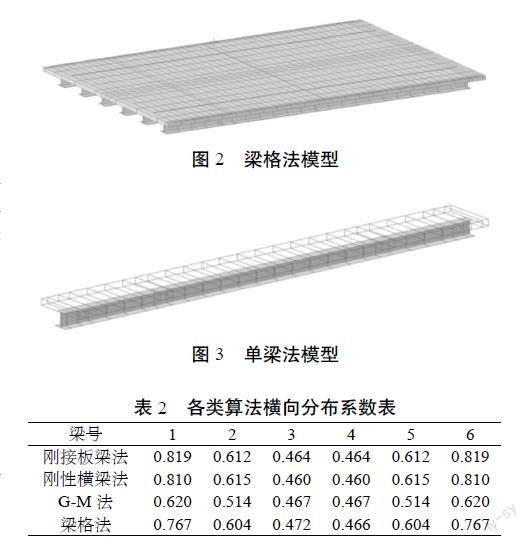
采用Midas Civil建立梁格法模型如图2和单车道单梁模型如图3，将梁格法模型和单梁模型的跨中挠度值提取出来，两者比值即为横向分配系数[9]。

式中，mi——第i片梁横向分布系数；fi——梁格模型下第i片梁跨中挠度；di——单车道单梁模型下第i片梁跨中挠度。

由表2可知刚接板梁法和刚性横梁法结果偏差极小，基本一致，都比梁格法结果大；G-M法计算结果偏小。刚接板梁法的边梁计算结果仅仅比刚性横梁法大1.1%，这说明即使忽略了横隔梁，桥面板的约束刚度也很强，已经接近刚性横梁法下“横梁是刚性的”假定，这也与当前钢混组合梁实际应用时减少横梁布置的习惯性做法相吻合。边梁和中梁采用刚接板梁法比梁格法计算结果分别偏大6.6%和1.3%，最大偏差不超过10%。因此，工程应用中可按照刚接板梁法计算汽车荷载横向分布系数。另外，对于此类多主梁的装配式结构桥梁，汽车活载的效应值一般本就比恒载效应值小，另外汽车活载效应值不到10%的差距对最不利荷载组合下效应的影响只会更小，因此总体考虑是偏于安全的。

5 组合梁横向受力分布影响因素分析

5.1 横向连接对横向分布系数的影响

采用Midas Civil建立不同道数横向连系梁的有限元模型与仅有端横梁模型对比分析来研究横梁布置对组合梁桥横向受力分布情况的影响。

由表3的计算结果可知，加密布置横梁可以降低横向分布系数，设置4道中横梁比仅设置端横梁时横向分布系数降低为边梁1.5%、中梁3.8%。

增设横梁的确可以增强整体性，但影响效果很小，并不能显著降低横向分布系数。在较少设置横隔梁的情况下，边、中梁横向分布系数降低不到5%。这说明工字组合梁桥的受力特点是桥面板承担大部分荷载作用，此结论也与实际工程少布置横向连系梁相吻合。

5.2 桥面板厚度对横向分布系数的影响

桥面板厚度影响工字组合梁结构刚度，更影响主梁间联系刚度，从而影响全桥内力分配。建立桥面板厚度分别为200 mm、250 mm、300 mm的三种模型，研究横向分析系数受桥面板厚度变化的影响规律[10]。

从表4可以看出，边、中梁汽车荷载横向分布系数随着桥面板从200 mm增厚到300 mm时仅仅降低8.8%、6.6%。

基于受力基本原理分析，随着桥面板厚度的增厚，桥面板截面的横向弯矩也随之增大，截面承载能力也增强。在保证结构安全的前提下，加厚桥面板直接加强了桥面板的刚度，从而增强梁片之间的横向联系，使各片主梁受力更加均匀。但是从上表结果对比可知加厚桥面板并不能达到显著降低横向分布系数的效果。而且，桥面板不可能无限加厚，因此在工字组合梁结构高度一定的情况下，选取合适的桥面板厚度对组合梁结构设计尤其重要。

5.3 主梁片数对横向分布系数的影响

建立8片主梁模型与6片主梁模型对比分析来研究主梁片数对组合梁桥横向受力分布情况的影响[11]。

由表5中计算结果可知，主梁片数的改变对边、中梁汽车荷载横向分布系数的改变是显而易见的，布置8片梁时边梁、中梁分别比布置6片梁时横向分布系数降低了31.5%、35.1%，降幅显著。

基于受力基本原理分析，梁片数越多，每片梁承担的荷载相对就小，也缩小了工字钢主梁间距，提高了梁与梁之间的抗扭约束刚度，增强了结构整体性，从而更均匀分摊荷载，边中梁横向分布系数差距也缩小了，受力更加均匀[12]。

6 结论

借鉴传统装配式组合梁桥汽车荷载横向分布计算方法研究了工字组合梁横向分布系数的计算，并采用梁格法加以对比分析，而后进行因素影响性分析，如横向连系梁布置、桥面板厚度和主梁片数的影响，得出以下结论：

（1）项目前期方案设计和初步设计阶段可以采用传统的单梁法对工字组合梁桥进行内力计算，即使有一定的误差，但仍然在工程项目可接受范围内，而且还是偏于安全的。在施工图阶段再采用梁格法进行精细化分析，此举可以大大节省设计工作量。

（2）边中梁汽车荷载横向分布系数随着桥面板从200 mm增厚到300 mm时仅仅降低不到10%，因此通过加厚桥面板来降低汽车荷载横向分布系数也是不太有效果的，设计时需合理选择桥面板厚度。

（3）增加设置横向连系梁并不能显著降低横向分布系数。计算结果表明在较少设置横隔梁的情况下，边梁横向分布系数降低不到5%。结合桥面板厚度分析可知，桥面板对工字钢的约束作用比横向连系梁影响大，工程实践应用中可以减少布置横向连系梁，不仅可以达到节省钢材的经济性考虑，还可以减少安装时长，缩短工期。

（4）增加主梁片数，明显缩减主梁间距，可以有效改变单片主梁受力分配，显著降低主梁汽车横向分布系数，实际工程应用时需结合经济性分析做优化设计。

参考文献

[1]侯帆. 钢混组合梁桥横向分布及抗弯承载力研究[D]. 南京：东南大学， 2019.

[2]闫林君， 张经伟， 罗奎. 装配式多主梁钢-混组合梁桥的荷载横向分布研究[J]. 公路交通科技， 2020（3）： 59-69.

[3]代力， 江祥林， 朱泽文， 等. 组合梁抗弯极限承载力参数影响分析[J]. 交通科技， 2021（2）： 20-24.

[4]装配化工字组合梁钢桥通用图： JTG/T 3911—2021[S]. 北京：中华人民共和国交通运输部， 2021.

[5]邵旭东. 桥梁工程[M]. 北京：人民交通出版社， 2007.

[6]公路鋼筋混凝土及预应力混凝土桥涵设计规范： JTG 3362—2018[S]. 北京：人民交通出版社， 2018.

[7]刘华， 叶见曙， 俞博， 等. 桥梁荷载横向分布系数计算方法[J]. 交通运输工程学报， 2009（1）： 62-66.

[8]聂建国. 钢-混凝土组合结构桥梁[M]. 北京：人民交通出版社， 2011.

[9]李瑞琪， 袁万城， 高康， 等. 装配式简支钢-混组合小箱梁桥荷载向分布系数的研究[J]. 结构工程师， 2015（4）： 54-59.

[10]石雪飞， 马海英， 刘琛. 双工字钢组合梁桥钢梁设计参数敏感性分析与优化[J]. 同济大学学报：自然科学版， 2018（4）： 444-451.

[11]章晗， 丁汉山. 多梁式钢-混组合弯箱梁桥荷载横向分布系数计算分析[J]. 特种结构， 2018（6）： 95-101.

[12]黄侨. 桥梁钢-混凝土组合结构设计原理（第二版）[M]. 北京：人民交通出版社股份 有限公司， 2017.