基于数学三种语言转化的概念教学
李武

【摘要】在高中数学概念教学中,通过数学三种语言转化设置实验操作、强化概念的多元表征、運用具象结合和数形结合策略,激发学生的学习兴趣,优化概念的知识结构,培养学生的概念探究能力和构图能力。
【关键词】数学三种语言转化;概念多元表征;具象结合
数学概念是人脑对现实对象的数量关系和空间形式的本质特征的一种反映形式,是一种数学的思维形式,是数学之本、解题之源。如果我们在学习的过程中没有对概念有着深刻的认识,透彻的理解和熟练掌握,那么在数学的学习过程中将会遭遇很多困难,甚至无法进行更深入的学习。但在现实的教学中由于受到应试教育的影响,很多教师把更多的时间放在解题技巧的传授上,而忽视了数学概念的重要性,认为概念只不过是一个定义,没有去深究它的内涵。
数学语言不是简单地描述数学知识,它更是数学思维的一种载体和教学过程的交流工具,数学三种语言包括文字语言、图形语言和符号语言。在传统的数学概念教学中通常是教师讲,学生被动地接受知识,忽略了学生在课堂教学中的参与性,限制了学生的思维发展和数学核心素养的培养。本文作者将结合自己的教学经历探讨数学三种语言转化融入数学概念教学中,对概念教学、学生思维培养、学生探究式学习方式及学生数形结合能力的培养都具有现实的教学意义。
一、设置探究操作实验,培养概念探究能力
随着课程改革的实施,传统的数学概念教学模式已经无法满足新课程标准的需要,所以数学概念课堂教学模式必须要做出转变。传统的数学概念教学注重直接从数学概念出发,教学的着重点是教师向学生分析概念的内涵和强调概念满足的条件和范围,虽然这样的概念教学具有严谨性,但这种只注重结果的教学使学生没有真正了解数学概念的本质,阻碍了学生探究知识的过程及思维的过程。可见传统的数学概念教学模式不适合新课程标准中培养学生数学核心素养的要求,在概念教学中通过数学三种语言转化设置探究性操作实验,既培养了学生对概念的探究能力,又实现了概念教学由“知识型”向“过程型”的转变。
案例一:“椭圆及其标准方程”教学片段。
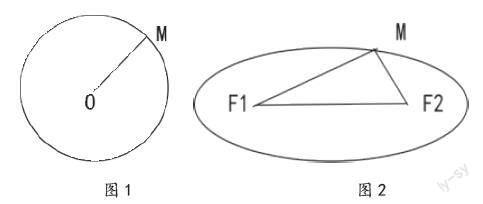
问题1:取一条定长的细绳r,把它的两端都固定在图板的同一点F,套上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点)M画出的轨迹是 ?
学生:通过文字语言的关系转化成图形语言,如图1。
问题2:观察上面实验操作得到的图形,用集合语言表示动点M的轨迹。
学生:{M||MF|=r}。
问题3:如果把细绳的两端拉开一段距离2a,分别固定在图板的两点F1,F2。套上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点)M画出的轨迹是?
学生:通过实验操作的文字语言转化成图形语言,如图2。
问题4:如何用集合语言表示动点的轨迹。
学生:{M||MF1|+|MF2|=2a>|F1F2|}
问题5:类比于圆方程的步骤—建、设、限、代、化,用方程表示动点M轨迹。
案例一是通过数学三种语言转化设置探究操作实验的概念教学,同时将类比推理的数学思想融入其中。案例中就是把数学中对象的相似性作为根据进行联想,从而将对某一数学对象的已知知识迁移到另一个相似的数学对象上,从而获得新的发现的思想方法。整个概念的呈现过程通过数学三种语言转化设置探究性实验达到教学的目的。概念教学不再是以往的由教师直接给出数学概念的教学模式,而是引导学生通过转化数学三种语言对问题进行探究的过程,体现了学生是信息的加工主体,整个教学过程让学生从原来的重“知识型”向“过程型”转变。案例中通过引导学生类比圆的方程实验,利用定线和笔尖按照某种定量关系画出轨迹,并引导学生通过实验操作观察如何将图形语言转化成符号语言。整个实验过程不仅体现了引导学生灵活掌握三种数学语言相互转化的教学理念,同时还体现了类比推理的数学思想。
数学的概念理论性强且抽象,通过三种语言转化设置探究性实验操作将新概念与学生原本掌握的概念进行类比,有效帮助学生理解概念、掌握规律,既提高了学生的学习兴趣,又降低了学生学习的难度。
二、强化概念多元表征,优化概念知识体系
数学概念的学习过程其实就是学生呈现原有知识再创造的过程。那么要实现学生再创造的方式就是教学由“传授型”向“探究型”转变,引导学生亲自参与概念的探究过程。在数学概念教学中,通过数学三种语言转化强化概念的多元表征,有助于学生对概念的掌握和深入学习,优化了数学概念知识结构的系统性,强化数学知识间的练习,进而形成完善的数学概念。
案例二:“全概率”教学片段。
引例1:从标有数字1、2、3、4、5的五张卡片中,依次抽出2张(取后不放回),你能否求出“第二次抽到的卡片是偶数”的概率?
问题1:如何用有序实数描述实验结果?
学生操作:
(1,2),(1,3),(1,4),(1,5)
(2,1),(2,3),(2,4),(2,5)
(3,1),(3,2),(3,4),(3,5)
(4,1),(4,2),(4,3),(4,5)
问题2:设事件A表示“第一次抽到奇数”,事件B表示“第二次抽到偶数”,用韦恩图表示事件A、A、B间的关系。
学生操作:
问题3:根据韦恩图如何用符号语言表示P(B),
学生:从图形语言转化成符号语言P(B)=P(AB)+
P(AB)=P(A)P(B|A)+P(A)P(B|A)高中全概率概念具有抽象性,其概念的表征方式也具有多样性。案例二通过数学三种语言转化将点集(树状法)、图像(韦恩图)及公式呈现全概率定义的三种表征达到了教学的目的。在概念教学过程中,引导学生探索全概率的三种表征方式可以让学生从不同的角度探究和理解全概率的含义,促进学生对全概率有“质”的理解。
三、具象结合,理解概念本质
概念学习的过程就是抽象化的过程,虽然数学概念本身比较抽象,但是数学概念的背景和生成是具体的,如果能在概念教学过程中利用数学三种语言转化将具体和抽象结合,通过概念探究过程了解概念的本质含义,则有效提高了数学概念的教学质量,达到高效教学的目的。
案例三:“函数的奇偶性”教学片段。
问题1:画出下列函数(x)=x2,如图3。
问题2:观察(x)=x2,填写函数值对应表。
问题3:(师生共探,抽象定义)。
问题4:(操作体会)请学生上来拖动图4坐标系中y轴右侧的点p,体会对于一个一般函数(x),若其图像关于y轴对称,如何用符号语言刻画?
根据数学概念本身的抽象性和概念生成过程的具体性特点,在概念教学过程中通过数学三种语言转化设置问题探索,能有效地将抽象概念具体化。案例三中的问题4借助网络画板呈现偶函数的图像特征,引导学生观察点p的实验特点,学生很容易从直观动画中得到偶函数条件中要满足的任意性和对称性,进而准确地用符号语言表示出偶函数的定义,达到概念课堂高效教学的目的。
四、数形结合,培养学生构图能力
数形结合是重要的数学思想,是学生学好数学必须要掌握的一种方法,在数学概念教学中通过转化三种数学语言引导学生构图已成为课堂教学重要的组成部分。在概念教学中,培养学生通过概念的数与形之间的关系去构图,能有效地将抽象概念具体化、形象化,不仅让学生更能直观地理解函数概念,还培养了学生的直观想象和构图能力。
案例四:“基本不等式”教学片段。
问题1:请同学们拿出课前准备的四张全等的等腰直角三角形(直角边用a、b表示,斜边用c表示,其中a=b),将四个等腰直角三角形摆放成一个正方形,并观察直角三角形三条边的关系。
学生构图:
问题2:请用a、b、c表示出正方形的面积。
学生:S=c2=a2+b2=2b,其中a=b。
问题3:请同学们再拿出课前准备的四张全等的非等腰直角三角形(直角边用a、b表示,斜边用c表示,其中a≠b),将四个非等腰直角三角形摆放成一个正方形,并观察直角三角形三条边的关系。
学生构图:
问题4:请用a、b、c表示出正方形ABCD的面积。
学生:
SABCD=c2=a2+b2=2ab+(b-a)2>2ab,其中a≠b。
問题5:综上分析请同学们大胆猜想并证明a2+b2与2ab之间的关系。
学生:a2+b2≥2ab,当且仅当a=b等号成立。
问题6:以AB是圆的直径,点C是AB上的一点,设ABa,BC=b过点C作垂直于AB的弦DE,连接AD、BD。
学生构图:
问题7:请根据图形建立a,b和CD的关系。
学生:由三角形相似易得CD2=ab,即CD=,∴a+b≥2,其中C与O重合的时候等号成立(当且仅当a=b时取等号)。
数学学习注重的是逻辑思维的转换,图形语言就是能将抽象思维向形象思维转变的载体,而培养学生动态思维关键就在于培养学生构图能力。案例四的整个基本不等式公式的探究是通过数学三种语言的转化创设问题串引导学生构图,并通过符号语言表示图形隐藏的几何意义,达到概念教学的目的。这样教学不仅让学生掌握了所学知识,更重要的是培养了学生的动态思维,符合培养数学建模的核心素养的要求。
【参考文献】
[1]林青霞.高中生数学概念多元表征的调查研究[D].武汉:华中师范大学,2014.
[2]陆兴华,李兴贵,尧刚,饶永生.互联网+动态数学:网络画板推进数学教学改革[M].长沙:湖南教育出版社,2018.
(基金项目:本文系海南省教育科学规划2021年度课题“基于深度学习的高中数学三种语言转化研究”的研究成果,课题编号:QJH202110070)

