提高水风光可再生能源配网消纳的分布式串联补偿研究

肖军 朱正 鲁晓军 曹阳

摘要：

可再生能源自身存在的波动性及间歇性可能会导致传输线路存在双向潮流、线路过载和电压异常波动等问题，造成部分区域电力供给不足和增大线路传输损耗，进而降低系统运行可靠性。分布式串联补偿器作为一种柔性交流输电设备，可根据上层系统指令对电网进行实时调控。研究了分布式串联补偿器对电网潮流的作用机理，提出了一种可促进可再生能源消纳及抑制电压波动与闪变的分布式串联补偿器电磁暂态建模方法，基于PSCAD/EMTDC构建了含分布式串联补偿器的电磁暂态测试模型。结果表明：分布式串联补偿器可实现对分布式电源能量流向的精准控制和补偿大功率冲击负荷投入时所需的冲击性功率，有效促进分布式可再生能源消纳和抑制电压异常波动。模拟结果验证了电磁暂态模型的正确性与有效性。

关键词：

分布式串联补偿器； 柔性交流输电设备； 可再生能源消纳； 潮流调控； 电磁暂态

中图法分类号：TM 76

文献标志码：A

DOI：10.15974/j.cnki.slsdkb.2023.03.016

文章编号：1006-0081（2023）03-0089-07

0 引 言

配电网在电力系统中起着承上启下的重要支撑作用，随着中国经济的高速发展和“双碳”目标的提出，水电、风电和光伏等分布式电源直接接入配电网成为新趋势［1-3］。分布式能源接入规模越来越庞大，使配电网形态由原本的单向辐射性变为以分布式电源为核心的复杂网络［4-6］，进而导致配电网的运行状态更为多样化，其安全性、灵活性和经济性等方面都面临更大的挑战，具体表现如下。

（1） 可再生能源消纳能力不足。接入配电网的小水电多为径流式，自身调节能力弱，夏季丰水期和冬季枯水期的发电功率相差较大，因此发电受季节波动性影响较大［7］。风电和光伏的出力亦具有较强的随机与波动性。因此，分布式可再生能源并入配电网后，其高效消纳成为难题［8］。配电网可再生能源消纳能力不足，极易导致配电网因局部功率过剩而向上级电网倒送功率的现象，会给整个电网系统的电压质量和继电保护带来严重影响［9-12］。

（2） 电压波动与闪变。风电和光伏出力具有不确定性，其与电网负荷的时空匹配性较差，且电网在风电和光伏并网逆变器设备的影响下会产生大量谐波。而小水電在冬季枯水期会造成配电网末端电压超过下限值，故配电网中大量接入分布式可再生能源后所导致的另一个问题是系统电压的波动与闪变［11］，严重影响了电能质量。在分布式能源接入规模日益庞大的今天，用电负荷呈现出波动性、非线性和非对称性，如何高效地抑制电压波动与闪变是配电网面临的又一严峻挑战。

目前，柔性交流输电系统（Flexible AC Transmission System，FACTS）技术因其优良的可控性和精准的调节能力，已成为分布式可再生能源广泛接入配电网带来诸多问题的高效解决方案［12-14］，而分布式串联补偿器（Distributed Series Compensator，DSC）是其中分散式布置的一个典型代表，其可根据上层系统潮流调控指令进行实时状态感知和潮流调节，是一种适用于现代配电网灵活调控需求的设备［15］。现有文献中，针对DSC的理论研究主要是围绕控制策略及拓扑模型开展。詹雄等［16］研究了DSC的控制保护策略及相应的容量设计方法，并构建了DSC样机系统；饶永杰等［17］研究了DSC的比例谐振控制策略，并以电压补偿为目标提出了对应的控制器参数设计方法。在对DSC的电磁暂态建模方面，Tang等［18］在ADPSS平台构建了DSC的电磁暂态模型，并进行了电压控制与潮流调节的试验仿真，推进了DSC的工程化应用进程；田星等［19］基于RTDS平台完成了DSC主控单元的优化出力分配测试，仿真结果表明所提出的实时优化分配法可以实现最快的子模块响应速度。

本文将从DSC拓扑结构出发，详细分析DSC对线路潮流的作用机理，针对配电网中的可再生能源消纳及电压波动与闪变的问题，构建了含DSC的电磁暂态测试模型，并基于PSCAD/EMTDC仿真平台进行仿真分析，验证了所搭建的电磁暂态模型的有效性与可适性。

1 DSC拓扑结构

DSC分散布置在线路中，由多个子单元组成一个完整的系统，其子单元拓扑结构如图1所示。

DSC子单元由单相电压源型变流器、单匝耦合变压器、滤波电路、电流取能电路、电流采样电路及控制单元组成，其等效电路模型如图2所示。

在图2中，Vdc为直流电容电压，idc为单相变流器直流电流。Vse为单相变流器输出电压，Cdc为直流电容，RL为单相变流器损耗，SA1，SA2，SB1和SB2为每个桥臂上的开关管，Rf为线路等效电阻，Lf为单相变流器的滤波电感，Cf为滤波电容，Vc为滤波电容的电压，i1为变流器输出电流，i2为通过LC滤波电路后DSC交流侧输出电流。

2 DSC数学模型及控制策略研究

2.1 数学模型

由多个DSC子单元串联在一起的数学模型，可将其看作为多个受控源串联在线路上，其等效数学模型如图3所示。

在图3中，V·1，V·2分别是DSC所在线路首端和末端的电压，XL为线路等效阻抗，I·L为线路电流，PL为线路末端有功功率潮流，QL为线路末端无功功率潮流，V·ci为第i个DSC子单元注入到线路的等效电压，i=1，2，…，n。

根据图3的等效模型，可得：

PL=V1V2XL1±∑ni=1VciV21+V22－2V1V2cosθ12（1）

QL=V1V2cosθ12－V22XL1±∑ni=1VciV21+V22－2V1V2cosθ12（2）

式中：V1，V2为DSC所在线路首端和末端电压幅值；θ12为布置有DSC线路的首末端母线电压相位差。可通过控制DSC注入的电压来对线路有功功率PL与无功功率QL进行调控。同时，由于线路运行的功率因数较高，故一般只考虑有功功率潮流的调节效果，因此，DSC运行在潮流调控模式时，通常以有功功率作为其控制目标，无功功率则为随动变量。符号的选择方式为：当DSC工作在容性条件下时取+，感性条件下取-。

根据图2，忽略线路等效电阻Rf，可得DSC的子单元电压和电流特性：

Vse=Vc－Lfdi2dt（3）

i2=i1－CfdVcdt（4）

其中，DSC的注入電压Vc在瞬态表现为输出幅值为Vdc的脉冲波，难以用于构造线性模型，故本文将其平均化，可得：

Vse=mVdcsin（5）

式中：m为调制深度，其取值范围为［0，1］；sin为调制波的单位正弦波。

对式（3）和式（4）进行Park变换，可得：

Vsed=Vcd－LfdI2ddt+ωLfI2qVseq=Vcq－LfdI2qdt－ωLfI2d（6）

I2d=I1d－CfdVcddt+ωCfVcqI2q=I1q－CfdVcqdt－ωCfVcd（7）

式中：ω为工频角频率；d，q下标分别对应相应电气量经Park变换后得到的d，q坐标下的分量；I2q，I2d分别为i2在dq坐标系下的q轴与d轴分量。由于dq坐标系以电流i1相位为参考，因此始终有I1q等于0、I1d等于线路电流的幅值。在不考虑DSC子单元损耗时，可以得到稳态工况下满足：

Vcq/I1d=XcVcd=0（8）

式中：Xc表示DSC子单元端口的等效阻抗。

2.2 控制策略

对单个DSC子单元的控制实质上是对其输出电压的控制，DSC子单元作用到线路的变量为注入电压Vc，对Vc进行Park变换之后，因为其d轴与q轴分量之间存在耦合关系，要实现解耦控制，可使用前馈解耦控制方法，令

CfdVcddt=Kp1V*cd－Vcd+Ki1∫V*cd－VcddtCfdVcqdt=Kp1V*cq－Vcq+Ki1∫V*cq－Vcqdt（9）

式中：V*cd，V*cq为Vcd和Vcq在控制系统中给定的参考值；Kp1和Ki1分别是比例控制参数和积分控制参数。将式（9）转化为s域表达式，可得：

sCfVcd=Kp1+Ki1sV*cd－VcdsCfVcq=Kp1+Ki1sV*cq－Vcq（10）

则DSC子单元注入电压d轴分量Vcd与q轴分量Vcq的闭环传递函数为

Vcd=sKp1+Ki1s2Cf+sKp1+Ki1V*cdVcq=sKp1+Ki1s2Cf+sKp1+Ki1V*cq（11）

由式（11）可知，通过控制Kp1和Ki1的大小，即可改变DSC的动态响应特性。

将式（9）代入式（7），可得：

I2d=I1d－Kp1+Ki1sV*cd－Vcd+ωCfVcqI2q=I1q－Kp1+Ki1sV*cq－Vcq－ωCfVcd（12）

上式可作为外环控制特性，所得到的I2d和I2q可作为内环控制环节的电流跟踪指令I2d*和I2q*。

与式（10）类似，得到电流I2d和I2q的控制特性：

sLfI2d=Kp2+Ki2sI*2d－I2dsLfI2q=Kp2+Ki2sI*2q－I2q（13）

将式（13）代入式（6），可得：

Vsed=Vcd－Kp2+Ki2sI*2d－I2d+ωLfI2qVseq=Vcq－Kp2+Ki2sI*2q－I2q－ωLfI2d（14）

式（12）和式（14）共同构成了DSC子单元交流侧的控制系统原理，输出电压d轴与q轴分量。根据上层潮流调控指令可确定DSC对线路的注入电压的大小，进而可以快速、准确地调节线路潮流。

当输入有功功率潮流指令PLref时，可以反推得到DSC的所有子单元串联后所需要补偿的阻抗值Xcsum的计算式：

Xcsum=V1V2sinθ12PLref－XL（15）

线路电流的有效值为

IL=（V1－V2cosθ12）2+（V2sinθ12）2XL+Xcsum（16）

3 电磁暂态建模与仿真

3.1 电磁暂态建模

本节采用如图4所示仿真系统验证DSC对可再生能源消纳的促进能力和对电压波动的能力。在PSCAD/EMTDC仿真平台中完成了仿真测试系统的电磁暂态模型构建，其中，可变负荷Gs可产生大功率冲击来模拟系统中的电压波动来源，在测试电压波动时才投入使用。

在图4中，配电网仿真系统的基准电压为380 V，母线I与母线II分别连接一个三相交流电压源模拟无穷大电网，两个电源的相角差为11.431°，母线I处可变负荷Gs为0.036 MW。在母线III处装有一个容量为0.071 MW的恒功率负荷，并用一个三相电源模拟可再生能源电源接入系统，其额定功率为0.113 MW。DSC装置安装在线路I上。

所构建含DSC及线路等效阻抗参数的简单电力系统的仿真模型如图5所示。所搭建的DSC子单元一次系统详细电磁暂态仿真模型如图6所示，控制系统模型如图 7所示。其中，设置DSC子单元的交流侧滤波电容为500 μF，滤波电感为0.2 mH。

3.2 仿真分析

3.2.1 促进可再生能源消纳仿真分析

在图4中，母线III处用一个三相电源模拟一个可再生能源电源接入系统，其额定功率为0.113 MW。同时设定母线III处的负载额定功率是0.071 MW，故线路III满载，且可再生能源发电有盈余。现测试DSC装置能否将可再生能源的多余发电量通过“线路II—母线I—线路I”的路线输送至母线II处的受端电网以促进消纳。

对上述应用场景进行仿真验证。在1 s时，将DSC投入线路中；1.5 s时开始对直流电容充电；2.1 s时开始投入变流器潮流调节控制器对每相的潮流进行调整；3.5 s时开始投入可再生能源电源。DSC单相电容电压如图8所示。

可以看到，在1.5 s时，DSC对变流器的直流电容进行充电，电容电压在0.2s后达到给定值0.25 kV，在2.1 s时的波动是由于潮流调节控制器投入所导致的，之后也一直稳定在0.25 kV。

母线II处每相有功功率潮流如图9所示。1 s之前未投入DSC，线路原始有功功率为0.028 MW；在1 s时投入DSC后，由于装置内的变压器增加了线路阻抗，故有功功率略有下降，大小不足1%；在1.5 s时对直流电容进行充电，使线路有功功率出现了短时下降，但很快就恢复到原值；在2.1 s时投入潮流调节模式后，有功功率达到给定值0.030 MW；在3.5 s时投入可再生能源，并设定线路I传输的有功功率给定值为0.044 MW，功率快速上升到稳定值。

母线II处每相无功功率潮流如图10所示。在1 s时将DSC投入线路后，容性无功功率略有减少；在2.1 s及3.5 s给定潮流控制后，无功功率均能实现稳定。

从图9和图10可以看出：

（1） 在可再生能源电源投入后，通過线路I传输的有功功率潮流由0.030 MW/相增大为0.044 MW/相，有功功率变化量为0.014 MW/相。

（2） 可再生能源发出的0.113 MW功率除了一部分用于0.071 MW负荷供电外，剩下的0.014 MW/相的功率将会传递到系统中，恰好等于线路I传输的有功功率变化量。

（3） 上述结果表明，可再生能源发出的多余电能全部通过“线路II—母线I—线路I”的路线输送至母线II处的受端电网消纳，验证了DSC可按照预期改变线路潮流，实现对分布式电源能量流向的精准控制，有效促进了分布式可再生能源消纳。

3.2.2 解决电压波动和闪变仿真分析

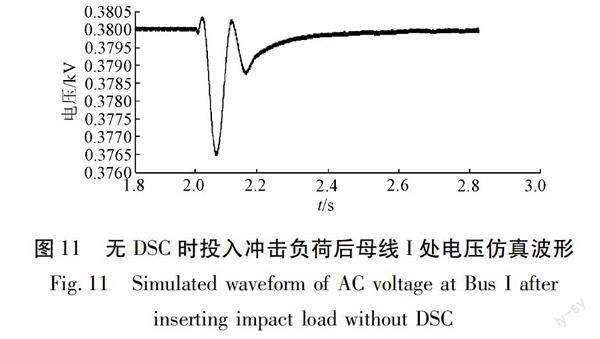
如图11所示，在线路不投入DSC的情况下，在2 s时投入大功率冲击负荷，母线I处的电压产生剧烈波动和闪变，母线电压跌落至376.5 V，最大电压变化率约为100 V/s，电压恢复时间较长，超过了0.8 s。

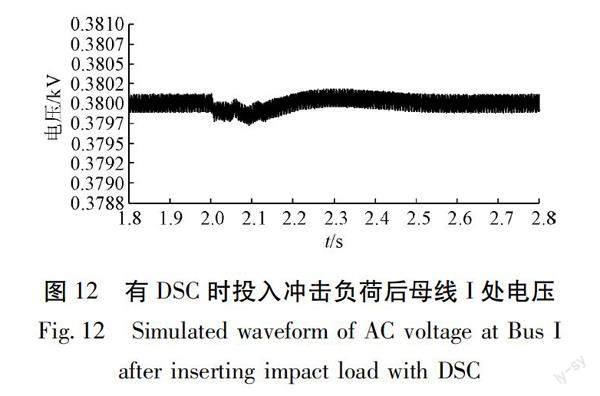
投入DSC后，同样在2 s时投入大功率冲击负荷。如图12所示，DSC可把母线I的电压波动维持在±0.3 V之间，在2.5 s后重新稳定于380 V。与图12相比可知，DSC可有效抑制因冲击负荷导致的电压波动与闪变。

DSC与冲击负荷的无功功率波形如图13所示。其中，Q1为冲击负荷吸收的无功功率，Qsh为DSC变流器吸收的无功功率。可以看到，在2.0～2.2 s间，冲击负荷与DSC变流器吸收的无功功率呈大小相等、符号相反的互补变化趋势，说明变流器可以有效地向冲击负荷提供无功功率，从而减弱冲击负荷对系统无功功率造成的影响。同时，因为变流器还需要消耗无功功率以维持母线电压恒定，所以吸收的无功功率稳态值不为零。

DSC与冲击负荷的有功功率波形如图14所示。其中，P1为冲击负荷的有功功率，Psh为DSC变流器的有功功率。可以看到，在2.0～2.2 s间，冲击负荷与DSC变流器的有功功率呈相反的互补变化趋势，说明变流器可以有效地向冲击负荷提供有功功率，从而减弱冲击负荷对系统有功功率造成的影响。最终冲击负荷维持于0.036 MW，达到额定工作状态。

4 结 论

本文首先对分布式串联补偿器（DSC）的拓扑结构进行了分析，阐明了DSC对线路潮流的作用机理，提出了一种能促进可再生能源在配电网消纳和抑制配电网电压波动与闪变的DSC电磁暂态建模方法，然后构建了含DSC的简单测试系统，基于PSCAD平台对所构建的电磁暂态模型进行了仿真验证，结果表明：

（1） 本文所构建的DSC电磁暂态模型能实现对输入电压指令的灵敏跟踪，通过改变自身输出阻抗的性质（感性/容性）来改变注入线路的等效阻抗；

（2） DSC可根据上层潮流调控指令强制控制线路潮流走向，在系统安全运行范围内实现对分布式可再生能源能量流向的精准控制，从而可有效解决配电网中分布式可再生能源消纳问题；

（3） DSC能够补偿大功率冲击负荷投入时所需的冲击性功率，同时还可以根据负荷的波动特性来补偿波动性功率，从而实现对配电网中节点电压波动与闪变的抑制。

参考文献：

［1］ 尹昌洁，权楠，苏凯，等.我国分布式能源发展现状及展望［J］.分布式能源，2022，7（2）：1-7.

［2］ 孙舒婷.含分布式能源接入的配电网优化调度研究［J］.自动化与仪器仪表，2022（2）：43-47.

［3］ 李海明，姜超，闫宇，等.分布式新能源大规模接入对配电网影响及应对［J］.农村电工，2022，30（2）：28-29.

［4］ 余涛，冯斌，韦冬妮，等.含分布式能源的主动配电网“源-网-荷-储”协调经济调度［J］.水利水电技术（中英文），2021，52（6）：215-222.

［5］ 闫群民，王佳，沈延峰，等.含小水电的配电网电压无功优化控制综述［J］.电力电容器与无功补偿，2022，43（1）：1-11.

［6］ 施烨.分布式电源接入对配电网电能质量的影响及应对策略研究［D］.南京：东南大学，2016.

［7］ 李劲，唐捷，张勇军，等.小水电群对配电网无功电压影响机理分析［J］.南方电网技术，2012，6（5）：39-42.

［8］ 姜云鹏，任洲洋，李秋燕，等.考虑多灵活性资源协调调度的配电网新能源消纳策略［J］.电工技术学报，2022，37（7）：1820-1835.

［9］ 汤项雷.含小水电分布式电源的配网线路串联补偿优化［J］.电工材料，2021（2）：38-40.

［10］ 张锡填，张勇军.10kV并联电抗器在含小水电配电网中的优化方法［J］.水电能源科学，2013，31（10）：217-220.

［11］ 吕风仪，曾次玲，叶文浩，等.含分布式电源并网的配电网电压波动特性分析［J］.电气自动化，2021，43（1）：81-84.

［12］ 曹红，姜萌，陈俊，等.风电与柔性交流输电系统优化选址对配电网电压稳定的影响分析［J］.电力与能源，2021，42（5）：573-576，585.

［13］ 刘颍琪.微电网分布式潮流控制器控制策略的研究［D］.天津：河北工业大学，2019.

［14］ 宋鹏程.含统一潮流控制器电力系统的控制与优化相关问题研究［D］.杭州：浙江大学，2018.

［15］ 舒欣.分布式静止同步串联补偿器协调控制策略研究［D］.武汉：武汉理工大学，2019.

［16］ 詹雄，王宇红，赵刚，等.分布式静止同步串联补偿器研究与设计［J］.电力电子技术，2019，53（3）：95-98.

［17］ 饶永杰，陈亮亮，高树功，等.分布式同步串联补偿器的比例谐振控制策略研究［J］.电力电容器与无功补偿，2018，39（6）：138-144.

［18］ TANG A H，LU Z J，YANG H Y，et al.Digital/analog simulation platform for distributed power flow controller based on ADPSS and dSPACE［J］.CSEE Journal of Power and Energy Systems，2021（1）：181-189.

［19］ 田星，馮雪，党东升，等.分布式静止串联补偿器潮流控制优化分配分析［J］.电子测量技术，2020，43（4）：53-57.

（编辑：李 慧）

Distributed series compensators for enhancing renewable energy consumption in distribution grid containing hydro-wind-solar power

XIAO Jun，ZHU Zheng，LU Xiaojun，CAO Yang

（Changjiang Survey，Planning，Design and Research Co.，Ltd.，Wuhan 430010，China）Abstract：

The embedded fluctuation and intermittency of renewable energy may lead to several problems of the transmission lines，including bi-directional power flow，overload current and abnormal voltage variation，which results in deficiency of power supply and increase of transmission loss.Finally，the system reliability is reduced.The distributed series compensator （DSC），one of the flexible AC transmission （FACT） equipment，is able to conduct real-time regulation of the power network according to upper-level system orders.The control mechanism of the DSC towards power system flow was studied based on its topology and structure.The electromagnetic transient modeling method of the DSC for promoting renewable energy consumption and depressing voltage variation was researched.The test model of DSC based on PSCAD/EMTDC platform was built.The results showed that distributed series compensator can realize the precise control of the energy flow direction of the distributed power supply and compensate the impact power required when the high-power impact load was put into operation，which can effectively promote the consumption of distributed renewable energy and suppress the abnormal voltage fluctuation with its correctness and validity verified by simulation results.

Key words：

distributed series compensator；flexible AC transmission equipment；renewable energy consumption；power flow regulation；electromagnetic transient modeling

收稿日期：

2022-09-29

基金项目：

长江勘测规划设计研究有限责任公司自主创新项目（CX2018Z34）

作者简介：

肖 军，男，高级工程师，硕士，主要从事输变电电气一次设计工作。E-mail：xiaojun@cjwjsy.com.cn

通信作者：

鲁晓军，男，高级工程师，博士，主要从事新能源及柔性直流研究。E-mail：luxiaojun1212@foxmail.com