考虑隐私信息共享水平的定向广告投放与产品定价研究
何 向, 李 莉, 张 华, 朱星圳, 杨文胜
(南京理工大学 经济管理学院,江苏 南京 210094)
0 引言
定向广告是指商家借助网络与信息技术收集大量消费者信息,并利用这些信息将市场划分为不同细分市场,同时针对每个细分市场施以不同广告策略的一种模式[1]。随着商家获得越来越多的消费者信息,消费者开始逐渐意识到他们的在线行为正在受到监控,个人隐私信息正在被收集并可能被共享。随着人们对隐私的关注日益加深,一些消费者采取了积极的措施来保护隐私信息并阻止商家对其进行个性化推荐的尝试[2]。例如,当移动App试图获取来自消费者的相册、通讯录以及地理位置等敏感数据时,一些消费者明确表示“拒绝”或仅同意提交部分信息。
消费者可以主动管理隐私信息共享水平高低的行为,使得商家的广告投放和产品定价策略变得更加复杂。已有大量研究关注了商家如何利用消费者隐私信息来调整广告策略这一主题,这些研究大致可分为三类。第一类是基于消费者对购买渠道的偏好来调整其定向广告策略[3],从而提高渠道整体利润,在这类研究中商家通常会根据所获得的消费者渠道偏好信息将其交易渠道进行分类,并根据对渠道偏好大小的变化来调整其广告投放策略。第二类研究是基于消费者对产品的品牌偏好来调整商家的价格策略[4,5],这类研究大多以商家生产具有横向差异化的同质产品为主,基于商家所获取消费者的品牌偏好信息来调整价格策略。第三类是基于商家定向广告投放的目标群体范围调整其价格策略与广告策略[6~8],这类研究中商家可以调整定向广告投放的精准度[6],并考虑投放精准度对企业利润的影响。以上研究均立足于商家如何针对已获取的消费者隐私信息而进一步调整广告投放策略,对于商家而言,消费者属于被动提供信息的一方,无法参与隐私管理来调整隐私信息共享水平的高低。鲜有研究讨论当消费者可以主动管理隐私信息共享水平时,商家的广告投放与产品定价策略将会发生何种变化。
故本文的创新性在于,我们考虑当消费者可以主动管理其隐私信息共享水平的高低时,商家的最优广告投放与产品定价策略,同时商家又该如何调整其广告投放与产品定价策略来应对消费者隐私信息共享水平的变化。对此,拟研究以下几个问题:(1)与未共享隐私信息相比,商家是否会受益于消费者所共享的隐私信息?(2)如果市场上存在若干商家,消费者的隐私信息共享水平会如何影响商家的收益?(3)为达到最大收益,商家的产品定价应该如何随着隐私信息共享水平的变化而调整?
1 模型
1.1 市场环境
我们考虑某线上平台中有n位商家,按照图1所示沿着顺时针方向对称分布于Salop圆形城市中。与传统Hotelling模型中存在两个生产同质产品的商家不同,Salop圆形城市模型中允许存在n≥3位商家,这一模型适用于描述存在多个商家共同竞争时的市场环境,与文献9、10中的研究一致,也与现实更为贴切,同时该模型还能考虑到商家的数量对广告策略的影响。规模为1的消费者均匀分布在商家之间,这一假设与CHEN等学者的研究假设保持一致[11]。平台中存在一位主导商家i(Dominate seller)与n-1位非主导商家(Non-dominate seller),其中主导商家的单位产品质量vi与单位产品定价pi均高于市场中的其他商家。为了不失一般性,除了主导商家外,其余商家均生产同质产品,单位产品定价大小满足对称相等且依次递减,即pi+1=pi-1,pi+2=pi-2,…,pi+(n-1)/2=pi-(n-1)/2,且pi>pi+1>…>pi(n-1)/2。同时,为了确保市场中只有一位主导商家,以及剩下的n-1位非主导商家满足产品质量两两对称相等的条件,模型中假设平台中的商家数量n为奇数。假设图1中的单位圆周长为1,则沿圆的任何两个相邻商家之间的最短距离为1/n(在没有特意指出时,下文中所提及的距离均表示为两个主体之间的最短距离)。n位商家在特定情况下对消费者投放信息性广告,信息信广告旨在传递产品功能与价格等信息,而不以改变消费者偏好为目的,商家则需要对产品定价的高低做出决策。同时,平台中的商家需要通过竞价的方式来获得平台中所提供的k个广告位(k 图1 圆形Salop城市 我们假设市场中的商家都以二价竞拍(Second-price auction)的规则竞争k个广告位[12],这一假设可以避免商家之间的恶性竞价,且与实际Google、Microsoft Bing以及Yahoo!等平台线上竞价策略相符[13]。竞价结束后,竞价成功的商家会获得相应的广告位,并按照一定的方式投放给消费者。商家投放广告的方式与商家是否利用消费者所共享的隐私信息有关。具体而言,若商家不利用消费者所共享的隐私信息,则商家向所有消费者均投放大众广告(Mass advertising);若商家决定利用消费者所共享的隐私信息,则商家可以大致确定圆圈中每个消费者的位置,即消费者对商家的偏好,商家根据消费者的偏好向消费者投放相应的定向广告(Targeted advertising)。 消费者在进入某平台购物之前,需要与该平台签订服务协议来参与隐私管理。协议中包含了消费者向该平台中的商家所愿意共享的隐私信息水平,例如,允许平台获取其通讯录信息、相册内容、cookie信息等等,允许被获取的信息越多,消费者的隐私信息共享水平y越高。为了便于计算,我们假设y代表该购物平台中整体消费者的隐私信息共享水平均值,y在(0,1)内服从均匀分布,这一假设是由于当商家在制定某平台的广告投放策略时,需要掌握该平台中消费者的整体隐私共享水平,而非具体某位消费者的隐私信息共享水平。当消费者确定好y的大小之后,平台将隐私信息共享给平台中的所有商家。 随后,商家根据消费者所共享的隐私信息来判断其对商家的偏好水平,并对消费者投放相应的信息性广告。偏好水平越高,则消费者对该商家所提供的产品或服务的购买倾向性越高,反之越低。在图1中,消费者与商家之间的距离揭示了消费者对商家的偏好水平,距离越长,消费者对商家的偏好水平越低。故对于图1中的商家而言,偏好水平最高的消费者是与商家位于同一位置的消费者。 当消费者在购物平台中收到来自商家的信息性广告时,将根据其产品或服务的效用大小来决定是否购买商家所提供的商品或服务。例如图1所示,任意消费者j在区间|i,i+1|与|i,i-1|内都可以收到来自主导商家i的促销广告,记j+为区间|i,i+1|内的消费者,j-为区间|i,i-1|内的消费者,则j+可同时收到商家i与i+1的信息性广告,j-可同时收到商家i与i-1的信息性广告。在本文中,消费者在购买某产品或服务所获得的效用不仅与消费者对商家的偏好有关,还与商家对消费者所投放的广告类型有关。 (1)大众广告 由于商家向整个市场投放大众广告,则根据模型中需求的对称性,大众广告下主导商家的需求为: (2)定向广告 若商家利用消费者所共享的隐私信息,则向消费者投放定向广告(后文中均用上标T表示)。当商家i对市场中的所有消费者均投放定向广告时,消费者j对任意一位商家i的效用为 根据模型假设,可进一步计算出当商家利用或不利用消费者所共享的隐私信息时,主导商家的最优均衡策略。 命题1在广告竞价中,当商家遵循二价规则参与竞争广告位时,商家的广告出价实际由产品定价决定,即bi=pi为商家的占优策略。 命题2若市场中除了主导商家外,其他商家生产同质的产品,则均衡状态下,主导商家与其他商家分别投放大众广告与定向广告的最优均衡策略如表1与表2所示。 表1 商家投放大众广告时的最优均衡策略 表2 商家投放定向广告时的最优均衡策略 命题3消费者所共享的隐私信息是否会给商家带来收益会受到平台中商家数量n的影响,具体而言:(a)当n小于一定数量时,商家不利用消费者所共享的隐私信息(即商家投放大众广告)时所获得的收益高于商家利用隐私信息(即商家投放定向广告)时所获得的收益;(b)当n大于一定数量时,商家利用消费者所共享的隐私信息时所获得的收益高于商家不利用隐私信息时所获得的收益。 接下来,我们主要考虑当商家数量较多且商家选择利用消费者所共享的隐私信息(即投放定向广告)这一情境,旨在研究在定向广告下,消费者的隐私共享水平如何影响商家的收益,以及为达到最大收益,商家的产品定价策略应该如何随着隐私共享水平的变化而调整等问题。 命题5消费者向商家共享隐私信息水平的变化对主导商家的收益会产生影响且该影响与其产品价值有关:当产品价值较高时,收益随着隐私信息共享水平的增长而增长;当产品价值较低时,收益随着隐私信息共享水平的增长而降低。 在Salop模型中,每位商家都拥有两位相邻商家,由命题5可知,商家与其相邻商家的产品价值差异调节了隐私信息共享水平对商家收益变化的影响。对于主导商家i而言,当其产品价值较低(接近相邻商家)时,消费者所共享的隐私信息将使主导商家的收益变小;当主导商家的价值较高(高于相邻商家)时,消费者所共享的隐私信息将使主导商家的收益变大。命题5的结论启发了我们,除了隐私信息水平以外,相邻商家价值的变化是否会对商家的需求与收益产生影响,我们将在第3部分讨论这一问题。 在基础模型中,本文强假设了市场中除了一位主导商家i以外,其余商家的产品价值均相等的情景。接下来,我们将放宽此假设并考虑一种特殊情况,即对于主导商家i而言,其左右对称的两个相邻商家具有相同的产品价值,且产品价值与价格随着与距离的增加而递减(即vi+1=vi-1,vi+2=vi-2,…,vi+(n-1)/2=vi-(n-1)/2且vi+1>vi+2>…>vi+(n-1)/2,pi+1=pi-1,pi+2=pi-2,…,pi(n-1)/2=pi-(n-1)/2,且pi>pi+1>…>pi+(n-1)/2),这一假设与现实情况相符。例如在智能手机市场中,存在“苹果”作为价值和价格最高的“主导商家”,以及价格和价值相近但略低于主导商家的“小米”和“华为”作为“其他商家”。我们将用该情况来说明,消费者的隐私信息共享水平如何影响平台中不同商家的需求与收益,同时分析相邻商家的产品价值变化将如何影响平台中不同商家(包括主导商家与其他商家)的收益。 根据竞价规则,商家i+(n-1)/2的广告成本为商家i+(n+1)/2的出价,则商家i+(n-1)/2的总收益为: 根据公式(6)与公式(7),可以得出如下命题: 命题6若市场中除了主导商家外,其他商家生产不同质的产品,则均衡状态下主导商家i与其他商家i±(n-1)/2投放定向广告时的最优产品定价、最优需求与最优收益如表3所示。 表3 定向广告下主导商家与其他商家的均衡策略 命题7当产品价值处于不同的取值范围下,消费者的隐私信息共享水平对其他商家的最优产品定价会产生不同的影响:当产品价值较小且隐私信息共享水平较高时,最优产品定价随着隐私信息共享水平的提高而上升;当产品价值逐渐增加到一定阈值且隐私信息共享水平较高时,最优产品定价随着隐私信息共享水平的提高而下降。 为了更加直观的体现命题7与命题4之间的对比,本文通过数值算例来刻画主导商家与其他商家的产品定价策略。由数值算例可知,当消费者的隐私信息共享处于中间水平时,产品的最优定价最高,同时也伴随着主导商家的收益达到最大值。当消费者的隐私信息共享水平超过一定阈值后,产品定价与最优收益均开始递减。对于其他商家而言,产品最优定价策略则变得更加复杂。具体而言,产品最优定价最高点位于产品价值最大,隐私信息共享处于中间水平时。因此,与主导商家不同的是,消费者隐私信息共享水平对其他商家产品最优定价策略的影响,还受到其自身产品价值区间的调节。 命题8消费者向商家所共享隐私信息水平的变化对不同商家的需求会产生不同程度的影响:(a)对于主导商家i而言,隐私信息共享水平越高,需求越大;(b)对于其他商家(例如i+1)而言,当其产品价值足够大时,消费者的隐私信息共享水平越高,商家的需求越大;当其产品价值较小时,消费者的隐私信息共享水平越大,商家的需求越小。 命题9相邻商家价值的变化对不同商家的需求与收益都会产生不同程度的影响:(a)不论是主导商家还是其他商家而言, 当相邻商家的产品价值增长时,产品需求均呈下降趋势;(b)对主导商家而言,当相邻商家的产品价值增长时,收益呈下降趋势;(c)对其他商家而言,若相邻商家的产品价值足够大,收益随着相邻商家的产品价值的增长而增长;若相邻商家的产品价值足够小,收益随着相邻商家的产品价值的增长而减小。 本文针对消费者参与隐私管理下的定向广告投放与产品定价问题,构造了一个圆形城市模型,在该模型中,商家进行网络广告投放并对产品定价展开决策,且消费者可以主动管理其隐私信息共享水平。我们发现,定向广告在某些情境下不一定是最适合线上商家的广告投放形式,若市场中商家数量较少,商家依旧可以选择投放大众广告。同时,商家并非在任何时候都会获益于消费者所提供的隐私信息,故商家在决定是否利用消费者的隐私信息时还应考虑市场中的商家数量。 其次,消费者隐私信息共享水平的高低会影响商家的产品定价策略。在过去的研究中,消费者的隐私信息可以使公司获益,因为商家会根据隐私信息来识别偏好水平较高的消费者并进行价格歧视。在本文研究中,当消费者积极共享隐私信息时,上述结果可能发生变化,虽然隐私信息可以使商家在一定程度上受益,但消费者共享的隐私信息超过某一阈值后,商家会降低产品的定价水平。
1.2 广告竞价与投放
1.3 消费者的隐私管理
1.4 消费者效用

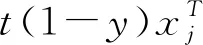

2 除主导商家外,其他商家生产同质产品






3 除主导商家外,其他商家生产不同质产品


4 结论

