两阶段分析框架下加性交叉效率的测度与分解
薛君梅, 王应明
(福州大学 经济与管理学院,福建 福州 350108)
0 引言
数据包络分析(Data Envelopment Analysis, DEA)是在1978年由CHARNES和COOPER等[1]提出的效率评价方法。传统DEA模型普遍存在两个问题:一是“黑箱”评价无法探知内部过程对效率的影响;二是没有考虑到其他决策单元(Decision-Making Unit, DMU)的影响,易出现以偏概全的现象。
为了挖掘系统内部的影响,CHARNES和COOPER等[2]首次提出了网络DEA。SEIFORD和ZHU[3]用两阶段过程对美国商业银行的绩效进行了研究,但没有考虑两阶段间的联系。有学者对其进行了改进和延展:KAO和HWANG[4]把传统DEA修改为整体过程效率等于两个子过程效率的乘积,但这仅适用于规模收益不变的情况;CHEN等[5]进一步考虑到规模收益可变和不变的情况,开发了加性效率分解法,这比KAO和HWANG[4]的方法适用性更强;WANG和CHIN[6]发现两阶段过程的整体效率也可用加权调和平均值表示,同时对KAO[4]和CHEN[5]的模型加以拓展。
交叉效率评价是解决第二个问题的有效手段,考虑了所有决策单元在效率评价的作用。DOYLE和GREEN[7]为解决不唯一性问题,提出了仁慈型和激进型模型。WANG和CHIN[8]从决策单元更关注自身而非其他的角度提出了中性交叉效率模型,并构建新参照点[9]。
尽管如此,交叉效率方法并没有考虑到系统内部的因素,因此有部分学者结合网络DEA进行研究:苏航[10]、ORKCU等[11]和王美强等[12]都以中性交叉效率评价为基础进行研究,提出了新的两阶段交叉效率模型,但对其他决策单元的关注较少;MA等[13]从非合作博弈的角度构建了两阶段博弈交叉效率模型;KAO和LIU[14]基于KAO和HWANG[4]的研究进行扩展,提出了两阶段乘积交叉效率模型。然而,上述研究都没有考虑到决策者主观偏好的影响。
通过文献回顾可以发现,学者们为完善数据包络分析做出了许多努力,但将交叉效率和网络DEA相结合的研究还处于起步阶段。本文借鉴CHEN等[5]的加性效率分解思想,考虑决策者偏好,通过设定不同过程的优先级构建两阶段加性交叉效率模型,分为三种情况:整体优先、阶段一优先和阶段二优先,在计算整体效率时根据加性效率分解思想考虑两阶段权重在j=d和j≠d的不同取值,并结合例子验证所提出模型的合理性和有效性。
1 基本理论与方法
1.1 DEA交叉效率
假设共有n个DMUs,每个DMUj都用xj=(x1j,…,xmj)表示投入矩阵,用yj=(y1j,…,ysj)表示产出矩阵,最初由CHARNES等人提出了CCR模型去测量DMUd的效率,即模型(1)。
模型(1)中的投入和产出分别对应权重vid=(v1d,…,vmd)和urd=(u1d,…,usd),可得DMUd的最优权重,代入模型(2)表示DMUj的互评效率是用DMUd的乘子计算得到。
为解决模型(1)的最优解不唯一问题,DOYLE和GREEN引入了辅助目标优化模型,分别为仁慈型(模型(3))和激进型模型。
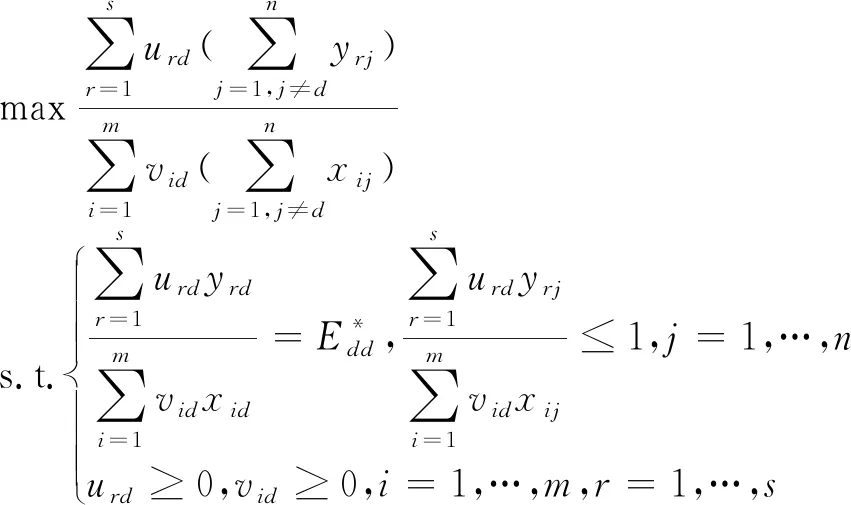
仁慈型模型在保证自身效率最高的前提下,尽可能地最大化其他决策单元的效率,因此目标函数为求最大值;而激进型模型则是求最小值,其他约束不变。
1.2 两阶段DEA
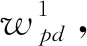
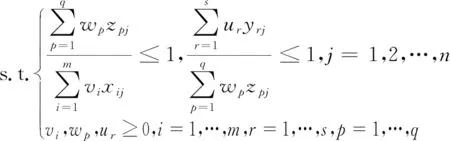
(4)
分别表示阶段一和阶段二的投入占总投入的比重,代入模型(4)后转化为:
(5)
2 两阶段加性交叉效率模型
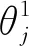
在“互评”体系中j≠d,即等式(7)。
(7)
2.1 整体优先模型
在自评体系中,整体效率的目标函数为
代入等式(6):
在保证系统自评效率最优的前提下求解DMUj的互评效率:
这里不能直接使用Charnes-Cooper转换转化为线性规划来求解。比如令
有
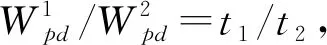
但模型(10)为非线性规划,代入等式(7)后目标函数为
此时用Charnes-Cooper转换化为线性规划模型(11)。
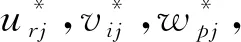
2.2 阶段一优先模型
阶段一优先模型的线性规划如(12)和(13)所示。
(12)
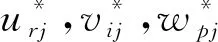
进一步可得整体效率为
2.3 阶段二优先模型
与阶段一优先模型同理,阶段二模型自评和互评效率目标函数为
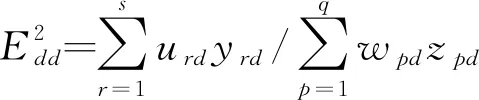
其他不变。
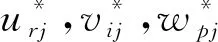
整体效率为
需要注意的是,每种模型都是采用对DMU自身最有利的权重进行计算,而这不一定对其他过程最优,故可能在交叉效率矩阵中出现互评效率大于自评效率的情况。
DMUj的整体、阶段一和阶段二的最终交叉效率均用算术平均值表示:
3 算例分析与实证
例1选取参考文献4中的24家台湾非人寿保险公司作为研究对象。KAO提出了两阶段效率分解结构,阶段一是保险的营销过程,以营业费用和保险费用作为投入,产出为直接书面保费和再保险保费,同时是阶段二的投入;阶段二是保险公司的投资过程,产出为承保利润和投资利润。本文沿用KAO的计算顺序,用阶段二优先模型进行效率评价。
如表1所示,第二栏是CHEN等[5]运用两阶段加性效率模型的结果,第三栏是运用阶段二优先模型得到的结果,每一栏从左到右分别代表整体效率、阶段一和阶段二的最终效率。对比各部分效率可知,所有保险公司都没有达到有效水平,这是因为交叉评价具有更强的辨别力,一家公司的效率不是仅由其自身评价得到的,而是由所有公司共同评价得到。在投资过程中,第7、8、9、10、13、14、17、20和24家公司的交叉效率大于自评效率,这是因为CHEN模型中子阶段的自评效率是在保证整体效率和当前阶段效率最优的前提下计算得到的,而本文中子阶段的效率仅保证自评效率最优,故可能出现本文模型交叉效率值大于CHEN模型自评效率值的情况。将对应阶段的效率相比后发现二者数值波动趋势相似,说明本文模型具有合理性。
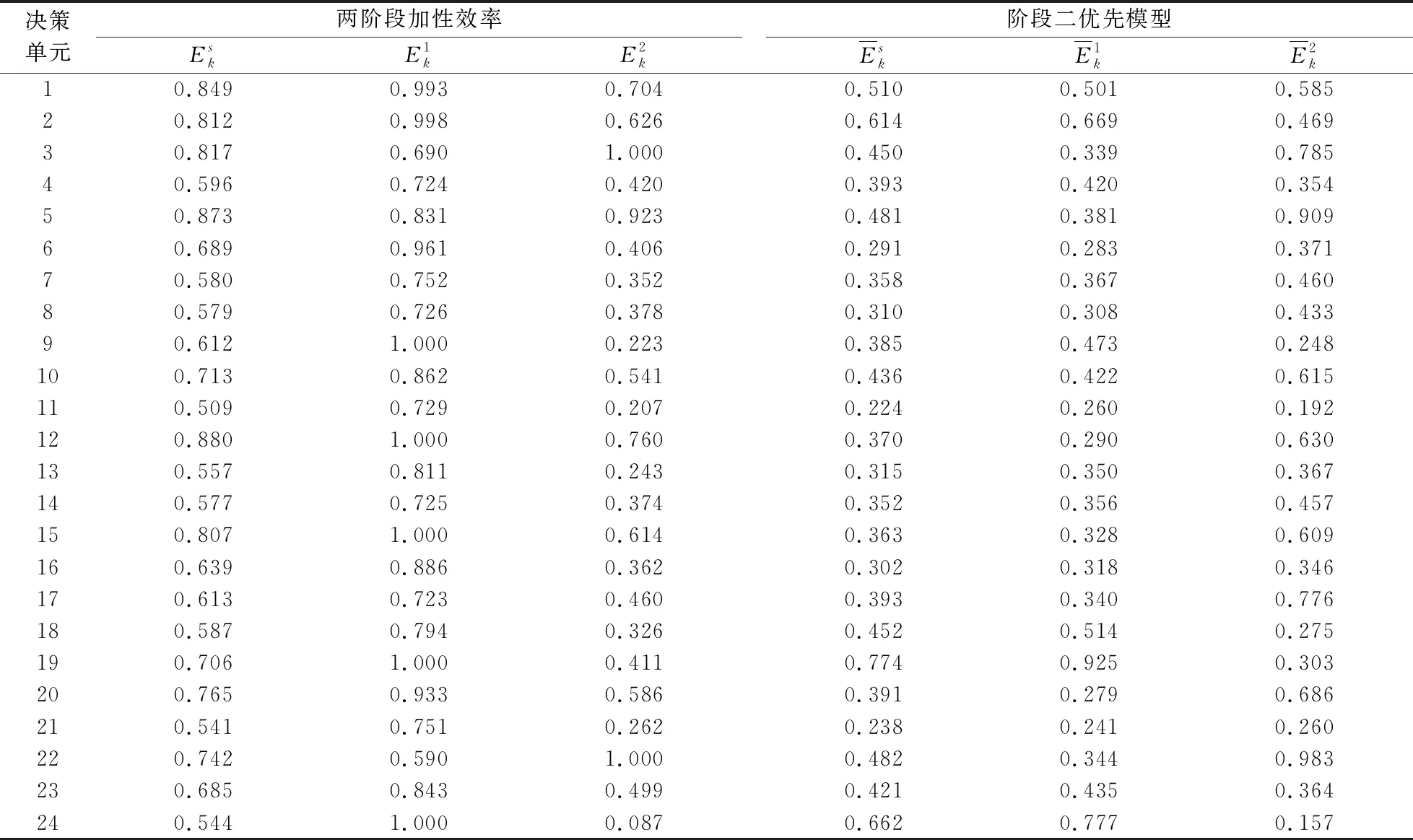
表1 两阶段加性效率对比
例2选取参考文献15的部分数据,将某国有商业银行的10家二级分行作为研究对象。商业银行的业务运作过程是典型的两阶段结构,阶段一是吸储过程,以固定资产净值和员工人数作为投入,产出为存款,同时是阶段二的投入;阶段二是盈利过程,产出为账面利润。这里采用阶段一优先模型对商业银行的运作效率进行测算,并以第10家分行为例说明两阶段加性交叉效率的分解结果。
如表2所示,第二栏是阶段一优先模型的计算结果,从左到右表示整体效率、阶段一和阶段二的效率;第三栏表示第10家分行的交叉效率及分解结果,从左到右分别表示DMU10阶段一和阶段二的权重、整体交叉效率、阶段一和阶段二的交叉效率。
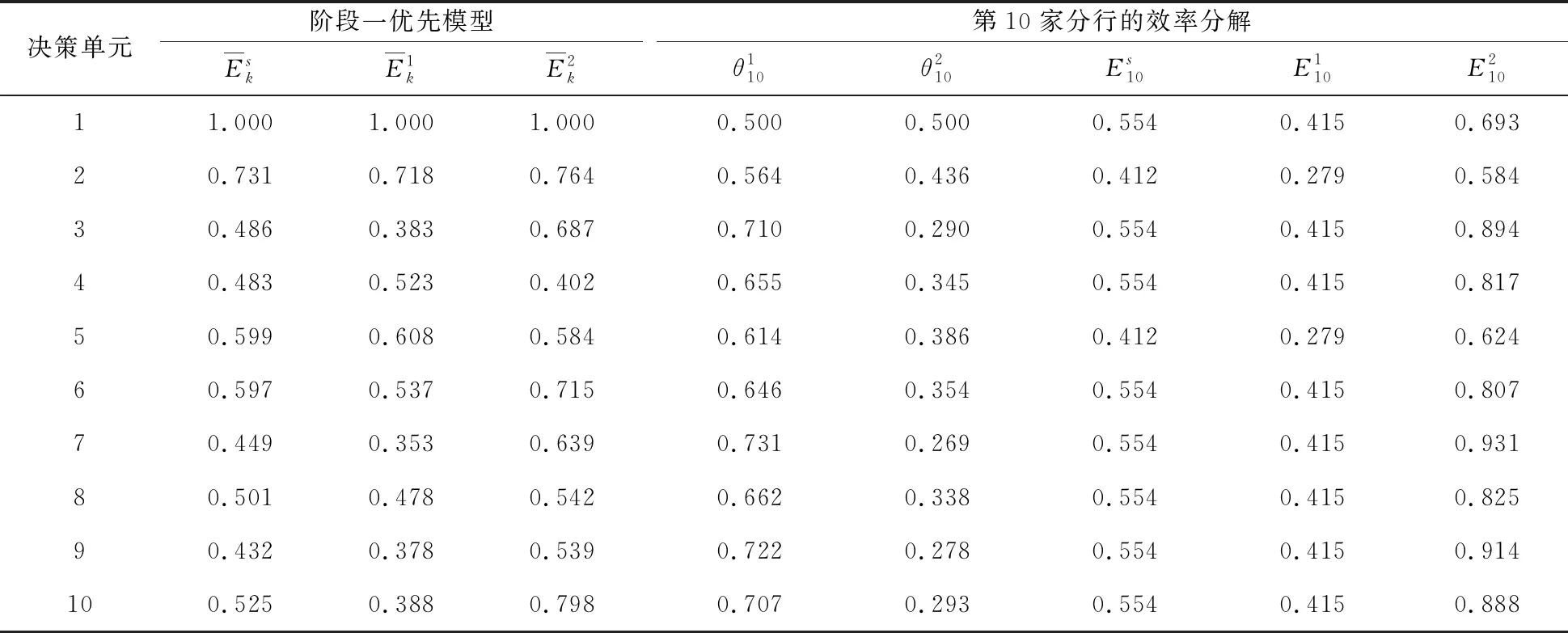
表2 第10家分行的两阶段交叉效率分解结果
在阶段一优先时,第1家分行的整体和子阶段都是有效的,其他分行均为无效。从第10家分行的阶段一权重均不小于0.5,验证了阶段一优先模型的可行性,此时整体效率的高低主要取决于阶段一的效率水平,整体效率是子阶段效率的加权平均值。
例3选用参考文献16的部分数据,将供应链上的买卖过程分为两阶段,阶段一为卖出,阶段二为买入。买卖过程对供应链运作都至关重要,决策者追求整体效益最佳,故采用整体优先模型对供应链的运营效率进行测算。
如表3所示,从左到右分别表示整体、阶段一和阶段二的最终效率和排序。可以发现整体效率低下主要是由卖出过程的效率不高导致的,当卖出的效率较高时,整体效率也会有较大幅度的提升(如DMU10)。整体的效率和排序一般位于子阶段的效率和排序中间或附近。故若想提高供应链整体运营效率,应着重改进卖出过程,通过降低成本来减少投入。
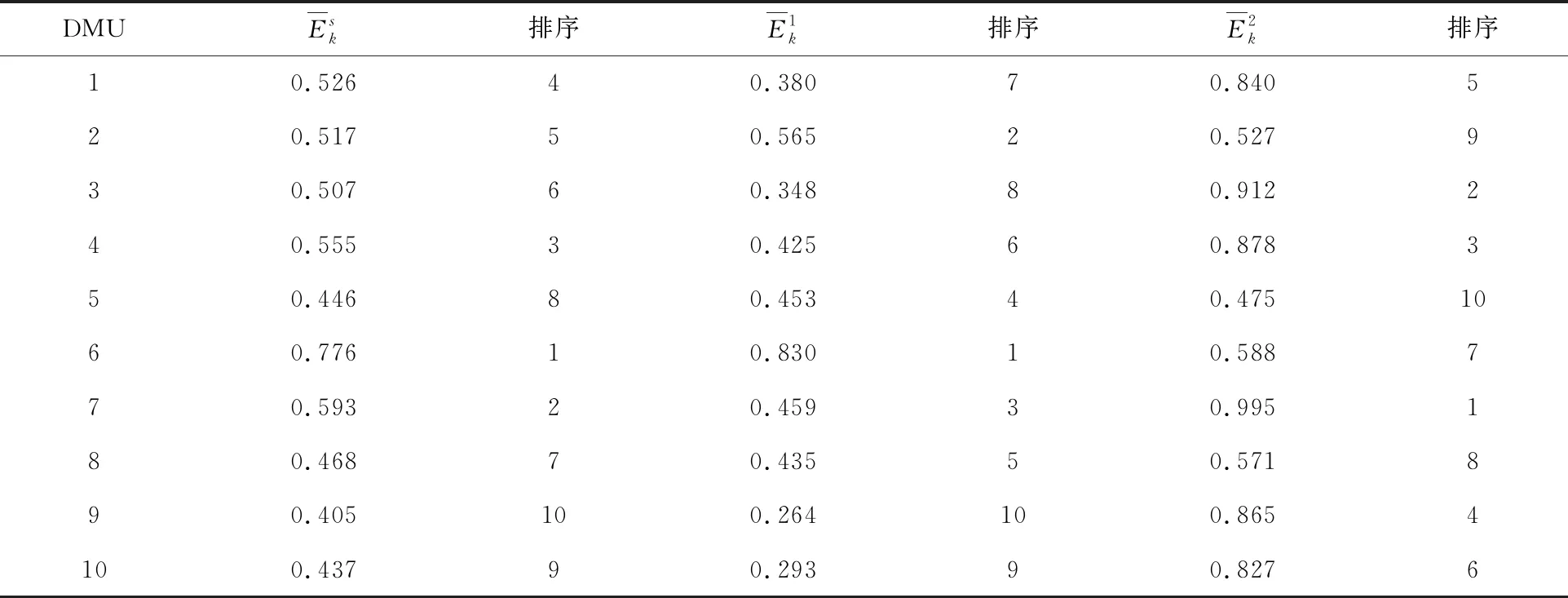
表3 整体优先模型效率及排序结果
综上,本文提出的两阶段加性交叉效率模型可以将决策单元整体分为两阶段进行测度,根据决策者偏好选择不同阶段侧重点测算效率,考虑主观因素更符合现实环境下的决策行为,并结合效率分解结果探究导致低效率的原因,便于为决策者提供更全面更深入的决策意见参考。
4 结论
传统的数据包络分析是从系统整体的角度进行的“黑箱”评价,忽略了内部的影响因素,为了观察内部运作过程,网络DEA将“黑箱”打开,对所有决策单元进行有效性评价。但二者均是从对自身最有利的角度进行评价的,结果存在一定的片面性。
本文将交叉评价方法引入加性效率模型,提出两阶段加性交叉效率评价方法来测度系统整体和子阶段的交叉效率,根据决策者偏好区分不同优先级:整体优先、阶段一优先和阶段二优先,每个决策单元系统整体的交叉效率等于两阶段的加权平均值。依照自评体系和互评体系的不同特点,对两阶段的权重取值分类后可对模型转化求解,被评价单元的最终效率是其所有交叉效率的算术平均值。

