一类多代理流水车间调度问题的合作博弈
宫 华, 孙文娟, 刘 鹏, 许 可
(1.沈阳工业大学 管理学院,辽宁 沈阳 110870; 2.沈阳理工大学 理学院,辽宁 沈阳 110159)
0 引言
流水车间调度问题是工业生产领域中研究最广泛的问题之一,是很多实际流水线生产调度问题的简化模型,在离散制造工业及流程工业中都有广泛的应用。多代理生产调度是指拥有不同客户的多个代理竞争设备资源以加工其客户的订单或工件,在生产过程中每个代理可具有各自的需求及优化目标,符合实际生产中多用户多订单的生产现状,引起了许多学者的关注[1,2]。
传统的多代理生产调度一般以生产企业为主体,考虑最大完工时间、加权完工时间和、提前/拖期惩罚等目标,根据车间生产环境、交货期、加工能力等约束条件,对代理及其工件统一调度来实现总体目标达到最优。在实际生产中,不同代理的工件可能来源于不同客户,而客户生产成本往往依赖于工件的完工时间,代理希望客户的成本尽可能最低,而企业生产能力有限,难以满足所有代理需求。在这种资源有限的情况下,代理及客户愿意通过合作结成联盟,通过在联盟内重新调度以减少总成本,并对总成本节省进行合理分配以达到最小化各自成本的目的。因此,利用合作博弈理论来研究多代理生产调度问题具有一定的实际意义。
在生产调度领域,CURIEL等[3]最先将合作排序博弈应用到单机调度问题中,他们考虑有n个代理,每个代理拥有一个待加工工件,各代理的成本为工件完工时间的线性函数,并且证明了该合作博弈核心非空。此后,合作博弈在调度问题中的应用逐渐发展起来。针对单机调度问题,在基本排序博弈模型的基础上,从加工具有准备时间[4]、恶化效应[5]、学习效应[6,7]、交货期约束[8,9]等角度进行了研究。针对并行机、流水车间等多机调度问题,也有相关的研究成果[10~13]。针对单机调度问题,CALLEJA等[14]研究了代理具有多个待加工工件的合作排序博弈,证明了在一定条件下合作博弈为平衡博弈。赵晓丽[15]针对单台批处理机上多代理生产调度问题建立合作博弈模型,证明了多代理合作博弈与工件合作博弈均不是凸博弈,而是平衡博弈。
综上可知,利用合作博弈理论研究生产调度问题的文献中,大多考虑客户或代理只有一个工件,针对代理具有多个工件的调度问题,也只是考虑单机生产环境。本文研究一类多代理流水车间调度问题,考虑拥有多个客户的代理通过合作结成联盟,各代理的客户服从代理调度,建立合作博弈模型优化生产,减少客户成本,并利用EGS规则分别对代理合作获得的成本节省以及客户合作获得的成本节省进行分配,证明了EGS规则能够产生合作博弈的一个核分配。最后通过实例验证了所建立的博弈模型及成本分配方法的有效性。
1 多代理流水车间调度问题的合作博弈模型
1.1问题描述
本文研究的具有多代理的一类流水车间调度问题描述如下:
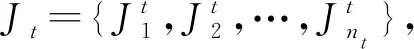
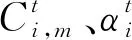
该问题的调度任务是确定各代理及其工件的加工顺序,使得总成本U最小。
对于流水车间调度问题,各道工序上工件的加工顺序不必相同,若相同,则称该调度为置换调度。当工件的加工时间和工序相关时,由于各工件在相同机器上的加工时间也相同,在任意机器上交换两个相邻工件的加工顺序,对在该机器前后加工工件的完工时间均无影响。若最优调度不是置换调度,那么按照在最后一台机器上工件的调度顺序,对前台m-1机器的工件重排序,构造出的置换调度也一定是最优调度。因此,加工时间与工序相关的流水车间调度问题一定存在一个置换调度为最优调度。本文考虑工件以置换调度进入各机器完成加工。
1.2 合作博弈模型的建立
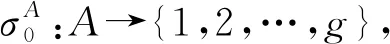
合作博弈解决的问题是:一方面在规定所有工件服从其代理按照工件最优调度排序的前提下,针对代理联盟寻找最优调度,使得代理联盟内所有工件的总成本节省最大;另一方面通过合理的成本节省分配方案,保证代理联盟的稳定性,同时保证对客户的公平性。
在多代理流水车间调度问题中,合作博弈的特征型为有序对(G,v),其中特征函数v是G的所有子集(有2|G|个)上的映射,即v:2G→R且v(Ø)=0。
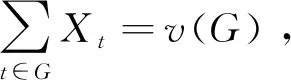
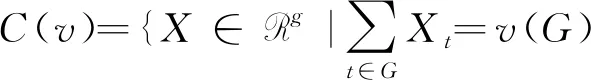
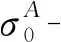
式中,v(SA)表示代理联盟SA通过联盟间合作,且代理内部工件始终按照最优调度排序加工时得到的最大总成本节省。
易知,对于加工时间和工序相关的流水车间调度问题,在置换调度σ=J→{1,2,…,n}下,各工件的完工时间为:
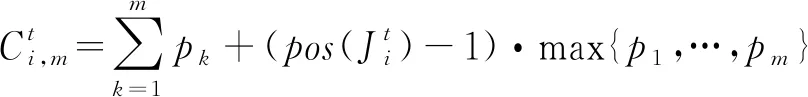
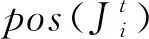
可见,对于加工时间和工序相关的流水车间调度问题,工件的完工时间只与其在调度排序中的位置有关,而与其它工件的位置无关。因此交换任意两个相邻代理加工顺序,不会影响其他代理的完工时间和成本。同样,交换代理内部任意两个相邻工件的加工顺序,也不会影响其他工件的完工时间和成本。而在一般流水车间调度问题中,由于各工件在各机器上的加工时间不同,交换代理联盟内相邻代理加工顺序,虽不会影响联盟前代理的完工时间和成本,但可能会影响其后代理的完工时间和成本。此外,交换某代理内的任意两个相邻工件加工顺序,同样也会影响该代理后其他代理工件的完工时间和成本。因此一般流水车间调度问题的合作博弈是具有外部性的。
定理1对于代理At,其工件按成本系数非增序排列的调度为At的工件最优调度。
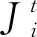
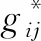
(6)
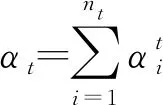
定理2对于代理联盟SA,按照各代理平均成本系数非增序排列得到的调度为代理联盟最优调度。
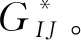
=(αJnI-αInJ)pmax
(7)
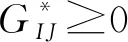
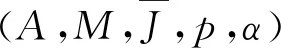
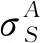
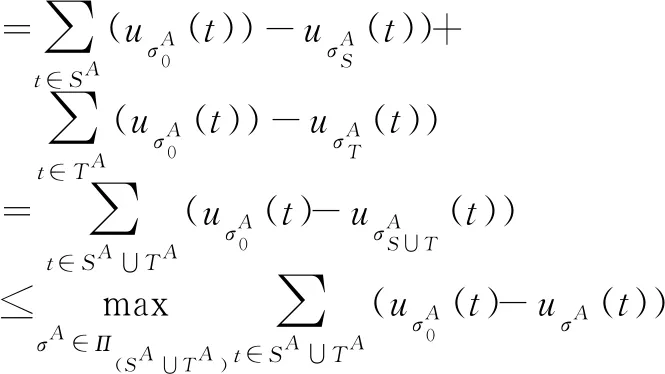
=v(SA∪TA)
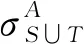
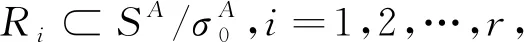
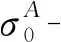
2 成本节省分配方法
本文研究的多代理流水车间调度问题的合作博弈,代理之间通过合作结成联盟,并在联盟内交换调度顺序达到成本节省,但联盟能否真正形成,取决于节省的成本分配是否合理。
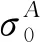
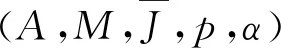
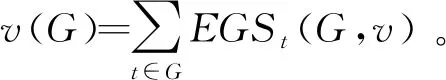
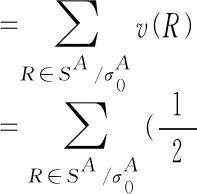
综上可知,基于EGS规则得到的成本节省分配是合作博弈(G,v)的一个核分配。
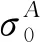
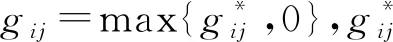
3 实例分析
本节通过例1来说明加工时间和工序相关的多代理流水车间调度问题的合作博弈模型及EGS分配方法。
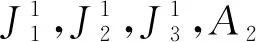
按照初始工件排序σ0、初始加工排序σ1,以及形成代理联盟后最优调度排序σ*加工时,各工件及各代理联盟成本如表1所示,其中工件成本向量按照工件在初始排序σ0中的顺序给出。
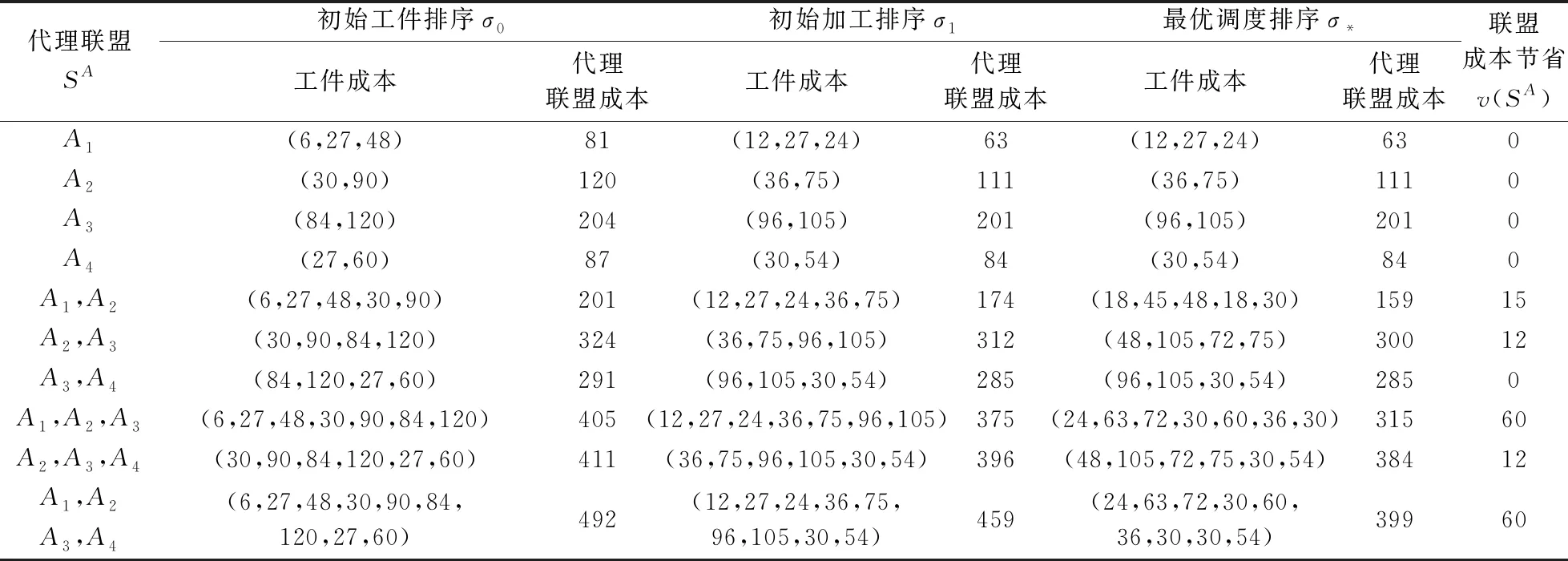
表1 I件及代理联盟在不同加工排序下的成本
由表1可知,对于任意代理联盟SA和TA,均有v(SA)+v(TA)≤v(SA∪TA),因此合作博弈具有超可加性。各代理工件通过内部合作服从代理调度获得的成本节省为:492-459=33。代理通过合作形成大联盟时达到最大成本节省v(G)=459-399=60。与初始调度排序σ0相比,最优调度获得总成本节省为:492-399=93。
由式(8)可计算出各代理获得的成本节省:
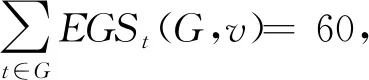
根据式(9)计算各代理工件通过内部重新排序所分配的成本节省,分别为:
由式(10)可计算出各工件的成本节省分配,具体数据如表2所示。

表2 各代理工件的成本节省分配
由表1、表2可知,工件及代理通过合作节省的成本被完全分配,且任一代理联盟分配得到的成本之和均不小于联盟的成本节省v(SA),验证了EGS分配是加工时间与工序相关的多代理流水车间调度问题合作博弈的一个核分配。由于代理A4加入任何代理联盟都不能使联盟得到更多的成本节省,因此其代理联盟节省成本分配为0。而代理A4的工件由于在加工时按照最优调度进行,带来总成本节省为3,因此每个工件成本节省分配为1.5。
4 结论
本文利用合作博弈理论对具有多个代理的加工时间和工序相关的一类流水车间调度问题进行了研究。以工件完工时间的线性函数为工件的成本,在以最小化客户成本为目标以及工件服从代理按照最优调度加工的前提下,以代理通过合作重新调度所获得的最大成本节省为联盟的特征函数,建立合作博弈模型,证明了EGS规则得到的分配为合作博弈的一个核分配。鉴于在代理内部,工件服从代理调度实际上也可以看成为工件之间形成合作,其合作机制与代理相似,考虑合作的公平性及稳定性,同样利用EGS规则分配代理工件通过合作而得到的成本节省。最后通过实例验证了合作博弈模型及成本分配方法的有效性。未来的研究工作可考虑以优化多客户非线性成本为目标,利用合作博弈理论研究车间环境更为复杂的生产调度问题。

