桑树坪井田构造复杂程度预测
——以未采区3#煤层为例
罗伟强 鲁 琪
(1.中煤西安设计工程有限责任公司,陕西 西安 710054;2.陕西煤田地质勘查研究院有限公司,陕西 西安 710021)
煤炭开采过程中,复杂的地质构造是影响高效合理采煤的重要因素之一[1]。研究者主要运用了熵函数法、灰色模糊综合评价法[2-3]对地质构造复杂程度做了大量研究,但这些方法过多局限使用于地质条件已知或半已知区,而未采区构造规律不清,科学预测难度较大。为解决这一问题,该文以桑树坪井田未采区3#煤为研究对象,应用了熵函数与模糊综合评判相结合的方法,预测了未采区构造复杂程度,旨在为矿井提供合理的采掘建议和理论指导。
1 地质概况
韩城矿区桑树坪井田位于祁吕贺山字型构造前弧东翼边缘和秦岭阴山2 个构造带之间,地质构造复杂,3#煤层已揭露断裂构造高到63 条,主要以df1、df2、df3为主,局部断层小且密集,主要分布在井田中东部及东南部位置。在整个井田范围内,褶皱构造发育,从南向北依次排列f1向斜、f2背斜、f3向斜、f4背斜、f5向斜,断裂构造多沿褶皱轴部地区展布,也是造成本区构造复杂化的主要原因之一[4-5]。
2 已采区3#煤层熵值计算
基于熵函数法对3#煤层已采区进行熵值计算,基本流程:等性网格划分→网格单元地学信息统计→网格单元赋值→网格单元熵函数计算。
2.1 网格单元划分
结合3#煤层综采的要求、煤层的赋存规律,及研究区域内构造线走向,确定了网格单元的布置形式及尺寸:200m×200m。全井田范围内共划分块网格单元1322 个。已采区占318 个网格单元,如图1 所示。

图1 网格单元划分
2.2 熵值计算
熵函数,自从玻耳兹曼(L.Boltzmann)提出以后,已在生物学、气象学等领域得到广泛应用[5]。
熵函数通常用公式(1)表示。
式中:S为系统的熵;Pi为系统中i状态出现的概率;N为系统中状态数。
为了消除系统状态不同对系统熵的影响,引入相对熵的概念,如公式(2)所示。
式中:S′为系统的相对熵;Smax为系统的最大熵值。
在信息理论中,信息熵是指信息在传播中的不确定性,高信息度的信息熵是很低的,所以,可认为熵函数的熵值越小构造越复杂,熵值越大构造越简单。
3#煤层已采区熵值的计算应遵循断层和褶皱规模越大其赋值越大的原则,见表1[6]。根据熵值计算公式(1)、公式(2)对各个网格单元的相对熵值进行计算,部分熵值结果见表2,熵值等值线图如图2 所示。

图2 3#煤层未采区预测及已采区熵值等值线

表1 熵值计算赋值原则

表2 3#煤层已采区相对熵值部分结果
3 未采区3#煤层复杂程度预测
基于回归分析与模糊综合评判相结合的方法,对该井田未采区3#煤层构造复杂程度进行预测,其主要步骤如下[8]:应用回归分析法拟选m 个评判指标,构成评判因素集,U={U1,U2,…,Um};确定每个因素在评价过程中相应的权重系数,构成因素集U上的权重集:A={a1,a2,…,an},=1;确定评判对象的评语论域,构建评语集:V={V1,V2,…,Vn};建立各评语论域里的隶属度函数,R=(fjk)m×n;选择恰当的模糊合成算子,进行模糊运算:S=A·R;按照最大隶属度原则,得到模糊综合评判结果。
3.1 回归分析筛选评价指标评价
指标的选取直接关系到未采区构造复杂程度预测的精准程度,然而未采区构造发育尚未查明,因此以已采区资料为基础,通过回归分析法,从拟选的影响构造复杂程度8 个因素中(煤层厚度di、煤层厚度变异系数Vi、上覆砂岩厚度(50m 内)Zi、上覆砂岩变异系数γi、煤层底板标高Hi、煤层底板标高变异系数ξi、顶板岩性Qi和等高线条数Ni)筛选出与相对熵值Si相关性较高的4 个变量,合理地建立未采区评语集,同时也确立相对熵值Si回归方程,为计算出未采区相对熵值Si提供理论基础。
3.1.1 煤层厚度di(m)、煤层厚度变异系数Vi
在褶皱和断层较为发育的地区,煤层厚度变化较大,会出现增厚、变薄、尖灭等现象,对同一个矿区来讲地质构造对煤层厚度变化影响的基本规律不变,因此可以根据已采区煤层厚度变化来推测未开采区域的构造特征。煤层变异系数Vi 是衡量资料中煤层厚度离散程度的一个统计量,客观反映了煤层厚度变化规律,消除了不同度量单位对多个因素变异程度比较的影响,如公式(3)和公式(4)所示。
式中:di为第i个网格单元煤层厚度;d为煤层平均厚度;n为统计点数。
3.1.2 上覆砂岩厚度(50 m 内)Zi(m)、上覆砂岩变异系数ηi
3#煤层形成于山西组第一个旋回时期,砂岩地层上覆于3#煤层顶板。在构造复杂地区局部发育有砂岩陷落空洞,导致上覆砂岩厚度发生变化。可以采用上覆砂岩厚度(50 m 内)反映该地区的构造复杂性。上覆砂岩变异系数类与煤层厚度变异系数相同。
3.1.3 煤层底板标高Hi(m)、煤层底板标高变异系数ξi
研究发现在构造复杂区,会出现煤层底板标高突变的现象[8]。一般在褶皱地区,下伏含煤地层的底板标高会随褶皱形态发生改变,在断裂构造发育区域,因断层的两盘发生错动,使两盘中的含煤地层发生错位,导致底板标高发生变化。其中煤层底板标高变异系数类同于煤层厚度变异系数。
3.1.4 顶板岩性Qi
顶板岩性往往会影响构造发育的类型,如脆性岩体受构造应力作用,易产生断裂,形成断层,而塑性岩体,易发生弯曲变形,形成褶曲。根据3#煤层顶板岩性的类型,分别赋予顶板岩性相应的量化数值,见表3[6]。

表3 3#煤层顶板岩性量化数值统计表
3.1.5 等高线条数Ni
研究发现褶皱的形态会影响研究区域的地形变化,而网格单元中等高线条数反应了该地区地形变化情况,因此拟选等高线条数为影响因素之一。
3.1.6 多元回归分析
基于SPSS 软件多元回归分析功能,以已采区相对熵为因变量,上述8 个因素为自变量,筛选了与相对熵值相关性较高的4 个变量,从而建立未采区评语集。SPSS 数据导入、处理过程及结果见表4。

表4 模型4 回归系数
通过回归分析,建立相对熵值线性方程,为未采区熵值计算提供科学依据,同时筛选了与相对熵值Si相关性较高的4个影响因素,最终确立了评语集:U=(Si,Ni,Zi,Vi,Qi)。
3.2 评语等级划分标准
基于《煤矿地质工作规定》有关地质构造的4 类划分法,确定评语等级标准,将3#煤层未采区构造复杂程度划分为4种等级,V={V1,V2,V3,V4},V1简单,V2中等,V3较复杂,V4复杂。根据数理统计方法,并结合井田地质特点,得到各评价指标造复杂程度分类标准,见表5。

表5 3#煤层各评价指标造复杂程度分类标准
3.3 权重
权重是决定评价指标对评价结果影响的主要因素,利用灰色关联的分析法确定各个评价指标的权重值。在各评价指标中,相对熵值Si综合反应了构造复杂程度,因此以相对熵值Si为参考数据列,其他4 个评价指标作为比较数据列,再进行权重计算。具体做法:评价指标的原始数据初始化、均值化处理→各比数据较列与参考数据列绝对误差值计算→确定最大和最小绝对差值→关联系数和关联度计算→归一化处理→得出权重系数。各评价指标关联度和权重系数计算结果具体见表6。
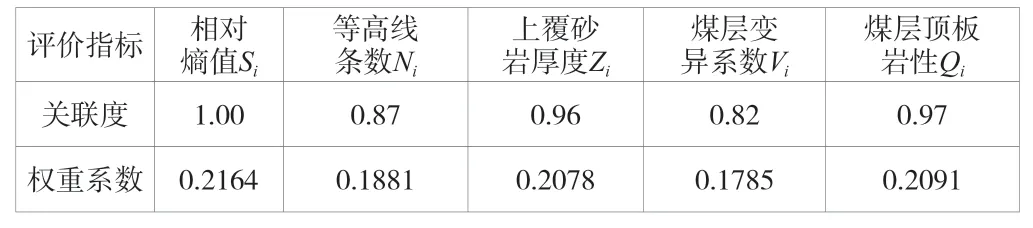
表6 评价指标关联度和权重系数
3.4 隶属度函数
结合表5 构造复杂程度与各个影响因素之间的关系,3#煤层采用“降半梯形”建立隶属度函数结果如下[1,5],以等高线为例构造隶属度函数,构造简单(f11(x))、构造中等(f12(x))、构造较复杂(f13(x))、构造复杂(f14(x))的函数具体形式如公式(5)所示。
3.5 模糊运算
某网格单元关于构造复杂程度等级j的聚类系数如公式(6)所示。
式中:fij(x)为单元格第i个参数属于第j类的函数;ηi为单元格第i个参数的权重值;σij为网络单元格聚类系数。
通过计算网格单元的聚类系数,得到每个单元格的构造复杂程度隶属度。根据网络单元的4 个评语集别的隶属度关系确定网格单元的构造复杂程度级别。遵循最大隶属度原则,确定网格单元最终评价结果。根据评价结果绘制出3#煤层未采区构造复杂程度预测结果图,并统计出各个预测等级所占的百分比。
3.6 未采区3#煤层预测
根据图2 和表7 可知,较复杂及复杂区块占未采区的67.61%,所处位置主要集中在已采区3#煤层的中南部、北部区域及f1向斜、f2背斜、f4背斜、f5向斜所在区域。基本简单、中等的区块分布杂乱,主要集中在中部、南部少数区域及北部边缘地带。

表7 未采区 3#煤层构造等级百分比
4 结论
3#煤层整体分析表明复杂区块主要集中在北区df1断裂构造区域、中区f4背斜区域、南区f1向斜与f2背斜之间区域。其中,已采区相对熵值小于0.7 的构造复杂区块主要分布在南区、中区局部区域内。未采区构造复杂区块主要集中在中南部、北部区域及f1向斜、f2背斜、f4背斜、f5向斜所在区域,简单、中等的区块分布杂乱,主要集中在中部、南部少数区域及北部边缘地带。
3#煤层未采预测结果与实际钻孔揭露情况吻合度较高,预测结果明确了各构造等级的分布区域,为煤矿生产部署提供一定参数。
——以中国、新加坡教材的三角形问题为例

