网络安全态势预测技术研究综述
向城成 吴春江 刘启和 周世杰
(电子科技大学信息与软件工程学院 四川 成都 610054)
0 引 言
大数据时代的到来使得各个行业和领域与互联网紧密结合,互联网思维亦成为现代社会必不可少的思维方式,它与各传统行业相结合,为各行业的发展提供了巨大驱动力,与此同时也对网络的安全性有了更严格的要求。无论是企业公司,还是学校公务机关都可能有自己的网络结构,部署包括交换机、路由器、服务器等重要设备,相关单位会使用网络传输各种数据、信息,一旦网络的安全受到威胁,将会对整个单位的利益造成巨大的损失[1]。
互联网虽然加快了各行业融合协同发展,但也使网络安全面临了更多的问题和威胁。仅2018年上半年,网络攻击相关的互联网安全事件就层出不穷,如俄罗斯电网攻击事件、美国300多所大学受伊朗黑客攻击事件、美国Exactis公司数据泄露事件、安德玛健身追踪应用MyFitnessPal数据泄漏事件、恶意软件VPNFilter事件等。网络安全事故的频繁发生引发了各行各业的高度重视,学界对网络安全态势(Network Security Situation,NSS)的研究越发深入,一种基于NSS智能感知、评估、预测的新型网络安全防护体系应运而生。
网络安全态势预测(Network Security Situation Prediction,NSSP)首先采集一段时间中的攻击事件,根据攻击事件的种类、频率等,然后关联融合分析后得到评估的态势值,利用过去时间的攻击事件信息及态势值可以对未来的NSS发展趋势进行预测,能够为网络管理人员提供必要的数据与信息支持,使网络管理人员能够采取必要的网络安全防护措施,制定合理的网络安全防护方案,以做出有效的网络安全防护决策。
1 常见的网络安全态势预测方法
网络安全态势通过历史数据对未来的态势值进行预测的方法有很多,根据数据的特性和使用方法的领域可对方法进行分类。当NSS数据具有少数据、贫信息、不确定性等特点时,可将使用的方法分类为“不确定推理理论”,当数据为其他正常完整数据时,可将预测方法按方法类型分为“机器学习人工智能方法”和“神经网络方法”。因此常见的NSSP方法通常可分为以下三大类:不确定推理理论方法、机器学习及人工智能领域方法、神经网络方法,及多种优化调整的混合预测方法和模型。本节主要介绍三类常用的预测方法,罗列其在各行业、各领域的应用,并阐述在态势预测领域的应用策略或方案。
1.1 不确定性推理理论
在NSSP领域,进行数据预测通常会遇到NSS信息、数据不完备或缺失的情况,这种情况下可考虑使用不确定推理理论的方法,利用不完备、不确定数据,对未来态势值进行合理的预测和推断。在NPPS领域,最常用的不确定性推理理论方法包括灰色系统理论和D-S证据理论。
1.1.1灰色系统理论
灰色系统理论[2]是于20世纪80年代提出的一种着重于不完备数据信息的方法,针对不完备信息(贫信息)、小数据的建模分析方法,通过生成、挖掘、提取有用的信息来处理仅部分信息已知的不确定系统[3],可根据仅部分已知信息正确描述演化规律或变化过程。
从灰色系统理论提出至今,在数据预测领域许多专家学者对其进行了深层次的研究和讨论,推动灰色系统理论在数据预测应用层面的发展[4],通过建立灰色预测模型在各种应用场景进行预测的研究应用。比如杨文博等[5]为了验证灰色预测模型在运营桥梁的基本状况,运用灰色系统理论的原理,以某正在使用的桥梁为基础,基于GM(1,1)进行建模与分析,并将预测数据与实测数据进行对比分析,得到较为精准的结论以证明灰色预测模型可以对桥梁状况进行预测;Liu等[6]基于GM(1,1)对GDP指数预测,并提出终点优化的调优策略,使GM(1,1)性能有所提升。
而利用灰色系统理论对NSS的预测方面,灰色系统理论进行态势预测可建立应用面较广的GM(1,1)及精度更高的GM(1,N)[7],利用没有规律或规律表现较弱的数据,然后对其整理规整,得到它的变化规律,这便是产生灰数据序列的过程,灰数据序列可以利用生成方式削弱它的随机性从而体现规律性,通常采用累加、累减、加权邻值等方式,这样生成较有规律的生成数,建立一阶微分拟合方程,然后利用一元线性回归求得估计值以完成预测。GM(1,N)依然采用累加、累减、加权邻值的生成方式,建立多因子数列微分方程,利用一元线性回归方法求得估计值以完成预测。
1.1.2D-S证据理论
D-S证据理论(Dempster/Shafer Evidence Theory)是由Dempster提出,由Shafer进一步推论发展起来的不确定推理理论,与灰色系统理论相似,同样也有表达不确定信息的能力,其核心思想便是采用“区间估计”的方法来对不确定信息进行描述,最终确定信任区间以获得预测结果。
D-S证据理论同样被广泛用于数据预测领域,在各类预测的应用场景中发挥了至关重要的作用。比如Gao等[8]利用D-S证据理论建立了瓦斯突出数据的预测模型,有效防止瓦斯突出可能带来的巨大破坏;Bauer[9]通过使用多个预测模型作为证据,结合D-S证据理论对保健结果进行有效预测。
在NSSP领域,利用D-S证据理论,构建基于D-S证据理论的预测模型以完成预测[10]。利用D-S结合攻击、防御及整体性的NSS数据,利用该方法善于处理不确定数据的特性,并且基于D-S证据理论进行态势评估(假设空间P)、安全状态概率分配(Mass函数)、融合计算(合成规则)等建立NSSP模型,通过攻击态势、防御态势、总体态势构建D-S证据理论的假设空间、Mass函数及合成规则,最后确定信任区间的具体过程如图1所示[11]。

图1 基于D-S证据理论建立的NSSP模型
1.2 机器学习及人工智能领域方法
在NSSP领域,进行数据预测时在数据完备的情况下,可考虑采用机器学习及人工智能领域的预测方法,通过历史数据序列对未来时间态势值进行预测,该类方法用在态势预测中使用率最高的主要包括:支持向量机、隐马尔可夫模型、卡尔曼算法等。
1.2.1支持向量机
支持向量机(Support Vector Machine,SVM)在机器学习与人工智能领域的应用较为广泛,是一种通常用来解决二分类问题的有监督学习的算法。
支持向量机在各种预测场景下的应用也成为近年来的热门研究点,结合一些参数优化算法取得表现不错的SVM预测模型。比如Duan[12]利用PSO优化的SVM模型即PSO_SVM,对一定时间内的车流量进行预测;Alam等[13]利用多阶段分类的SVM用于肺癌的预测。
在NSSP领域,基于SVM建立NSSP模型可首先创建基于时间维度的原始NSS数据序列,然后结合SVM的调参优化策略,利用时间数据序列及SVM参数调优等处理,得到基于SVM的NSSP模型。SVM训练相对容易且能够方便地转换为高维数据,SVM也能够直接地控制在分类时的平衡复杂性及错误问题,利用SVM进行NSSP的可行性和实用性较高[14]。
1.2.2隐马尔可夫模型
隐马尔可夫模型(Hidden Markov Model,HMM),“隐”表示其有未知参数,HMM因其优越性被广泛应用在语音识别、数据预测、状态评估、分类问题、入侵检测等领域[15],并取得了不错的效果。
隐马尔可夫模型在数据预测方面有较广泛的应用。比如Wang等[16]使用堆叠式集成方法从HMM谱图预测DNA结合蛋白;Chen等[17]使用基于XGBpred的极限梯度增强和基于HMMpred的隐马尔可夫模型。在10倍交叉验证测试中,XGBpred和HMMpred在最先进的方法Geno2pheno和G2p_str上均达到了更高的特异性72.56%和72.09%,相同的灵敏度为93.73%。
在NSSP领域,通过HMM构建NSSP模型可表示为一个五元组[18]:(1) 隐含状态集合:不可通过直接观察得到的,可表示为NSS的状态安全等级;(2) 可观察状态集合:可选用与隐含状态关联的如系统日志、防护设备日志等作为观测向量集;(3) 状态转移概率矩阵:在隐含状态集合下不同安全等级的转移矩阵;(4) 可观察状态转移概率矩阵:为在不同可观测向量与隐含状态等级的关系转移概率矩阵;(5) 初始概率矩阵:初始时刻所处的观测向量与隐含状态等级。利用HMM构建NSSP模型进行高效、精准的预测[19],得到未来时刻的安全状况以及时采取防护策略[20]。
1.2.3卡尔曼算法
卡尔曼算法,也称卡尔曼滤波算法或线性二次估计,以产生更多的未知变量估计,通过估计每个时间帧变量的联合概率分布,对系统状态进行最优估计,得到预测结果。
卡尔曼算法能够有效对系统状态进行最优估计以求得预测结果,因此它常被应用在数据预测领域。比如Mo等[21]使用卡尔曼滤波算法对锂离子电池的剩余寿命进行预测;Emami等[22]基于卡尔曼滤波算法建立短时间交通流量模型,对交通流量数据进行最优估计得到预测值。
在NSSP领域,卡尔曼算法利用描述状态方程、观测方程[23]进行NSSP获得相对精准的预测结果,其中状态方程包括:状态向量转移、状态转移矩阵、状态向量等;而观测方程包括:观测噪声、观测向量等,利用基于卡尔曼算法建立NSSP模型,获取原始数据值,并利用算法结合数据进行预测[24];利用卡尔曼算法建立NSSP模型,卡尔曼算法的预测结果和实际结果趋势一致,证明了卡尔曼滤波算法在NSSP中的可行性[25],且通常卡尔曼算法的预测精准性要高于单纯的GM(1,1)模型等[26]。
1.3 神经网络方法
在NSSP领域,在进行数据预测且数据完备时,神经网络方法是一种高效、精准的预测方法,同样通过历史数据序列对未来时间态势值进行预测,该类方法用在态势预测中使用率最高的主要包括BP神经网络、RBF神经网络、RNN神经网络等。
1.3.1BP神经网络
BP(Back Propagation)神经网络是20世纪80年代,Rumelhart等提出的一种信号向前传递、误差向后传递的多层神经网络学习方法,可通过权重调整使输出的预测结果更加接近于期望值,通常BP神经网络包含三层结构,分别是第一层输入层、第二层隐含层、第三层输出层。
BP神经网络在数据预测领域有良好的表现效果,也可用于分类问题、计算机视觉、机器人技术等领域。比如,Liu等[27]利用分段学习的双层BP神经网络,对道路通行流量进行精准的预测取得了较好结果;Wu等[28]提出了一种基于反向传播BP神经网络的预测工具GAIFOA-BP,用于预测在不同储油条件下FPSO模型相关位置的应变值。
基于BP的NSSP模型首先利用现有的数据找到输入、输出的权值关系,在NSSP领域可利用BP神经网络,建立NSSP模型[29],包括原始NSS数据的输入层、映射层、输出层如图2所示。架构输入层为对应节点的NSS原始数据;映射层即为BP神经网络,映射层的BP结构即获取数据输入并加权计算,通过BP结构的隐含层激活函数后映射成输出,获取数据再次通过加权、计算、映射得到输出。

图2 基于BP神经网络的NSSP预测架构
1.3.2RBF神经网络
RBF(Radial Basis Function)即径向基神经网络,是使用RBF作为激活函数的人工神经网络结构,RBF结构的输出为输入的RBF函数与神经元参数的线性组合。
RBF神经网络在函数近似、时间序列预测、分类等应用场景下表现良好,RBF神经网络也是数据预测领域一个较精确高效的方法。比如J神经网络(基于递归粒子滤波的基于Rbf网络的测量数据时间序列预测)领域的新研究和发现的详细信息[30]。Li等[31]使用了优化后的径向基(RBF)神经网络开发了一种通用的剩余保质期数据预测模型,该模型通常用于采摘后的可食用葡萄,以实现比当前保质期预测方法更准确的数据预测。
在NSSP领域,通过训练RBF神经网络,找到前序数据与后续数据存在的映射关系,然后调整前序数据的个数,探索不同的NSSP结果,态势数据的值可以视为非线性的时间序列,RBF神经网络可以实现通过前序N个数据和后续M个数据,找出在NSS数据的非线性映射关系,基于RBF结构进行NSSP流程如图3所示。研究了基于RBF的NSSP预测结构,利用RBF及BP两种网络结构得到NSSP结果,证明在NSSP领域RBF的预测结果比BP网络要好[32]。

图3 RBF网络结构进行NSSP流程
1.3.3RNN神经网络
循环神经网络(Recurrent Neural Network,RNN)是神经元相互之间连接形成一个有向环的人工神经网络,它展示基于时间序列的动态行为,广泛地应用在对序列态势数据的处理方面。
由于循环神经网络善于处理任意长的数据,它在数据预测领域有较广泛的应用。比如Ramakrishnan等[33]通过历史网络流量及RNN预测未来流量数据;Hagos等[34]通过RNN对TCP传输状态进行预测。
在NSSP领域,由于NSS有以时间为序列来预测的特点,提出以RNN对NSS数据进行预测,利用RNN能够充分利用任意长度、以时间为序列的NSS数据信息,能够有效保证利用RNN进行NSSP的预测准确性[35],NSS数据的特点以及RNN进行数据预测的特性决定了两者能够完美结合以得到高精度高效率的预测结果。
2 方法特性、对比及其优缺点
经过十余年的发展,在常见的NSSP方法取得了巨大的成就同时,学者们也发现了一些诟病,如需要参数优化、模型调优、预测精度不足等,该节横向对比三大类预测技术,并横向对比了具体各类别的预测技术,分别详细阐述态势预测方法的优缺点及其在网络安全态势预测中表现的优劣之处,如表1所示,能够高效合理地选择相应的预测方法完成对NSS数据的预测。
2.1 不确定性推理理论类
两种方法的优缺点横向对比如表2所示。

表2 两种不确定性推理理论方法优缺点横向对比
2.1.1灰色系统理论
利用灰色系统理论建立预测模型主要优势是可以利用小数据、贫信息来进行预测工作,是在数据量小、数据不完整的场景下的不二之选;GM(1,1)与GM(1,N)通常对未来短时预测的情景下表现最好;利用这些模型的运算过程比其他模型更为简单。对于单调递增或单调递减的数据序列,能达到很好效果,但在波动变化、不规则变化、变化明显的非线性数据序列的预测精度较低且误差较大。
2.1.2D-S证据理论
D-S证据理论同灰色系统理论一样,对于贫信息、小数据的描述直接方便,且该理论还有综合不同数据源的特性。但其在理论论证上处于劣势,没有强大的理论支撑其合理有效性;而且其对证据要求独立,但在很多时候,数据间确实存在关联。
2.2 机器学习及人工智能类
三种方法优缺点横向对比如表3所示。
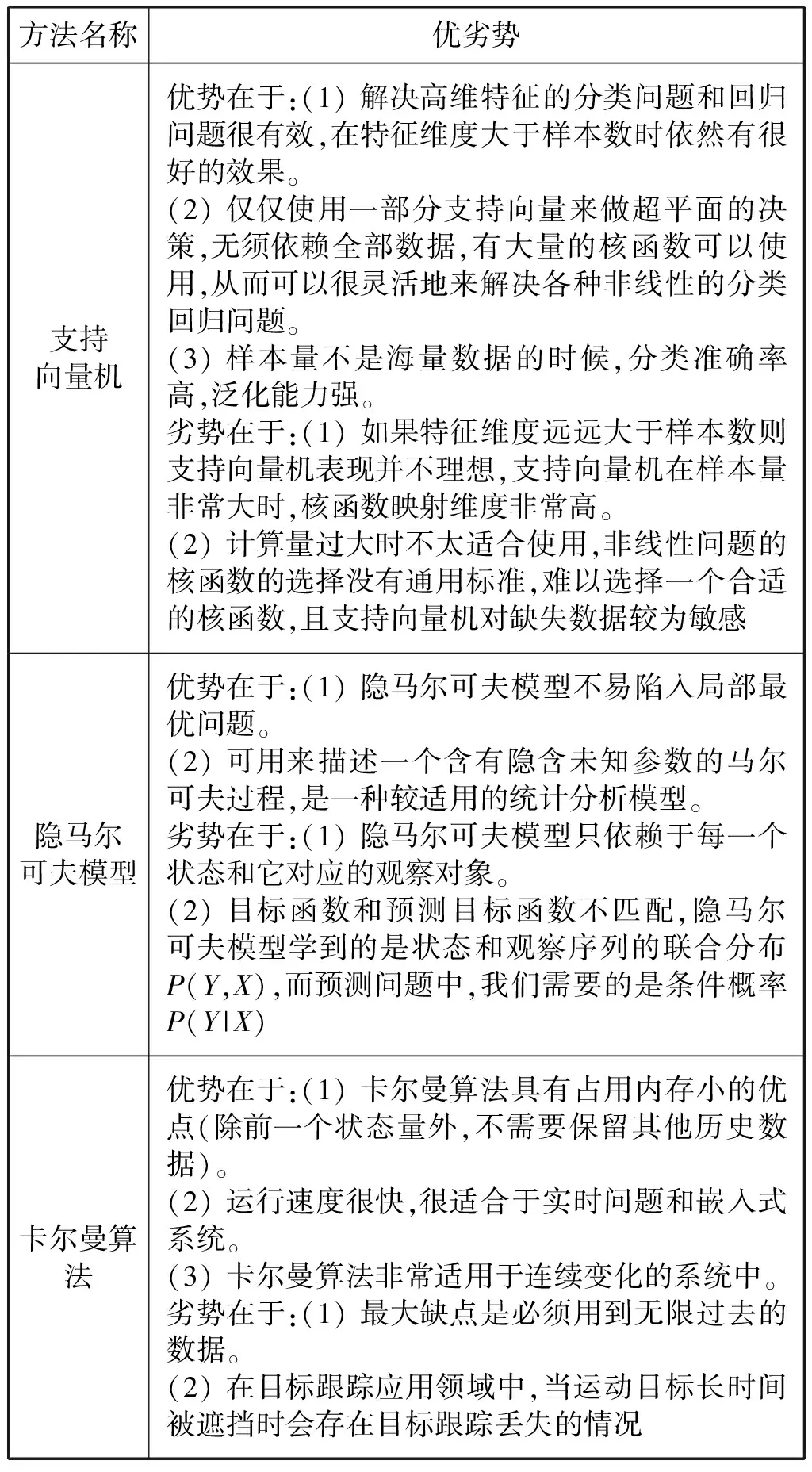
表3 三种机器学习及人工智能方法优缺点横向对比
2.2.1支持向量机
SVM在数据预测领域有广泛应用,其泛化能力强,在新样本中有较强适应能力;利用有效的已知算法发现目标函数的全局最优解,能够有效解决陷入局部最优的主要问题;当然SVM还能有效处理小样本数据、高维度数据、非线性数据等。这些优势都为其在数据预测领域的发展提供了推动力。但支持向量机也有许多诟病,首先在观测样本过多的情况下效率较低,对大规模训练样本难以进行;在核函数的寻找方面,对于非线性模型无统一标准,较难寻找到合适的核函数取得良好的性能表现;缺失值对于SVM的性能有至关重要的影响。
2.2.2隐马尔可夫模型
隐马尔可夫模型是通过转移概率及可观察的表现概率进行建模,统计共同出现概率而非采用条件概率或局部归一化,因此不易陷入局部最优问题。建立基于HMM的预测模型可以反映观察状态和实际状态之间的转化规律及概率关系。在预测场景下,隐马尔可夫模型学习的通常是隐含状态集合、可观察状态集合两者的联合分布,而在预测中需要的是条件概率分布;在一些场景下,HMM对独立性的假设较为严格,会导致模型设计有局限性。
2.2.3卡尔曼算法
卡尔曼算法可对需要预测的相关系统状态进行最优估计。但它仅利用历史数据进行预测并未考虑动态的环境外围因素对NSS数据值的影响;卡尔曼算法还有预测精度略偏低的现象。
2.3 神经网络类
三种方法的优缺点横向对比如表4所示。

表4 三种神经网络方法优缺点横向对比

续表4
2.3.1BP神经网络
BP神经网络结构实际上实现的是从输入到输出的映射过程,网络结构如前文提到的包括三个层次,一个显著的优势是BP结构的非线性映射能力强;与SVM一样,有泛化能力较好地特性,对新样本能够较好的适应;BP结构容错性也较好,局部出错不会对后续的全局预测结果产生大的波及。与SVM相反,BP结构容易遇到局部最优的问题而导致训练不成功;其优化的目标函数通常情况下是复杂的,这样会导致整个结构的效率低下;由于不能用步长迭代的传统方法,BP神经网络需预先设定步长更新规则,这样的操作同样会导致BP神经网络低效;其结构还时常面临结构不统一、过度依赖样本、过拟合等问题。
2.3.2RBF神经网络
与BP网络结构相似,RBF网络结构实现也是输入到输出的映射过程,RBF在映射方面有能力强表现良好的特点。但与BP结构不同的是,学习的收敛速度明显快于BP结构的收敛速度,且RBF结构通过唯一最佳逼近,不会存在局部最优的问题。RBF神经网络还在分类问题中表现良好。RBF网络结构存在最主要的问题是理论研究不足,无法合理阐述RBF的推理推导理论和过程、依据等;将特征都转化成数字,通过数字的处理计算得到结果,这可能导致信息缺失的后果。
2.3.3RNN神经网络
RNN神经网络最大的优势在于处理任意长度输入、输出的能力,且RNN利用时间序列数据,这也是适用于网络安全态势预测的重要原因;但RNN与大多数神经网络结构一样有些缺点,如训练难度较大且参数过多调参有难度等。
3 混合模型及优化策略
可以看出传统的网络安全态势预测技术很多时候有表现不足的地方,如局部最优、精度较低、依赖性大、过拟合等问题,因此许多专家学者基于不确定性推理理论、机器学习人工智能方法、神经网络方法为基础建立混合模型或调优。本节将介绍一些混合模型或优化后的预测模型,能够为预测提供精度更高、效率更高的方案。
3.1 不确定推理理论类
3.1.1灰色预测模型结合Markov链
前文提到灰色预测模型具有小数据贫信息预测、结构简单、短时预测效果好等特点,顾兆军等[36]提出了将灰色预测模型与Markov相结合的NSSP模型,利用Markov模型强随机性的特点,将Markov加入到模型中,能够有效修正预测模型中结果值和实际值之间的误差,作者基于此提出了一种实时NSSP流程如图4所示。
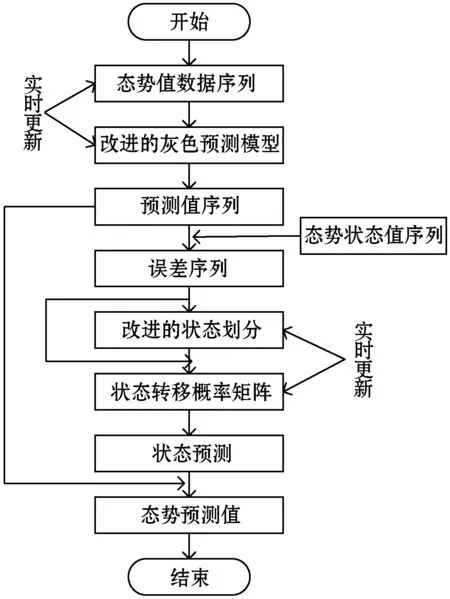
图4 改进的灰色模型+Markov实时NSSP流程
3.1.2灰色预测模型结合BP神经网络
邓勇杰等[37]提出用灰色理论结合BP网络结构建立效果更优的灰色神经网络NSSP架构,其结构具有计算方便、结构简单的特点,而BP网络结构有非线性映射能力强、泛化能力强、容错性及自学习自适应的特点,因此作者提出利用灰色预测模型的小数据贫信息特点,结合BP结构强映射能力进行残差预测,对NSSP结果值进行残差修正,从而获得更精确的预测结果,建立性能优于原始灰色模型的灰色BP网络NSSP模型,改进的灰色BP神经网络NSSP模型具体步骤如图5所示。

图5 改进的灰色BP神经网络模型NSSP步骤
3.1.3自适应的灰色预测模型
Zhu等[38]提出了采用自适应灰色参数、等维灰色填充(Equal Dimensions Grey Filling,EDGF)来建立改进的自适应灰色分析预测模型。Verhulst模型是灰色理论中主要部分之一,作者采用自适应参数的方式来确保灰色Verhulst模型精度;在精度得到保证后采用等维灰色填充构造EDGF-Verhulst模型来抵抗未知因素对模型精度的影响。
3.1.4D-S证据理论的组合预测
由于NSSP受诸多不确定因素的影响,胡海亮[39]利用D-S证据理论建立组合模型,作者首先确定了单项预测模型权重,然后对历史权重进行融合以得到预测权重,并对权重的提取和权重的融合进行了细致的描述,仿真实验证明了高精度的D-S理论组合模型进行NSSP是有效可行的。
3.2 机器学习及人工智能类
3.2.1遗传算法优化的SVM模型
郭政等[40]提出以遗传算法(GA)优化的SVM即GA_SVM模型,GA_SVM模型同样以NSS数据来训练SVM网络,通过遗传算法来获取合适的SVM预测模型参数,在SVM的预测过程中,惩罚因子、核函数的选择对SVM预测结果有着决定性的影响,利用GA的自然进化过程,以此搜索最优解来选取惩罚因子和核函数,能够有效排除因人为选定参数带来的精度影响。
3.2.2引力搜索算法优化的SVM模型
陈玉鑫等[41]提出以引力搜索算法(Gravitational Search Algorithm,GSA)优化的SVM网络安全态势预测模型GSA_SVM模型,与GA_SVM模型相似,同样采用的是找到SVM最优参数的策略,不同的是GSA_SVM模型采用引力搜索算法不断变化参数以找到最优参数,然后根据GSA择取的最优参数来构建SVM的NSSP模型,与原生SVM相比,预测模型GSA_SVM具有高精度、高效率等特性。
3.2.3粒子群算法优化的SVM模型
陈善学等[42]提出以粒子群算法(Particle Swarm Optimization,PSO)来对SVM预测模型进行参数寻优,建立一种累加PSO_SVM的NSSP模型,思想与GA_SVM、GSA_SVM类似都是利用算法的寻优特性对SVM参数优化,该模型的数据序列累加策略能够减少不规则数据对预测结果的扰动和影响。
3.2.4模拟退火及BW算法优化的HMM模型
李方伟等[43]利用模拟退火算法(Simulate Anneal,SA)及Bauw_Welch(BW)算法的结合来解决隐Markov预测模型参数难以配置的问题,能够建立精度更高、收敛速度更快的HMM预测模型,利用入侵检测数据有效对NSS数据进行预测。
3.2.5最大熵法优化的HMM模型
詹雄等[20]提出结合最大熵算法(Maximum Entropy Method,MEM)对态势值预测进行统一的判定,有效提高动态、实时的NSSP态势数据值的准确性。
3.2.6加权优化的HMM模型
Liang等[15]利用多尺度熵的方法,基于加权HMM构建NSSP模型,多尺度熵用于解决训练数据的问题,并对HMM传递矩阵参数训练进行了优化,利用NSS历史数据特征间的关联对未来NSS数据进行预测。
3.2.7灰色关联熵卡尔曼算法
Wang等[26]利用灰色关联熵分析法分析影响预测结果的相关性,根据选择的关键影响因素建立相应的过程方程和预测方程,通过一种改进的迭代计算方法,引入具有自适应鲁棒性能的新型拼接卡尔曼滤波算法,提高锂离子电池组的充电状态预测精度,实验证明了灰色关联熵卡尔曼算法比灰色系统理论预测精度更高。
3.3 神经网络类
3.3.1改进贝叶斯正则化的BP神经网络
周显春等[44]提出一种基于改进的贝叶斯正则化的BP网络结构,模型应用了BP网络结构非线性映射能力强的特点,同时作者还使用了层次化的预测思想,总结如图6所示。

图6 BP网络结构分层NSSP思想步骤
3.3.2MEA-BP神经网络模型
思维进化算法(Mind Evolutionary Algorithm,MEA)是一种1998年被提出的通常应用于对人工神经网络结构优化的算法。在NSSP领域,Xiao等[45]提出基于MEA-BP模型对NSS数据进行预测,NSS数据有着非线性时间序列的特点,为了解决BP网络结构的局部最优解、多次迭代、效率低下的问题,作者优化了其权重和阈值,使用基于思维进化算法优化的MEA-BP模型进行未来的NSS数据预测,有效提高了预测准确率和效率。
3.3.3RBF参数的改进优化
孟锦等[46]提出一种利用混合递阶遗传算法(Hybrid Hierarchical Genetic Algorithm,HHGA)对RBF结构进行参数选择优化的HHGA_RBF模型,能够利用样本数据确定RBF结构及参数,预测精度较高。
赖智全[47]结合人工鱼群算法(Artificial Fish Swarm Algorithm,AFSA)、粒子群算法(Particle Swarm Optimization,PSO),提出一种利用两者结合来对RBF结构进行参数寻优,从而构建一个高效的NSSP模型IAFSA_PSO_RBF预测模型。
3.3.4聚类和自适应的RBF改进优化
甘文道等[48]提出基于资源分配网络(Resource Allocating Network,RAN)对网络安全态势样本数据进行聚类,并用改进粒子群算法(Modified Particle Swarm Optimization,MPSO)来进行参数寻优构建NSSP模型。
李方伟等[49]提出自适应聚类(Adaptive Clustering,AC)的RBF神经网络NSSP模型,在反映总体变化趋势的同时能够有效提高精度。李方伟等[50]又提出可使用吸引力传播(Affinity propagation,AP)对NSS数据样本进行聚类,使用差分进化(Differential Evolution,DE)来优化RBF神经网络,构建一种基于APDE_RBF网络结构的NSSP模型。
3.3.5小波神经网络(WNN)的定量预测
Zhang等[51]利用改进生态位遗传算法(Improved Niche Genetic Algorithm,INGA)构建了基于小波神经网络(Wavelet Neural Network,WNN)的网络安全态势预测模型,该模型采用具有较强非线性能力和容错性能的WNN。最终仿真结果表明,所提出的INGA-WNN预测模型具有更快的收敛速度和更高的预测精度,能够对网络安全态势进行更精准和更快速的预测。
4 应用场景及实用性分析
使用于态势预测的网络安全态势数据通常包括(列举数据含适用面最广的KDD1999、CIC-IDS-2017或自行数据采集)。
(1) 以KDD1999数据集为例:TCP连接基本特征、TCP连接的内容特征、基于时间的网络流量统计特征、基于主机的网络流量统计特征。
(2) CIC-IDS-2017入侵检测评估数据集为例:CICIDS2017数据集包含良性和最新的常见攻击,类似于真实的真实数据(PCAP)。它还包括使用CICFlowMeter进行网络流量分析的结果,并基于时间戳、源和目标IP、源和目标端口、协议和攻击(CSV文件)标记流量,也可以使用提取的特征定义。
(3) 自行数据采集:通常数据采集是指从各种设备当中获取各种与网络空间安全的相关数据,如系统日志、告警、信息、网络拓扑等。
网络安全态势数据预测流程如图7所示。

图7 网络安全态势数据预测流程
4.1 不确定性推理理论类分析
不确定性推理理论可以使用信息部分清楚、部分不清楚并带有不确定性现象的数据,通常不需要大量样本,且数据不需要有规律性分布,通常计算工作量小,预测精准度较高,对于不确定性问题的描述很灵活和方便。
由于网络安全态势数据的采集需要通过软硬件技术的结合来产生和收集网络安全数据,可能导致网络安全态势数据信息存在不确定性,部署的态势数据搜集工具可能存在时间、空间、部署成本等因素的局限性因而导致数据样本数量较少,且网络安全态势数据通常呈不均匀分布。综上所述,不确定性推理理论适用于小数据、贫信息时候的网络安全态势预测工作。
4.2 机器学习及人工智能类分析
通常情况下机器学习及人工智能类方法可以解决高维特征数据,机器学习及人工智能类方法可以解决小样本问题、非线性问题、不易陷入局部极小值问题,且泛化能力比较强;其中卡尔曼算法还具有占用内存小的优点,运行速度很快,很适合于实时问题和嵌入式系统。
由于网络安全态势数据通常有高维度的特征,可能由于部署的态势数据搜集工具存在时间、空间、部署成本等因素的局限性因而导致数据样本数量较少,所以面临小样本问题,通常情况下网络安全态势数据呈现非线性变化。综上所述,机器学习及人工智能类方法适用于小样本、非线性的安全态势预测工作。
4.3 神经网络类分析
神经网络能够自适应、自主学习,不断地调整神经网络中的参数以达到最符合期望的输出,并且其非线性映射能力,有强大的理论支撑,个人神经网络预测方法不易陷入局部极小问题,具有较强的输入、输出映射功能。
由于网络安全态势数据通常呈非线性变化,通常还是一种从输入到输出的映射过程,网络安全态势数据通常呈不均匀分布,但如BP神经网络拥有强大的理论支撑能够更好地解释态势预测的过程及结果,RBF神经网络无局部极小问题可以有效解决控制数据呈不均匀分布带来的影响。综上所述,神经网络类方法适用于安全态势预测工作。
5 结 语
NPPS相关技术经过多年的发展取得了较大的进展,在多种原有的预测模型基础上进行优化,构建混合模型提高预测精度或效率,或是创新选用一些相对冷门的预测模型尝试对NSS进行预测。
调查研究发现还有许多的数据预测方法没有被尝试使用在网络安全态势预测领域,为了适应目前网络安全态势的需求和发展,网络安全态势预测技术需要考虑以下方向的发展:
(1) 将更多其他领域发展成熟的数据预测方法尝试在NSSP领域进行应用,取得更好的效果。
(2) 选用相应算法对模型调优的例子多,但创新的混合模型仍相对较少,可尝试创新更多的混合预测模型来提高精度和效率。
(3) 网络安全态势的评估和预测缺乏通用的权重和定义标准,应考虑构建详尽的通用标准。
(4) 网络安全态势预测着眼于大规模网络,由于通常情况下网络的数据流量大、网络节点数量众多、网络环境复杂且异构,因此网络安全态势依然面临着难以预测的状况。
本文梳理近五年在NSSP领域的研究成果,分为不确定推理理论预测法、机器学习与人工智能方法、神经网络法三大类来介绍NSSP技术,对各预测模型的特性及优缺点进行阐述,并梳理时下热门的NSSP混合预测模型及优化模型以提高预测精度与效率,为研究人员和网络安全从业人员提供有效技术方案或优化策略参考,能够使研究人员对各预测方法有更深入的了解,对目前NSSP的发展和面临的挑战有更为详细的认识。

