基于实测材料参数的钢筋混凝土矩形柱偏心受压极限承载力计算研究
陈杰 陈顺超 聂良鹏 李正垣 邬文祥



摘 要:【目的】为了研究钢筋混凝土矩形柱在偏心受压情况下的极限承载能力。【方法】针对规范上已有的钢筋混凝土矩形截面偏心受压构件计算公式均以等效矩形应力分布图为基础的现象,本研究基于平截面假定,对混凝土压应力分布曲线进行积分并推导新的计算公式,通过MATLAB计算推导公式的理论值与钢筋混凝土矩形柱偏心受压构件试验所得的实测值进行比较。【结果】结果表明:钢筋混凝土矩形柱在偏心受压下,受拉区、受压区破坏现象与理论基本相符,通过推导的公式计算的极限承载力与实测值吻合程度较高。【结论】本研究验证了该推导公式可以对一般钢筋混凝土偏心受压情况下的极限承载力进行计算。
关键词:钢筋混凝土;矩形柱;偏心受压;极限承载力
中图分类号:TU375.3 文献标志码:A 文章编号:1003-5168(2023)09-0074-05
Abstract: [Purposes] To study the ultimate bearing capacity calculation of reinforced concrete rectangular columns under eccentric compression.[Methods] In view of the phenomenon that the existing formulas for calculating eccentrically compressed members with rectangular section of reinforced concrete in the specification are all based on the equivalent rectangular stress distribution map, this study integrates the distribution curve of concrete compressive stress and deduces a new calculation formula based on the assumption of flat section. The theoretical value of the formula calculated by MATLAB is compared with the measured value obtained from the experiment of the eccentrically compressed reinforced concrete rectangular column member. [Findings] The results show that the failure phenomena in the tensile and compression zones of RC rectangular columns under eccentric compression are basically consistent with the theory, and the ultimate bearing capacity calculated by the deduced formula is in good agreement with the measured values. [Conclusions] It is proved that the formula can be used to calculate the ultimate bearing capacity of reinforced concrete under eccentric compression.
Keywords: reinforced concrete; rectangular column; eccentric compression; ultimate bearing capacity
0 引言
作为建筑结构中占主导地位的钢筋混凝土结构被广泛应用于各种工程建筑中,其中偏心受压钢筋混凝土构件的使用在高层和桥梁建筑工程中应用广泛,如多层框架边柱、单层厂房排架柱、钢架柱、钢筋混凝土拱桥、隧道和桥墩桩等建筑结构中均有应用[1]。在设计偏心构件的过程中,为消除偏心受压构件承受弯矩和轴向压力而带来的安全隐患,极限承载力成为设计中最为重要的设计指标之一。极限承载力是钢筋混凝土构件受到极限荷载,并达到破坏状态时,其正截面的承载能力。西南交通大学张育智等[2]对影响钢筋混凝土偏心受压构件截面极限承载能力的因素(截面高度、截面宽度以及纵向钢筋面积)进行了分析研究。本研究对4根矩形截面钢筋混凝土柱进行偏心受压,对混凝土压应力分布曲线积分得到的推导公式计算的理论结果与实测结果之间的差异进行对比,通过分析差异的大小来论证推导公式是否可行。
1 试验方案
本次试验通过浇筑4根钢筋混凝土矩形长柱([5<Lh=9.58333≤30],其中L为试件计算长度;h為截面高度),且各个试件的初始偏心距分别为15 mm、45 mm、75 mm和105 mm,主要分析钢筋混凝土矩形截面柱在偏心受压下的极限承载能力及破坏行为的变化过程。经观察分析试验过程发现,矩形截面钢筋混凝土柱在加载到极限荷载时,其屈服行为与理论相符,即随着偏心距的不断增加,长柱的极限承载能力也会相应降低。
1.1 试验材料
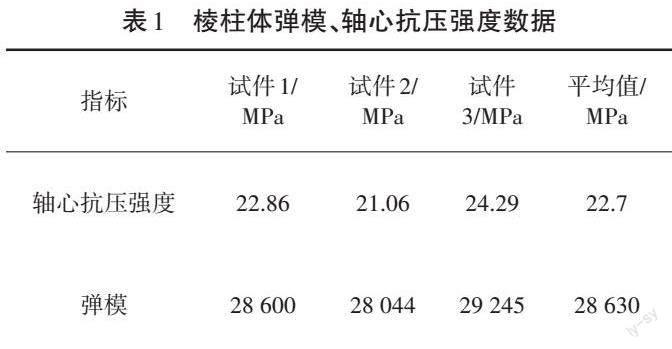
本试验中使用的混凝土强度等级为C25,受压主筋采用HRB400级钢筋,实测抗拉屈服强度为540 MPa,直径为8 mm,钢筋保护层厚度as=12 mm;箍筋采用HRB400级钢筋,实测抗拉屈服强度为540 MPa,直径为6 mm。为了保证使用的棱柱体弹模、强度数据均与钢筋混凝土构件一致,采用相同的材料和配合料的用量,制作3个棱柱体试件,在相同的条件下进行养护,并测定该棱柱体的弹模和轴心抗压强度,以供后期理论计算使用,棱柱体弹模等相关数据测量结果见表1。由表1可知,混凝土棱柱体的弹模可取29 000 MPa,轴心抗压强度可取平均值22.7 MPa。
表1 棱柱体弹模、轴心抗压强度数据
[指标 试件1/MPa 试件2/MPa 试件3/MPa 平均值/MPa 轴心抗压强度 22.86 21.06 24.29 22.7 弹模 28 600 28 044 29 245 28 630 ]
本试验主要用油压千斤顶进行测定,测定前须对50 t油压千斤顶进行数据标定,采用广州传感器,千斤顶的直径为108 mm, 面积为9 161 mm2。在标定过程中,分级加载进行标定,最终标定结果符合试验精度要求,可以用于偏压试验。
1.2 试验试样
本试验中,对4根钢筋混凝土矩形柱试件进行偏心加载试验,试验过程中要保证加载点和加载位置几何对中与物理对中。4个试件的横截面尺寸均为90 mm×120 mm(b=90 mm,h=120 mm),纵向钢筋的混凝土保护层厚度均设计为25 mm,矩形柱的高均设置为L0=1 150 mm。由于4根试件均为长柱,所以在试验中要考虑二阶效应对承载力的影响。试验所采用的试件均采用对称配筋,在受压侧和受拉侧均使用直径为8 mm的HRB400级的钢筋。
1.3 测试过程
本试验主要目的是测量钢筋混凝土矩形柱的极限承载能力,对比基于实测材料参数的钢筋混凝土矩形柱极限承载力理论计算值与其实测值吻合程度。试验中利用50 t油压千斤顶对试件进行偏心加载,在加载过程中,需分10级进行加载,每次加载稳定后维持3~5 min,记录相应数据。在正式加载前,先预加载1~2次,预载值要按理论计算值的10%计算。之后正常加载,每级荷载值也按理论计算值的10%计算。正常加载至理论计算值的90%时,此时每级的加载值需减少至理论计算值的5%,直到试件被加载至极限承载力且破坏为止,加载示意如图1所示。
2 公式推导
2.1 基本假定[3-5]
基本假定包括平截面假定、混凝土的抗拉强度忽略不计、钢筋的应力-应变曲线是已知的、混凝土受压的应力-应变曲线已知4个方面。钢筋的理想弹塑性应力-应变曲线如图2所示。《混凝土结构设计规范》(GB 50010—2002)[6]中,计算承载能力时所采用的混凝土受压应力-应变曲线,如图3所示。
2.3.2 对极限承载力N的求解。对钢筋混凝土矩形截面偏心受压柱的极限承载力进行求解计算,该求解过程由于需计算一元三次方程,计算比较烦琐,故应用MATLA编写计算程序对其求解。
3 试验结果分析
3.1 计算结果分析
通过计算流程编写的MATLAB程序[10-13]对推导公式进行计算, 4根试件的极限承载力计算结果与试验实测值见表2。
由表2数据分析可知,试件1、试件2和试件4
的理论计算值与试验所得的实测值吻合程度高达到94%以上,吻合程度较高;根据平截面假定可知,正截面承载力计算值与试验值的差异一般不超过10%,因此,柱1、柱2和柱4的试验实测值可以很好地论证根据曲线积分推导的公式准确性,该公式可以运用。然而试件3由于实测值偏低,导致吻合程度才达到73%。试验过后,对其实测值偏低进行了分析,主要原因是在试验过程中,试件3的加载点在摆放时出现了人为造成的操作误差,没能保证在截面的短边方向,从而导致试验的实测值偏低。
3.2 试验现象分析
试验过程中钢筋混凝土矩形柱的破坏过程如图5、图6所示(取一根试件在加载前与加载至破坏的过程为例)。
对试件试验全过程的破坏行为进行记录,在4组试验完全结束之后,观察分析4组试件,在开始受力后,试件的1/2范围左右均产生了较为明显的裂缝,裂缝均由试件底部开始出现,逐渐向上发展,直至试件破坏,其裂缝出现的先后次序都与理论相符合:试件在偏心加载过程中,最初的开裂只出现在受拉区,起初出现的裂缝宽度在0.14 mm范围内;后期试件在受拉区域的1/4、1/2和3/4处,裂缝逐渐伸展朝向外侧,混凝土受压区最终压碎破坏。
当钢筋混凝土试件受压较大一侧出现纵向裂缝时,试件将被压碎破坏,发生受压破坏现象。反之,试件另一侧受力较小,不论在受拉或者受压情况下,钢筋的应力都不能达到其屈服强度,但这种现象在偏心距较小的试件中,就没有表现得那么明显:受压破坏可能发生在受压较小的一侧,而且钢筋的屈服强度也能达到,甚至在发生破坏时,脆性破坏也可能会突然发生,并且受压一侧的钢筋的应力也能达到受压屈服强度。通过试验结果也可知:受拉钢筋的破坏主要是由于受拉钢筋首先达到屈服,破坏前横向裂缝有明显的延展,一条主裂缝形成,进而降低了屈服后钢筋受压区的高度,最终导致纵向裂缝出现在受压区且混凝土被压碎。
通过试验还发现,偏心受压试件在随着施加荷载逐渐增大的情况下,试件的受拉一侧将会出现明显的横向裂缝,而且与试件的纵向轴线垂直,但这种现象在试件偏心距很小的情况下不会出现。因此,试件的偏心距大小,直接关系到试件开裂时的荷载大小:如果试件的裂缝出现比较早,可以判断此试件为偏心距较大的试件;相反,如果试件的裂缝较晚出现,该试件的偏心距较小。
4 结论
综合以上基于实测参数并通过推导公式计算的极限承载力值与实测值以及试验现象对比分析,可得出以下结论。
①偏心加载的钢筋混凝土试件的破坏源于受压区的裂解失效且长柱在偏心受压下,需考虑二阶效应,而且在小偏心阶段二阶效应表现较为明显。
②观察试验现象可知,在其他条件相同的情况下,只从裂缝出现的时间上,就可以直接判断试件的偏心距的相对大小。
③根据混凝土受压的应力-应变曲线推导出的公式,通过MATLAB计算,在基于实测参数求解出的极限承载力与试验实测出的极限承载力吻合程度较高。
④本研究是基于我国规范进行的试验理论研究,可进一步综合对比其他国家的规范,对偏心受压构件正截面承载力的计算结果进行对比研究,以得出更为全面严谨的研究结论。
参考文献:
[1]杜虹茜. HRB600钢筋混凝土偏心受压柱受力性能试验研究[D].天津:河北工业大学,2018.
[2]张育智,何伟.钢筋混凝土偏心受压构件截面极限承载力影响因素研究[J].四川建筑科学研究,2011,37(6):70-74.
[3]赵国藩.高等钢筋混凝土结构学[M].北京:机械工业出版社,2005.
[4]朱剑锋.钢筋混凝土偏心受压构件计算商榷[J].甘肃科技,2007(7):142-144.
[5]陆艺诗.关于偏心受压构件承载力计算方法的比较研究[J].工程建设,2018,50(11):26-31.
[6]中华人民共和国住房和城乡建设部.混凝土结构设计规范:GB 50010—2002 [S].北京:中国建筑工业出版社,2002.
[7]仲伟秋,谢丽媛,董爱平.水下混凝土短柱正截面承载力计算[J].低温建筑技术,2011,33(1):39-42.
[8]彭飞,薛伟辰.FRP筋混凝土偏压柱承载力计算方法[J].建筑结构学报,2018,39(10):147-155.
[9]中华人民共和国交通运输部.公路钢筋混凝土及预应力混凝土桥涵设计规范:JTG 3362—2018 [S].北京:人民交通出版社,2018.
[10] 王萃敏,王兴国,苏幼坡,等.基于MATLAB语言的钢筋混凝土梁截面M-ϕ曲线[J].河北理工大学学报(自然科学版),2010,32(1):69-73.
[11] 范小春,熊立峰,王平.玄武岩筋混杂钢纤维混凝土短柱偏压试验与理论计算[J].硅酸盐通报,2020,39(10):3161-3168.
[12] 方恬.钢筋混凝土偏心受压构件正截面承载力的迭代计算法[J].苏州科技学院学报(工程技术版),2005(3):15-18.
[13] 张海涛,罗昊冲.对称配筋钢筋混凝土偏心受压构件的計算研究[J].中外公路,2017,37(4):126-130.

