基于主成分分析的温室内水面蒸发量估算模型构建及验证

王科，李银坤，郑文刚，刘美英，武佳乐，纪玉如，陈菲，侯升林

基于主成分分析的温室内水面蒸发量估算模型构建及验证

王科1, 2，李银坤1，郑文刚1，刘美英2*，武佳乐1, 2，纪玉如3，陈菲1，侯升林4

（1.北京市农林科学院 智能装备技术研究中心，北京 100097；2.内蒙古农业大学 草原与资源环境学院 内蒙古自治区土壤质量与养分资源重点实验室，呼和浩特 010018；3.中国农业大学 园艺学院，北京 100094；4.河北省农林科学院，石家庄 050051）

【目的】估算温室无风环境下的水面蒸发量（p）。【方法】基于温室内2020年与2022年3—7月的实测水面蒸发量（p）与气象数据，采用主成分分析法对p的影响因素进行分析，利用提取出的主成分与p构建多元回归模型，并对估算结果进行验证。【结果】试验期间p随试验时间的延长呈上升趋势，2020年3月与2022年3月的p日平均值分别为1.84 mm与1.94 mm，6月分别增加至3.77 mm与5.15 mm；辐射、湿度对温室无风环境下水面蒸发量的影响占主要地位，其中光合有效辐射与水面蒸发量的相关性最高，相关系数为0.852（＜0.01），其次为太阳辐射与湿度，相关系数分别为0.811与-0.770（＜0.01）。第一主成分的太阳辐射、光合有效辐射以及湿度对水面蒸发量影响较大，特征值为4.44，其中太阳辐射对水面蒸发量影响最明显，得分系数最高，为0.328；湿度与光合有效辐射次之，得分系数分别为0.311与-0.321。基于主成分分析结果建立了水面蒸发量估算模型，水面蒸发量估算值与实测值显著正相关（＜0.01），方程相关系数2为0.908，为0.10，为0.48 mm/d，一致性指数较高（=0.94）。【结论】在温室无风环境下太阳辐射、光合有效辐射与湿度对水面蒸发量影响较高。

温室；水面蒸发量；气象要素；多重共线性；主成分分析

0 引 言

【研究意义】我国设施蔬菜种植面积已达410 hm2，总产值占蔬菜产业的50%[1]。灌溉水是温室蔬菜水分需求的主要来源，灌溉决策不合理是我国目前盲目灌溉现象依旧普遍存在的主要原因[2]，灌溉量不足或过多不仅影响了蔬菜正常生产、浪费水资源，还导致了温室蔬菜经济效益下降等问题[3]。水面蒸发量是指单位时间内从单位（水）表面面积蒸发的水量，常表示为单位时间内从全部（水）面积上所蒸发的液态水的深度[4]，精确获取温室内水面蒸发量信息，对构建科学合理灌溉制度，促进温室蔬菜高产优质生产至关重要[5]。20 cm标准蒸发皿是目前直接测量不同生产条件下水面蒸发量（p）的主要方式，但人工测量的误差大、效率低，而采用自动称质量法的条件要求高、测量成本高[6]。模型估算法也是获取p的主要途径，该方法需要根据区域气候特点进行p模型构建与验证，具有应用范围广、成本低等优点[7]。建立适宜的p估算模型，对制定科学合理的灌溉制度、发展节水农业等具有十分重要的意义[2]。【研究进展】目前，p估算模型主要包括经验公式模型与机理公式模型。机理公式模型结构通常较为复杂，不利于推广应用，有研究[9]提出了气-水二维湍流流动理论模型，模型考虑了风在经过水体而产生的环流，以及空气流速、水温、气温等物理因素对水面蒸发的影响。经验公式模型包括2类，一类是考虑太阳、水与空气之间质量和能量的交换过程来估算p，例如Penman法[9]与波文比法[8]；另一类是以风速、水汽压差等其他气象因子建立的经验公式，例如Blaney-Criddle公式[7]。闵骞[8]对彭曼模型中的水面辐射平衡值与水面附近的空气干燥力2个参数进行修正，针对露天环境建立了以风速、湿度和饱和水汽压为主要参数的适用于全国的p模型。也有研究[10]以Blaney-Criddle公式为基础，建立了精度在月、旬、日的p经验模型，且p模型精度较原始模型有所提高；濮培民[11]通过分析水面蒸发过程中的水汽界面上的质量和能量传递过程，建立了基于温度、水汽压差、风速、相对湿度等因子的p估算模型。Jafari等[12]利用主成分回归法，建立了基于风速、湿度、水汽压差等气象因子的p估算模型，且精度明显高于回归模型；陆云燕等[13]利用主成分分析法，从诸多气象因子之间提取出3个主成分作为变量，与其建立的PCA-BP神经网络算法模型精度较高。【切入点】精确获取水面蒸发量是温室内水资源高效利用与农业灌溉制度确定的关键前提[14]。目前，p估算模型的研究主要针对露天环境，并将风速作为主要模型参数，但对温室无风环境下的p模型估算研究较少。【拟解决的关键问题】为此，本研究利用标准蒸发皿获取实测p，分析其在温室内无风环境下的主要变化趋势，利用主成分分析法探究影响p的主要因素，分析提取出的主成分与p的关系，进而建立基于主成分的温室内水面蒸发量估算模型并验证，为温室节水灌溉和绿色生产提供科学理论支持。

1 试验与方法

1.1 试验区概况

试验于2020年与2022年的3—7月在北京市农林科学院三连跨多功能连栋温室开展。试验温室南北走向，长39 m、宽11 m，试验布置于三连跨多功能连栋温室的中跨。试验温室位于东经116.29°，北纬39.94°，海拔56 m，多年平均气温为11.1 ℃，年均降水量为500～600 mm。该区属典型的温带大陆性季风气候。温室内透光性良好，且温室内气流较弱，风速近似为0。

试验期间种植作物为茄子，2020年3月1日定植，2020年7月15日收获，2022年3月3日定植，2022年7月15日收获。依据直径20 cm蒸发皿测定的水面蒸发量的80%进行灌水[15]，灌水周期为7～10 d。供试茄子品种为“京茄黑宝”，采用畦栽模式，栽培畦宽0.75 m，高0.1 m，每畦种植2行，株距为0.45 m，行距为0.5 m，试验区基施有机肥30 000 kg/hm2，试验期间追施水溶性肥料（（N）∶（P2O5）∶（K2O）=3∶1∶6）3次，每次纯氮施量为75 kg/hm2。

1.2 数据处理与分析

采用Excel 2016软件整理分析数据，利用SPSS 20.0对气象数据进行主成分分析，再将主成分与水面蒸发量进行多元回归分析。同时采用均方根误差（）、平均偏差（）与一致性指数（）等指标对估算值和实测值的符合度进行统计学分析。误差越小，越接近0，一致性指标越大，则模拟效果越好。

1.3 数据的选取与监测

利用2020年3月1日—7月15日实测逐日水面蒸发量与气象数据探讨温室内水面蒸发量变化规律及影响因素，并建立模型；使用2022年3月2日—7月15日的数据对模型进行准确性检验。

1.3.1 水面蒸发量

利用直径为20 cm的称质量式标准蒸发皿测定水面蒸发量（p），蒸发皿位于温室中央，精度为0.1 mm，每10 min测量1次数据。

1.3.2 气象数据

气象数据来源于温室内小型气象站（型号AG1000，美国生产），气象站位于温室中央，监测要素包括平均气温（）、日最高/低气温（max/min）、太阳辐射（a）、光合有效辐射（）和相对湿度（），数据采集间隔为10 min。通过FAO-56推荐方法计算饱和水汽压差（）[16]。

1.4 研究方法

1.4.1 多重共线性分析

“多重共线性”最早于1934年提出[17]，是指线性回归模型中的2个或多个变量之间，存在高度相关关系。共线性的存在会使回归模型剔除有用的自变量，导致模型失真或难以准确估计；或会使回归模型的系数符号与实际情况相反，使得模型中的变量无法得到合理的解释。

诊断多重共线性时，最常用的方法为方差膨胀因子法（）法[18]，在多元回归中，设有个自变量1，2，…，X，则：

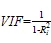
R2为X自变量与其他-1个自变量间的复相关系数。=1，则表明自变量X与其他-1个自变量之间没有共线性关系，一般情况下认为[19]，当≥10时自变量之间存在较为严重的共线性，且值越大，共线性越强。

还有研究[17]对的倒数，即容忍值（）法对回归模型的共线性进行进一步探讨：

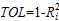
的取值在0～1之间，一般认为该值越接近0，说明自变量之间的共线性越强。

1.4.2 主成分回归

主成分回归是Massy[20]于1965年提出的一种解决多重共线性问题的新方法。基本思路是将原来多个自变量通过线性组合，转化为少数几个主成分，然后再将主成分与因变量建立回归方程，依据主成分与自变量的关系，求得基于原自变量的回归模型。

1.4.3 主成分分析

主成分分析[19]是通过降维将多个变量转化为几个互不相关的变量，其数学模型为：

对于个观测变量1，…，X，个观测的样本数矩阵：

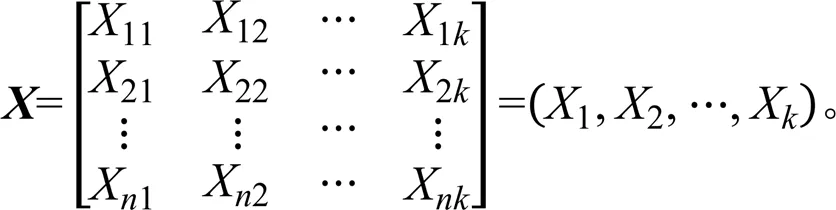
将个预测变量综合成为个新变量（综合变量），即：

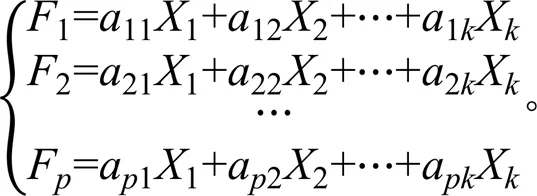
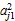
选取主成分的个数取决主成分的累计方差贡献率，通常选取累计贡献率大于85%以上等主成分，这些主成分更好地保留了原来因子的信息，减少了因子数量，从而起到筛选因子的作用。

1.4.4 多元回归分析

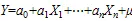
2 结果与分析

2.1 试验期间水面蒸发量变化规律

图1为2020年与2022年试验期间水面蒸发量（p）的逐日变化规律。温室内p年内变化规律一致，2020年和2022年温室内p的变化范围分别为0.19～6.85 mm和0.37～7.01 mm，p均值分别为3.32 mm和3.27 mm。随着试验时间的延长p呈波动上升趋势，2020年和2022年3月的p均值分别为1.84 mm和1.94 mm，6月p分别增加至3.77 mm和5.15 mm。

图1 温室内水面蒸发量动态

2.2 水面蒸发量影响因子筛选及影响因子间共线性诊断

表1为水面蒸发量（p）与气象因子相关分析结果。由表1可知，各气象因子均与水面蒸发量极显著相关（＜0.01），其中，与其负相关，其他环境因子均与p正相关。p与的相关性最高，相关系数为0.852，与min相关性最低，相关系数为0.428。

表1 温室蒸发皿水面蒸发量与气象因子的相关分析

注 **表示表示在0.01水平上显著相关。

由表1还可以看出，各气象因子之间存在明显相关性。其中，与a相关性最高，相关系数为0.968；而min与a、相关性均不显著。表2为采用方差膨胀因子法与容忍值法对各气象要素的共线性定量分析结果，可以看出，除外，各气象因子的容忍值均小于0.1，膨胀系数大于10，说明除以外的气象因子之间均存在较为严重的共线性问题，需要对数据进行主成分分析以解决共线性问题。

表2 共线性诊断

2.3 水面蒸发量主成分多元回归模型建立

对水面蒸发量影响的气象因子进行主成分分析表明，提取出2个主成分（1和2），1综合了原始变量的63.4%的变异信息，明显高于第二主成分2的24.5%，二者合计贡献率大于85%。这表明2个主成分在包含全部变量的同时，对水面蒸发量（p）的影响最为明显。依据表3各主成分的得分系数可知，1中a、和的载荷较大，得分系数分别为0.328、0.311和-0.321；2中与min的载荷较大，得分系数分别为0.353和0.431。故p主要受a、、、min的正向影响，受的负向影响。

依据表3提取出的2个互相独立的主成分1与2，与实测p进行多元回归分析，详见表4，建立的主成分回归模型参数均通过=0.05水平的显著性检验；模型决定系数2为0.854，表明p变化的85.4%是由1和2所代表的影响因子所引起的。

表3 主成分系数和贡献率

表4 水面蒸发量主成分多元回归模型

注 **表示表示在0.01水平上显著相关。

2.4 水面蒸发量估算值与实测值比较及相关性分析

将验证数据进行标准正态变换后，代入表4主成分回归模型中，水面蒸发量（p）估算值与实测值变化趋势如图2所示，估算值与实测值全生育期变化规律一致，峰值较为接近，分别为6.88 mm和7.01 mm。整个生育期的p估算值为441.16 mm，与实测p相比，高估了14.82 mm。p的实测值与估算值相关性如图3所示，模型估算值与实测值极显著正相关，方程决定系数2为0.908（＜0.01），回归趋势线与1∶1线较为接近，可见模型估算值与实测值有较高的线性相关。

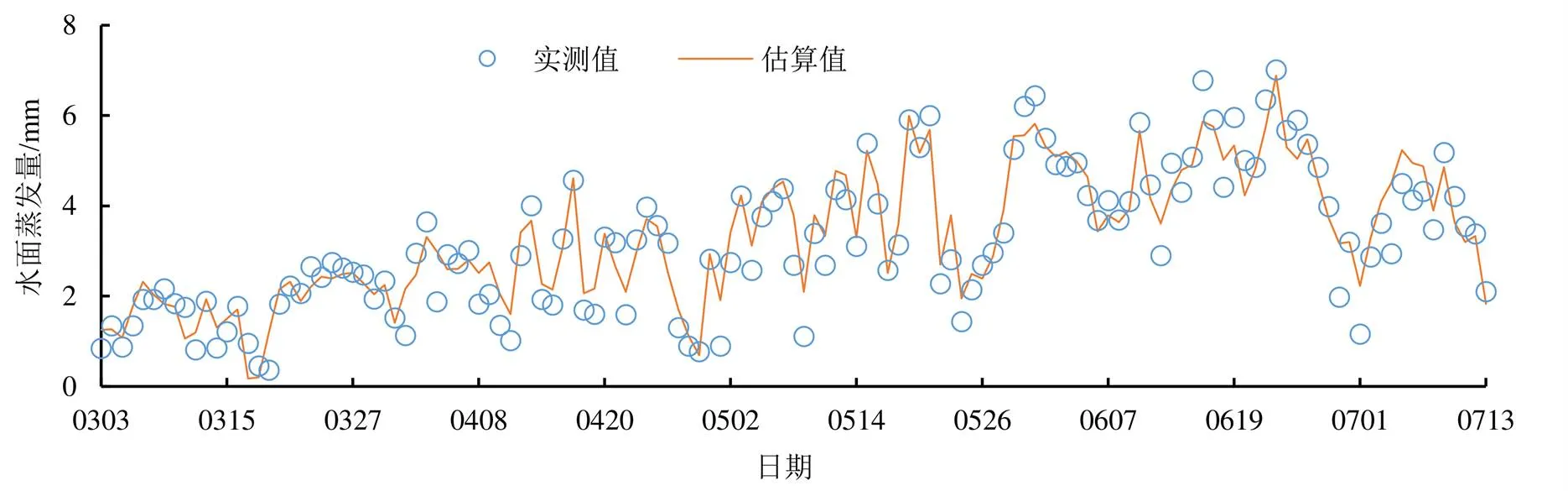
图2 水面蒸发量估算值与实测值比较

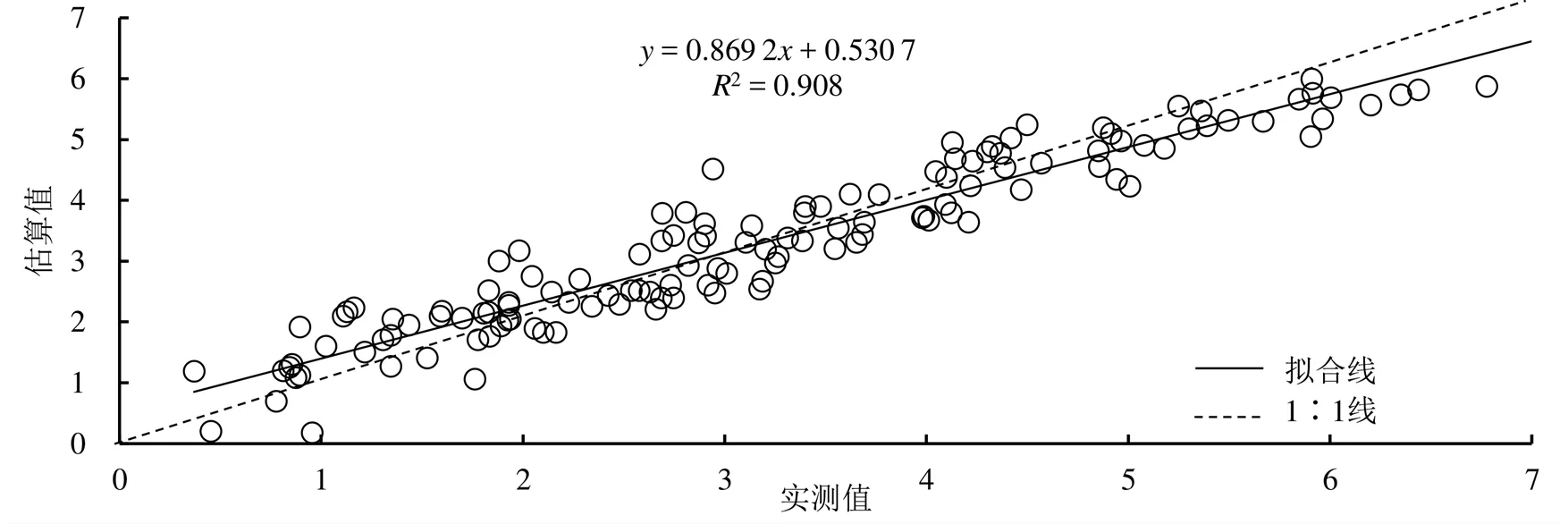
图3 水面蒸发量估算值与实测值相关性比较

2.5 水面蒸发量估算值与实测值的统计分析

为进一步评价水面蒸发量（p）估算模型的估算精度，对模型的估算值与实测值进行统计分析，详见表5。基于模型估算的日均p为3.32 mm/d，与实测p相对误差为3.51%，为0.48 mm/d，为0.10，一致性指数为0.94，综合来看模型误差较低。

表5 模型估算值与蒸发皿实测水面蒸发量比较的统计特征值

注 比值为日均估算水面蒸发量与日均实测水面蒸发量之比，为一致性指数。

3 讨 论

本试验中，水面蒸发量（p）整体呈波动上升趋势，这与环境温度不断上升，光照逐渐增强等有关[8]。陆云燕等[13]研究表明，露天环境下的p从4—7月呈逐渐升高趋势。水面蒸发主要因为水面水汽压大于上空水汽压，而使逸出水面的水分子多于大气返回的水分子量，其蒸发强度与气象因子相关性较高，且受各气象因子影响程度不同[21]。本研究表明，p与a的相关系数为0.811，与的相关系数为0.852（＜0.01），明显高于p与的相关系数0.751，p与的相关系数-0.770（＜0.01）。这与李银坤等[2]在温室环境中的研究结果类似。但露天环境条件下，与是影响p的主要环境因素[8]。这可能是露天环境中风速较强而造成的研究结果差异。孙凤贤等[22]、刘昌宇[9]对静止水面下p的主要影响因素的研究得出，在风速较低时，太阳辐射强度越高，p越大，且在无风环境下，光照强度对p的影响可以提高21倍。本研究中主成分分析的结果也进一步说明了这个问题，对p影响最大第一主成分的主要影响因素为a、和，主成分贡献率可达63.4%；而第二主成分的主要影响因素为和min，主成分贡献率仅为24.5%。可见，温室环境条件下a与对p的影响，明显强于与对p的影响。

多元回归模型中，多重共线性问题的来源主要是自变量自身的性质，即多个自变量之间高度相关[17]。本研究中，除外，各气象因子之间容忍值皆小于0.1，膨胀系数大于10，这说明除以外的气象因子之间存在较为严重的共线性[19]，而共线性强的各气象因子之间通常存在较为紧密的联系。如表1所示，a与显著负相关（＜0.01），相关系数可达-0.773，而与其他气象因子显著正相关（＜0.01），相关系数在0.4以上。这主要是因为环境中热量的主要来源是太阳辐射，随着光照增强，温度升高，饱和水汽压差也随之升高，空气随着温度的升高而膨胀，因此单位体积内的水分子减少，湿度随之降低[21]。许莹莹等[19]研究发现，平均气温、地温、绝对湿度和水汽压差间彼此密切相关，相关系数在0.75～0.97之间，共线性分析表明，地温、绝对湿度和平均气温的容忍度均小于0.1，方差膨胀因子均大于10，说明各影响因子之间存在较为严重的共线性。可见各自变量之间联系较为紧密时，会在建立回归方程时产生共线性问题。本研究利用主成分回归法建立的p估算模型的相对误差为3.51%，值为0.48 mm/d，一致性指数为0.94。主成分分析可以很好地解决共线性问题，具有降低模型误差的效果[17]。Jafari[12]研究发现，使用主成分回归模型来预测p的模型2为0.82，为0.52 mm/d，而多元回归模型的2为0.79，为2.28 mm/d。还有学者[17]利用了主成分分析与相关分析相结合的方式，重新提取出7个各自独立的变量，消除了传统最小二乘法建立的多元回归模型中存在的共线性，并利用多元回归分析建立了模型。陆云燕等[13]使用机器学习算法的建模方式，将提取出的主成分，通过BP神经网络建立p的估算模型，得到了较好的结果。本试验利用不同年份数据，建立了基于主成分分析的p估算模型，为估算温室环境下的p提供了可靠的依据。

4 结 论

1）温室2020年与2022年春茬茄子种植期间水面蒸发量（p）的变化范围分别为0.19～6.85 mm和0.37～7.01 mm，且随试验时间的延长，p呈上升趋势。

2）温室无风环境内，辐射因素与湿度对p的影响占主导地位，其中与p的相关性最高，相关系数为0.852（＜0.01），与a、的相关系数分别为0.811和-0.770（＜0.01）；在主成分分析中得出，1对p影响最明显，特征值最大，为4.44，其主要代表a、和对p的影响，各因子得分系数分别为0.328、0.311和-0.321。

3）建立了基于主成分分析的多元回归p估算模型，该模型消除了各变量之间的共线性，其估算值与实测值显著正相关（＜0.01），2为0.908，为0.10，为0.48 mm/d，一致性指数较高（=0.94），模型估算误差较低。

[1] 周杰, 夏晓剑, 胡璋健, 等. “十三五”我国设施蔬菜生产和科技进展及其展望[J]. 中国蔬菜, 2021(10): 20-34.

ZHOU Jie, XIA Xiaojian, HU Zhangjian, et al. Technological development and production of protected vegetable in China during’The thirteenth five-year plan’ and future prospect[J]. China Vegetables, 2021(10): 20-34.

[2] 李银坤, 詹保成, 郭文忠, 等. 基于蒸发皿水面蒸发量的温室生菜适宜灌溉量研究[J]. 灌溉排水学报, 2022, 41(4): 13-19.

LI Yinkun, ZHAN Baocheng, GUO Wenzhong, et al. Optimizing irrigation amount for greenhouse lettuce production based on pan-measured evaporation[J]. Journal of Irrigation and Drainage, 2022, 41(4): 13-19.

[3] LIU H, DUAN A W, LI F S, et al. Drip irrigation scheduling for tomato grown in solar greenhouse based on pan evaporation in North China plain[J]. Journal of Integrative Agriculture, 2013, 12(3): 520-531.

[4] 段莉珠. 障碍物遮挡率对水面蒸发量的影响浅析[J]. 黑龙江水利科技, 2019, 47(9): 75-77.

DUAN Lizhu. Preliminary analysis of influence of barrier shielding ratio on evaporation quantity of water surface[J]. Heilongjiang Hydraulic Science and Technology, 2019, 47(9): 75-77.

[5] 郭文忠, 陈青云, 高丽红, 等. 设施蔬菜生产节水灌溉制度研究现状及发展趋势[J]. 农业工程学报, 2005, 21(S2): 24-27.

GUO Wenzhong, CHEN Qingyun, GAO Lihong, et al. Present situation and developmental tendency on system of water-saving irrigation of vegetable production in protective cultivation[J]. Transactions of the Chinese Society of Agricultural Engineering, 2005, 21(S2): 24-27.

[6] 周书影. TEZ-601全自动称重式蒸发系统在杜陵水文站的应用比测分析[J]. 广东水利水电, 2020(12): 50-53.

ZHOU Shuying. Application research of TEZ-601 automatic weighing evaporation system in duling hydrology station[J]. Guangdong Water Resources and Hydropower, 2020(12): 50-53.

[7] 武金慧, 李占斌. 水面蒸发研究进展与展望[J]. 水利与建筑工程学报, 2007, 5(3): 46-50.

WU Jinhui, LI Zhanbin. Advances and prospect of research on water surface evaporation[J]. Journal of Water Resources and Architectural Engineering, 2007, 5(3): 46-50.

[8] 闵骞. 利用彭曼公式预测水面蒸发量[J]. 水利水电科技进展, 2001, 21(1): 37-39.

MIN Qian. Prediction of water surface evaporation by penman formula[J]. Advances in Science and Technology of Water Resources, 2001, 21(1): 37-39.

[9] 刘昌宇. 太阳光谱吸收对静止水体蒸发影响的研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.

LIU Changyu. Effect of spectral absorption of solar energy on evaporation of still water[D]. Harbin: Harbin Engineering University, 2014.

[10] 闵骞. 湖泊(水库)水面蒸发量预测方法的探讨[J]. 水文, 1997, 17(2): 39-43

MIN Qian. Discussion on prediction method of lake (reservoir) water surface evaporation[J]. Hydrology, 1997, 17(2): 39-43.

[11] 濮培民. 水面蒸发与散热系数公式研究(一)[J]. 湖泊科学, 1994, 6(1): 1-12.

PU Peimin. Studies on the formulae for calculating evaporation and heat loss coefficient from water surface in China(I)[J]. Journal of Lake Science, 1994, 6(1): 1-12.

[12] JAFARI Majid, DINPASHOH Y. Derivation of regression models for pan evaporation estimation[J]. Environmental Resources Research, 2019, 7(1): 30-42.

[13] 陆云燕, 王振龙, 吕海深, 等. 基于主成分分析和BP神经网络的五道沟水面蒸发计算研究[J]. 水文, 2022, 42(1): 35-39.

LU Yunyan, WANG Zhenlong, LYU Haishen, et al. Calculation of water surface evaporation in Wudaogou based on principal component analysis and BP neural network[J]. Journal of China Hydrology, 2022, 42(1): 35-39.

[14] 刘海军, 黄冠华, 王明强, 等. 基于蒸发皿水面蒸发量制定冬小麦喷灌计划[J]. 农业工程学报, 2010, 26(1): 11-17.

LIU Haijun, HUANG Guanhua, WANG Mingqiang, et al. Sprinkler irrigation scheme of winter wheat based on water surface evaporation of a 20 cm standard pan[J]. Transactions of the Chinese Society of Agricultural Engineering, 2010, 26(1): 11-17.

[15] 王湛, 李银坤, 郭文忠, 等. 不同灌水量对温室茄子蒸腾规律及水分利用的影响[J]. 中国农村水利水电, 2019(7): 6-10.

WANG Zhan, LI Yinkun, GUO Wenzhong, et al. The effect of different irrigation amount on the transpiration rate and water use efficiency of autumn eggplant in greenhouses[J]. China Rural Water and Hydropower, 2019(7): 6-10.

[16] 胡晨, 葛继稳, 许向南, 等. 基于FAO56 Penman-Monteith公式估算神农架大九湖泥炭湿地蒸散及作物系数[J]. 应用生态学报, 2020, 31(5): 1 699-1 706.

HU Chen, GE Jiwen, XU Xiangnan, et al. Estimation of evapotranspiration and crop coefficient in Dajiuhu peatland of Shennongjia based on FAO56 Penman-Monteith[J]. Chinese Journal of Applied Ecology, 2020, 31(5): 1 699-1 706.

[17] 杨梅, 肖静, 蔡辉. 多元分析中的多重共线性及其处理方法[J]. 中国卫生统计, 2012, 29(4): 620-624.

YANG Mei, XIAO Jing, CAI Hui. Multiple collinearity in multivariate analysis and its processing methods[J]. Chinese Journal of Health Statistics, 2012, 29(4): 620-624.

[18] 梁素梅, 吴迪. 基于多重共线性的气象观测站优化模型[J]. 价值工程, 2020, 39(32): 157-160.

LIANG Sumei, WU Di. Optimization model of meteorological observation station based on multicollinearity[J]. Value Engineering, 2020, 39(32): 157-160.

[19] 许莹莹, 李薇, 王振龙, 等. 基于主成分分析的裸地潜水蒸发与气象要素关系模拟[J]. 水文, 2020, 40(4): 7-13, 39.

XU Yingying, LI Wei, WANG Zhenlong, et al. Simulation of relationship between evaporation and meteorological elements of bare ground diving based on principal component analysis[J]. Journal of China Hydrology, 2020, 40(4): 7-13, 39.

[20] MASSY W F. Principal components regression in exploratory statistical research[J]. Journal of the American Statistical Association, 1965, 60(309): 234-256.

[21] 李万义. 适用于全国范围的水面蒸发量计算模型的研究[J]. 水文, 2000, 20(4): 13-17, 63.

LI Wanyi. A study on the generalized model of water surface evaporation[J]. Hydrology, 2000, 20(4): 13-17, 63.

[22] 孙凤贤, 刘昌宇, 夏新林, 等. 太阳辐照对静止水面稳态蒸发的影响[J]. 计算物理, 2014, 31(6): 699-705.

SUN Fengxian, LIU Changyu, XIA Xinlin, et al. Effect of solar radiation on evaporation of still water surface[J]. Chinese Journal of Computational Physics, 2014, 31(6): 699-705.

Construction and Validation of a Model for Estimating Surface Water Evaporation in Greenhouse Based on Principal Component Analysis

WANG Ke1,2, LI Yinkun1, ZHENG Wengang1, LIU Meiying2*, WU Jiale1,2, JI Yuru3, CHEN Fei1,HOU Shenglin4

(1. Intelligent Equipment Research Center, Beijing Academy of Agriculture and Forestry Sciences, Beijing 100097, China;2. Inner Mongolia Key Laboratory of Soil Quality and Nutrient Resource, College of Grassland, Resources and Environment, Inner Mongolia Agricultural University, Hohhot 010018, China;3.College of Horticulture, China Agricultural University,Beijing 100094, China; 4.Hebei Academy of Agriculture and Forestry Sciences, Shijiazhuang 050051, China)

【Objective】Surface water evaporation (p) in greenhouse is often used as a reference in irrigation management. The purpose of this paper is to present a model to estimate it.【Method】The model was derived based on meteorological data and pan-evaporation measured from March to July in 2020 and 2022. The relationship betweenpand meteorological data was analyzed using the principal component method, from which a multiple linear regression model was developed to estimatep. 【Result】pincreased as time elapsed, with its average increasing from the range of 1.84～1.94 mm in March to the range of 3.77～5.15 mm in June in both 2020 and 2022.pwas influenced by radiation and relative humidity the most.Photosynthetically active radiation had the highest correlation withp, with their correlation coefficient being 0.852 (<0.01), followed by solar radiation and relative humidity with their associated correlation coefficient being 0.811 and -0.770, respectively (<0.01). The first principal component of solar radiation, photosynthetically active radiation, and relative humidity has a great effect onp, with the eigenvalue being 4.44. The solar radiation affectedpsignificantly, with the highest score coefficient (0.328), followed by relative humidity and photosynthetically active radiation, whose score coefficients were 0.311 and -0.321, respectively.Principal component analysis and verification showed that the estimatedpusing the proposed model agreed well with measured data, with<0.01,2=0.908,=0.10,=0.48 mm/d, and the consistency index=0.94.【Conclusion】Solar radiation, photosynthetically active radiation, and relative humidity are the main factors influencingpin the greenhouse. The multiple linear regression model derived from the principal component analysis is accurate and can provide real-time estimates of surface water evaporation in the greenhouse.

greenhouse; pan evaporation; meteorological factors; multiple collinearity; principal component analysis

王科, 李银坤,郑文刚, 等. 基于主成分分析的温室内水面蒸发量估算模型构建及验证[J]. 灌溉排水学报, 2023, 42(5): 60-66.

WANG Ke, LI Yinkun, ZHENG Wengang, et al.Construction and Validation of a Model for Estimating Surface Water Evaporation in Greenhouse Based on Principal Component Analysis[J]. Journal of Irrigation and Drainage,2023, 42(5): 60-66.

1672 - 3317（2023）05 - 0060 - 07

P332.2

A

10.13522/j.cnki.ggps.2022543

2022-09-30

河北省重点研发计划项目（21327005D）；国家重点研发计划项目政府间国际科技创新合作专项（2019YFE0125100）；河北省现代农业产业技术体系项目（HBCT2021200201，HBCT2021200202）

王科（1999-），男。硕士研究生，主要从事作物水肥高效利用研究。E-mail: wke1020@163.com

刘美英（1974-），女，内蒙古清水河人。副教授，硕士生导师，主要从事土壤肥力与植物营养方面的教学科研工作。E-mail: liumeiyingimau@163.com

责任编辑：白芳芳