基于变权TOPSIS模型的围岩质量评价方法研究*

王凤山 钱 津

（陆军工程大学野战工程学院 南京 210007）

1 引言

围岩作为支撑地下结构荷载的主要成分，其质量评价是工程界研究的热点问题［1］。围岩受岩体结构面、受力状态、地应力环境及开挖扰动等因素影响，易引起塌方、岩爆、涌水等工程灾害，有效把握围岩自然属性与工程特性，科学提取和分析围岩质量评价指标，是围岩质量评价的关键事项。

辨析围岩变形与破坏的衍化机理和致灾过程，是解析围岩质量评价所要解决的核心节点问题［2］，全面考察影响围岩稳定性的多重要素，以期把握围岩质量评价中的模糊性、随机性特征。以弥补常权决策的偏差为目标，变权TOPSIS 模型强调因素权重与因素状态值的联系、演变特征。集合TOPSIS［3］方法应用于围岩质量评价，寻求基于正、负理想方案间的一致和妥协，以期提高决策结果的科学有效性。

2 围岩质量影响因素概述

围岩有着稳定性的系统，但其同时还具有开放性，根据位置和时间的不同而变化，遵循地表、地下等外力作用下围岩地质体系统物质、能量和信息的交互机制和平衡作用，适应量化评估围岩质量仿真推演的需要，从系统化角度建立影响围岩质量的结构、要素、介质的规范化描述［4］，实现了影响围岩质量要素及指标提取的一致性语义表达，如图1所示。

图1 影响围岩质量要素描述

图1中，围岩质量评价要素在结构上反映评价模型的本质思想和关键概念，是考察围岩质量整体作用体系的重要工具［5］。围岩稳定性受岩体质量、完整程度、地壳外力等多种内外因素的影响，对围岩质量评价要素的辨识和集合设计，目的是构建围岩质量评价模型的指标体系，为质量评价模型和系统分析建立基础，参考文献资料和行业规范［6］，选取6 个因素作为围岩稳定性评价的指标，分别为岩石抗压强度（单轴）K1、岩石质量指标K2、岩体完整性系数K3、地下水发育状态K4、岩体声波速度K5以及结构面走向与洞轴线夹角K6，建立指标体系集合，K={K1，K2，……Kn}，(1≤n≤6)。

3 指标权重计算

3.1 熵值法计算指标权重

熵值法［7］以原始信息作为数据支撑，是一种度量无序程度的客观赋权方法。其中心思想是通过监测各项指标的变异程度来测算出指标熵值的大小：熵值越大，反映出该指标信息的不确定性越大，包含的信息越小；反之，熵值越小，则该指标信息的稳定性越好，相应包含的信息越大。

1）设对m种方案si(1≤i≤m)构成围岩质量方案集合S={si|1≤i≤m} 进行对比评价，结合n项指标属性构成m×n原始数据矩阵，记作Smn={sij}m×n，即为

式（1）中，i表示评价方案数量，j表示指标属性个数，sij为第i个方案第j个指标值。

2）采取极差法对围岩质量评估原始数据矩阵Smn进行标准化处理。结合式（2）、式（3）计算标准化矩阵S'。

围岩质量指标呈现效益型特征时：

围岩质量指标呈现成本型特征时：

3）根据熵值计算方法（4），围岩质量第i个要素指标下Si的熵值为

式（4）中pui表示围岩质量第i项指标下，第m个标段的特征比重，则：

式（4）中，zi表示围岩质量各指标要素的信息熵值，熵值越大，表示出围岩质量指标体系的整体稳定性越差，权重越小。至此，计算围岩质量评估指标的权重αi为

式（6）中，0≤αi≤1，

3.2 变异系数法计算指标权重

传统熵值法仅依赖于数据本身的离散性，在测算权重时出现有的权重过大或过小的情况，对应指标数据为0 和1 时算出熵值均为0，很容易会造成关键信息的丢失。变异系数［8］是衡量方案中各个属性值变异程度大小的统计值，变异系数法［9］则是通过计算各属性在被评价对象上变异程度而得到权重的客观赋值方法。

第一步：对第j个被评价属性参数值求取均值和标准差σj：

第二步：计算第j个属性指标的变异程度γj：

第三步：计算出各项指标的权重βj，通过对相应指标的变异程度进行“归一化”处理：

3.3 均值化计算指标权重

考虑不同单一赋权法间偏差值较大，利用熵值法和变异系数法分别确定围岩评价权重{αj}、{βj}（1≤j≤n），虽然消除了方案属性量纲的差异，但也消除了各指标变异程度上的差异，因此，通过引入均值思想［10］对指标权重进行平衡处理，具体如下：

式（10）中，ωj=a·αj+(1-a)βj，本文取a=0.5。

4 变权TOPSIS评价模型

TOPSIS 法［11］又叫逼近理想解的排序法，是经典的多属性决策方法。其中心思想在于：对方案进行评价时，首先计算出最佳方案和最差方案，即：评价问题的理想解和负理想解，然后利用欧式距离计算法求出各指标对象与正理想解和负理想解之间的贴近程度，进而通过与理想解的相对贴近度对方案进行排序和评价，若评价对象距离正理想解最近且距离负理想解最远，则为最佳方案，反之最差［8］。

但TOPSIS 方法［12］所采取的指标权重基本上是由专家主观确定的，其客观准确度较低。因此运用均值化方法组合计算信息熵和变异系数法的指标权值，取代了以专家经验主观上确定权重的方法，同时根据TOPSIS 法结合各指标属性的评价值［13］，对最终的目标方案进行整体评价。

1）建立目标方案评价模型的决策矩阵并进行相应的标准化处理，得到矩阵S，如式（11）。

2）根据确定的各评价指标权重系数，构建加权标准决策矩阵U，如式（12）。

3）确定正理想值U+和负理想值U-，计算正、负理想值，如式（13）、（14）。

式（13）、（14）中，J+为效益型评价指标集，J-为成本型评价指标集。

4）求任一解yij到正负理想解的距离Li+、Li-，如式（15）、（16）。

式（15）、（16）中，u+、u-分别表示正负理想解的第j个分量。

5）计算各方案到理想解的贴近度Gi。

式（17）中，0≤Gi≤1，i=1，2，…，m。

6）根据相对贴近度Gi对各个方案进行排序，选择贴近度最大的方案为较优方案。

5 模型计算

5.1 标准化决策矩阵

以地下洞室内典型区域为例，根据文献［11］对4 个标段内围岩稳定性指标为例，给出围岩稳定性样本s1、s2、s3、s4的相关特征指标取值，构建地下洞室结构的围岩稳定性质量评价样本集，其量化参数如表1。

表1 围岩稳定性质量评价样本集

建立方案决策矩阵Y，利用式（11）对矩阵Y进行规范化处理，则标准化矩阵S表示如下：

5.2 计算指标权重

根据公式计算熵值法、变异系数法、均值化法下的指标权重，具体如表2所示。

表2 围岩质量评价指标权重

表2中，分别表示出三种方法下的指标权重α、β、ω，并以此为数据支撑进行各方案正、负理想解求解。

5.3 求解各方案正、负理想解

依据式（13）～（14）依次求得各方案正、负理想解，如表3所示。

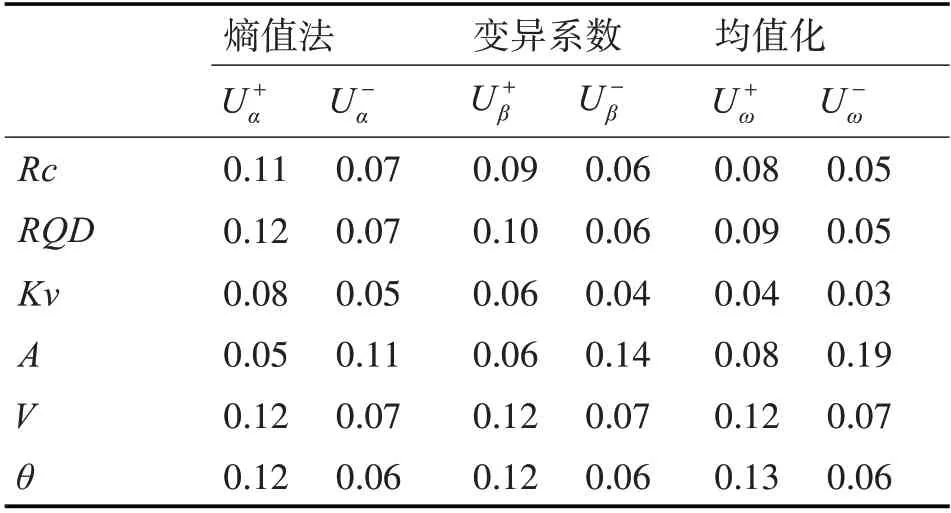
表3 围岩质量评价方案正、负理想解

5.4 计算到正负理想解的距离

依据式（15）～（16）依次求得各方案到正、负理想解的距离，如表4所示。

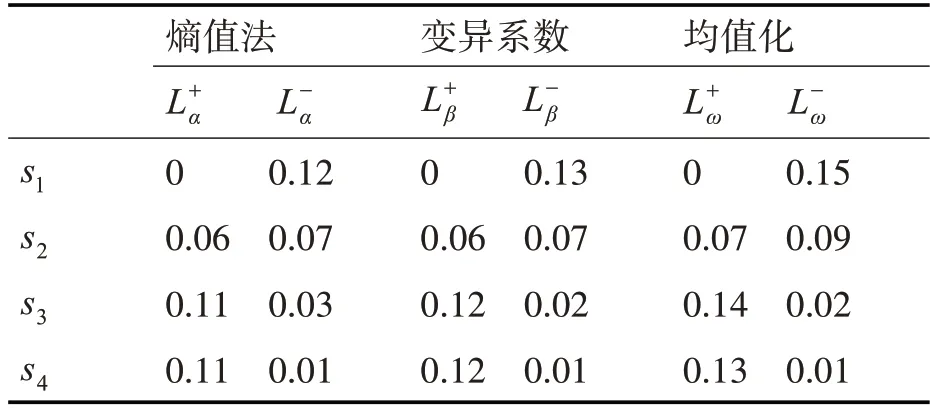
表4 评价方案到正、负理想解的距离

5.5 计算相对贴近度并排序

根据式（17）依次求得各方案的相对贴近度G，如表5所示。

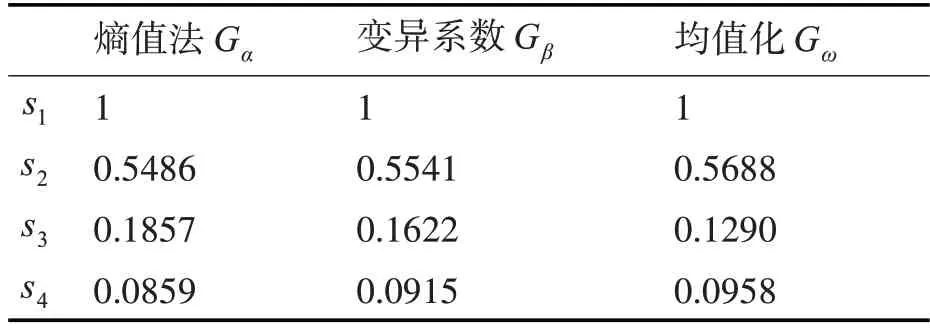
表5 围岩质量评价方案贴近度

5.6 模型效果分析

根据表5对围岩质量评价方案贴近度进行排序，熵值法、变异系数法与均值化下的方案贴近度排序一致，结果为s1＞s2＞s3＞s4。数据显示，均值化作用后的围岩质量评价方案中，方案s2的贴近度高于常权作用下的方案贴近度，且方案s3、s4的贴近度更接近，对比工程实测数据更符合实际。通过贴近度大小排序可以清晰得出方案s1的围岩质量最好、稳定性最高，对比工程实测结果一致，表明基于变权TOPSIS的围岩质量评价模型计算结果可靠，准确性较高，具有较好的应用价值。

6 结语

1）针对围岩质量评价的多指标性，从系统化的角度提取影响围岩质量的各种因素，选取围岩单轴抗压强度、岩石质量指标、岩石完整性系数、地下水发育状态、岩体声波速度、结构面走向与洞轴线夹角作为评价指标，构建围岩质量评价模型［11］。

2）在评价过程中，采用熵值法、变异系数法对评价指标进行均值化赋值，克服了单一赋权法中指标差异度较大、敏感性较强等特征对围岩质量评价结果的影响，增强了围岩质量评价模型的科学性、安全性。

3）以工程实例为数据支撑进行仿真计算，在围岩现地指标测算值和方法算出组合权重值的基础上，计算理性点贴近度与实例工程数据对比，结果表明基于变权TOPSIS的围岩质量评价模型得出的结论与实际结果一致，表明该方法、模型的合理可行。