显式结构拓扑优化方法在声子晶体中的应用研究*

张亚茹 郭 辉 孙玲莉 汪熙婷 程 乾

（上海工程技术大学机械与汽车工程学院 上海 201620）

1 引言

声子晶体由人工复合材料周期性排布而成，具有独特的阻挡某一特殊频段波传播的能力［1～5］。这一特殊频段称之为带隙。带隙特性与组成声子晶体的材料参数，结构几何尺寸和元胞拓扑有密不可分的关系。为了最大程度挖掘带隙特性，科研人员开展了一系列声子晶体拓扑优化研究［6～10］。

目前关于声子晶体元胞拓扑优化的研究工作主要集中于离散像素单元策略，即将声子晶体元胞离散成为N*N 个像素单元，通过优化算法（遗传算法［6～7］，双向进化结构演化算法［8］等）确定各像素单元的材料属性，进而确定元胞拓扑结构。在像素型结构优化工作中，易出现以下几个问题：1）优化过程中易出现棋盘格模式和孤岛现象，导致优化过程失稳或优化结构不具备实际意义；2）像素单元尺寸过大导致优化结构边界粗糙，单元尺寸过小则会显著降低优化效率，且微观结构不易制备；3）基于离散单元策略的优化结构，因其隐式参数特性，无法直接获取声子晶体元胞拓扑参数，难以在CAD 软件中建模和分析。

为了解决上述问题，本文开展了基于可移动形变组件法［11～14］的声子晶体显式结构拓扑优化研究。基于若干个可自由移动伸缩变化的组件，组成元胞拓扑，以实现利用构件几何位置倾角参数显式表征元胞拓扑参数的目的。将元胞拓扑转化为数值表达后，结合移动渐近线法对构件几何位置参数进行优化。针对面内模式和面外模式，开展了元胞拓扑优化工作。显式表征结构拓扑，有利于声子晶体建模分析以及加工制备，对于促进声子晶体的工程应用具有一定的意义和价值。

2 优化模型的建立

2.1 能带结构的计算

当弹性波在均质板中传播时，其波动方程如下所示：

式中，ρ为介质密度，u为位移向量，λ和μ是材料拉梅常数，r是位置矢量。

由于结构的周期性，结构位移可以用以下公式来描述：

其中k是布洛赫波矢，为便于计算其在第一布里渊区的取值，uk(r)是具有与结构同等周期的位移函数。

采用有限元法进行能带结构计算，对于任意离散单元可以得到如下动力学方程：

其中，是结构全局刚度矩阵，是结构全局质量矩阵，u是结构位移幅值矩阵。

将布洛赫波矢k绕不可约布里渊区边界扫掠，则可以得到各布洛赫波矢下对应的结构共振频率，即得到能带结构图。

2.2 可移动形变组件法

可移动形变组件法中元胞拓扑结构将由以下公式确定：

其中φs(x)是构件的拓扑描述方程，D为结构的设计域，Ωs为结构内部，∂Ωs为结构内部边界。其中，φs(x)=max(φ1(x)，…，φn(x))，φi(x)为第i 个构件的拓扑描述方程。拓扑描述函数是利用水平集算法的思想，用数个关键的参数来表达构件拓扑形状的函数。在本文中，构件的拓扑描述函数为

其中，x0和y0为构件中心点的坐标，L 和t 为构件的宽度和高度，θ为构件的轴线与水平线的夹角。m 是一个自定义参数，在本文中m 值为6。在本文中，采用矩形构件建模，于是采用可移动形变组件法来实现声子晶体带隙优化可以被表示为

其中，di代表第i 个设计变量di=[xi，yi，Li，ti，θi]，g(d) 为结构优化过程中用来约束设计的约束函数。在这篇论文中，采用四节点等参单元来离散声子晶体元胞结构。在优化过程中，构件的结合信息作为设计变量一直在变化，不断的更新网格将会使构造全局矩阵的过程变得更加复杂。因此，采用固定网格法［14］来划分结构。对于任意一个单元，只要它的四个节点的拓扑描述值是已知的，则这个单元的弹性模量可以被插值为

其中，E 为材料的弹性模量，H 为heaviside 函数，φei为这个单元四个节点上的拓扑描述值，q为常数，在本文中取2。为了缩小误差以使H函数具有实际意义，H函数为以下公式：

ε是控制归一化幅值的参数，α是一个极小的数值，来确保整体刚度矩阵的非奇异性。建立了有限元分析模型之后，采用移动渐近线法［16］进行设计变量数值优化运算。为了便于移动渐近线法的使用，目标函数可以被等效替换为

于是，目标函数对于各个设计变量的灵敏度则为

其中：

其中位移矩阵已经经过归一化处理。经过上述计算后，则可得到各设计变量的灵敏度，结合移动渐近线法，即可实现声子晶体元胞显式拓扑优化。

3 结果与讨论

在本文中，使用铅和硅橡胶来设计声子晶体拓扑结构，具体材料参数如表1 所示。在利用可移动形变组件法进行元胞拓扑显式优化中，合理选择初始结构对于优化效果及优化效率具有一定的影响。在优化初始阶段，建立如下图所示的网状拓扑超材料。

表1 材料参数属性

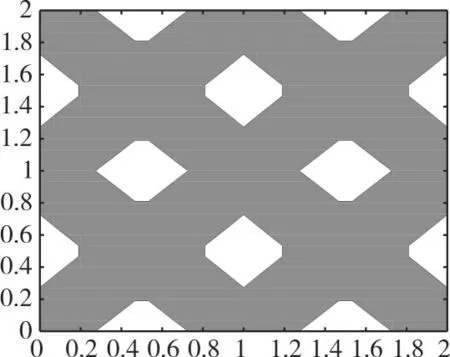
图1 初始元胞拓扑

在面内模式下，由于高对称点Γ 的存在，导致结构不可能在第一能带和第二能带之间打开带隙。为此，在面内模式下，拓扑优化的目标函设置为第三带隙相对带宽：

面外模式下优化目标函数设置为：

经优化后，可得到如下图所示的最优结构及其能带结构图。从最优结构中可以看出，经对称展开后，该元胞结构中间部分存在一个“日”字形的由铅组成的散射体，其中左右两侧较粗，上下两侧较细，并且结构中心部分存在一个较小的硅橡胶孔洞。从其能带结构图中可以看出，该结构能够在373.3Hz～807.1Hz 处打开带隙，相对带宽为73.5%。由于z 向振动的特殊性，结构能在第一能带和第二能带之间打开带隙。从结构图中可以看出，所有构件都聚集在设计域的一角。绘制该结构的能带结构图，可以看出，该结构在392.74Hz～1643.5Hz处具有带隙，其相对带宽122.8%。

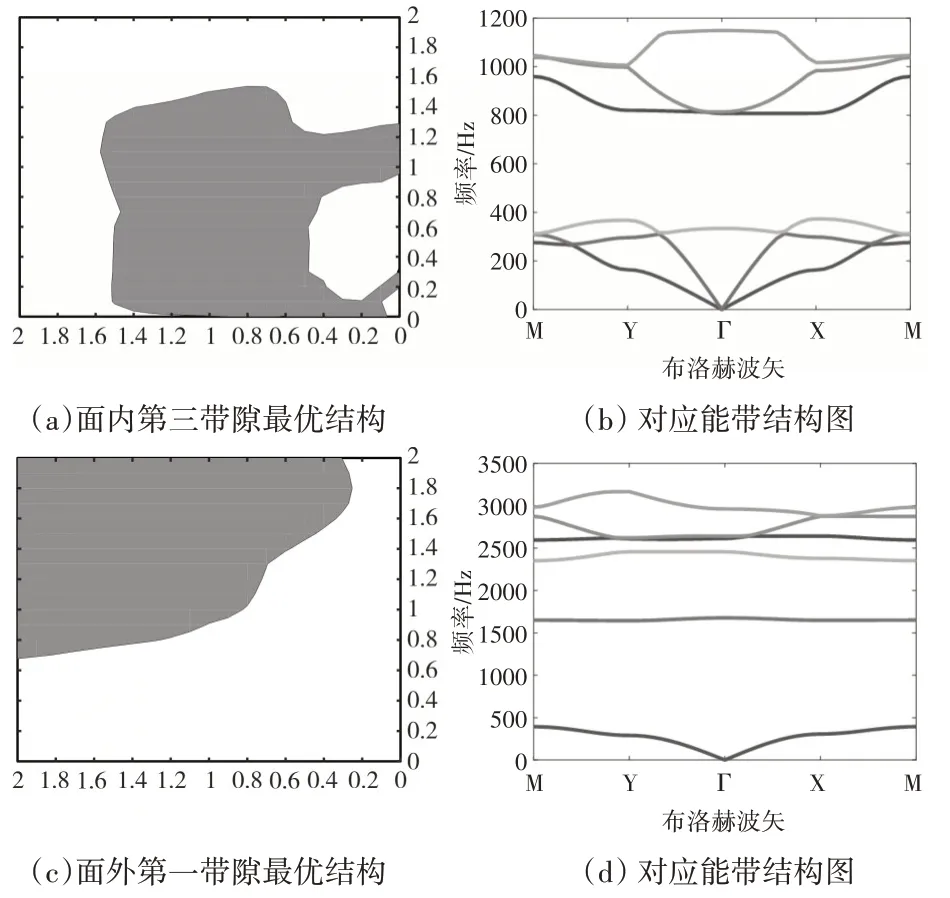
图2 优化结构及其对应能带结构图

为了验证可移动形变组件法优化的有效性，针对面内模式第三带隙优化结构构建传输特性损耗模型。具体模型如图3所示。

图3 传输特性损耗模型

针对面内模态最优结构模型，在结构左侧施加机理，并在模型右侧提取加速度值，根据两者比值绘制传输特性谱，所得传输特性曲线谱如图4所示。

图4 传输特性曲线谱

从图4 中可以看出，传输特性谱在对应的带隙区间内有明显的下降趋势，即表明结构在对应的频段处具有良好的弹性波衰减能力，验证了优化方法的有效性。

4 结语

本文采用可移动形变组件法，开展了声子晶体元胞拓扑优化工作。相比于遗传算法，双向进化结构优化算法等优化算法，基于灵敏度分析策略的可移动形变组件法能大幅提高优化效率，且优化效果良好。针对声子晶体元胞面内模态第三带隙和面外模式第一带隙开展优化工作，分别获得了373.3Hz～807.1Hz 和392.74Hz～1643.5Hz 的带隙，其相对带宽值分别为73.5%和122.8%。相比于其他优化算法，可移动形变组件法具有优化效率高，显式拓扑参数，便于建模和分析等优点，具有良好的理论意义和工程应用价值。