带直角等六边形钢管混凝土柱的局压性能

王志滨，戴鸿伟，汪炳坤，李栋

（福州大学 土木工程学院，福建 福州 350108）

钢管混凝土因施工方便、承载力高、延性好等优点，受到工程界重视，已在桥梁结构和大跨度结构中被大量运用［1］.但是常见的圆形和矩形截面已满足不了人们对建筑外形及受力性能等各方面的需求，因此有工程师提出了带直角等六边形钢管混凝土柱，该类柱子可用作建筑物的角柱，如天津高银大厦和北京中国尊大厦等.同时桥梁结构也常采用带直角的六边形墩柱.

实际工程中，桥梁结构和大跨度结构的墩柱常处于局压状态，构件的局压承载力一般低于其全截面受压承载力.刘威等［2-4］研究了圆形和矩形钢管混凝土柱的局压性能，发现：圆形截面组合柱的局压承载力高于方形截面组合柱；端板刚度越大，组合柱的局压承载力越高.刘劲等［5］完成了12 个圆钢管混凝土短柱的局压试验，并通过拟合有限元参数分析结果提出该类组合柱局压承载力的计算公式.Han 等［6］报道了36 个钢管约束混凝土局压试验，发现钢管混凝土的承载力和局压面积比成反比.Yang 等［7］基于22 个矩形钢管混凝土柱的局压试验，发现该类试件的延性随着局压面积比和端板厚度的增大而提高.沈奇罕等［8］采用有限元模型研究圆端形钢管混凝土试件的局压性能，最终提出了该类组合柱的局压承载力设计方法.

对于带直角等六边形钢管混凝土柱：Xu 等［9］发现，该类组合柱的约束作用主要集中在角部；对于轴压或纯弯构件，随着含钢率的增大，局部屈曲的现象会得到改善，其混凝土可以采用同截面的矩形钢管约束混凝土本构模型来模拟.吴泓均等［10］采用有限元法研究该类组合构件在双向偏压荷载下的力学性能，发现该类组合构件的弯矩相关曲线在小轴压比时呈1/4 圆，在高轴压比时呈1/4 椭圆.王志斌等［11］采用有限元法分析该类组合柱的压弯滞回性能，发现该类组合柱绕强轴破坏时展现出更好的延性.此外，该作者［12］还通过限元分析发现，和同截面面积的方钢管混凝土柱相比，带直角等六边形钢管混凝土柱展现出更强的耐火性能.

综上，现有局压研究多集中于传统的圆形（或矩形）钢管混凝土柱，尚未开展带直角等六边形钢管混凝土柱的研究，但该类构件有可能承受局压荷载.因此本文加工了20 个带直角等六边形钢管混凝土柱并开展了局压试验；建立该类组合柱的仿真模型，基于该模型开展该类组合柱在局压荷载下的工作机理和参数影响分析；提出了该类组合柱的成套局压设计理论.

1 试验研究

1.1 试验概况

本文加工了20 个带直角等六边形钢管混凝土试件（截面如图1所示，B为钢管边长，D1和D2分别代表截面高度和宽度，mm，ε11、ε1t分别代表纵向、横向应变片），其中包括17个局压试件和3根全截面受压对比试件.垫块形状均为带直角等六边形，厚度均为40 mm.试验参数为局压面积比（β=Ac/AL，AL和Ac分别为局压面积和组合柱中混凝土截面面积，mm2）、端板厚度（ta，mm）和含钢率（α=As/Ac，As为组合柱的钢管截面面积，mm2）.

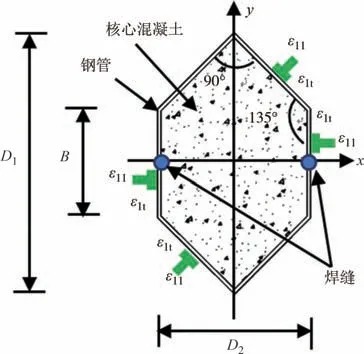
图1 构件截面Fig.1 Cross-section of specimens

试件尺寸见表1，表中L、b和t分别为试件长度、垫块边长和钢管厚度，fy和fcu分别代表实测钢管屈服强度和核心混凝土立方体抗压强度.试件编号中“LH”代表局压试件，“HCFT”代表对比试件；第一个数字6、10、14 分别代表含钢率为0.06、0.1 和0.14；第二个数字1.2、2、3、4 分别代表β为1.44、4、9 和16；第三个数字0、3、6、10、12 代表端板厚度；最后一个字母a、b代表两个相同试件.其中含钢率为0.1、局压面积比为4 的典型试件LH10-2-0 和LH10-2-6 各加工了2 个，其余试件则只加工1 个.表1 中KLC为相对承载力系数；Nue、NuFE和NuL分别代表实测承载力、有限元预测承载力及简化计算承载力，kN.

表1 试件和试验结果Tab.1 Details of specimens and measured result

试件加工采用如下流程：1）首先将钢板弯折成两个V 形角钢；2）将两个V 形角钢焊接成带直角的等边钢管；3）将12 mm 厚的下端板与钢管焊接；4）浇筑部分混凝土并振捣密实，然后重复上述步骤，直到混凝土高出上端面；5）自然养护一周后，磨平上端面；6）最后在部分试件上焊接端板.

所有试验在500 t压力机上进行.如图2所示，通过试件上端面形心处的垫块施加局压荷载，4个位移计被用于测量竖向位移，在距离组合柱上端面1.9B、0.5L处的钢管外表面布置应变片，截面上的应变片测点如图1所示.

图2 试验装置Fig.2 Test setup

采用如下加载制度：先采用荷载加载，荷载增量为0.1NuFE，每级荷载持荷2 min；当加载至0.7NuFE时，采用位移慢速加载［13］.停止加载条件包括：1）焊缝开裂；2）承载力下降50%；3）垫块被完全压入混凝土中.

1.2 试验结果及分析

1.2.1 破坏模态

图3 给出了试件破坏模态示意图，对于无端板试件，上端面混凝土被挤压到相邻截面的混凝土中，使该截面的混凝土向外和向上膨胀，钢管向外屈曲，部分混凝土向上拱起，导致部分钢管有可能处于受拉状态.对于带端板试件，上端部混凝土被挤压到相邻截面的混凝土中，导致该截面的混凝土向外和向上膨胀，并将上端板拱起.由于受到上端板的限制，混凝土的侧向变形量更大，钢管屈曲现象更严重.图4 为试件整体破坏模态，在局压荷载作用下，距离加载端1.9B的截面均由六边形发展为椭圆形.

图3 破坏模态Fig.3 Failure model

图4 所有试件破坏模态Fig.4 Failure mode of all specimens

1.2.2 荷载（N）-位移（Δ）曲线

图5 所示为各参数对N-Δ曲线的影响.可见：试件的初始刚度和承载力随着局压面积比的减小而提高，但曲线的下降段更陡，试件表现出更好的延性，原因是局压面积比越大，混凝土承压面积越小，受到周围混凝土和钢管的约束作用越强，因此延性越好.试件的初始刚度和承载力随着端板厚度的增加而提高.原因是端板越厚，试件的整体性越好，越不容易发生混凝土局压破坏.试件的N-Δ曲线的下降段随着含钢率的增大而变缓，原因是含钢率越高，钢管约束效果越好.

图5 N-Δ曲线Fig.5 N-Δ curves

1.2.3 荷载（N）-应变（ε）曲线

图6 所示为各试件加载端的N-ε曲线，应变以受拉为正、以受压为负.其中横向实测应变均为拉应变，纵向实测应变均为压应变.端部截面的核心混凝土受压膨胀，导致钢管发展较大横向拉应变.

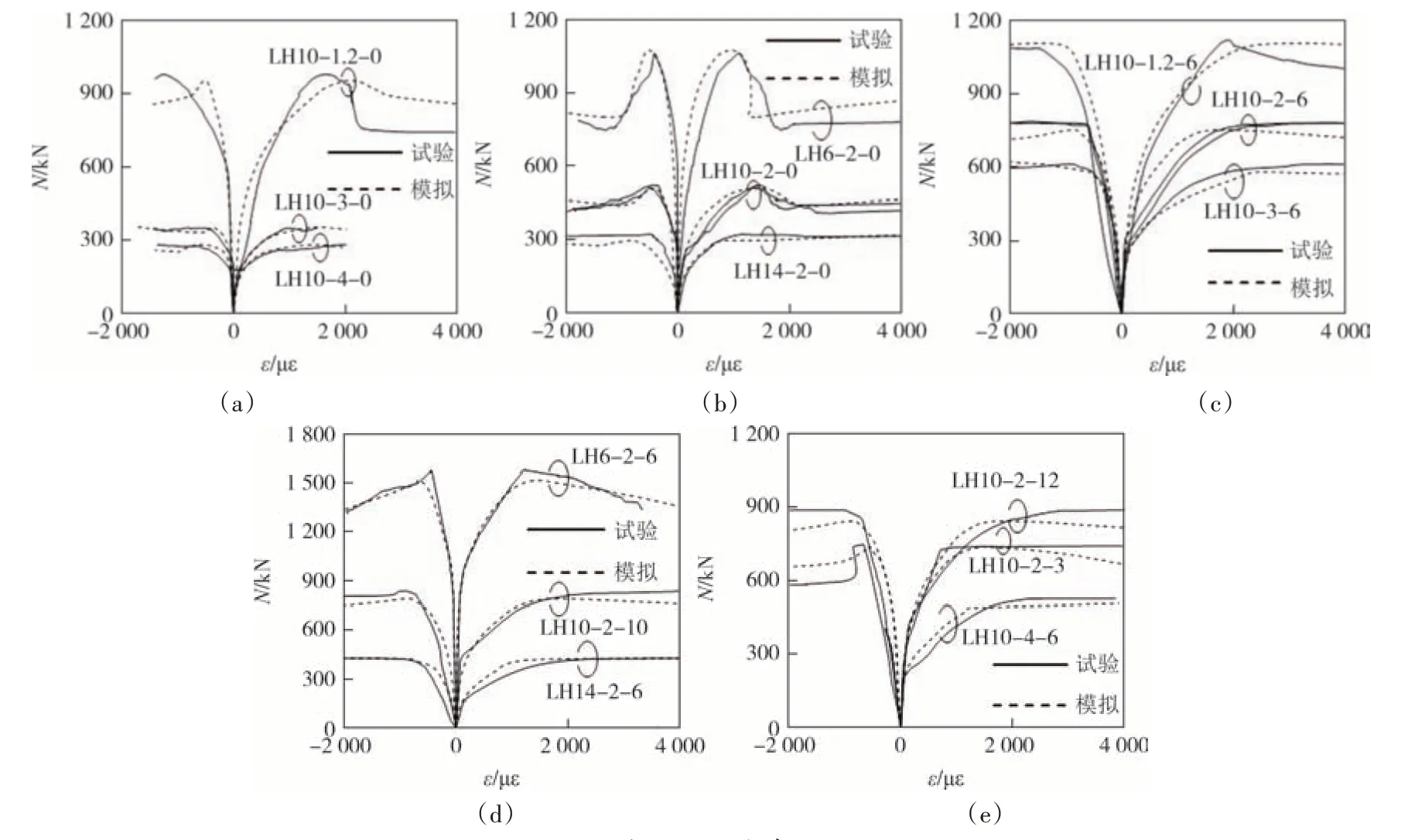
图6 N-ε曲线Fig.6 N-ε curves

1.2.4 相对承载力系数

为分析局压荷载对钢管混凝土柱承载力的影响，本文采用文献［14］定义的相对承载力系数（KLC）：

式中：NuL和Nu分别为钢管混凝土组合构件的局压承载力和该构件全截面受压时的承载力，kN.

图7 表示了各参数对KLC的影响规律.可发现：KLC随着局压面积比的增大而减小，但随着端板厚度的增大而增大.与全截面受压对比试件相比，局压面积比从1.44 增大到16，无端板试件的承载力下降了21.8%～79.3%，带端板试件的承载力下降了10.6%～63.2%；当端板厚度从0 mm（无端板情况下）增大到 3 mm 时，局压试件的KLC提升了46.2%，而端板厚度从3 mm 增大到12 mm 时，KLC仅提升19.2%，可见适当地增设端板可显著提高试件的局压承载力.对于无端板试件，KLC随着含钢率的提高而缓慢增大；对于带端板试件，含钢率对KLC的影响不大.

图7 各参数对实测KLC的影响Fig.7 Effects of parameters on measured KLC

2 仿真模拟

采用有限元软件ABAQUS进行仿真模拟.

2.1 材料模型

钢材采用Tao 等［15］提出的弹塑性模型.混凝土采用Tao 等［16］提出的矩形钢管混凝土模型，使用时按截面面积相等原则将六边形混凝土等效成其中一条边长为1.41B的矩形截面［9］.

2.2 模型建立

四对组件（钢管-核心混凝土、端板-核心混凝土、垫块-核心混凝土、垫块-端板）间的切向采用“库伦摩擦模型”，摩擦因数取为0.6，法向采用“硬接触”［13］.采用黏接（Tie）模拟端板和钢管间焊接关系.钢管采用S4 单元，端板、核心混凝土和垫块均采用C3D8R 单元.通过试算可确定合理的网格密度.图8所示为带直角等六边形钢管混凝土局压试件的有限元模型，限制试件底端所有节点的自由度，将局压垫块耦合（Coupling）在其上端面形心处的参考点1 上，然后在参考点1上施加纵向位移.

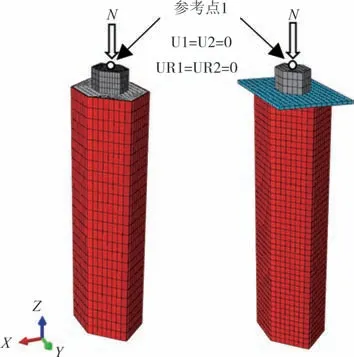
图8 有限元模型Fig.8 Finite element model

2.3 模型验证

从图3 和图4 可以看出该模型可模拟该类试件的端部钢管向外屈曲、端截面形状趋于椭圆和核心混凝土开裂.因局压破坏主要表现为端截面破坏，图6 提供了有限元模拟端截面处钢管纵向应变和横向应变曲线与实测曲线的对比.表1 提供了有限元模拟承载力（NuFE）与实测承载力（Nue）的对比，NuFE/Nue的平均值和标准差分别为1.029 和0.058.可见本文的有限元模型可很好地模拟该类试件的局压承载力和应变发展规律，可用于工作机理分析和参数影响分析.

3 工作机理分析

本文利用以上有限元模型对典型带直角等六边形钢管混凝土短柱进行局压工作机理分析，分析加载全过程组合柱及其各组件的纵向应力及接触应力的发展规律.典型试件基本参数如下：B=250 mm，L=1 436 mm（L≈5.8B），β=4，t=9.2 mm，fy=355 MPa，fcu=60 MPa，ta=0 mm或10 mm，α=0.1.

图9 为两种典型试件、钢管组件和混凝土组件的荷载（N）-轴向应变（ε）曲线.为方便比较，图中还给出了全截面受压对比试件的N-ε曲线.由图9 可知：峰值荷载作用时混凝土承担了超过90%的荷载.峰值荷载作用后，混凝土进入软化段，试件和混凝土的承载力开始下降，但是下降幅度不大，最后剩余承载力趋于平稳；和全截面受压对比试件相比，不带端板试件和带端板试件的承载力分别下降了64.3%和51.6%.

图9 典型试件的N-ε曲线Fig.9 N-ε curves of typical specimens

由图4 可知局压试件一般在距试件加载端1.9B的截面发生破坏.因此图10和图11着重分析典型试件在峰值荷载作用下该截面的纵向应力分布，图10及11 中fc'为混凝土圆柱体抗压强度，MPa.从图11中可看出混凝土纵向应力分布以垫块为核心向四周逐渐减小，在截面边缘甚至会出现微小的纵向拉应力，而该截面的钢管基本上处于受拉状态.原因是局压垫块被压入混凝土中，导致混凝土向四周膨胀，部分混凝土甚至向上膨胀，从而在混凝土和钢管的接触面上形成向上的摩擦力，使得部分钢管处于受拉状态.

图10 无端板试件端截面纵向应力分布Fig.10 Longitudinal stress distribution of end section of specimen without end plate

图11 带端板试件端截面纵向应力分布Fig.11 Longitudinal stress distribution of end section of specimen without end plate

图12 为两种典型试件在峰值荷载作用时，钢管4 个点所在棱线沿高度的横向拉应力分布图.可见，两种典型试件在距加载端0～1.2B的范围内发展了较大的横向拉应力，横向拉应力甚至超过fy，说明在该范围内钢管对核心混凝土形成较大约束；到加载端的距离超过1.2B时，钢管的横向拉应力迅速下降至0.1fy～0.2fy.

图12 沿构件高度的钢管横向应力分布Fig.12 Lateral stress distribution of steel tube at different heights of specimen

从图13可见钢管与混凝土接触应力（p）随试件轴向变形的发展情况，其中A、B、C三个特征点与图9的特征点一致，可发现：1）钢管的约束作用主要集中在转角处；2）小转角处（90°）钢管的约束力明显大于大转角处（135°）；3）无端板试件中钢管主要发挥约束作用，因此钢管转角处的约束力明显大于带端板试件.

图13 钢管与混凝土的接触应力Fig.13 Contact stress between steel tube and concrete

由图14 可见局压垫块形状对典型试件承载力的影响.可见无端板时当采用带直角等六边形垫块时，其局压承载力比采用方形和圆形垫块时承载力分别降低了15.2%和10.7%.但是，对带端板的带直角等六边形钢管混凝土柱，局压垫块形状对承载力影响很小，主要是因为端板起到类似于垫片的作用，使得试件顶部受力更均匀.

图14 垫块形状的影响Fig.14 Effects of cushion block shape

4 参数影响分析

本文基于以上模型对该类新型组合柱进行参数影响分析，主要考虑β、fcu、fy、α、端板刚度［（nr，由式（2）计算［3］）］和偏心率（e/B，其中e为荷载偏心距）等参数对带直角等六边形钢管混凝土试件局压性能的影响.典型算例的主要参数为B=250 mm，L=1 436 mm，β=4，t=9.2 mm，fy=355 MPa，fcu=60 MPa，α=0.1，ta=0 mm 或10 mm.考虑到带直角等六边形垫块加载为最不利情况，本文参数分析统一采用带直角等六边形垫块.

式中：Lk为钢管端板扰度的影响高度，Lk=1.914B；E=(Es⋅As+Ec⋅Ac)/AL，Ec为混凝土弹性模量，MPa；Es为碳素钢材的弹性模量，取20 600 MPa；AL=As+Ac.

钢管混凝土局压承载力（NuL）可由式（3）～（6）计算［1］：

式中：fck为混凝土抗压强度标准值，fck=0.67fcu.

由图15 可知：试件的KLC随着β的增大而减小.当β从1.44 增大到25 时，无端板试件的KLC下降了85.2%，带端板试件的KLC下降了62.1%.随着fcu的提高，KLC呈线性增大，当fcu从30 MPa 增加到120 MPa时，无端板试件的KLC增加了138.7%，带端板试件的KLC增加了96.6%.随着fy的增加，KLC呈现缓慢增大趋势，当fy从235 MPa增加到550 MPa时，无端板试件的KLC仅增加了20.9%，带端板试件的KLC仅增加了24.3%.α对KLC的影响较小，当α从0.05 增加到0.2时，无端板试件和带端板试件的KLC仅分别增加了2%和5%.同时可见，试件的KLC随着nr的增加而增加；e/B对KLC影响较小.

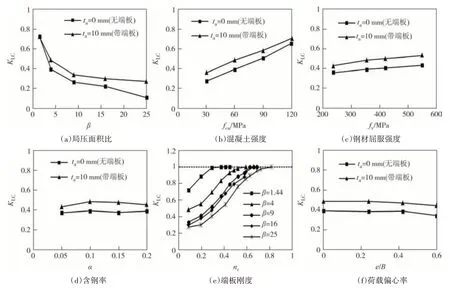
图15 各参数对KLC的影响Fig.15 Effects of parameters on KLC

5 实用设计理论

式（3）仍可用于预测钢管混凝土构件的局压承载力，但需建议新型组合柱的承载力折减系数（KLC）的实用计算方法.

5.1 无端板带直角等六边形钢管混凝土

对于无端板带直角等六边形钢管混凝土柱：

其中，

图16 给出了采用式（3）、式（7）计算的108 个典型有限元算例的局压承载力（NuL）和有限元预测承载力（NuFE）的比较，NuL/NuFE的平均值为0.935，标准差为0.076.图17 给出了NuL与实测值（Nue）的比较，NuL/Nue的平均值为1.002，标准差为0.055.可见以上公式具有较高的精度.

图16 简化计算值（NuL）与有限元值（NuFE）的比较Fig.16 Comparisons between NuL and NuFE

图17 简化计算值（NuL）与实测值（Nue）的比较Fig.17 Comparisons between NuL and Nue

5.2 带端板带直角等六边形钢管混凝土

对于带端板带直角等六边形钢管混凝土柱：

图16 给出了采用式（3）、式（8）计算的243 个典型有限元算例的NuL和NuFE的比较，NuL/NuFE的平均值为1.000，标准差为0.087.图17 给出了NuL与Nue的比较，NuL/Nue的平均值为0.87，标准差为0.08.可看出以上公式总体偏于保守.

6 结论

本文开展了带直角等六边形钢管混凝土柱的一系列局压试验和理论研究，得出如下结论：

1）试验表明，带直角等六边形钢管混凝土局压短柱的破坏模态表现为垫块下的混凝土发生局压破坏，四周混凝土向外膨胀，钢管向外屈曲，加载端面最终发展为椭圆形.试件的承载力和端板厚度呈正比，和局压面积比成反比；局压面积比越大试件延性越好.设置端板可有效提高试件的局压承载力.

2）机理分析表明，局压受力状态下，荷载主要由混凝土承担，六边形钢管的约束力主要集中在角部.对无端板试件，带直角等六边形垫块作用下是最不利的.两种典型试件在距加载端0～1.2B的范围内发展了较大横向拉应力，说明在该范围内钢管对核心混凝土形成较大约束；到加载端的距离超过1.2B时，钢管横向拉应力迅速下降至0.1fy～0.2fy.

3）参数分析表明，该类组合短柱的承载力随着局压面积比的增大而降低，但随着混凝土强度和端板厚度的增大而提高.含钢率、钢材屈服强度和偏心率对该类组合柱的局压承载力影响较小.

4）提出了该类新型组合短柱局压承载力的实用预测模型，简化计算承载力与数值模型预测值（或实测承载力）吻合较好，可为相关工程实践提供参考.