基于边界分析的刚果（金）某铜钴矿床氧化矿资源量估算

摘要：传统方法进行氧化矿资源量估算，一般采用工业品位圈定矿体并用矿体内数据进行估值。实践表明，传统圈矿方法会增强工业品位域内高品位数据的连续性，而导致显著的品位高估。边界分析通过考察特定地质域或品位域边界一定范围内的样品品位变化，对边界类型进行判断。硬边界条件下仅采用工业品位域内数据进行估值，而软边界条件下矿化域内数据也应参与资源量估算。实际案例研究结果表明，采用软边界条件进行建模和估值，考虑了样品数据在地质和统计上的连续性，估值准确度高，且不会遗漏工业矿体。该方法流程简单快捷，技术重复性强，应作为改进的资源量估算方法进一步推广应用。

关键词：距离幂次反比；分形分析；变异函数；硬边界；软边界；夹石；资源量估算

中图分类号：TD15 P618.14文献标志码：A开放科学（资源服务）标识码（OSID）：

文章编号：1001-1277（2023）03-0058-07doi：10.11792/hj20230313

引 言

刚果（金）铜钴成矿带是全球最重要的沉积层状铜矿带之一，刚果（金）也成为当前中国企业最重要的海外矿产开发基地之一。区域内铜钴矿床形成后遭受了不同程度的氧化富集作用。氧化矿体因厚度大、埋藏浅、品位高，以及适合露天开采和湿法冶炼工艺等而具有较高的经济价值。因此，准确估算氧化矿石资源量对于矿山设计和开发有重要的现实意义。根据GB/T 13908—2020 《固体矿产地质勘查规范总则》^［1］，不同工业矿石类型（如氧化矿、混合矿、硫化矿，工业矿、低品位矿）应单独圈矿并估算资源量。分别圈算矿量的问题在于：一方面资源量估算的工作量成倍增加，耗时过长；另一方面，单一矿石类型内的已知样品数据可能偏少，不论是样品数据的统计分析，还是基于已知样品数据的插值结果，其可靠性均不同程度降低。边界分析（Boundary Analysis）提供了这一类问题的解决方案。边界分析基于特定地质边界或品位边界的品位变化情况统计分析，判断地质域或品位域在进行资源量估算时是否需要合并，避免人为割裂在地质和统计意义上具有连续性的样品数据。本文以刚果（金）某铜钴矿床氧化矿资源量的估算为例，考察工业矿/低品位矿和氧化矿/硫化矿2类矿石边界的边界类型划分对品位估值的影响，以期为刚果（金）地区相似矿床的资源量估算提供新思路。

1 边界分析原理

边界分析是近20年来国内外流行的一种确定资源量估算域的有效方法^［2-13］。边界分析主要考察特定地质域或品位域边界附近矿化元素的品位变化（见图1），如果边界内外品位存在突變则该边界为硬边界（Hard Boundary），反之如果品位是渐变变化则为软边界（Soft Boundary）或半软边界（Semi-soft Boundary）。硬边界条件下，仅采用域内数据进行估值；软边界条件下，采用域外一定范围内样品数据进行估值。边界分析一般步骤为：①确定研究边界，该边界可以是地质边界（如构造面、氧化还原界面、岩性界面、蚀变带界线），也可以是品位边界（如矿岩边界、工业矿体与低品位矿体边界）；②开展边界附近品位统计，计算样品点到边界距离和特定距离内的样品点平均品位；③采用样品点平均品位与离边界的距离作图进行判别。ABZALOV等^［8-9］对边界分析的原理和方法进行了系统介绍，本文不再赘述。

边界分析的目的在于判断地质域（Geological Domain）或品位域（Grade Domain or Grade Shell）在进行资源量估算时是否需要合并，以最终确定采用哪些样品数据参与品位估值。估算域（Estimated Domain）划分过小会导致参与资源量估算的样品数据太少，而影响品位统计分析和估值的可靠性^［7］。此外，更为重要的是，边界类型划分对品位估值结果有直接影响。如高品位域中带入大量低品位域的数据，则导致估值整体偏低；相反，原本属于软边界类型的，如果采用硬边界条件进行估值，将人为增强高品位数据的连续性^{［2-3，14］}。为了进一步说明边界类型划分的重要意义，本文用实例来说明采取硬边界和软边界的不同条件下，资源量估算结果的差异。

2 刚果（金）某铜钴矿床地质及数据特征

研究案例位于刚果（金）铜钴成矿带西段。区域内铜钴矿床产出受层位控制，矿床形成经历了多期多阶段演化。该铜钴矿床矿体呈东西走向，倾向南，倾角60°～80°，平均65°（见图2）。主矿体长约1 000 m，厚30～50 m，埋深1 150～1 368 m。为满足湿法冶金工艺要求，按照80 %氧化率（酸溶铜/全铜）将主矿体分为上部氧化矿和下部硫化矿（见图2-b）。氧化矿和硫化矿界面标高在1 280 m。矿床采用钻孔和槽探联合控制，基本勘查工程间距为100 m×50 m，生产勘探阶段加密到25 m×25 m。基本采样间距2 m。基本分析样品为4 768件，铜品位为0.01 %～26.06 %，平均值为1.44 %，方差为4.26×10^-4，变异系数（Cv）为1.43。为便于统计分析，对原始样品数据进行2 m等长组合。组合后样品为4 204 件，铜品位为0.01 %～21.73 %，均值为1.54 %，方差为3.61×10^-4，变异系数为1.23。

采用分形方法^［15］确定铜矿化域为0.45 %～16.00 %（见图3）。对等长样品数据进行特高值处理，铜品位大于16.00 %的用16.00 %代替。共对18.44 %、19.04 %、19.73 %、20.64 %和21.73 %等5个特高品位数据进行了处理。样品数据中的缺省数据用0代替。

用矿化域边界品位0.45 %和推荐的工业边界品位1.00 %进行矿（化）体圈连（见图2-b）。用0.45 %边界品位圈矿时，不剔除夹石，根据矿化体产状特征，尽可能将更多的工程见矿或见矿化地段圈入。用1.00 %工业边界品位圈矿时，剔除夹石，尽可能减少非工业品位样品的带入。

3 基于地质域和品位域的边界分析

按照勘查规范要求，不同的地质域应单独圈定并分开估值^［9］。因此，要对氧化铜矿石资源量进行估算，首先要按照铜工业边界品位圈定氧化矿地质域，并且用域内数据进行估值。氧化礦中带入大量低于工业品位数据或利用混合矿、硫化矿地质域内数据参与氧化矿品位估值，都是不允许的。然而，基于边界分析的原理，域外数据是否参与资源量估算主要取决于域边界的类型。

结合研究目的，以氧化矿石为主要对象，分别考察品位域和地质域的边界条件（见图4）：①工业氧化矿体（铜品位为1.00 %）构成的工业品位域边界类型，以判断矿化品位域（铜品位为0.45 %～1.00 %）内数据是否参与估值；②工业氧化矿体构成的氧化矿地质域边界类型，以判断硫化矿地质域内数据是否参与估值。

由图4可知：边界附近的品位为渐变变化特征，工业矿品位域/低品位矿品位域及氧化矿地质域/硫化矿地质域的边界类型均为软边界。换言之，可以考虑将工业矿品位域与低品位矿品位域合并，或者氧化矿地质域与硫化矿地质域合并，用合并后的估算域进行品位估值和资源量估算。结合本文的应用，考虑分别用矿化样品品位数据和氧化矿+硫化矿样品数据对氧化矿体进行估值。

4 氧化矿石资源量估算方案

4.1 估算域的设计

为了便于比较不同边界条件对资源量估算的影响，设计了4种估算域模型（见图5、表1）。Case1为传统方法，剔除特高品位后，用工业边界品位圈定氧化矿体，根据地质认识圈定矿体中夹石，估值时全部采用工业氧化矿体内数据。Case2是Case1将工业品位域扩展到矿化品位域，同时保留了夹石，不扣除。Case3是Case1将工业氧化矿地质域扩展到工业氧化矿+硫化矿地质域，同样扣除了夹石。Case4是Case1同时进行品位域和地质域的扩展，不扣除夹石的结果。按上述4种情形圈连矿体，并创建块模型。块模型中块体积为10 m×4 m×4 m，次分块体积为5 m×2 m×2 m。按氧化矿石密度2.42 t/m3、硫化矿石密度2.62 t/m3，分别统计出4种模型的体积和吨位。

4.2 统计分析及IDW估值参数确定

对设计的4种估算方案，分别统计估算域内数据特征，并进行变异函数的块金效应和最优滞后距拟合。统计和拟合结果见图6。Case1等长组合样品数1 726，品位0～16.0 %，平均值2.926 %，方差3.724×10^-4，变异系数0.659；块金值0.455×10^-4，块金效应12.2 %，最优滞后距40 m。Case2等长组合样品数2 401，品位0～16.0 %，平均值2.267 %，方差3.871×10^-4，变异系数0.868；块金值0.20×10^-4，块金效应5.2 %，最优滞后距50 m。Case3等长组合样品数1 929，品位0～16.0 %，均值2.844 %，方差3.493×10^-4，变异系数0.657；块金值0.416×10^-4，块金效应11.9 %，最优滞后距50 m。Case4等长组合样品数2 960，品位0～16.0 %，平均值2.042 %，方差3.582×10^-4，变异系数0.927；块金值0.176×10^-4，块金效应4.9 %，最优滞后距50 m。

变异函数拟合结果显示，块金效应在4.9 %～12.2 %，为低块金效应，适合采用4～5的高幂次^［13］，本文选用5；最优滞后距为40～50 m，本文选用50 m，与基本勘查工程间距一致。根据矿体产状，确定搜索椭球参数为：走向90°，倾角-65°，倾伏角0°；设置扇区个数为8，最多样品数6，最少为3；探明资源量搜索半径为60 m，控制资源量搜索半径为120 m，推断资源量搜索半径为180 m。基于上述参数，分别对4种块模型开展IDW估值。

5 估算结果及讨论

5.1 块模型结果

4种块模型的估算结果见图7、图8。由图7、图8可以看出，采用硬边界条件时（见图7-a）、c），图8-a）、c）），块模型内几乎全部为工业品位块（铜品位≥1.0 %）；采用软边界条件时（见图7-b）、d），图8-b）、d）），由于未扣除夹石，块模型内既有工业品位块，也有低品位块和无矿块。此外，不同边界条件下高品位块（红色块）的连续性存在明显差异，硬边界条件时高品位块的连续性显著增强。

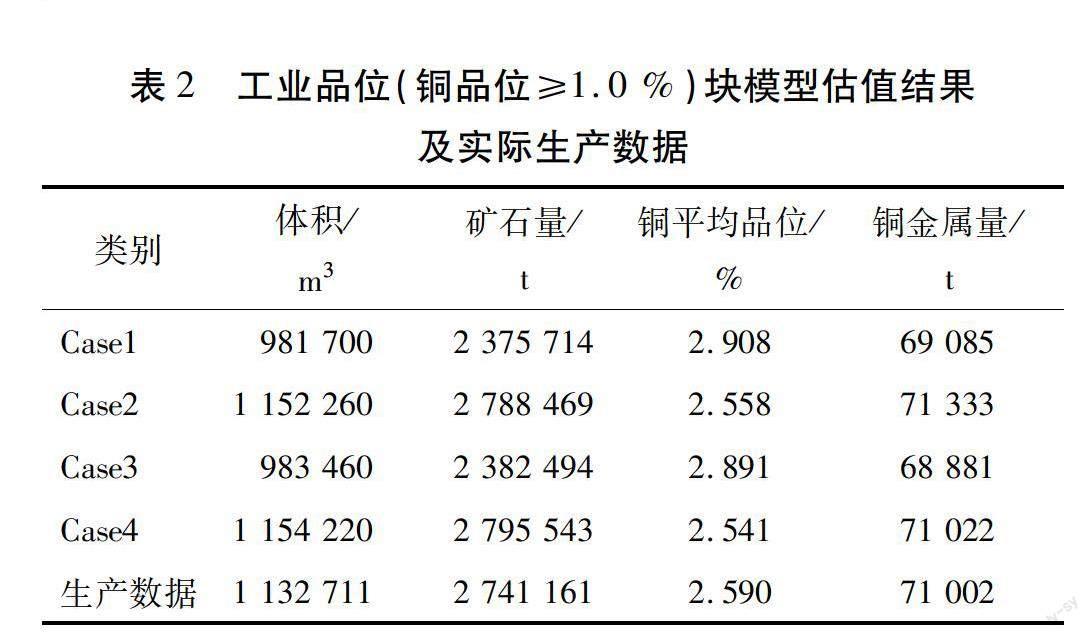
5.2 资源量估算结果与实际生产数据的比较

工业品位（铜品位≥1.0 %）块模型估值结果及实际生产数据见表2。由表2可知：硬边界条件下的工业品位块模型体积、矿石量、金属量低于实际生产数据，而铜平均品位显著高于生产数据。软边界条件下，工业品位块模型的体积、矿石量略高于生产数据，而铜平均品位稍低于生产数据，铜金属量与实际生产数据基本一致。

4种块模型不同台阶铜平均品位估值结果见图9。由图9可知：软边界条件下，上部台阶铜平均品位整体高于生产数据，下部台阶铜平均品位整体低于生产数据。硬边界条件下，铜平均品位整体显著高于生产数据。

5.3 边界条件对品位估值的影响

硬边界圈矿容易遗漏工业矿体^［16］。本文案例中，硬边界圈矿的工业矿块体积约为98万m3，明显小于软边界圈矿的工业矿块体积（约115万m3）。这表明，有大量实际存在的矿石并未圈入工业矿体，导致硬边界条件估算的总金属量比实际生产数据少了2 000 t左右。采用硬边界条件进行估值的另一个风险就是矿块品位的系统性高估。IDW方法和克里格等估值方法一样，存在平滑作用和条件偏差，即高值低估和低值高估（见图9）。而在硬边界条件下，高品位的连续性增强，不论是分台阶的估值结果还是总体估值结果，都存在显著的品位高估（见图8、图9、表2）。估算品位偏高而生产数据较低，既影响企业经济效益，又打乱了矿山正常规划及产量、处理量、选冶指标稳定性等日常生产。

传统圈矿扣除夹石，进一步增强了硬边界条件。与此同时，夹石的圈定过多凭地质工程师的经验和对项目的认知，人为因素较多。由图7和图8可知：采用软边界条件时，即使在圈矿时没有扣除夹石，最终的估值结果也较好地显示了夹石形态。而且，最终的夹石形态也是IDW估值的结果，因而块模型的协调性更好。

应用软边界条件的优点是多方面的：①考虑了样品数据在地质上和统计上的连续性。自然界中，除沉积矿床、角砾岩型矿床和块状硫化物矿床等的矿体与围岩界线是突变外，大部分矿化受构造和蚀变作用控制的矿床，从礦体到围岩的品位变化往往呈渐变过渡特征。例如：斑岩型矿化、大部分热液矿床、表生富集矿床等，适用于软边界条件进行建模和估值。②基本不会遗漏工业矿体。软边界条件不仅增加了块模型的总体积，也相应增加了工业品位矿块的体积。通过考察4种块模型中工业品位矿块体积与块模型总体积的比例不难发现，硬边界条件下Case1和Case3块模型体积约为99万m3，其中工业品位矿块体积约为98万m3，占比达99 %；软边界条件下Case2和Case4块模型体积为133万～135万m3，其中工业品位矿块体积约115万m3，占85 %～86 %（见表1、表2）。扩展的矿化域几乎包含了所有可能出现的工业矿体。此外，当市场条件发生变化，尤其是价格上涨时，不用重新建模圈定工业矿体，而可以通过降低块模型的边界品位，输出工业品位矿块资源量估算结果，实现“一次建模估值，长期受益”。③建模和估值流程简单快捷，技术重复性强，易于操作和推广。当前矿山智能化发展的重要趋势是减少人为干预，把标准化估值流程问题交给数学算法，较好迎合了这一要求。

6 结 论

本文简要介绍了边界分析的原理和方法，并以刚果（金）某铜钴矿床氧化矿资源量估算的实际案例进行了应用。研究工作得出以下主要结论：

1）边界分析为氧化矿是否应单独圈矿估值，判断是否采用矿化域进行资源量估算，提供了统计学上的方法和依据。

2）采用工业品位圈矿和进行夹石扣除的硬边界条件，往往增强高品位数据的连续性，导致估值品位显著增高。

3）采用软边界条件进行建模和估值，考虑了样品数据在地质和统计上的连续性，估值准确度高，不会遗漏工业矿体。该方法流程简单快捷，技术重复性强，易于操作和推广。

［参 考 文 献］

［1］ 国家市场监督管理总局，国家标准化管理委员会.固体矿产地质勘查规范总则：GB/T 13908—2020［S］.北京：中国标准出版社，2020.

［2］ STEGMAN C L.How domain envelopes impact on the resource estimate-case studies from the Colar gold field NSW，Australia［M］∥ EDWARDS A C.Mineral resource and ore reserve estimation—The AusIMM Guide to Practice.Victoria：The Australasian Institute of Mining and Metallurgy，2001：221-236.

［3］ SINCLAIR A J，BLACKWELL G H.Applied mineral inventory estimation［M］.Cambridge：Cambridge University Press，2002：1-401.

［4］ ORTIZ J M，EMERY X.Geostatistical estimation of mineral resources with soft geological boundaries：A comparative study［J］.The Journal of the Southern African Institute of Mining and Metallurgy，2006，106（8）：577-584.

［5］ EMERY X，ROBLES L N.Simulation of mineral grades with hard and soft conditioning data：Application to a porphyry copper deposit［J］.Computational Geosciences，2009，13（1）：79-89.

［6］ WILDE B J，DEUTSCH C V.Kriging and simulation in presence of stationary domains：Developments in boundary modeling［M］∥ABRAHAMSEN P，HAUGE R，KOLBJRNSEN O，et al.Geostatistics Oslo 2012，quantitative geology and geostatistics 17.Berlin：Springer，2012：289-300.

［7］ ROSSI M E，DEUTSCH C V.Mineral resource estimation［M］.Berlin：Springer，2014.

［8］ ABZALOV M Z.Applied mining geology［M］.Berlin：Springer，2016.

［9］ 高帮飞.资源量估算的边界分析与矿化体圈定［J］.地质与勘探，2018，54（2）：415-425.

［10］ 高帮飞，李红兵，张书琛，等.块金效应地质意义及其对品位估值影响［J］.黄金，2021，42（11）：6-13.

［11］ 李红兵，高帮飞.岩金矿床资源储量估算品位域的确定及其意义［J］.黄金，2021，42（4）：6-11.

［12］ 謝徽，高帮飞，李寒滨，等.内蒙古常福龙金矿床隐式地质建模与品位估值［J］.黄金，2022，43（4）：4-13.

［13］ 陈伟康，高帮飞，张书琛，等.距离幂次反比法（IDW）资源储量估算流程改进及应用［J］.中国矿业，2022，31（4）：181-188.

［14］ GLACKEN I M，SNOWDEN D V.Mineral resource estimation［M］∥EDWARDS A C.Mineral resource and ore reserve estimation—The AusIMM Guide to Practice.Victoria：The Australasian Institute of Mining and Metallurgy，2001：189-198.

［15］ 高帮飞，谢徽，沈阳，等．一种确定资源储量估算的品位域的方法：201611040814.3［P］．2017-05-31．

［16］ SRIVASTAVA R M.Probabilistic modeling of ore lens geometry：An alternative to deterministic wireframes［J］.Mathematical Geology，2005，37（5）：513-544.

Oxide ore resource estimation of a Cu-Co Deposit

in the Democratic Republic of Congo based on boundary analysis

Xie Hui

（Beijing Technical Consulting Branch of China Railway Resources Group Co.，Ltd.）

Abstract：In the traditional method of oxide ore resource estimation，the industrial grade is usually used for the delineation of ore bodies，and the data in the ore bodies are used for the estimation.Case studies show that traditional methods can enhance the continuity of high-grade data in the industrial grade domain which leads to a significant overestimate of ore grades.Boundary analysis can judge the boundary type by examining the sample grade changes within a certain range of the boundary of a specific geological domain or grade domain.Under the hard boundary condition，only the data in the industrial grade domain are used for estimation，while under the soft boundary condition，the data in the mineralization domain should also be involved in the resource estimation.The actual case study shows that the use of soft boundary conditions for modeling and estimation and the considerations of the geological and statistical continuity of sample data lead to high estimation accuracy without missing industrial ore bodies.The method has the advantages of a simple and rapid process，and strong technical repeatability，and should be promoted as an improved resource estimation method.

Keywords：inverse distance power;fractal analysis;variogram;hard boundary;soft boundary;horse rock;resource estimation