星地融合网络的上行链路覆盖性能分析模型*

李春若，苑俊英

（1.江西财经职业学院南昌校区信息中心，南昌 331700；2.广州南方学院电气与计算机工程学院，广州 510970）

0 引言

星地融合网络将在现有地面5G 网络的基础上支持更加丰富的业务［1-2］，为大型无线物联网网络的部署提供通信支持。智慧农业、资产跟踪、环境感知等应用需要在偏远地区部署海量的物联网传感节点。然而，由于技术困难和成本限制，地面网络难于无缝地覆盖偏远地区和海上区域。

因此，将地面技术与卫星技术进行融合十分必要。通过地面网络与卫星网络的融合［3-4］，提高对地面和海上区域的覆盖质量。通过卫星对地面基础设施的补偿性覆盖，确保覆盖的连续性。

与地面基站不同，卫星通常非常昂贵，且部署时间长。然而，为了实现地面用户设备的无缝覆盖，需要部署大量的卫星。这就要求拟定部署计划，即讨论覆盖质量与部署成本间的权衡之策，理论分析为部署计划提供有效的数据支持。

通过理论分析，可有效地洞察不同参数对星地网络的性能。来自随机几何的工具被广泛用于捕获星地网络的性能。借助这些工具，可有效分析卫星网络性能［5-6］。尽管现有文献对星地融合网络进行了不少研究，但仍缺乏确保上行链路覆盖的分析模型。

为此，针对星地融合网络的上行链路覆盖问题，提出基于覆盖概率的星座数和基站数的分析模型（AMCP）。主要工作如下：1）针对星地融合网络的上行链路覆盖概率问题，提出一个分析模型；2）推导了在满足一定覆盖概率的条件下，卫星数与基站数间关系，即卫星数和基站数对覆盖概率的影响；3）分析了卫星星座设计对覆盖的影响，分析表明，可通过增加卫星数或者基站数提升覆盖用户数量。

1 系统模型

1.1 随机几何

将卫星星座、基站和用户的位置定义为独立的质点。将卫星随机部署于高度为h 的星座球面上，每个卫星在随机圆轨道内移动，且所有卫星所在的圆轨道半径相同。

值得注意的是，随机几何模型将卫星看成点［7-8］，并且这些点在球面上的位置是随机的。而现实应用是以确定方式部署卫星。然而，确定性部署星座要求复杂的数学模型。

为了降低模型的复杂度和便于处理，本文将卫星星座的部署看成同构的泊松点过程（poisson point process，PPP）［5］。假定星座由Ns个卫星组成，这些卫星在高度为h 的球面上运行。因此，卫星密度的平均值为：

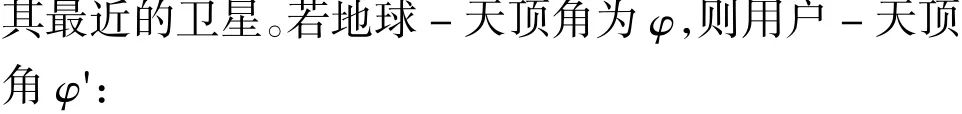
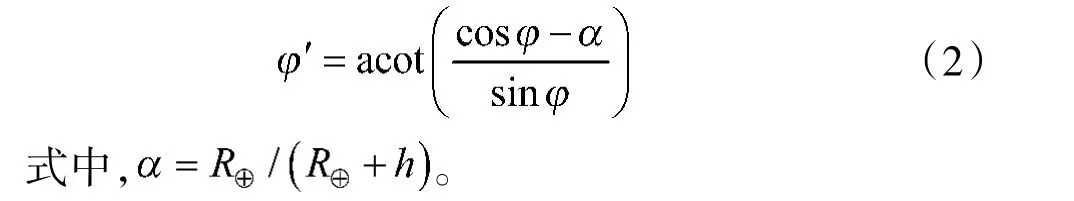
图1 地球-天顶角示意图Fig.1 Schematic diagram of the earth-zenith angle

参照文献［5］，常数角φ0的概率密度函数（probability density function，PDF）：

类似地，将地面基站位置看成独立、同构的PPP 过程，并假定用户和基站均位于地球表面。同时，假定每个用户连接至离其最近的基站。由于用户和基站均在地面表面，它们间的距离相比于地面的半径很小。在这种情况下，可将地面表面看成是平面。因此，将用户与基站间距离简化为已知的二维PPP 模型，且其常数距离R0的PDF 为［9］：

2 AMCP 模型

2.1 信道模型

星地融合网络中主要涉及两类信道：地面至卫星信道和用户至地面基站信道。对于地面至卫星信道，考虑文献［10］的经验模型。在该模型下，卫星端所接收的信号功率Ss：

式中，θ 表示地面用户的仰角；β 是环境相关的参数。

对于用户至地面基站信道，考虑通用的对数路径衰耗模型。因此，地面基站端所接收的信号功率为：

式中，a 表示路径衰落指数；b 是衰耗模型的常数；g是路径损耗指数。

2.2 上行链路的干扰

在星地融合网络中，卫星和地面基站均对用户信号均形成干扰。

2.2.1 卫星对地面用户形成的干扰

图2 卫星足迹示意图Fig.2 Schematic diagram of satellite footprints

引用Is的平均值表述对系统性能的影响。依据文献［10］的Campell 理论，计算Is的平均值：

2.2.2 地面基站对用户信号形成的干扰

基站对用户信号也形成干扰。与2.2.1 节类似，基站对用户xo信号所形成的干扰为：

式中，ri表示用户xi离用户xo的距离；κb表示干扰因子；hi表示用户xi的高度。

2.3 覆盖概率

在星地融合网络中，用户既可通过地面基站，也可通过卫星星座传输信号。因此，只有同时符合以下两个条件，则认为传输失败。1）卫星链路的信干比（signal-to-interference-and-noise ratio，SINR）［12］γs小于服务的门限值γ0；2）地面基站与用户间链路的SINRγb小于门限值γ0。因此，融合网络中对用户的成功覆盖的概率（以下简称覆盖概率）为：

3 性能分析

3.1 仿真参数

通过蒙卡洛仿真分析AMCP 模型的性能。利用蒙卡洛仿真产生3 个独立的随机过程：1）在幅度为的球体上随机地部署卫星位置；2）在地球表面上随机地部署地面基站；3）在地球表面上随机部署用户。此外，假定地球是圆的，且半径为。表1 给出了仿真参数。

表1 仿真参数Table 1 Simulation parameters

3.2 覆盖概率

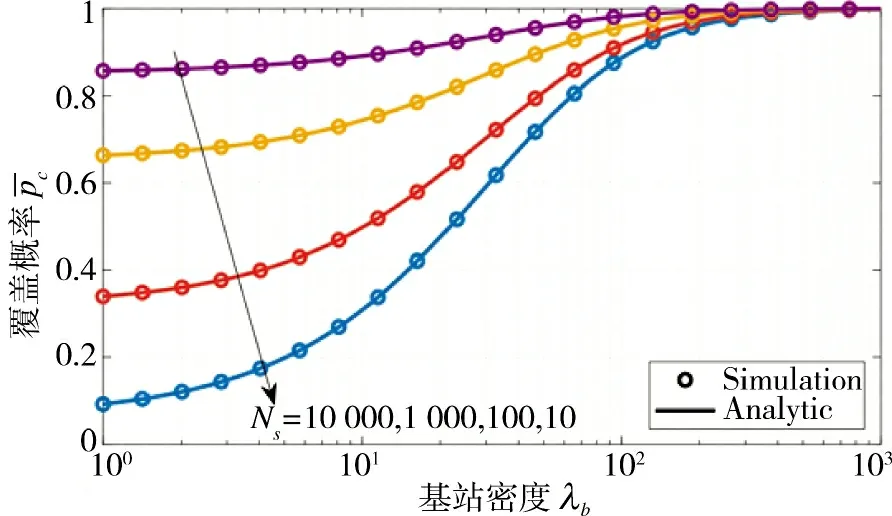
图3 覆盖概率Fig.3 Coverage probability

由图3 可知，在基站密度较低阶段，卫星链路质量决定了覆盖概率。例如，基站密度为1 时，Ns=10 000 的覆盖概率约0.85；而Ns=10 的覆盖概率跌至0.1。覆盖概率随基站密度的增加而上升，当基站密度达到100 时，Ns=10 000、Ns=1 000、Ns=100、Ns=10 四种情况下的覆盖概率趋于收敛。此外，理论分析与仿真相符，说明本文推导工作的正确性。

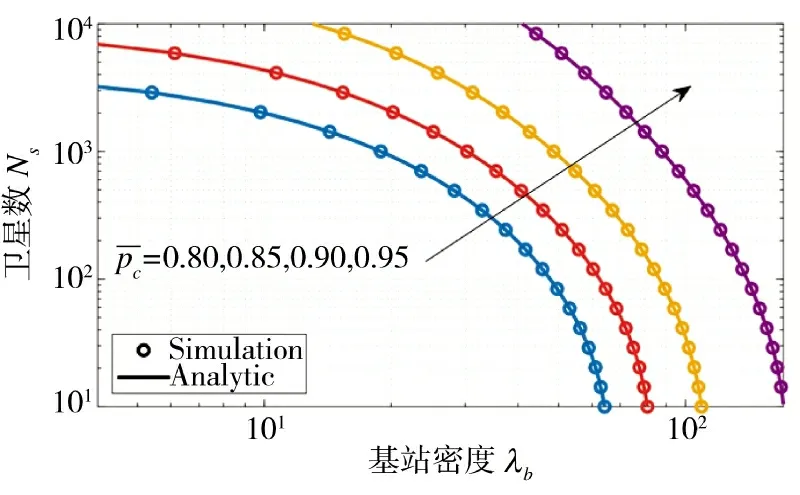
图4 卫星数和基站密度对覆盖概率的影响Fig.4 Impact of numbers of satellite and density of base stations on coverage probability

3.3 卫星数和基站密度对覆盖概率的影响

3.4 卫星星座的设计对卫星数的影响

本节重点分析卫星星座设计对卫星数Ns的影响。即在维护覆盖概率=0.8 时，分析PPP，Walker-delta 和Walker-star 3 类设计对所需的卫星数的影响。值得说明的是：提出的AMCP 模型采用了PPP；而Walker-delta 和Walker-star 属倾斜圆轨道星座设计，它们的倾斜角分别为86.4°和53°，高度均500 km。图5 中将Walker-delta 和Walker-star分别标识为Walker-Δ 和Walker-*。

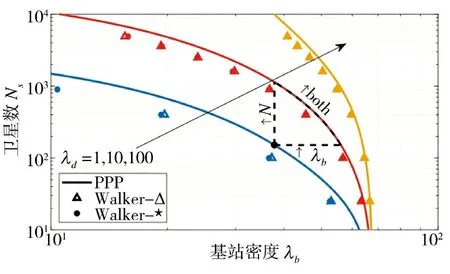
图5 卫星星座设计对卫星数Ns 的影响Fig.5 Impact of satellite constellation design on the number of satellites

由 图5 可 知，相 比 于 Walker-delta 和Walker-star，PPP 星座设计策略需要更多的卫星数才能达到覆盖概率=0.8。原因在于：Walker-delta 和Walker-star 的星座部署更符合实际情况，但它的数学模型比PPP 复杂。

4 结论

本文提出一个分析模型，该模型分析卫星星座数和基站密度对星地融合网络的覆盖概率的影响。该模型利用来自随机几何的工具产生星地融合网络的3 个随机过程，构建基于覆盖概率的星座数和基站数的分析框架。该模型为设计星地融合网络提供了参考。