基于LSTM神经网络的压电执行器位移迟滞建模

时梦想,胡 泓,吴 浩,徐希潇

(1. 哈尔滨工业大学(深圳)机电工程与自动化学院,广东 深圳 518000;2. 深圳市西渥智控科技有限公司,广东 深圳 518000)

0 引言

LED芯片生产过程中,在经过前道加工步骤后,晶圆片(Wafer)上芯片的数目从几千到数万不等。为了控制质量和降低后续工序生产成本,需要对每颗芯片通电后进行光电参数测试。在半导体测试领域,生产线上大多采用探针结构通电。目前工业上探针与芯片电极的接触和脱离一般通过传统步进或伺服电机带动。压电执行器作为一种新型的执行机构,具有工作精度高,响应速度快及驱动力大的优点,使其适用于各种应用场景[1]。本文研究的压电执行器主要应用于LED芯片测试过程中。使用末端带有探针的压电陶瓷执行器实现探针和芯片电极接触并进行测量。提高芯片测试效率和探针位移精度。但压电执行器位移与驱动电压存在非线性关系,主要源于压电陶瓷的迟滞效应。迟滞效应导致压电执行器的输出位移不仅与当前驱动电压有关,还与之前的驱动电压有关。一般迟滞效应会随着驱动电压的频率改变而改变,这给精确控制压电执行器的位移带来了挑战。为了解决这个问题。一方面使用闭环控制方法,可以达到较理想的位移控制效果,但闭环控制需要为压电执行器额外配置位移传感器,增加了使用成本和系统复杂度。另一方面使用基于位移迟滞模型的开环控制方法,但此方法的迟滞模型对于位移预测需要有足够精度。因此,研究者提出各种模型用于迟滞效应的建模。其中数学解析模型一般具有大量的参数,识别过程较难。静态的迟滞模型包括Preisach模型、Prandtl-lshliskii(PI)模型及Maxwell模型等[2]。

深度学习可模拟非线性映射关系[3],已有很多研究者使用神经网络对压电迟滞效应进行建模[4]。郭岱宗等[5]使用循环神经网络(GRU)对压电执行器位移迟滞进行建模,与传统的数学模型相比,该模型具有较好的模拟迟滞效果。邹守睿等[4]设计了一种循环神经网络对压电驱动器的迟滞特性进行建模,进而得到能够准确模拟输出位移和输入电压之间关系的逆模型,并据此对压电驱动器进行前馈补偿。本文研究了使用长短期记忆(LSTM)神经网络模拟迟滞的可行性。

本研究基于一种杠杆式压电执行器[6],使用3层LSTM神经网络对执行器位移迟滞进行建模,并将所提出的基于LSTM神经网络迟滞补偿模型与传统Prandtl-Ishlinskii补偿模型进行对比,证明了神经网络模型具有更好的模拟压电执行器压电位移迟滞的效果。

1 实验方法

1.1 LSTM神经网络

压电迟滞现象主要由于压电执行器当前时刻的位移输出不仅受当前时刻电压输入的影响,还与过去时刻的电压输入有关。LSTM是一种特殊的循环神经网络(RNN),LSTM的提出主要是为了解决序列预测的问题,在预测当前时间点输出时考虑以往时间点的输入,这种预测方法与迟滞现象发生的本质吻合。

LSTM由一系列的LSTM细胞(Cell)组成,每个细胞含有若干个LSTM单元(Unit)。每个时间步的细胞状态ct存储了经过本时间步及之前的时间步筛选处理后所留存的信息,从而长记忆得以建立。

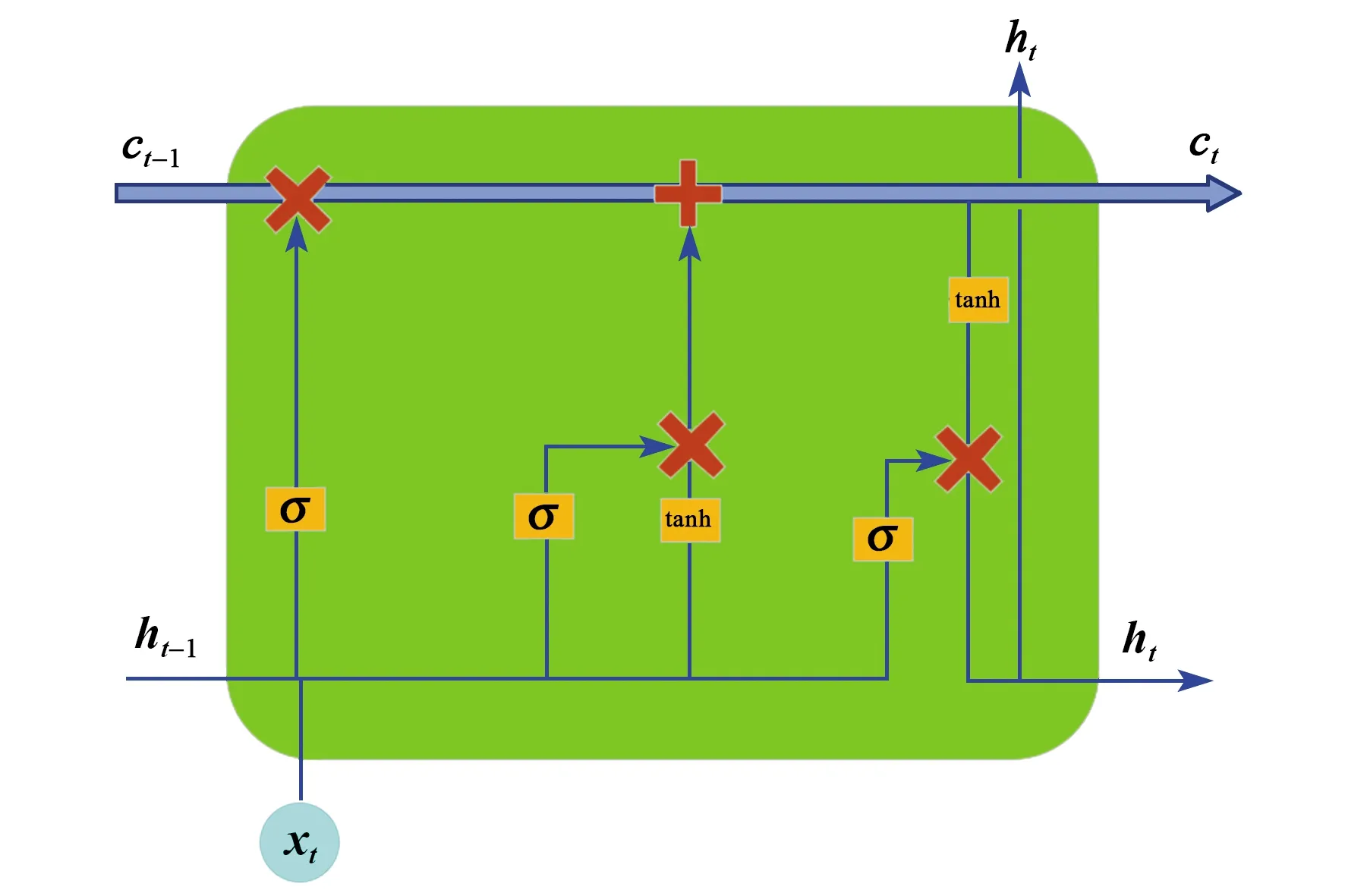
图1 LSTM神经元

ft=σ(Wfxt+Ufht-1+bf)

(1)

it=σ(Wixt+Uiht-1+bi)

(2)

ot=σ(Woxt+Uoht-1+bo)

(3)

(4)

(5)

ht=ot⊙tanh(ct)

(6)

式中:σ(·)为sigmoid激活函数,值域[0,1];tanh(·)为双曲正切激活函数,值域[-1,1];⊙为矩阵的哈达玛积(Hadamard product,按元素相乘);W,U为权重矩阵;b为偏置向量sigmoid函数和双曲正切函数的定义如下:

(7)

(8)

假设每次训练的样本数(batch size)为b,每个样本的维度为d,每个LSTM Cell隐藏神经元数(hidden size)为h。xt∈d,W,U∈h×d,ht∈h,b∈h。

1.2 神经网络超参数的选择

本文所设计神经网络由3层LSTM层和1层全连接层组成,如图2所示。

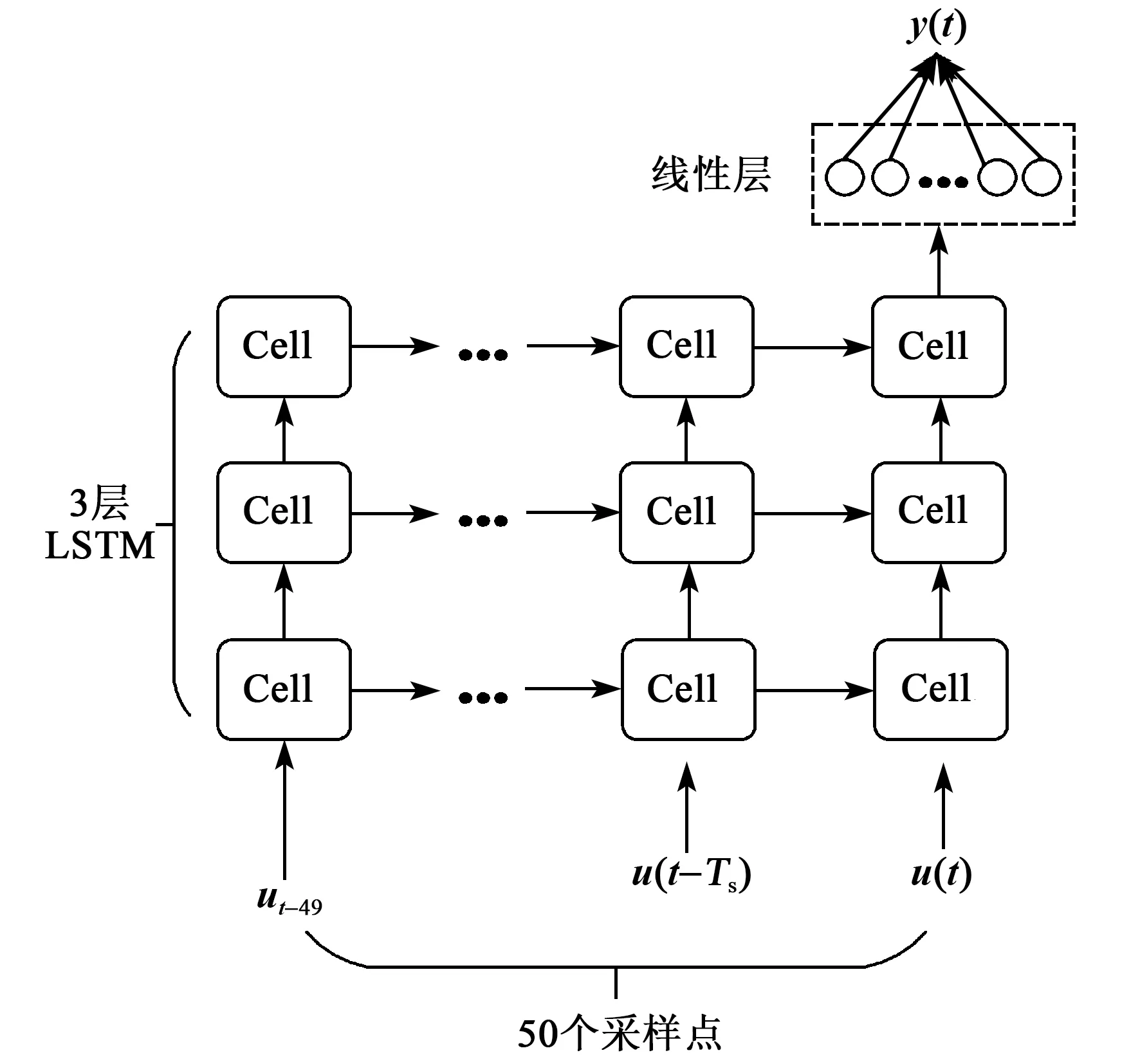
图2 神经网络结构

由于压电执行器非线性迟滞由多方面因素决定,故选取3层LSTM网络。对于多层神经网络,上一层每个Cell的输入为下面一层对应Cell的隐藏状态ht,根据实验和训练经验选取层数,更多的层数不仅可能导致较差的拟合效果,还会增加计算时间。

根据其他研究者对压电迟滞的研究,LSTM窗口大小选取为50个,隐藏单元数为64个[8],可以获得较好的拟合效果及较小的计算要求。窗口大小表示由ti时刻及其之前49个采样时刻所组成的激励电压序列ut-49,ut-48,…,ut输入到神经网络中预测ti时刻的位移yi。

由于LSTM层最终输出为ht维度(h维)的意义与实际所要预测的位移输出有差别,因此,在最后增加一层全连接层进行必要的变换。神经网络超参数如表1所示。

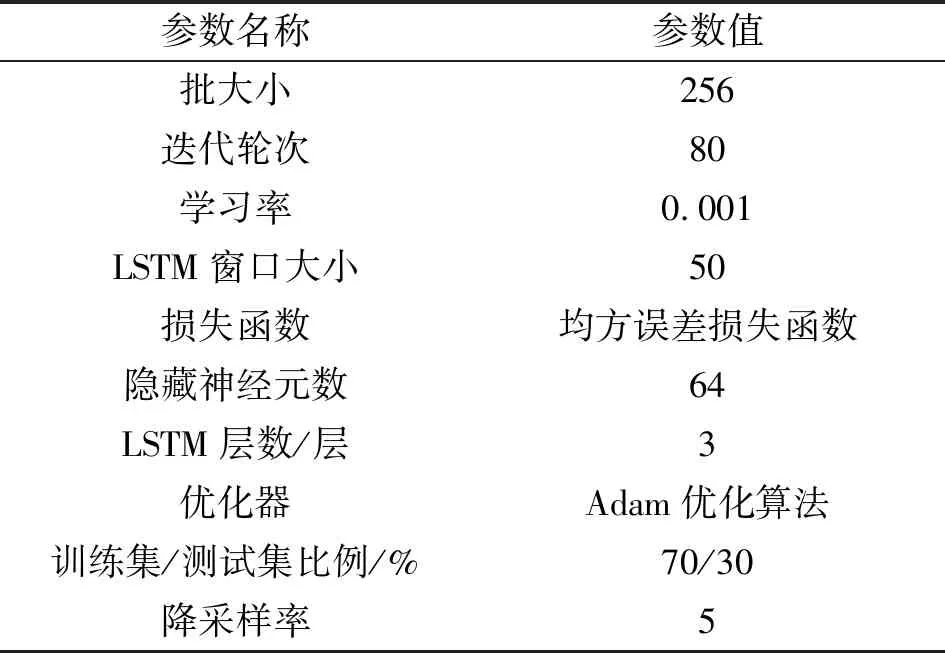
表1 神经网络超参数

1.3 经典PI模型

经典PI迟滞模型是一种数学解析模型,该模型采用双边Play算子Frj(t)和权重系数pj加权叠加来描述压电陶瓷迟滞非线性特性[2]。经典PI模型在离散处理后的表达式为

(9)

式中:rj为离散阈值(r0=0);pj为每个迟滞算子对应的权重系数,两者通过迟滞实验数据识别得出。

对每个离散的rj值,相应的迟滞算子具体计算方法为

(10)

式中z0j为各个迟滞算子初值。

为获得模型,继续对时间进行离散,每个rj值对应的迟滞算子计算方法为

(11)

式中:k=0,1,…,Ns;t0=0;tE=NsTs;Ts为采样间隔,共使用Ns+1个采用数据。

将离散后的迟滞算子和权重系数叠加,计算出压电执行器的位移输出为

(12)

2 实验系统

为了收集数据进行LSTM神经网络的训练和测试,整体的实验框图如图3所示。

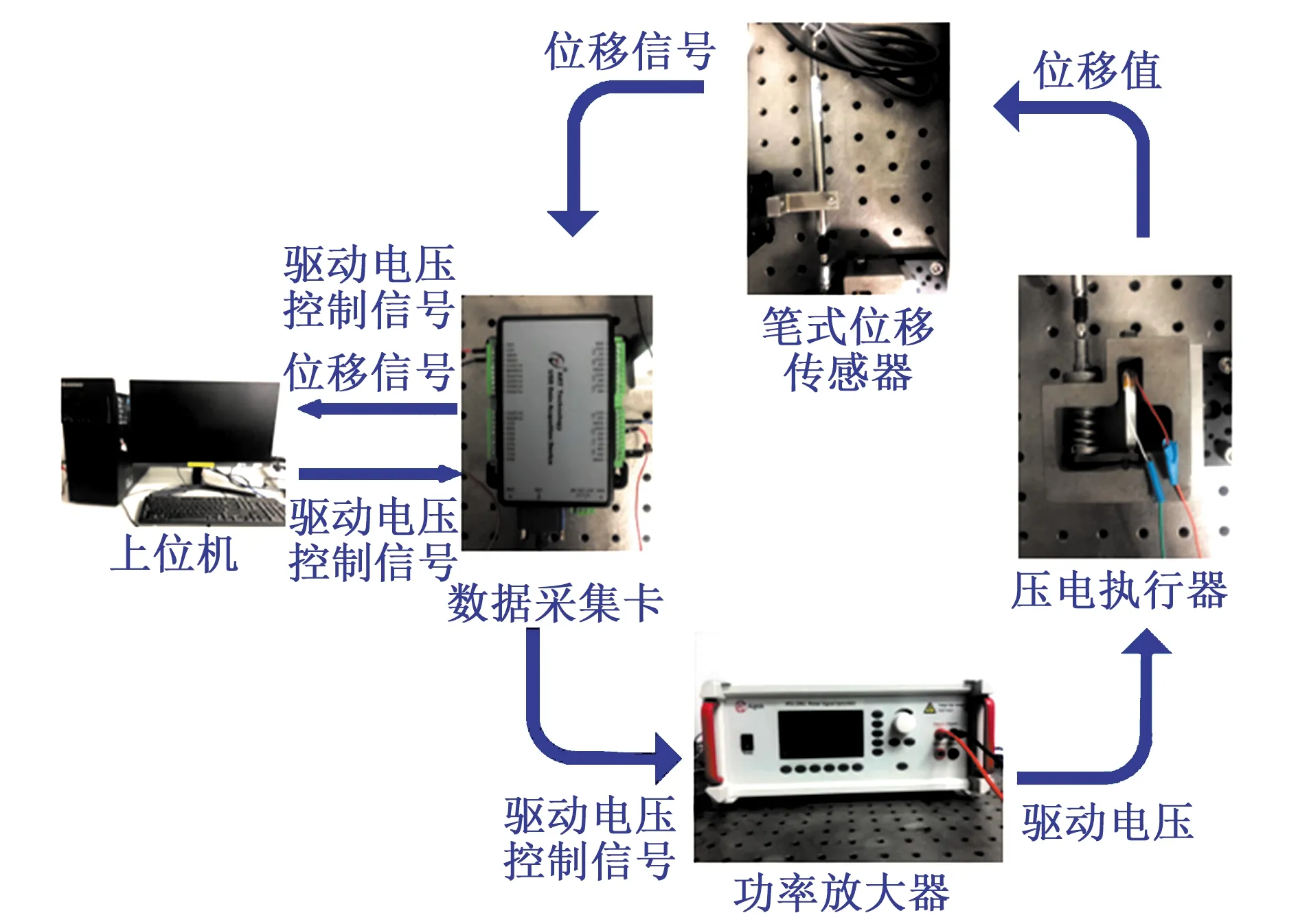
图3 实验系统

图3包含一个用于研究位移迟滞的压电执行器,其功能原理如图4所示。该执行器由杠杆机构将压电叠堆的唯一输出放大输出到末端,该压电叠堆型号为P-885.91,最大工作电压为110 V,压电执行器组装时,通过弹簧对压电叠堆施加一定的预紧力,以保证其稳定运行。

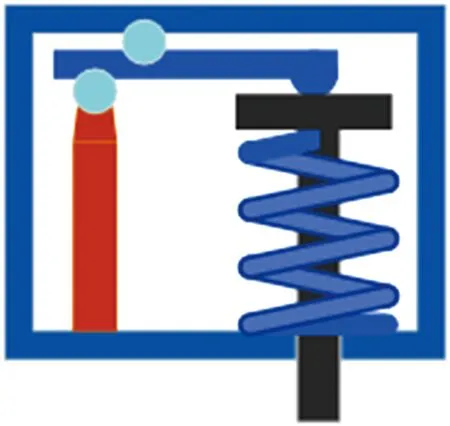
图4 压电执行器功能原理图

上位机使用Labview软件结合数据采集卡厂商的驱动程序,编写数据采集和电压控制信号发出的程序。电压控制信号通过与上位机相连的USB-5621A数据采集卡发出,输出采样频率为10 kHz。

ATG-2042型号的功率放大器将数据采集卡输出的控制信号电压进行放大,输出给压电执行器,驱动其产生位移。

位移传感器探测压电执行器的位移量,传感器选取型号为米朗LVDT8笔式传感器,该位移传感器精度为2.5 μm。最后USB-5621A将传感器位移信号的采集输入到上位机保存,位移信号和电压控制信号同步采集,采样频率均为10 kHz,最终获取压电执行器的位移迟滞信息。

3 模型辨识

3.1 模型识别训练数据获取

为了提供训练LSTM神经网络所需的多种迟滞数据,一方面使用多频率的正弦信号作为激励电压,另一方面使用多频率的衰减正弦信号作为激励电压。得到压电执行器的多个迟滞环数据,即:

(13)

(14)

式中:τ=0.15为衰减正弦波的时间常数;f为正弦波的频率;Vmax,Vmin分别为最大、最小激励电压。

由于功率放大器只能输出正电压,为防止之后的补偿电压为负值,Vmin=30 V,由于压电叠堆限制,Vmax=110 V。两种波形在1～60 Hz内各采样60组数据,传感器采样频率为10 kHz,每种信号持续20 s,共120组电压-位移数据,每种信号进行降采样后共40 000个采样点用于训练和验证神经网络模型。通过两种激励信号产生了多种迟滞环。图5为正弦波激励信号所产生的迟滞环。图6为衰减正弦波产生的迟滞环。

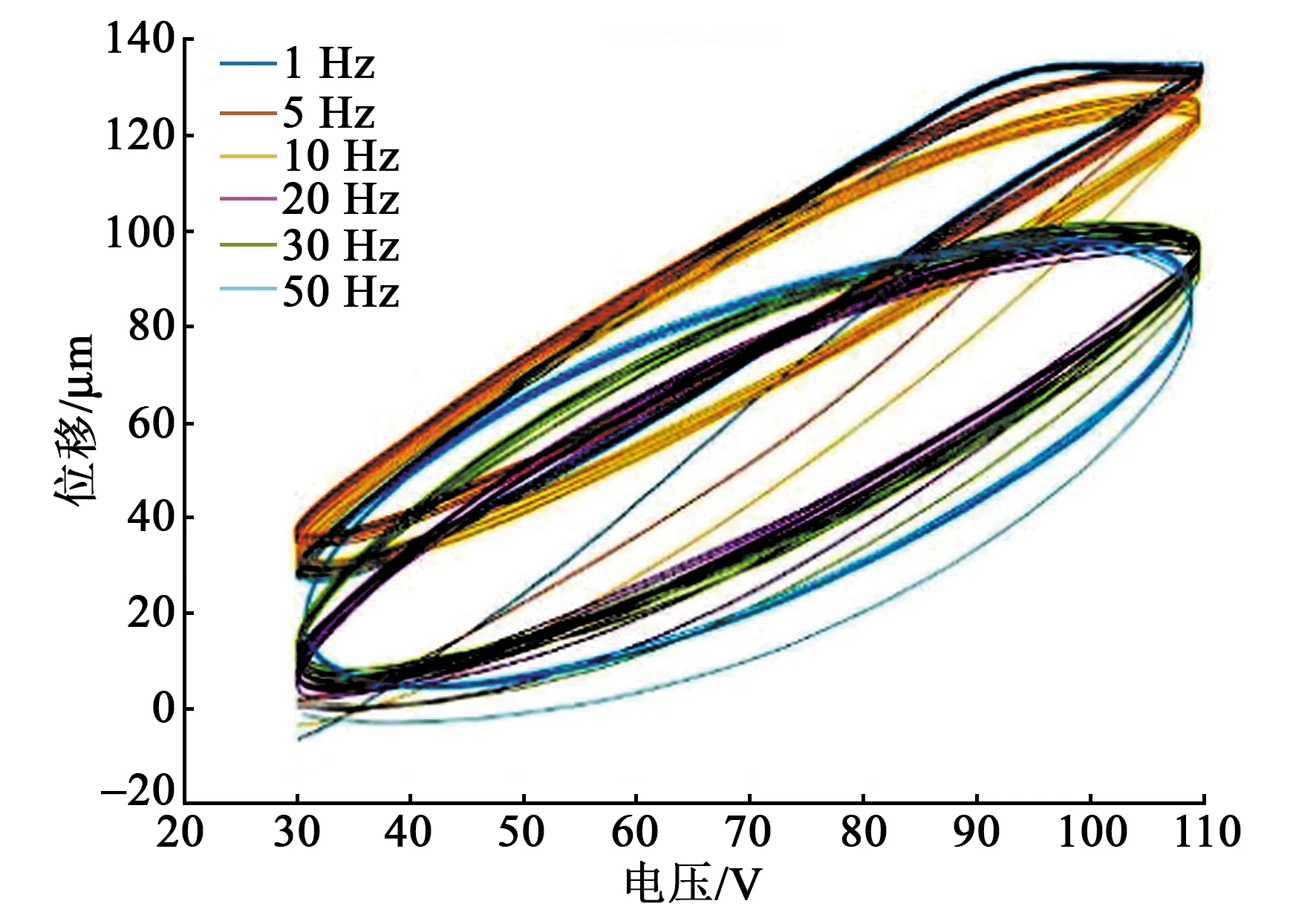
图5 正弦波激励信号产生的迟滞环

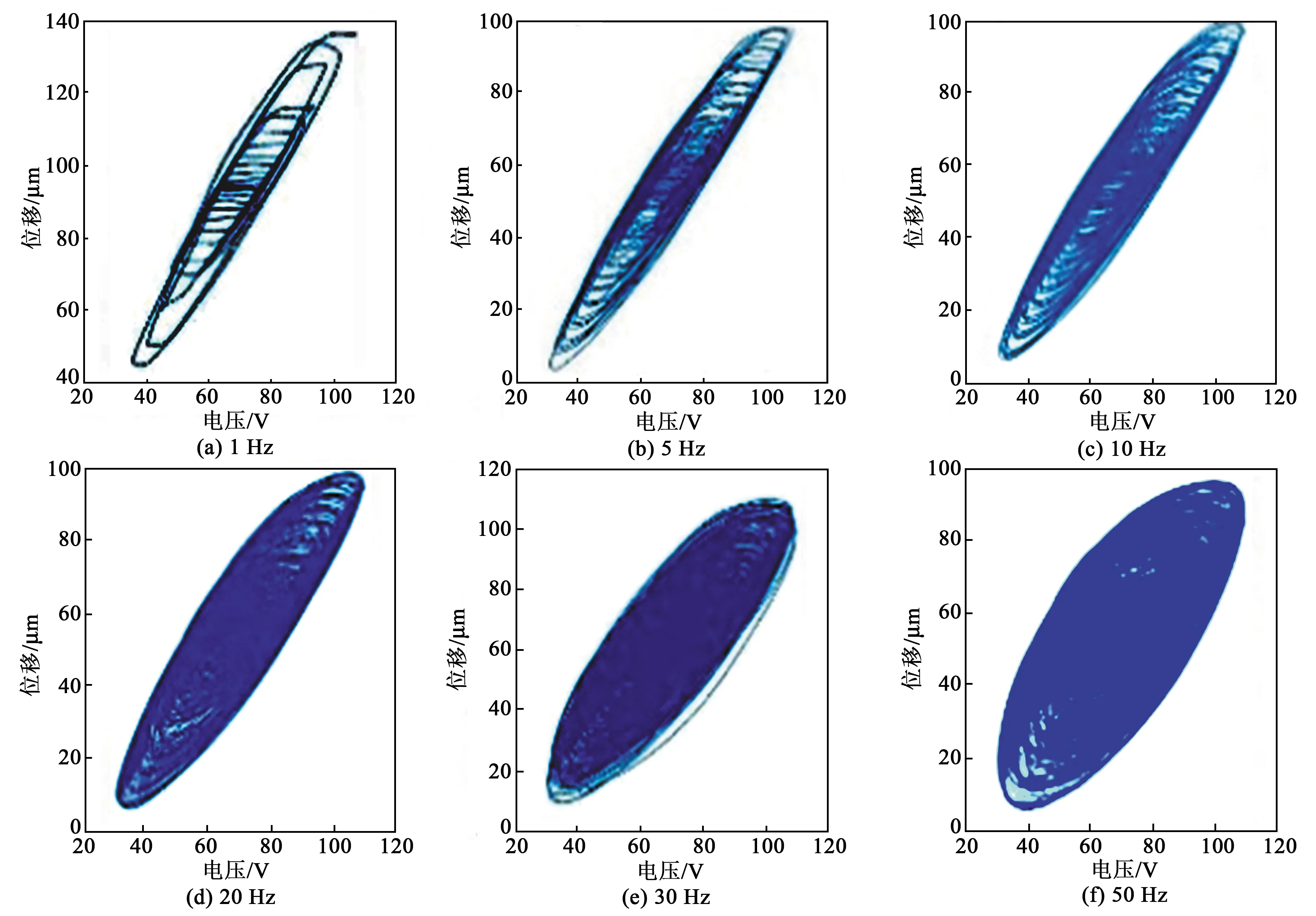
图6 衰减正弦波产生的迟滞环

由图5、6可看出,压电执行器的迟滞环与频率相关,驱动频率越高,迟滞非线性越明显,且是非对称的。这是由于压电执行器的非线性特性不仅由压电叠堆本身决定,还与机械零件之间的摩擦(如在杠杆与支点间的摩擦,顶针和顶针套间的摩擦)及零件的弹性形变有关。

3.2 LSTM训练过程

训练过程中,为提高学习效率,所有训练数据被归一化到[-1,1]区间内,与神经网络中的激活函数相匹配。使用Pytorch开源机器学习框架实现神经网络。训练迭代次数选取为80。本研究选用均方损失函数(MSE),并选择Adam算法作为反向传播优化算法,学习率设定为0.001。使用前述的神经网络及超参数训练神经网络模型。将训练集和验证集按7∶3划分。本文选取正弦波和衰减正弦波的频率为2 Hz、10 Hz、20 Hz、30 Hz、50 Hz,以此作为模型训练集和验证集数据,其他数据作为测试集数据。

训练使用计算机配置:中央处理器为Intel Xeon E5-2680 v4 CPU,主频2.4 GHz;图形处理器(GPU)为:NVIDIA Tesla P40(12TFLOPS 单精度浮点计算,47INT8 TOPS);内存为:DDR4,内存带宽达2 666 MT/s。网络需要训练的参数共有83 777个。共完成训练所需时间为30 min。训练集损失函数和验证集准确率值随迭代次数的变化曲线如图7所示。

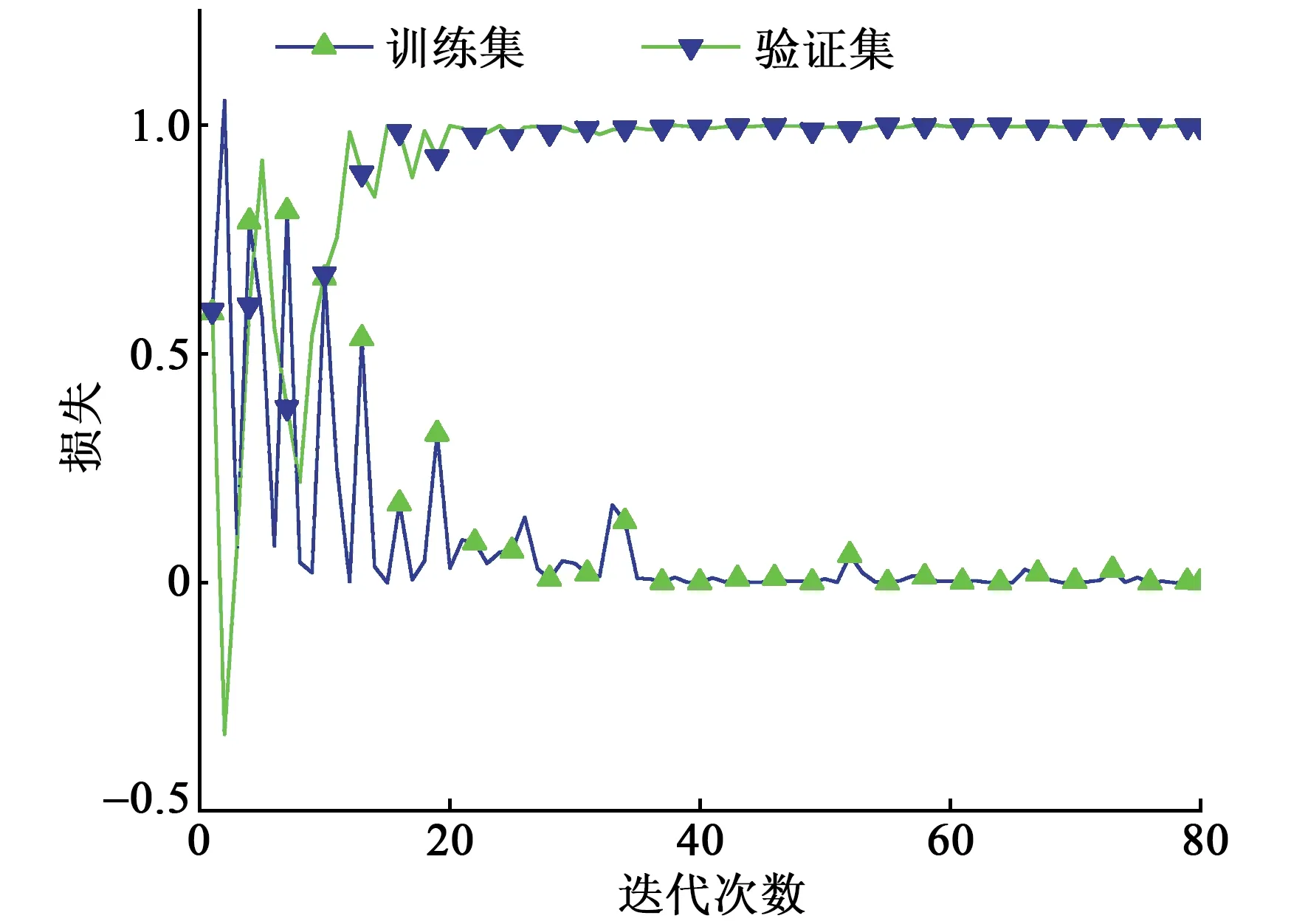
图7 损失曲线

3.3 PI模型辨识

为验证LSTM神经网络的有效性,以传统PI模型作为对照组。由于经典PI模型为静态模型,当研究分析迟滞静态特性时,输入信号频率不高,频率过高将导致模型误差过大。使用5 Hz正弦波迟滞数据进行模型参数识别。

识别PI模型首先确定迟滞算子的数量。选用迟滞算子数量越多时,模型拟合精度越高,计算量越大。本文选择迟滞算子个数为9个,阈值和迟滞算子初始值[2]为

(15)

式中电压最大值max{|v(k·Ts)|}为实际输入电压最大值110 V减去基值电压30 V,即80 V。

迟滞算子的初值均设置为0,即:

z0j=0

(16)

使用Matlab编写PI迟滞模型的识别和验证程序。权重系数计算使用最小二乘法,即通过最小化PI模型计算位移和实际位移间的误差来辨识9个权重系数q值。模型辨识结果如表2所示。

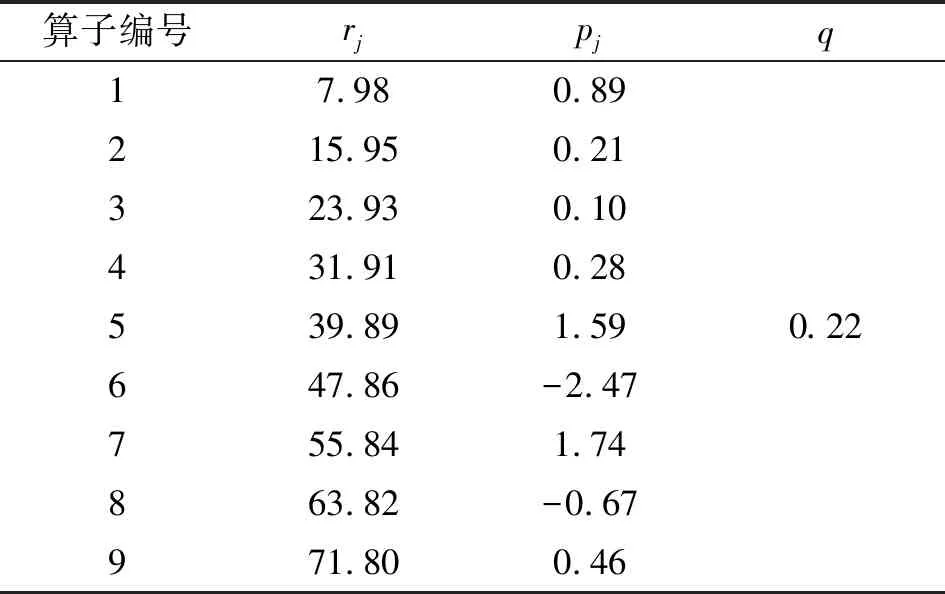
表2 PI模型辨识结果

4 实验结果分析

本文使用3种准确性的指标来对模型预测结果进行评估,分别是均方根误差(ERMS)、ERMS在观测值范围内的位置(ENRMS)和最大绝对误差(EMA)。

EMA表示预测值和观测值之间绝对误差的最大值。计算方法如下:

(i=1,2,…,N)

(17)

ERMS表示预测值和观测值之间差异(称为残差)的样本标准差。计算方法如下:

(i=1,2,…,N)

(18)

ENRMS表示ERMS在观测值范围内的位置:

(19)

由实验结果可知:

1) 由PI模型的预测误差结果(见表3)可知,经典PI模型对于该执行器的迟滞仍具有较好的静态建模能力。虽然最大绝对误差(EMA)值仍有6.50 μm,但是误差保证在[-5,+5]内,误差对称,ENRMS仅为2.15%。图8为对用于模型识别的5 Hz正弦波所对应的位移迟滞预测结果。

表3 PI模型的位移预测误差

图8 PI模型5 Hz正弦波位移预测

2) PI模型动态预测能力很差,对于9 Hz信号ENRMS已达2.34%。对于1 Hz信号预测(见图9)ENRMS误差已超过3%,很难达到工业上的精度要求。对于同频率衰减正弦波预测误差更大,EMA已达10.95 μm,模型预测基本失效。

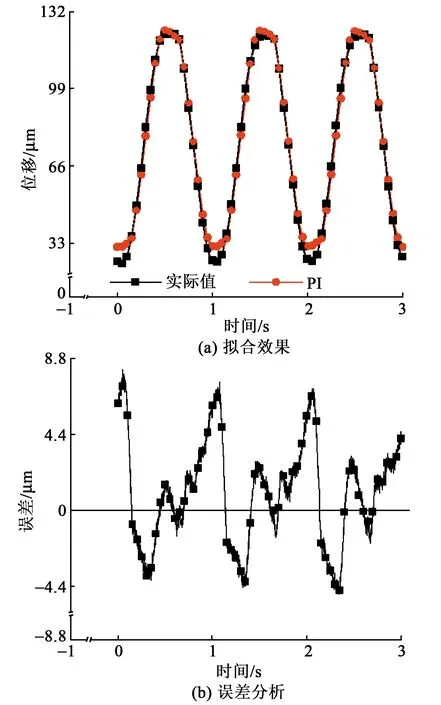
图9 PI模型1 Hz正弦波位移预测

将上述的经典PI模型作为对照组,由LSTM正弦波和衰减正弦波实验预测误差(见表4、5)可知,LSTM神经网络模型具有广泛的动态预测能力。

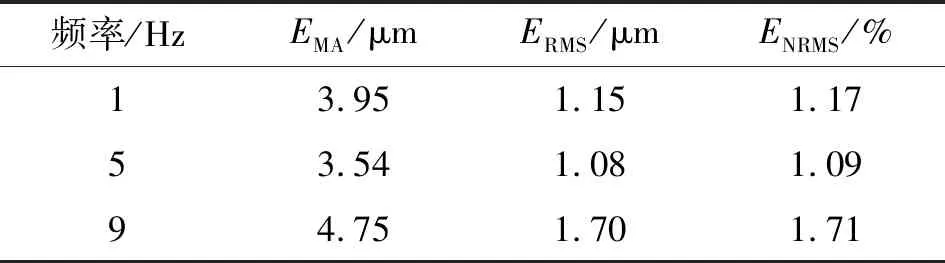
表4 LSTM神经网络正弦波预测误差

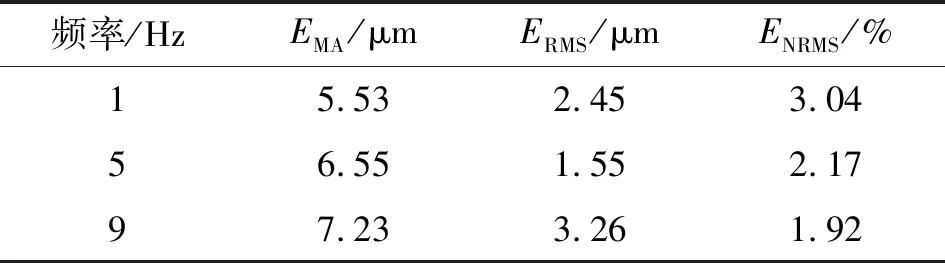
表5 LSTM神经网络衰减正弦波预测误差

3) 对于多频率正弦波信号,神经网络的最大绝对误差可以保证在±5 μm内基本上可满足LED测试要求。ENRMS可控制在2%内,精度较高。LSTM模型对5 Hz正弦波激励位移预测如图10所示。

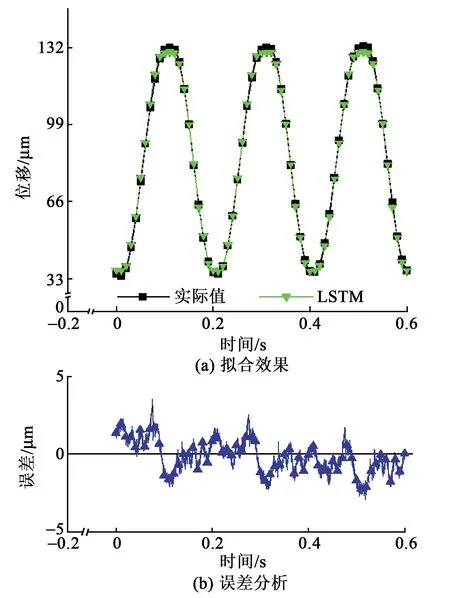
图10 LSTM模型5 Hz正弦波位移预测

4) 对于衰减系数τ=0.15的各频率衰减正弦波迟滞,ENRMS基本保证在3%内,说明神经网络不仅对正弦波具有动态建模能力,对于其他波形同样具有良好的预测能力。LSTM模型对5 Hz衰减正弦波激励位移预测如图11所示。

图11 LSTM模型5 Hz衰减正弦波位移预测

5 结束语

本文为了提高压电执行器的定位精度,分别使用经典PI模型和LSTM神经网络对其静态和动态迟滞进行建模。使用数据采集卡同时采集压电执行器的驱动电压控制信号和位移信号,从而获取压电执行器的多频率正弦波和衰减正弦波的迟滞数据。设计了一种由3层LSTM层和1层全连接层构成LSTM神经网络迟滞模型,使用GPU加速,通过80轮迭代,通过已获取的迟滞数据计算神经网络参数,并对经典PI模型参数进行识别。最后分别考察两种迟滞模型的位移预测效果,发现传统PI模型对于静态迟滞有较好的建模效果,动态效果较差,对于衰减正弦波的建模基本失效。以PI模型作对照组,LSTM模型不仅在动态迟滞建模方面具有优良的性能,整体误差保证在2%内,而且对于衰减正弦波同样可获得较良好的建模效果,基本上可达到工业应用要求。通过对压电执行器的迟滞效应进行有效建模,可以为LED晶圆检测提供一种更加高效的方法。