Sensitivity analysis and probability modelling of the structural response of a single-layer reticulated dome subjected to an external blast loading

Sho-bo Qi ,Gung-yn Hung ,d,* ,Xu-dong Zhi ,Feng Fn

a State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing,100081, PR China

b Key Lab of Structure Dynamic Behaviour and Control of the Ministry of Education, Harbin Institute of Technology, Harbin,150090, China

c Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters of Ministry of Industry and Information Technology, Harbin Institute of Technology, Harbin,150090, China

d Beijing Institute of Technology Chongqing Innovation Center, Chongqing, 401120, China

Keywords: Dome structure Blast load uncertainty Sensitivity analysis Probabilistic investigation Reliability evaluation

ABSTRACT The structural response of a single-layer reticulated dome to external explosions is shaped by many variables,and the associated uncertainties imply non-deterministic results.Existing deterministic methods for predicting the consequences of specific explosions do not account for these uncertainties.Therefore,the impact of the uncertainties associated with these input variables on the structures’response needs to be studied and quantified.In this study,a parametric uncertainty analysis was conducted first.Then,local and global sensitivity analyses were carried out to identify the drivers of the structural dynamic response.A probabilistic structural response model was established based on sensitive variables and a reasonable sample size.Furthermore,some deterministic empirical methods for explosion-resistance design,including the plane blast load model of CONWEP,the curved blast load model under the 50% assurance level,and the 20% mass-increased method,were used for evaluating their reliability.The results of the analyses revealed that the structural response of a single-layer reticulated dome to an external blast loading is lognormally distributed.Evidently,the MB0.5 method based on the curved reflector load model yielded results with a relatively stable assurance rate and reliability,but CONWEP did not;thus,the 1.2MB0.5 method can be used for making high-confidence simple predictions.In addition,the results indicated that the structural response is very sensitive to the explosion parameters.Based on these results,it is suggested that for explosion proofing,setting up a defensive barrier is more effective than structural strengthening.

1.Introduction

Single-layer reticulated domes (SRDs) are among the most common types of long-span spatial structures [1].Owing to their advantages of long span,light weight,and assembly convenience,these structures are extensively used in hangars,shipyards,and large-scale public buildings,such as the National Center for the Performing Arts in China that was built in 2001 and the Nagoya Dome in Japan that was built in 1997.These buildings,as symbolic buildings of social or economic importance in a country or region,often host large-scale events and receive thousands of visitors every day,making the buildings vulnerable to terrorist attacks.Following an explosion,different types of damages and even collapse-related failures may occur in SRDs [2-4].This study proposes a method for predicting the structural response of an SRD subjected to an external blast loading and provides practical protection suggestions.

In structural reliability analysis [5,6],various uncertainties are associated with the blast loading and structural property parameters,making it difficult to accurately predict the structural response of SRDs to explosions.The influence of uncertainties associated with blast loadings and structural properties on structural response requires deeper studies.Based on the statistics presented by Kingery et al.[7],the recorded field data of air-blast parameters exhibit certain discrepancies across different studies,even under apparently similar test conditions.UFC-3-340-02(Unified Facilities Criteria,2008) [6]usually takes the average as the standard value and provides it to designers.However,considering the explosion profile,Wu et al.[8,9]investigated the differences between the blast loads induced by spherical-and cylindrical-shaped charges,and found that UFC-3-340-02 predicted significantly lower axially oriented cylindrical charges,and also underestimated the radially oriented cylinder.In addition,considering different explosion types,Bogosian et al.[10]investigated 190 blast tests involving TNT,C-4 and ANFO explosives,and reported a 6%error in the mean value and a coefficient of variation of 0.23 for the reflected pressure.Thus,UFC-3-340-02 also proposes that the incident and reflected blast loads depend on the explosive's shape and type,detonator location,field conditions and other factors.Considering the inherent variability of blast loads,based on a small sample of one detonation of a general purpose (GP) 500-lb bomb and three detonations of GP 1000-lb bombs in free air,Twisdale et al.[11]reported a coefficient of variation of 0.30 for the incident overpressure and of 0.25 for impulses.With regard to the reflected overpressure,Campidelli et al.[12,13]observed that the coefficient of variation can reach 0.5,based on the reflected-overpressure experimental results of 90 studies,for data collected from full-scale steel,reinforced concrete,and masonry targets.Furthermore,Netherton et al.[14,15]and Stewart [16]carried out repetitive explosive field trials using 32 detonation types and obtained over 224 recorded pressure-time traces.Using a large database,considering the variability of the explosive mass,net equivalent quantity,stand-off distance,angle of incidence,air temperature,pressure and model error,a probabilistic blast load model at different scaled distances was developed,conforming to a normal distribution.In addition,Qi et al.[17-19]carried out a series of repeated field trials for investigating the variability associated with reflected blast loadings on the dome structure.Their study demonstrated that the variability of each blast load parameter with respect to the dome structure decreases with increasing scaled distance and follows a normal distribution.Regarding the effect of the load variability on the structural response,Kelliher et al.[20]considered the explosive's location,magnitude and duration,as well as the building-imposed loading as random variables,and performed a statistical analysis showing that the fractional damage of concrete-framed buildings owing to explosions is Weibull-distributed.In addition,inherent to every structure are the uncertainties associated with its material and dimensions[21].Hao et al.[22]computed the probability of the RC column blast load-induced failure,assuming that the column dimensions,reinforcement ratio and material strength are normally distributed,and so is the blast load.Compared with deterministic blast loadings and/or column properties,different response modes were obtained by considering random variations,which further indicated the importance of accounting for uncertainties when assessing the blast load effects on structures.Related structural component analysis [23-30]also indicated that the variability associated with external and intrinsic factors can result in the blast load uncertainty under certain conditions,and this should be considered in reliability-based designs.With regard to bombingrelated terrorist attacks,explosion points and explosive quantities cannot be accurately predicted or estimated;combined with the inherent variability of blast loads this results in very complex loading conditions.Moreover,when manufacturing a structure,it is also very difficult to ensure sufficiently predefined accuracy,even for well-made steel structures,because material properties can change in the process of production and manufacturing.Thus,there remain many questions regarding the response characteristics of SRDs to explosions in the presence of numerous uncertainties.

Much work has been done on the modelling of SRDs subjected to explosions[2-4];repetitive experiments on external blast loads along dome structures were conducted as well [17-19].The present study focuses on the sensitivity analysis and probability modelling of the structural response of an SRD subjected to an external explosion.First,the sources of uncertainty are analysed,including the blast load variables and structural property variables.Some current deterministic methods and ideas are also introduced.Then,local and global sensitivity analyses are conducted,for capturing the dominant factors determining the structural dynamic response.Finally,a probabilistic structural response model is established,and deterministic methods for explosion-resistance design are used,for the reliability evaluation.

2.Parametric uncertainty analysis

2.1. Blast load variables

According to the statistical analysis and repetitive explosion test results [15-19],the uncertainties associated with a blast load on a dome-shaped structure mainly include the TNT equivalent(W),the nearest distance between the explosive and the structure (R) and the inevitable uncertainties of the blast load(η),as listed in Table 1.Previous studies [14,15]suggested that the TNT quantity and detonation distance follow a normal distribution,with the coefficients of variation of 0.102 and 0.1,respectively,for a vehiclemounted improvised explosive device (VBIED) detected by the global positioning system(GPS).

Table 1 Probabilistic statistical models of structural parameters.

The mean values of positive impulse (Ir) and overpressure (Pr)can be obtained using the semi-empirical Eq.(1)-Eq.(6) [17-19].

whereMean(MEIr)andMean(MEPr)are coefficient of correction,θ is the structural angle between the point on the structural surface and the horizontal plane of the lower edge of curved structure.aIr,bIr,cIr,aPr,bPr,cPrare the structure's shape parameters.Mean(MEIr) andMean(MEPr) are be calculated using Eq.(3) and Eq.(4)

where andZis the nominal scaled distance,calculated using Eq.(5).

aIr,bIr,cIr,aPr,bPr,cPrcan be represented byyand are given by Eq.(6),

as follows:

The parameterHis the supporting height of the SRD,the parametersAy,By,Cy,Dy,andEy,are the fit constants for the shape parameter (y),and their values are listed in Table 2.

Table 2 The blast load model parameters [17-19].

Table 3 Global sensitivity analysis of vertex displacement.

In addition,repeatable explosive field trials on a dome demonstrated that the blast load parametersIrandPrfollow a normal distribution.The coefficients of variation(COV)forIrandPrare given in Eq.(7) and Eq.(8) [19].

2.2. Structural property variables

Owing to the influence of the manufacturing accuracy of structural members and continuous changes of the SRD environment,the factors affecting the uncertainty of structural properties mainly include the randomness of structural parameters,such as the material yield strength(fy),elastic modulus(E),roof quality(Pm)and member cross-sectional area (A).Q235 steel was selected for the SRD in this study.Many statistical studies[31]showed that the yield strength of Q235 steel follows a normal distribution,with a mean of 251 MPa and a coefficient of variation of 0.081.According to the steel structure design code[31],the elastic modulus of Q235 steel is 206 GPa.The international joint committee on structural safety (JCSS) [32]recommends to use a lognormal distribution for modelling the elastic modulus of Q235 steel,with a coefficient of variation of 0.03.A roof with an area density of 120 kg/m2[33]was selected for the modelled SRD in this study,and the roof dead load obeyed a normal distribution,according to the unified standard for the reliability design of building structures (GB50068-2001) [34];the coefficient of variation was set to 0.07.Based on the member stability requirements for SRDs,the specifications of the radial and circular members were Φ194 × 6 (Φ steel tube,outer diameter in mm × thickness in mm)steel pipes (average cross-sectional area,3.5 × 10-3m2),while the diagonal members adopted the specification of the Φ168 × 6 (Φ steel tube,outer diameter in mm × thickness in mm)steel pipe (average cross-sectional area,3.1 × 10-3m2).The members’ cross-sectional area followed a lognormal distribution,with a coefficient of variation of 0.02.The uncertainties of the related structural parameters are listed in Table 2.

3.Finite element modelling of the SRD

3.1. SRD configuration

A typical configuration of an SRD subjected to an external explosion is shown in Fig.1 and Fig.2.A single-layer Kiewit 8 SRD(span,60 m;rise-span,1/7)was considered,as shown in Fig.1.The SRD was built on a supporting wall(height,5 m),and a TNT charge(mass,1000 kg)was placed on the ground 20 m away from the SRD.

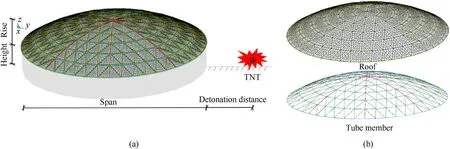
Fig.1.(a) Configuration of the SRD subjected to an external explosion and (b) its structural elements.

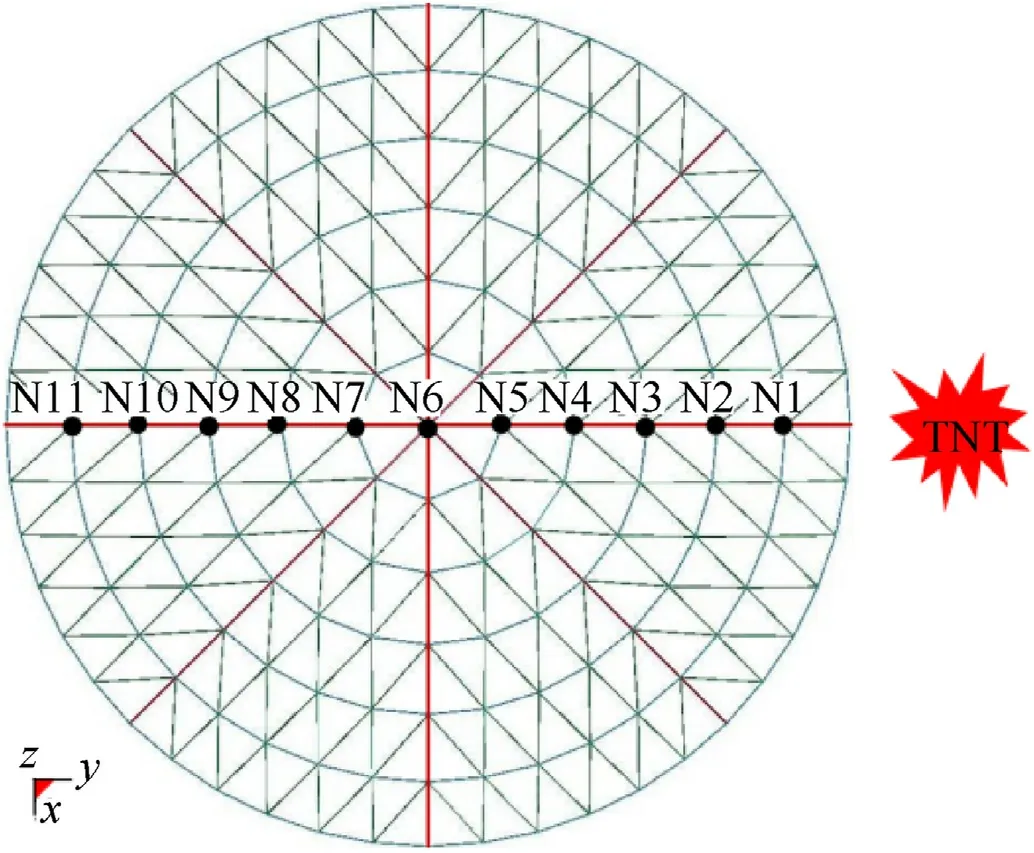
Fig.2.Top view and gauges on joints along the SRD.

An SRD structure with six rings,built using ANSYS/LS-DYNA[35],is shown in Fig.1.All the tube members in the dome structure were delicately simulated using the beam161 element.The roof panel was simulated using the shell 163 element.All of the members were divided into six beam elements along the length direction.The mesh size of the roof panel was generally consistent with those of the members.Nodes were shared,and the contact forces were transferred to the intersecting grids.The automatic contact type of the keyword *CONTACT_AUTOMATIC_GENERAL was used to automatically handle the contact between shell to beam element.In addition,the SRD model was constrained by three-way fixed hinges on a support.The support was simplified as a rigid target without deformation.To represent the dynamic mechanical behaviour of mild steel,the Cowper-Symonds constitutive model was adopted,which is especially useful to model strain rate effect.This modelling method has been verified by experiments [2-4]for further study.

3.2. Empirical blast loading models

CONWEP load model:In anti-explosion design and capacity evaluation of structures,empirical blast loads based on CONWEP[36]are widely used in plane reflection structures.The pressure acting at any point on the target is a function of the reflected pressure and incident pressure at that point,and the angle of incidence of the blast wave α,

wherepiis the incident pressure andpris the reflected pressure.

MB0.5 load model:Based on the probability model of the blast load on a curved surface,a 50% assurance level of the empirical blast load model (MB0.5) based on Eq.(1)-Eq.(6) can be used for curved reflection structures,especially for the SRD in this study.

1.2MB0.5 load model:Previous studies [2,5,6,11-13,19-30]suggested that the variability of blast loads significantly affects the structural dynamic response.Therefore,it was recommended to increase the design TNT equivalent by 20% in the design manual UFC-3-340-02 [6],to avoid overestimating the structural bearing capacity with respect to explosions.That is,increasing the TNT equivalent 1.2-fold was suggested,to account for the influence of all uncertainties,to ensure the structural reliability design.Thus,Eq.(5)and Eq.(6)should be accordingly revised as Eq.(10)and Eq.(11),

In a strict sense,the above three anti-explosion design ideas and methods correspond to deterministic loading methods,without any specific consideration of the variability associated with various input parameters.

4.Sensitivity analysis of structural dynamic response

4.1. Local sensitivity analysis

Considering that there are many explosions and structural parameters affecting the structural dynamic response behaviour,a local sensitivity analysis was first carried out,for quantifying the degree of influence of various uncertainty factors.Based on Eq.(12),the influence of major factors on the structural response is preliminarily discussed and identified,using the following definition of sensitivity:

whereSLiis the local sensitivity of thei-th input parameter (with input parameters including the TNT equivalent(W),the detonation distance(R),inevitable uncertainties associated with the blast load(η),the yield strength of the steel pipe (fy),the elastic modulus of the steel pipe (E),the roof load (Pm) and the member section area(A));yis the mean structural response (with the response metrics such as the structural plastic member ratio (nP),structural vertex displacement (Dver),overall maximal structural displacement(Dmax) and overall average strain (εa));and Δyiis the size of the 16%-84%quantile of thei-th parameter,with the other parameters assuming their corresponding mean values.

The results of the local sensitivity analysis in Fig.3 show that the TNT equivalent (W),the detonation distance (R),the inevitable uncertainties associated with the blast load (η) and the member section area (A) significantly affect the structural response.The sensitivity decreases,but the uncertainty of other parameters relatively weakly affects the structural dynamic response to an external explosion.

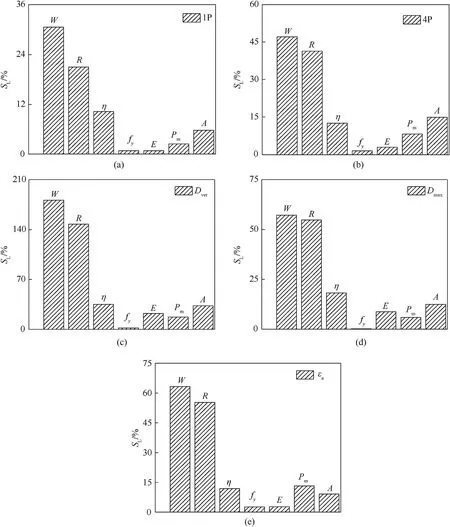
Fig.3.Local sensitivity response diagram:(a)Plastic ratio of the member of 1P;(b)Plastic ratio of the member of 4P;(c)Vertex displacement;(d)Maximal displacement;(e)Mean plastic strain of member.

4.2. Global sensitivity analysis

Based on the local sensitivity analysis results,only the TNT equivalent (W),the detonation distance (R),the inevitable uncertainties associated with the blast load (η) and the member section area (A) were further considered in the global sensitivity analysis of the SRD's dynamic response.In this study,the Latin hypercube sampling(LHS)method[37]was used for near-random sampling of these four high-sensitivity parameters.To select reasonable sampling times and ensure the reliability of the analysis results,a convergence analysis of the sample size was carried out first.The mean and the standard deviation of the structural response indexes for different sample sizes were counted,as shown in Fig.4.It can be observed from Fig.4 that when the sample size is greater than 250,the mean value and the standard deviation of the 1P member plastic ratio and maximal node displacement begin to stabilise.Therefore,300 samples were used for investigating the global sensitivity of the SRD subjected to an external explosion.

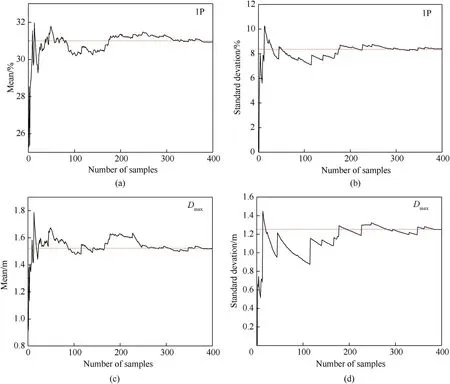
Fig.4.Relationship between the SRD statistical response and sample size:(a)Mean of 1P;(b)Standard deviation of 1P;(c)Mean of maximal displacement;(d)Standard deviation of maximal displacement.

Next,Sobol's sensitivity analysis was carried out for determining the transfer regularity and contribution rate of the uncertainties associated with high-sensitivity input parameters to structural response.Tables 3-7 list the first-order sensitivity and total sensitivity results for the explosion parameters(W,Rand η)and the structural parameter (A) with respect to the structural response indexes,which include the vertex displacement,the maximal displacement,the 1P member plastic ratio,the 4P member plastic ratio and the average plastic strain.Macroscopically,the uncertainty contribution rate of the explosion parameters(W,R,η)ranges from 0.6%to 89.1%,while that of the structural parameter(A)ranges from 3.4% to 12.9%;thus,the uncertainties associated with the explosion parameters contribute more to the uncertainty of each response index than those of structural parameters.For a moreintuitive observation,the contribution rate of each variable to the structural response is shown in the pie chart in Fig.5.In particular,the dynamic response behaviour indexes of the structure,such as the vertex displacement,the maximal displacement,the member plastic ratio and the overall average plastic ratio,are more sensitive to the uncertainty of the TNT equivalent,with a contribution rate in the 65.8%-89.1% range.In addition,the maximal displacement response can represent the local response degree of the structure,that is,the local depression depth.Therefore,it can be concluded from Table 4 and Fig.5(b)that there is a smaller difference between the contribution rates of explosion parameters and structural parameters to the local depression,compared with other structural response indexes.It was also found that the first-order sensitivity and total sensitivity of the TNT equivalent and detonation distance are quite different for various response indexes.That is because the first-order sensitivity reflects the influence degree of the uncertainty of a single parameter,while the total sensitivity reflects the interactive comprehensive influence degree of the uncertainty of multiple parameter variables,and these two explosion parameters also somewhat affect the inevitable uncertainties associated with the blast load,suggesting an interaction between the various factors of an explosion load.

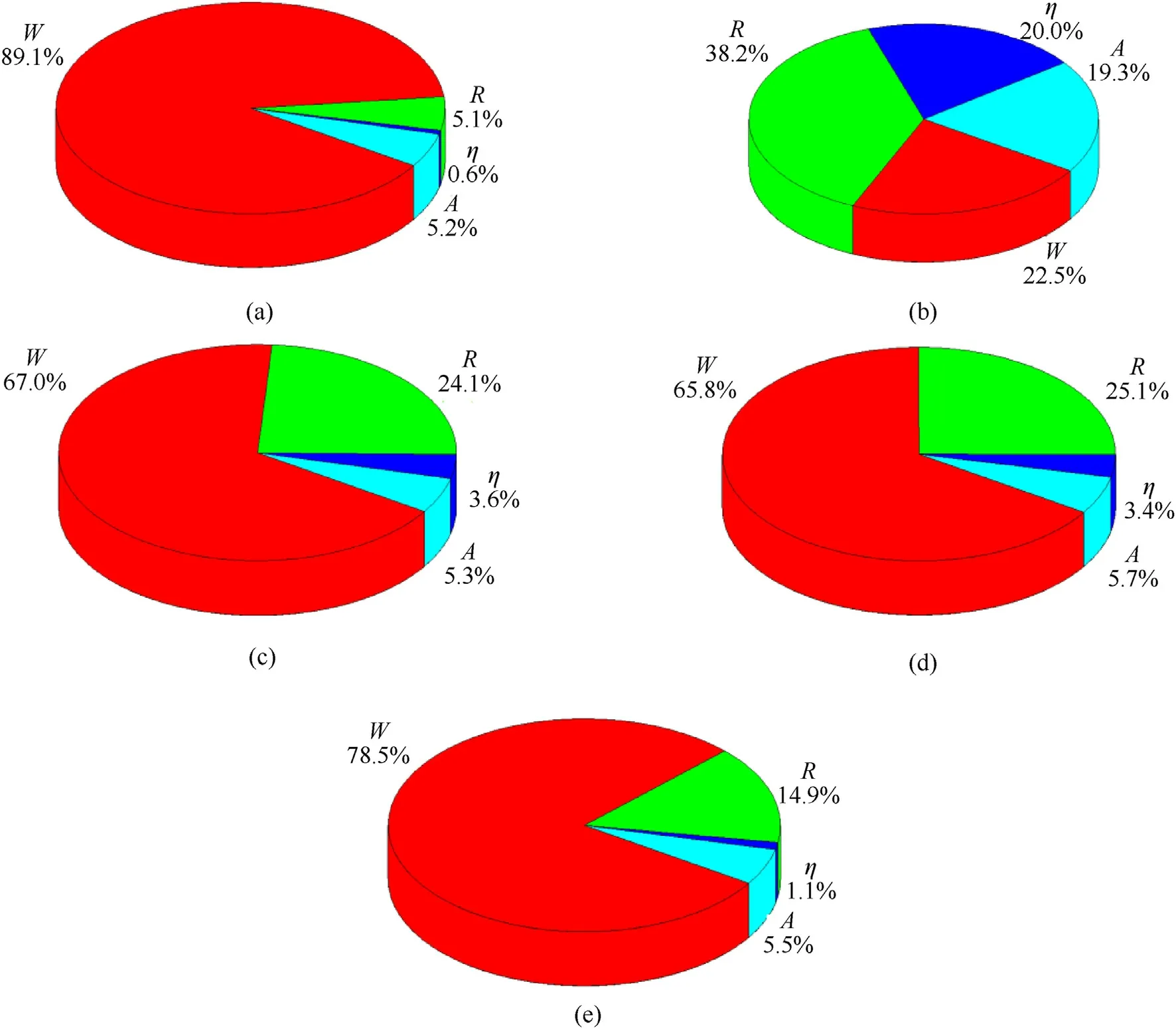
Fig.5.Total sensitivity of response,with respect to different stochastic factors: (a) Vertex displacement;(b) Maximal displacement;(c) Ratio of yielding members under 1P;(d)Ratio of yielding members under 4P;(e) Mean plastic strain of member.

Table 4 Global sensitivity analysis of maximal displacement.

Table 5 Global sensitivity analysis of 1P.

Table 6 Global sensitivity analysis of 4P.

Table 7 Global sensitivity analysis of the average plastic strain.

5.Probability modelling and reliability evaluation of empirical methods

5.1. Probabilistic structural response model

Based on the sensitivity analysis results,the variability of the TNT equivalent,detonation distance,inevitable uncertainties associated with the blast load and member section area should be prioritised when considering the variability of the dynamic response of the SRD to an external explosion.To establish a probabilistic structural response model,some less sensitive parameters,such as the structural material yield strength,elastic modulus and roof quality,were regarded as deterministic parameters in the following,allowing to simplify calculations.

According to previous studies on the collapse failure mechanism,the response index limits can be set as follows: the vertex displacement is 1/100 of the rise,the maximal displacement is 1/20 of the span,65% of the members in the structure enter the yield stage,30%of the members develop full-section depth plasticity and the average plastic strain of the members is 0.013 times the ultimate plastic strain.Therefore,when the ratio of the response index to the failure limit is above 1,the corresponding structure enters the failure mode.According to the statistical results in Fig.6,three working conditions for our 300 considered numerical examples induced failures;the failure probability of an SRD with an 80 m span and subjected to a 100 kg TNT explosion at a 20 m distance was 1%.

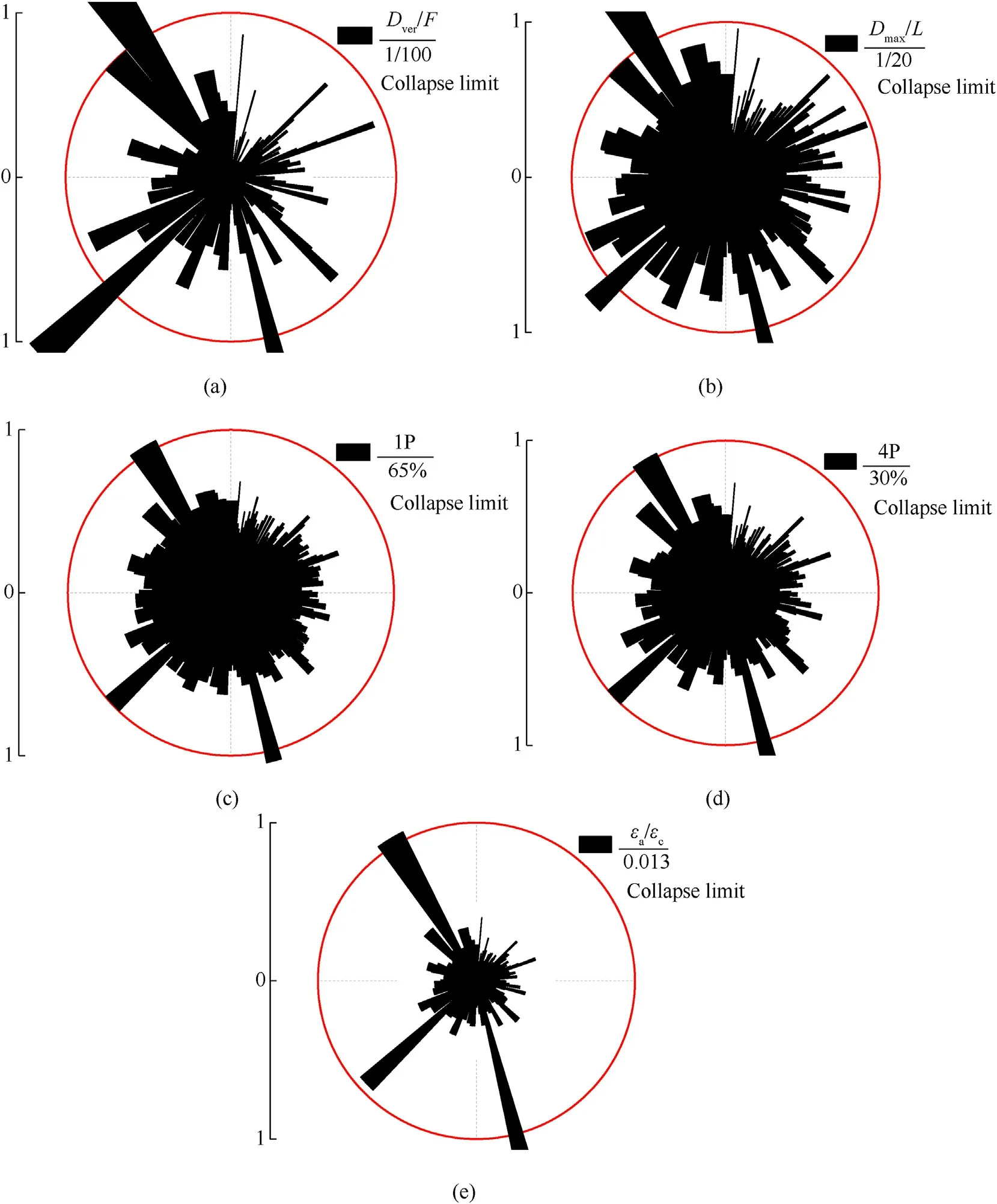
Fig.6.Failure limit statistics for different response indexes,for the modelled SRD: (a) Vertex displacement-rise ratio;(b) Maximum displacement-span ratio;(c) Ratio of yielding members under 1P;(d) Ratio of yielding members under 4P;(e) Ratio of Mean plastic strain of members.

Based on the response index samples for the SRD,the response probability distribution characteristics can be obtained,and the response probability distribution model can also be established.Many probability distribution models could be selected to yield the desired distribution characteristics,such as the normal distribution,the lognormal distribution,the Weibull distribution,the Gumbel distribution,the gamma distribution and the Rayleigh distribution.A Kolmogorov-Smirnov (K-S) test indicated that only the lognormal distribution was acceptable at the 5% significance level for describing the structural response characteristics,such as the proportion of structural plastic members (nP),structural vertex displacement(Dver),maximal displacement(Dmax),overall average strain of a member(εa)and rib joint displacement along the YZ rib joints of the SRD structure(gauges N1-N11),as shown in Fig.6.The goodness-of-fit method was further used for calculating the goodness of each response index assuming a lognormal distribution.The test results show that the goodness-of-fit for the lognormal distribution is above 0.9994,further suggesting that the probabilistic structural response model of the SRD structure is characterised by a lognormal distribution.

5.2. Reliability evaluation of empirical methods

The sensitivity analysis results suggested that the uncertainties associated with the blast load and structural characteristics significantly affect the dynamic response uncertainty of the SRD structure.Therefore,assuming reliability-based design [5,6],a structural response probabilistic model considering structural (A)and blast load (W,R,η) uncertainties should be established,for obtaining the probability distribution characteristics and for evaluating the reliability of deterministic load methods.Deterministic load models,including the most commonly used blast model(CONWEP),the curved blast load model under the 50% assurance level (MB0.5) and the 20% mass-increased method (1.2MB0.5),were used,for evaluating the reliability of the structural response predictions.In addition to the proportion of structural plastic members (nP),the structural vertex displacement (Dver),maximal displacement(Dmax),overall average strain of a member(εa)and rib joint displacement along the YZ rib joints of the SRD system(gauges N1-N11) were considered for establishing the probability model.

Fig.7 shows the displacement distribution results for each point on the YZ main rib,and it is observed that the average displacement for N1 is 1.36 m,the 50th percentile of the displacement for N1 is 1.50 m,the range of the displacement for N1 is 5.02 m;the average displacement for N3 is 0.63 m,the 50th percentile of the displacement for N3 is 0.73 m,the range of the displacement for N3 is 10.73 m;the average displacement for N3 is 0.63 m,the 50th percentile of the displacement for N3 is 0.73 m,the range of the displacement for N3 is 10.73 m;the average displacement for N6 is 0.19 m,the 50th percentile of the displacement for N3 is 0.23 m,the range of the displacement for N3 is 7.22 m.The farther away from the detonation,the smaller the average displacement and the 5-95th percentile displacement difference.However,the range of the joint displacement first increases and then decreases with an increase in the detonation distance.In addition,the data tail is longer in the right half than in the left half.The joint displacement distribution of each node exhibits obvious right-deviation distribution characteristics.

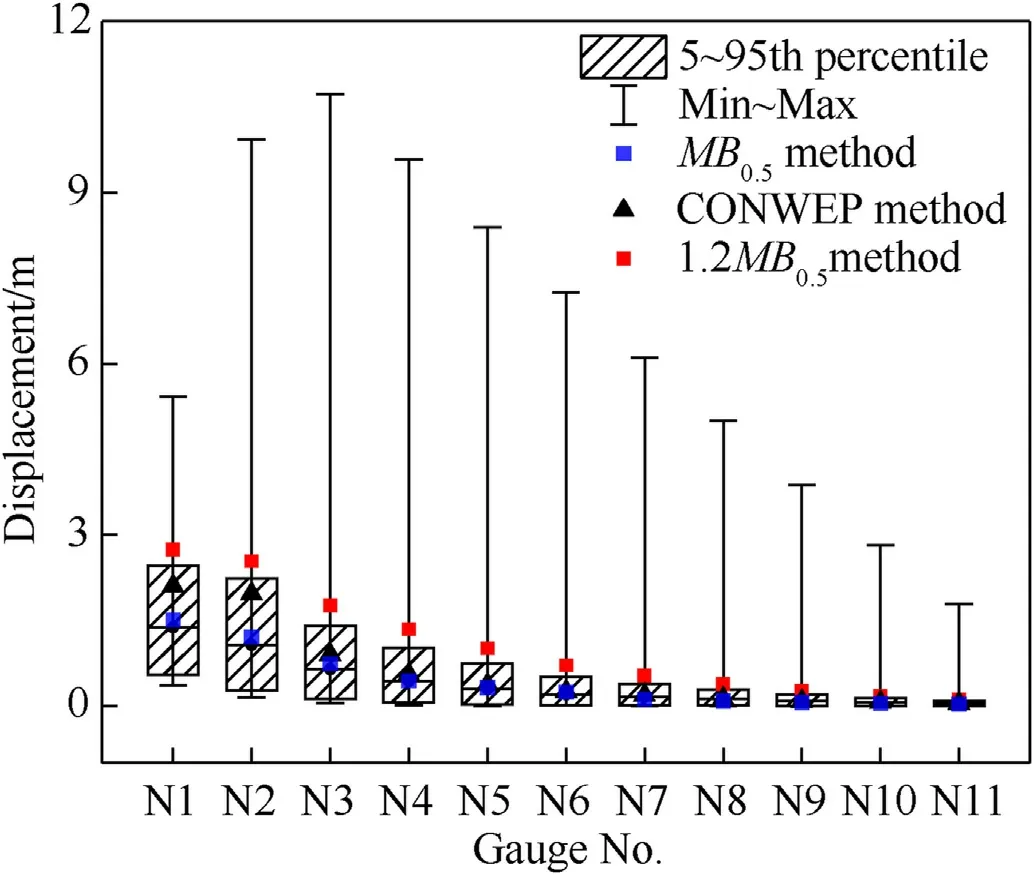
Fig.7.Displacement results for the YZ rib of the structure.

Meanwhile,the displacement results for the 1.2MB0.5and CONWEP methods were basically in the upper quantile range,and their assurance rates were 93%-96% and 70%-90%,respectively,while the assurance rate of theMB0.5method for these sample data was 53%-59%,as shown in Fig.8.It should be noted that the assurance rate refers to the cumulative distribution function.Considering the probability distribution of the member plasticity under 1P in Fig.9,the mean was 30.4%,and the coefficient of variation was 0.21.The member plasticity results for the 1.2MB0.5,CONWEP andMB0.5methods were 43.9%,44.7% and 30.7%,and their assurance rates were 96%,97% and 52%,respectively.Furthermore,the assurance rates of the proportions of the structural plastic members (nP),structural vertex displacement (Dver),maximal displacement(Dmax)and overall average strain of member(εa)are shown in Fig.10.The assurance rates of each response index based on the 1.2MB0.5,CONWEP andMB0.5methods were 92%-97%,78%-97% and 50%-59%,respectively.The sensitivity analysis indicated that the SRD's response was more sensitive to the uncertainty of the TNT equivalent;therefore,the 1.2MB0.5method can provide relatively consistent response results but with a high and stable assurance rate.In the actual design,this method can be used for making simple yet high-confidence predictions.Although the response results for the CONWEP method were in the upper quantile interval,the variation in the assurance rate could reach 19%;thus,stable predictions cannot be guaranteed.Conversely,theMB0.5method can provide an approximate median response solution.

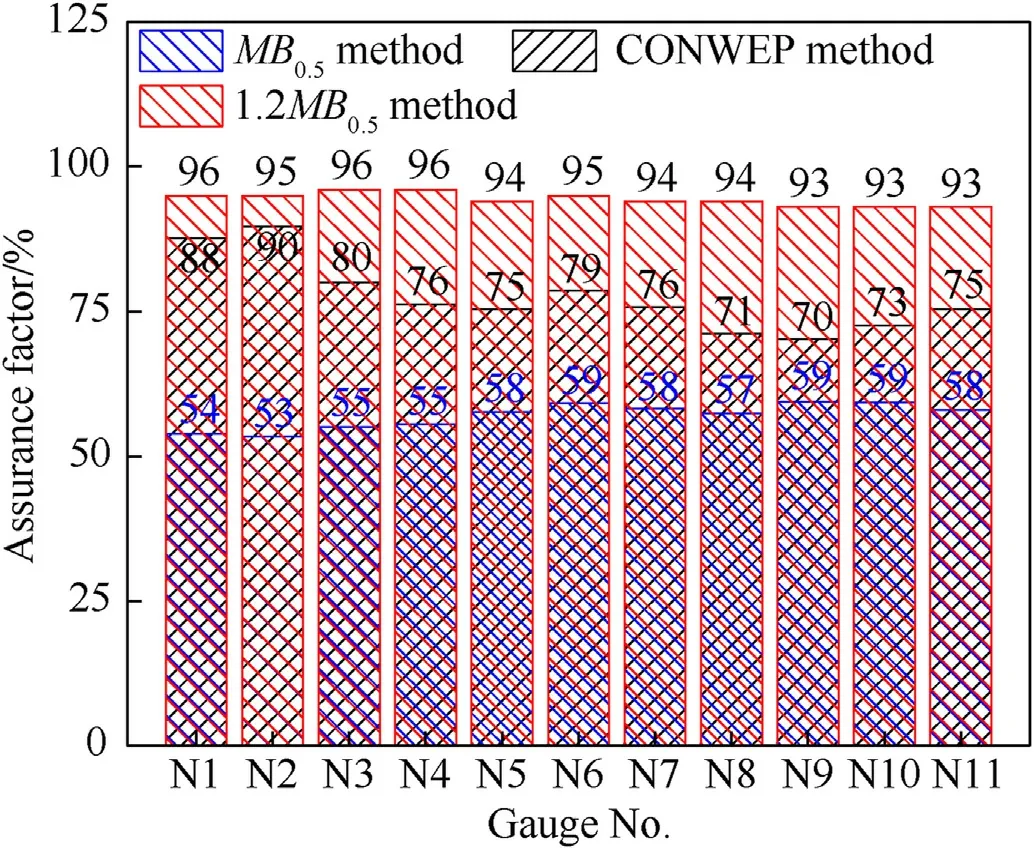
Fig.8.Assurance factors of the displacement response for the YZ rib of the structure.

Fig.9.Probability distribution for ratios of yielding members under 1P.

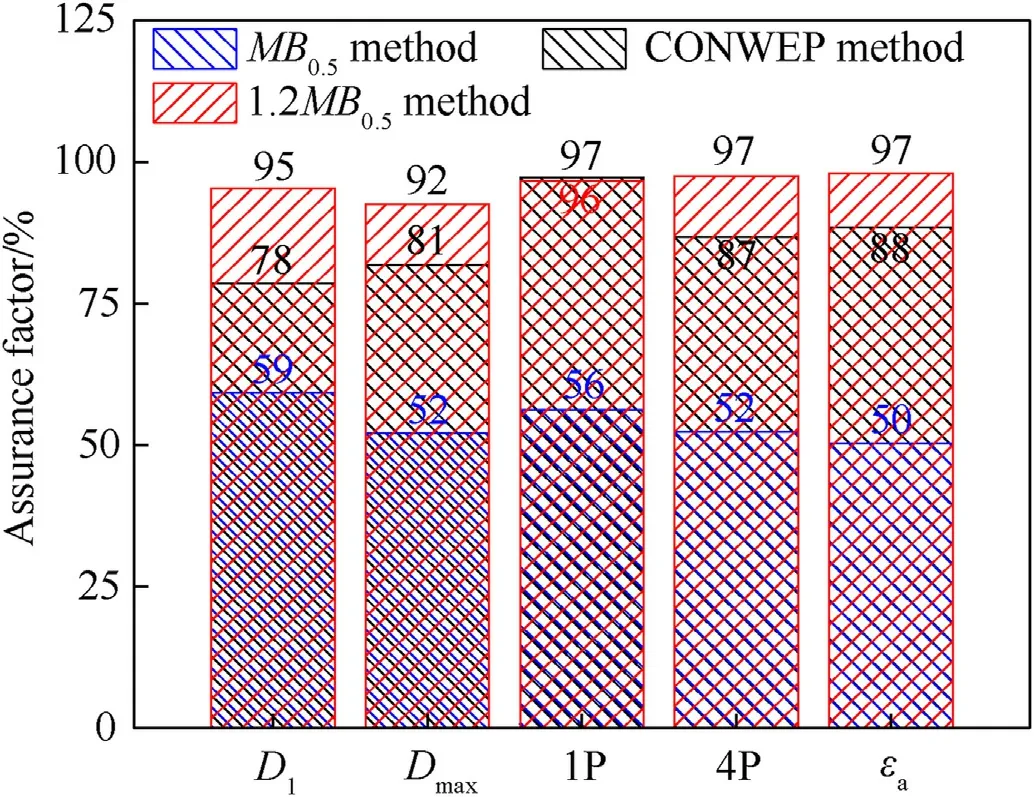
Fig.10.Assurance factors,for each response index of the structure.

6.Conclusions

The main goal of this study was to investigate the probabilistic distribution of the dynamic response of an SRD structure subjected to an external blast loading.Thus,parametric uncertainty and sensitivity analyses were conducted,for capturing the dominant factors of the SRD's structural dynamic response.A probabilistic structural response model was then established,and deterministic empirical methods for explosion-resistance design,including the most commonly used blast model(CONWEP),the curved blast load model under the 50% assurance level (MB0.5) and the 20% massincreased method (1.2MB0.5),were considered for evaluating the predictions'reliability.The conclusions of this study are as follows.

(1) The sensitivity analysis demonstrated that explosion parameters including the TNT equivalent (W),detonation performance (R),inevitable uncertainties associated with the blast load (η) significantly affect the structural response of the SRD structure to an external explosion.For a given structure,it is suggested that setting up a defensive barrier is more effective than strengthening structural materials by explosion-proof treatments,such as bollards and blast walls.

(2) This study yielded the probability distribution of the SRD's response to a given explosion,for an SRD with given structural properties.The probability distribution of the dynamic response exhibited obvious right-deviation distribution characteristics.By comparing the computed statistics for the fitted trial probability distribution functions and those for the data,it was evident that the dynamic response of the SRD under an external explosion is likely lognormally distributed.In addition,the dispersion of the dynamic response throughout the entire structure space first increased and then decreased with increasing the detonation distance.

(3) The CONWEP method can provide a conservative proxy of the dynamic response model,but it lacks stability or a uniform assurance rate,which indicates that it is not suitable for predicting the dynamic responses of SRD structures.TheMB0.5method based on the curved reflector load model yields results with a relatively stable assurance rate,close to the median of the dynamic response probability model,which is adequate for calculating the dynamic responses of SRD structures.The 1.2MB0.5method yields relatively consistent responses,but with a high assurance rate.In the actual design,this method can be used for making simple yet high-confidence predictions.Overall,deterministic research methods may lead to an inaccurate design of structures,with poor blast load resistance and an inability to accurately assess structural performance in a given explosion scenario.

(4) The research findings herein serve as a foundation for further development of blast load model for solving dynamic response mechanism and evaluation study.Furthermore,it could be applied to optimize the explosion-proof treatments on the single-layer reticulated dome subjected to external blast loading.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors wish to thank the financial support from the China Postdoctora Science Foundation (project No.2021M690406) and also the financial supports from the National Natural Science Foundation of China (project Nos.51708521,51778183).