三维重构下整体形状参数的砂土渗透性分析

王志兵,翁峻择,孙广,马高峰,华天波

(1.桂林理工大学土木与建筑工程学院,广西 桂林 541004;2.广西岩土力学与工程重点实验室,广西 桂林 541004;3.中国五冶集团有限公司,四川 成都 610063)

0 引言

砂土是工程建设中一种重要材料,被广泛使用于土石坝、岛礁吹填等工程.渗透性作为砂土的一个重要工程特性,与许多工程的稳定性(滑坡、渗流)问题密切相关.砂土渗透特性受其孔隙结构、颗粒粒径分布、颗粒形状等因素的影响.目前,预测土体的渗透系数模型考虑的因素大多集中在颗粒大小及分布、孔隙度、孔隙连通性等参数,而对颗粒形状的关注偏少.如代表性的科泽尼-卡尔曼(Kozeny-Carman,K-C)方程,方程包含与土体结构相关的主要参数有孔隙率、孔隙形状系数、比表面积和曲折度等参数,然而在确定颗粒的比表面积参数时常常存在困难[1].比表面积的确定常用理论法[1]和试验法[2],但这些方法都存在一定的不足,如使用颗粒级配来估计颗粒的比表面积会简化颗粒形状的影响[3].

砂土的颗粒形状决定了土体的微观结构,进而决定了土的宏观物理特性[4-5],探索砂土的颗粒形状及微观结构对分析其渗透特性有重要作用.最早由Wadell等[6]提出了圆度来表征颗粒的棱角性、球度来表征颗粒的球形近似度,这引发了大量研究人员着手于颗粒形状的研究.Liu等[7]通过随机生成不同颗粒组成构造各不相同的多孔介质进行渗透模拟,发现颗粒形状和表面特征对渗透性有重要影响.任玉宾等[8]在二维层面上描述了3种形状砂土颗粒形状特征,探究了球度对于渗透系数的影响.Witt等[9]通过理论推导了颗粒平整度、方向与渗透率的相关性,引入了比表面积和流动路径的曲折度作为K-C方程的变量.Tickell等[10]通过一系列渗透试验探究了自然堆积的砂土中颗粒形状对于孔隙率以及渗透性的影响.

近年来,随着先进的微观测试手段和计算方法的发展,颗粒的微观特征对土体渗透性的影响越来越受到重视.通过高分辨计算机断层扫描(computed tomography,CT)技术无损重构土样的三维精细化结构,并通过图像处理后能得到丰富的土结构参数,被应用于岩土工程等相关领域的研究工作.刘清秉等[11]采用图像处理软件分析不同形状砂土的形状特征,统计了各形状参数的分布.Liang等[12]将CT扫描技术和球谐函数分析相结合,完成石英砂颗粒和钙质砂颗粒的精确三维重构.彭家奕等[13]通过CT三维重构不同颗粒形状粗粒土的孔隙结构特征,发现颗粒的形状越复杂,孔隙的比表面积越大,对应的渗透系数也越低.蔡沛臣等[14]通过探讨COMSOL与AVIZO联合仿真技术的可行性,为三维重构及渗流模拟提供了新技术.Indraratna等[15]提出一个包含颗粒形状信息的有效粒径值,引入到K-C方程可以预测不均匀系数高达20的粗粒土的饱和渗透系数.Nguyen等[3]通过高分辨CT计算了不同颗粒形状的砂土的形状参数,认为具有相同颗粒级配和相同孔隙率的砂土具有不同的渗透率,颗粒形状能显著影响砂土的渗透性.文献[16]通过砂土图像提出一个新的有效颗粒粒径表达式,修正了K-C方程用于预测砂土渗透系数.从上述文献可知,颗粒形状对砂土等颗粒材料的渗透系数具有重要影响,采用何种颗粒形状去精确表征其影响,学者们提出了多种不同的处理方法,但大部分研究采用单一形状参数,关于颗粒整体形状特征对砂土渗透性影响的研究较少.

本研究使用CT对玻璃珠、石英砂及玻璃渣3种颗粒级配相同但颗粒形状各异的砂土进行扫描;通过软件对采集的图像进行三维重构,分析砂土的微观结构特征,计算砂土的结构参数,选定适用于表征颗粒整体形状的颗粒整体形状参数(OR)引入K-C方程进行砂土渗透系数预测;最后采用柔性壁渗透试验测试不同颗粒形状砂土的渗透系数,验证所提出的考虑颗粒形状的预测砂土渗透系数的改进K-C方程.

1 试验方案

1.1 试验材料

使用石英砂、玻璃珠及玻璃渣3种材料,如图1所示,其中石英砂取自福建省非金属矿有限责任公司的灌砂法专用砂,二氧化硅的质量分数高达95%;玻璃珠和玻璃渣均为熔融石英砂,两者不同之处在于前者颗粒表面光滑、形状近似圆润球体,而后者颗粒多棱角、形状不规则,二者的二氧化硅质量分数均高达98%.可以认为,玻璃珠、玻璃渣和石英砂,物质组成相似但形状不同,且3种颗粒形状具有较强代表性,为后续研究提供可靠支撑.

图1 砂土颗粒图像

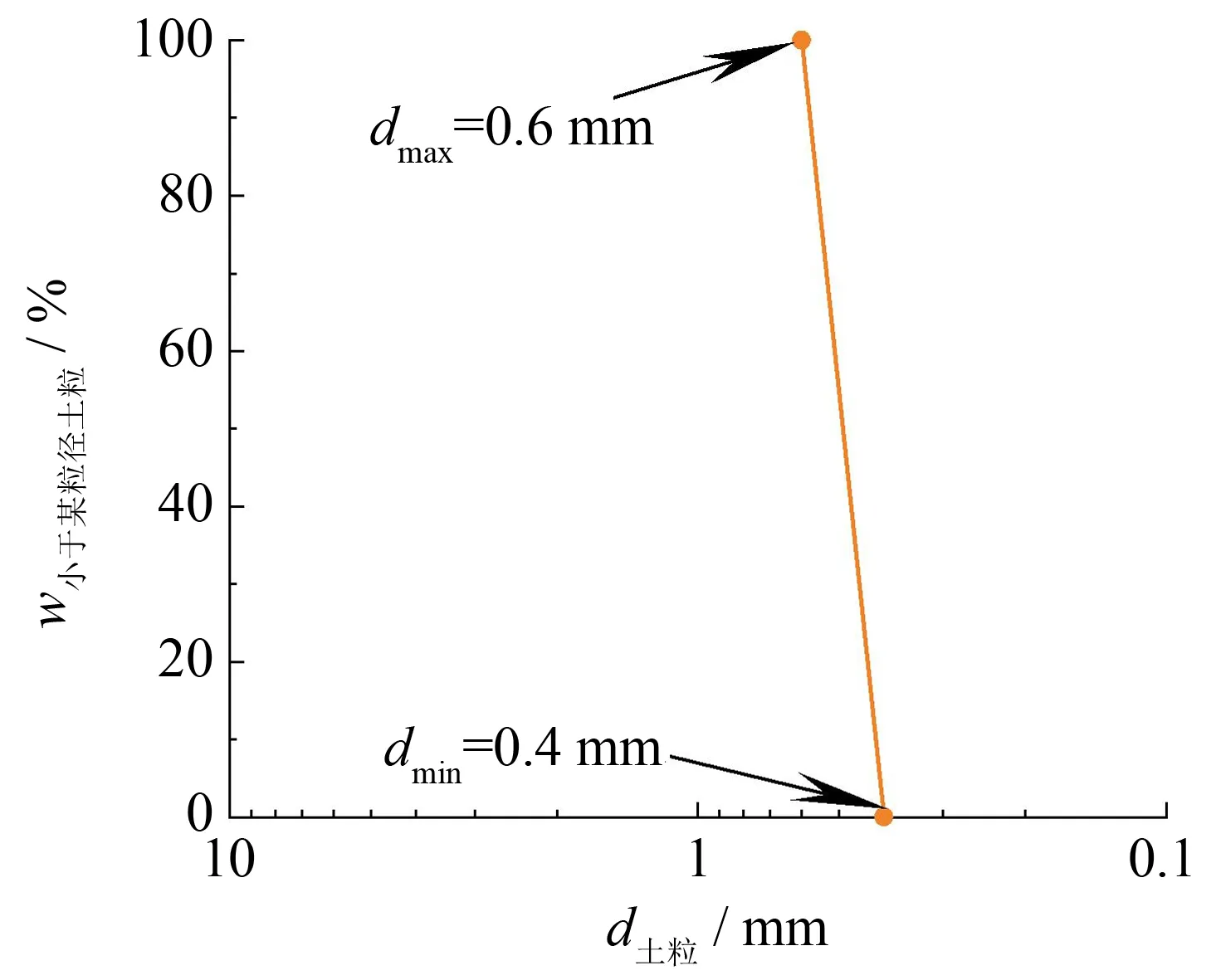
图2 砂土试样的颗粒级配曲线Fig.2 Particle grading curve of sand samples

根据《土工试验方法标准(GB/T 50123—2019)》[17]测定试验所选材料的基本物理参数,选用的砂土试样的级配曲线如图2所示.试样粒径在0.4～0.6 mm,可视为单一级配,这样可尽量减少颗粒粒径和级配等因素对试验过程以及对改进K-C方程的影响.

1.2 CT扫描及室内渗透试验

CT扫描技术是基于样品内部不同物质对于X射线的吸收能力不同而工作的[18],本研究选用桂林理工大学有色金属及材料加工新技术教育部重点实验室的Xradia 510 Versa高分辨率三维X射线显微镜进行砂土的CT图像采集,Xradia 510 Versa产自德国蔡司公司,包含可根据分辨率调节的多倍探测物镜,以此满足使用者的需求,其内部构造如图3(a)所示.为确保研究合理性,需要扫描到足够多具有代表性的孔隙,最终确定扫描分辨率为7 μm,获得每组1 010张1 000 px×1 024 px的CT图像.为防止CT扫描开始和结束阶段X射线扩散不均匀对试验带来影响,去除每组前后各50张图像,最终以每组910张图像进行研究.

为了更精确地确定土样的渗透系数,采用柔性壁渗透试验来确定试样的渗透系数,即利用带3个标准体积压力控制器的全自动三轴仪(见图3(b))进行试验,渗透试验示意图如图3(c)所示,其中底压控制器控制进水水头,反压控制器控制出水水头,渗流方向为由下向上进行.相对于常规的刚性壁渗透试验,柔性壁渗透试验能较好克服容器壁效应,避免水流优先沿壁渗透而非沿试样渗透的问题[19],同时还能较好地控制试样的饱和度,能精准控制试样两端的水头压力.试样的直径为50 mm、高为100 mm,设置不同水力梯度及不同围压,试样选取最大水力梯度不高于5.

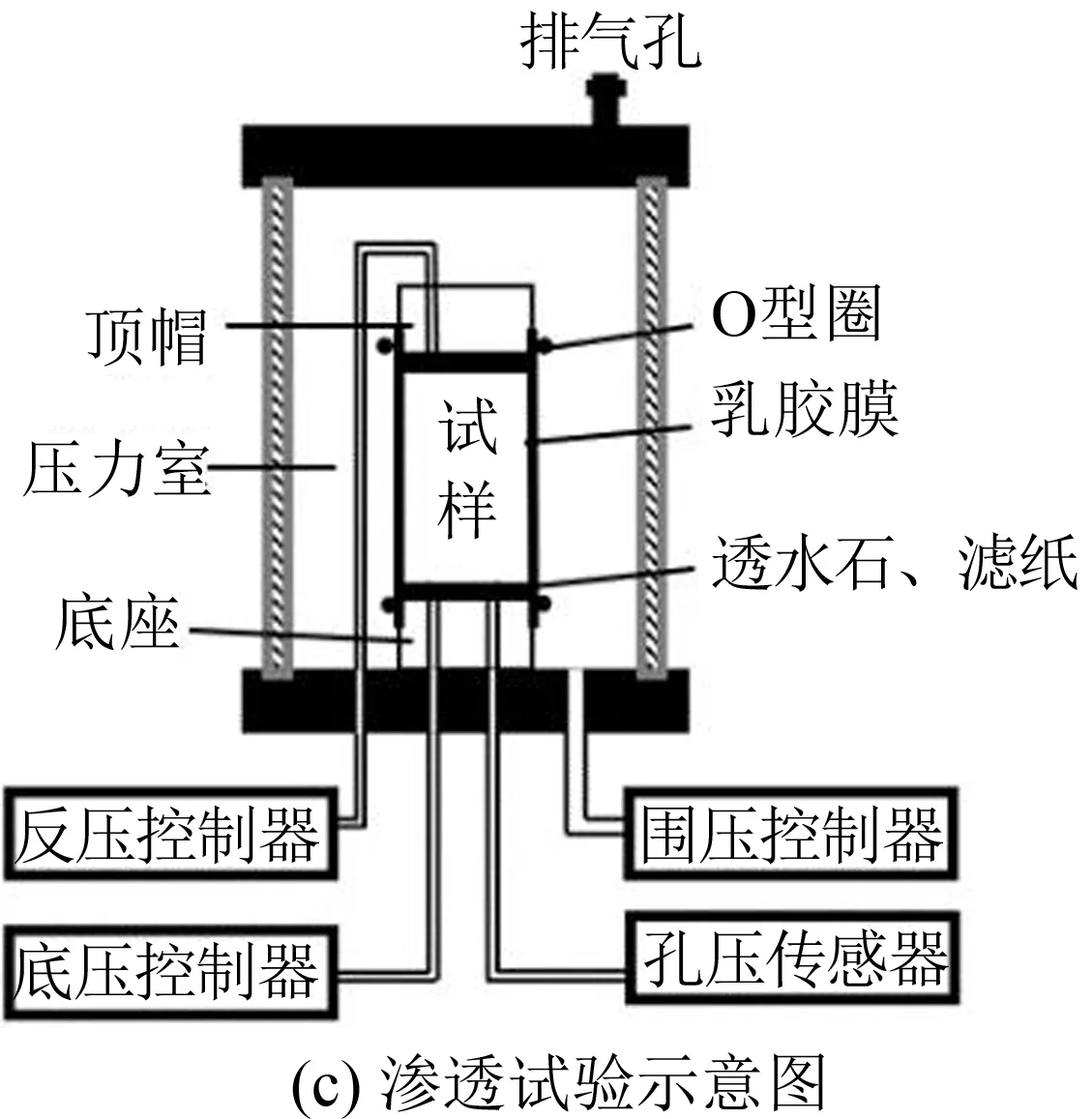
图3 实验仪器及渗透试验示意图

2 试验结果与分析

2.1 CT图像处理

获得CT图像后,需要对图像进行一定处理,去除在扫描时由于系统噪音而出现在CT图像上的无数像素点,即需对图像进行滤波处理.采用非局部均值滤波进行处理,非局部均值滤波处理的图像几乎去除了所有的噪点,并能保留完整的边界信息[20].

为了区分颗粒和孔隙,需要通过阈值分割将颗粒和孔隙分别二值化,使用最大类间方差法进行阈值分割,玻璃珠、石英砂和玻璃渣颗粒的灰度阈值分别为20 091、8 063、31 198,结果如图4所示.计算得到各切片的孔隙率分别为0.37、0.40、0.41,如图5所示,和制样时控制的孔隙率P(n=40%)基本一致.图像经二值化处理后,用Vincent[21]提出的分水岭算法来进行孔隙和颗粒的分离.以石英砂为例,图像处理过程如图6所示.

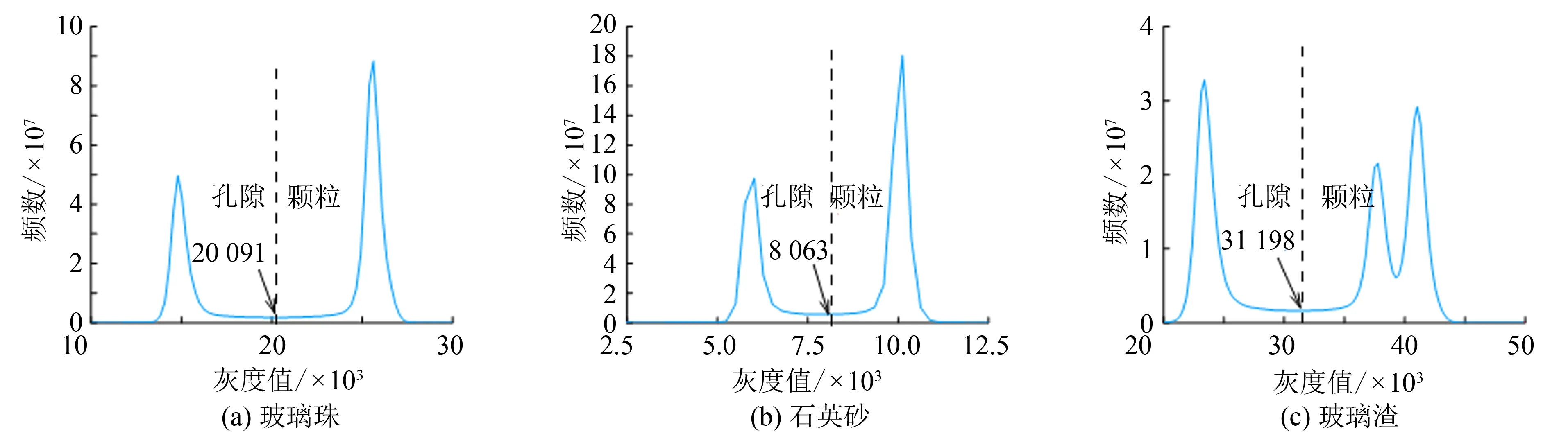
图4 CT图像处理的灰度直方图Fig.4 Gray histogram of CT image processing

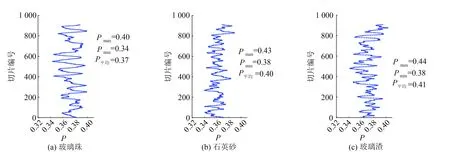
图5 二值化图像孔隙率Fig.5 Porosity of binary image

图6 石英砂图像处理过程

2.2 表征体元(REV)分析

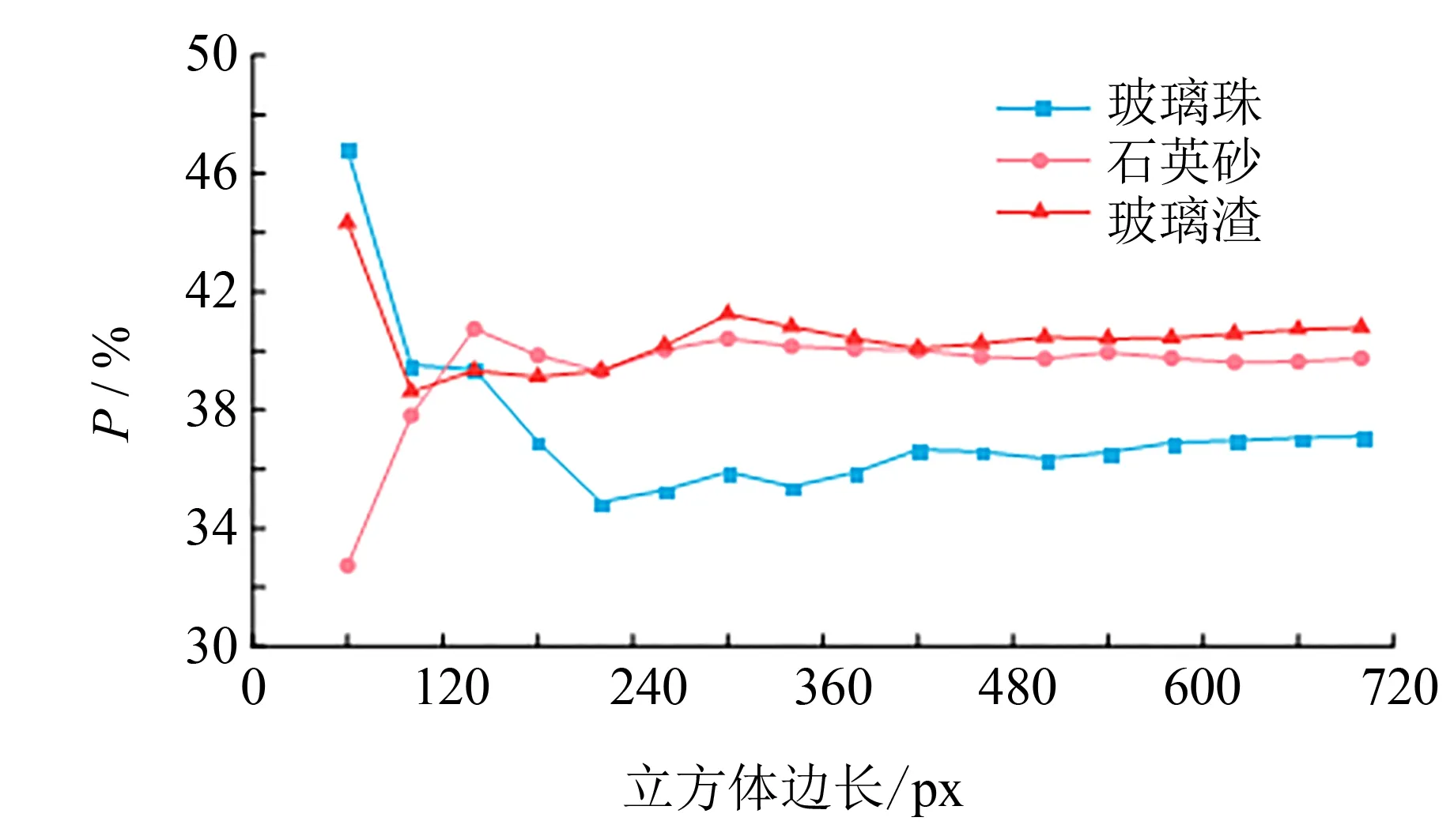
图7 体元边长和孔隙率关系Fig.7 Relationship between voxel side length and porosity

合适的代表性体积单元(REV)需要同时满足计算效率和物理特征的代表性.选取了17个立方体边长进行计算,结果如图7所示.可知当选取的立方体边长为420 px时,各体元的孔隙率与二值化处理后图像的孔隙率相近,且随着边长像素的逐渐增大,体元的孔隙率值趋于稳定,该尺寸是可以代表颗粒物性的最小尺寸,因此最终选取REV边长为420 px.图8～9为重构后的颗粒、孔隙三维图像.通过图片可以清晰看出3种不同材料的颗粒形状及孔隙的差异.玻璃珠圆润,近似球体;而玻璃渣的颗粒接近扁平状,棱角分明;石英砂介于两者之间,呈块状堆砌.

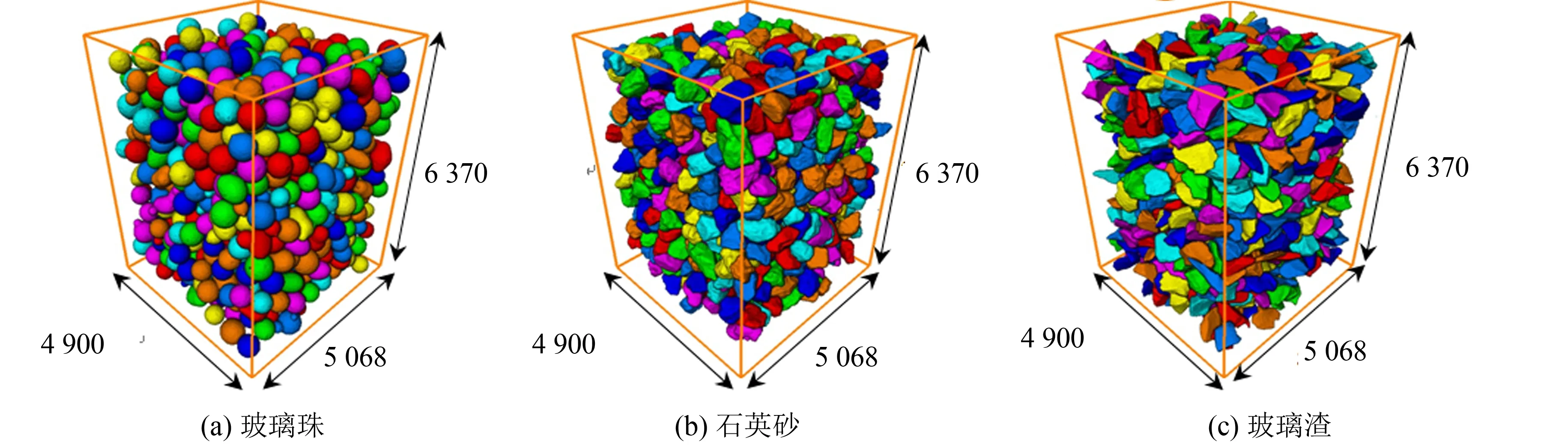
图8 砂土颗粒三维图像(单位: μm)Fig.8 Three-dimensional image of sand particles(unit: μm)

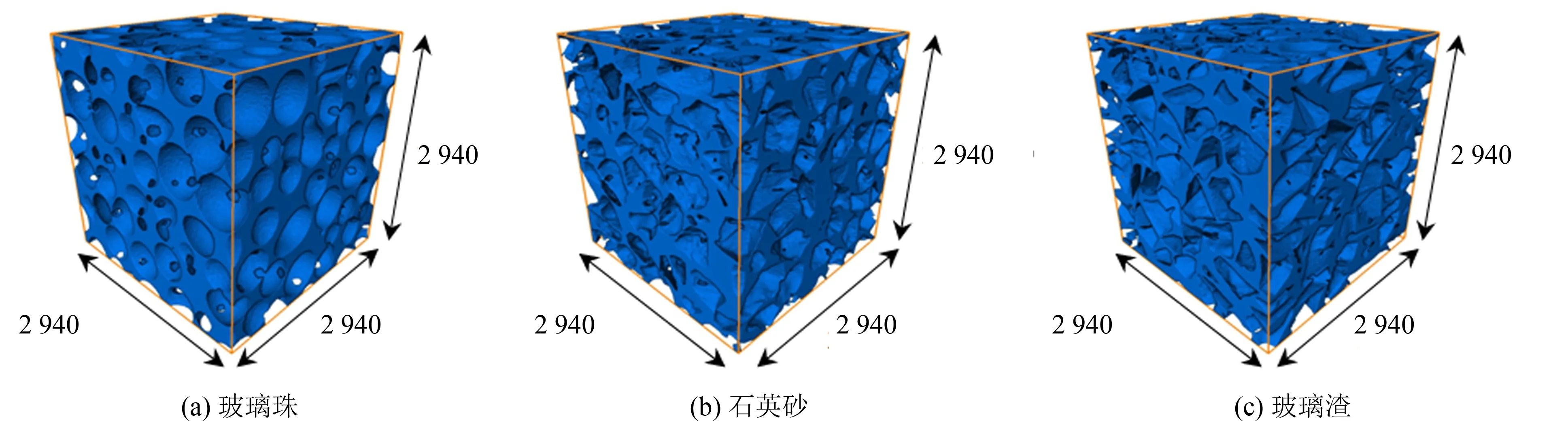
图9 砂土孔隙三维图像(单位: μm)Fig.9 Three-dimensional image of sand pore(unit: μm)

2.3 砂土颗粒形状参数分析

表征颗粒形状的参数种类较多,选取三维参数时应从颗粒平面形状、厚度与平面大小的关系、立体轮廓3个方面考虑.分别选取了伸长率(FI)、扁度(EI)和球度(S)3个主要形状参数来进行分析.将这3个参数的算术平均值作为一个新的形状参数,定义为整体形状参数OR,以此来综合考虑这3个方面对颗粒整体形状进行量化.

采用费雷特直径来对颗粒长(L)、宽(B)、厚(H)进行定义,费雷特直径为一组两个平行的与颗粒相切的切线的距离,长为最大费雷特直径,宽为与长正交的最大费雷特直径,厚为与长宽所在平面的正交方向的直径,如图10所示.伸长率(FI)定义为宽与长的比值,扁度(EI)定义为厚与宽的比值,球度(S)定义为和目标体积相同的球体的表面积与实际表面积的比值.

计算所有砂土颗粒形状参数后,取各形状参数出现频率峰值所对应的数值作为其代表值,统计在表1中.当砂土颗粒形状越复杂,各形状参数的值越小.

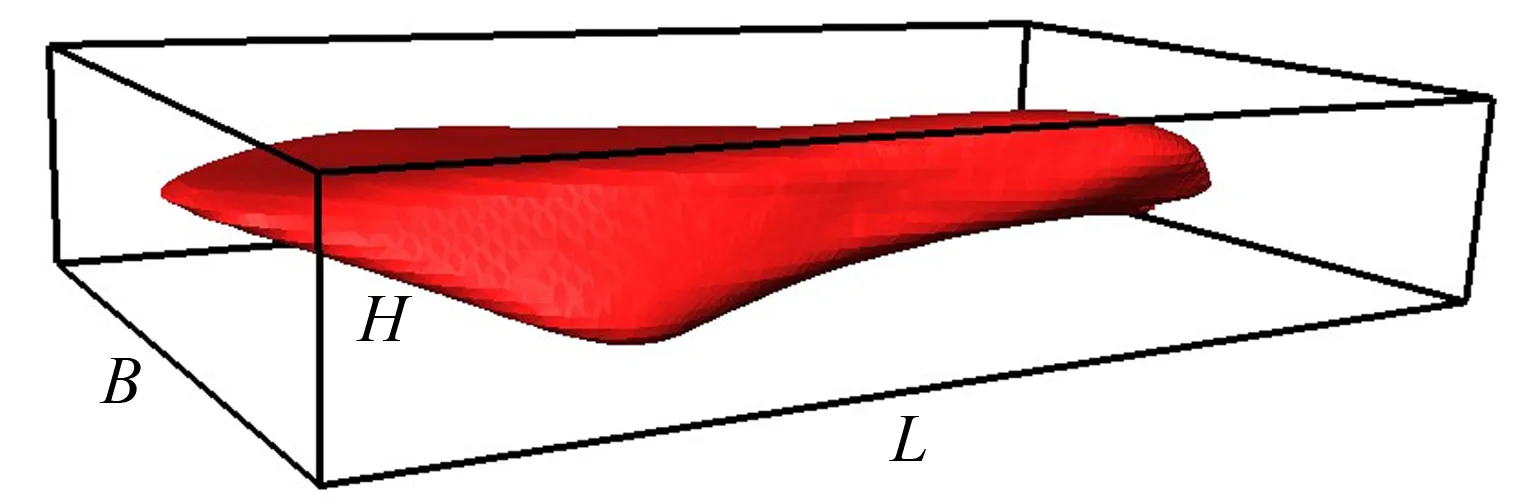
图10 长宽厚定义示意图Fig.10 Length,width and thickness definition schematic

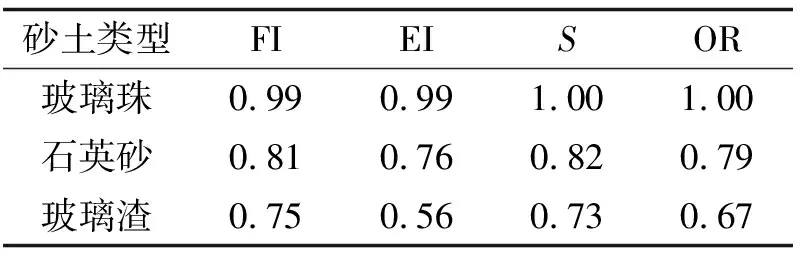
表1 砂土颗粒形状参数代表值

根据相关研究[22],当采用单一标准难以作为评价颗粒形状的参数,而采用多个形状参数组合而成的整体形状参数比单一形状参数更加合理.如表1中颗粒的伸长率(FI)与球度(S)的数值较为接近,而扁度(EI)与两者数值差距较大,整体形状参数OR的数值介于各项指标之间,且整体形状参数OR值与颗粒形状复杂程度呈高度负相关,因此其作为颗粒形状的评价标准合理.

更进一步,在K-C方程中,颗粒的比表面积是一个重要的参数,对于规则球状颗粒的比表面积可表示为

(1)

式中:r为颗粒等效半径;d为球体颗粒直径.

而砂土颗粒的形状不是完全规则的球体,为了考虑颗粒形状的影响,在式(1)中,引入与颗粒形状相关的参数a来表示比表面积与等效直径间的关系,因此可将式(1)改写为

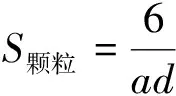
(2)

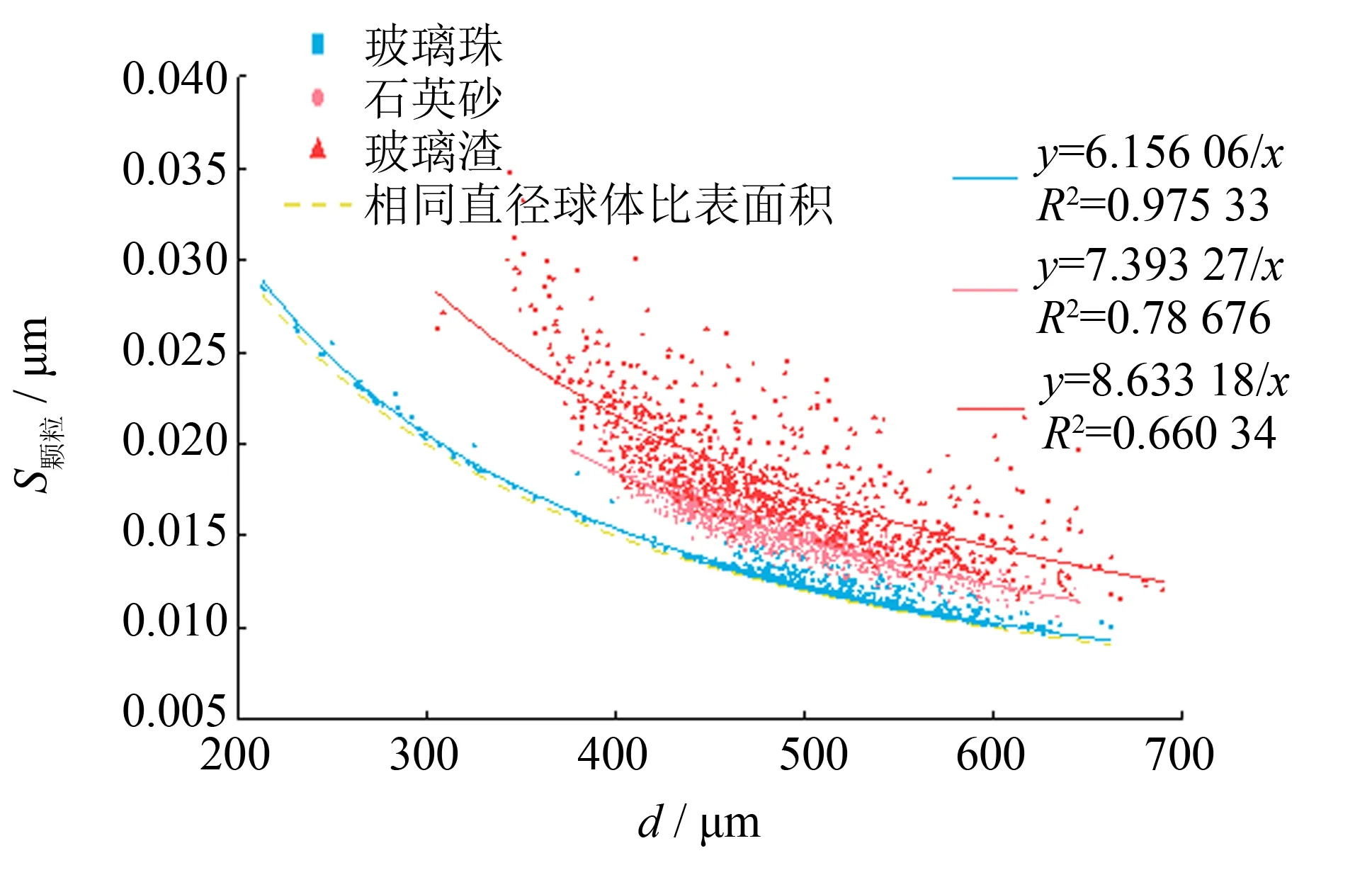
图11 颗粒比表面积分布图Fig.11 Particle specific surface area distribution

这里,a为与颗粒形状相关的参数.可知引入的结构参数a可以用来表征颗粒的比表面积,进而可方便地利用K-C方程对砂土的渗透系数进行预测.因而,利用高分辨率计算机断层扫描砂土,建立颗粒的比表面积与等效直径之间的关系.

把三维重构后砂土颗粒各等效直径计算出的对应的比表面积统计在分布图上,并对散点采用y=ax-1曲线进行拟合,如图11所示.再将各拟合函数统计在表2中,可知拟合系数a值和前文定义的整体形状参数OR之间差异率极小,具有高度一致性,因此可以将式(2)中的a值替换为整体形状参数OR替换,从而将式(2)改写成

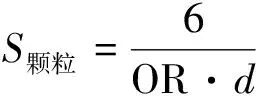
(3)

式中:S颗粒为颗粒比表面积;OR为整体形状参数;d为颗粒等效直径.

表2 各颗粒比表面积拟合方程及形状系数

孔隙比表面积也可通过引入整体形状参数OR来表示,即

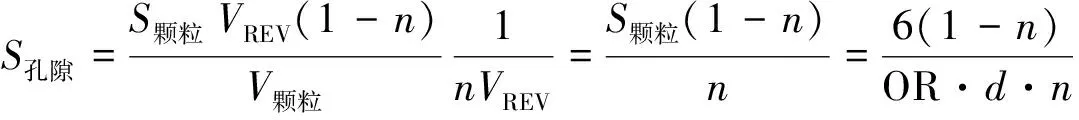
(4)

式中:S孔隙为孔隙比表面积;S颗粒为单个颗粒的表面积;V颗粒为单个颗粒的体积;VREV为体元的体积.

此外,通过提取REV的连通孔隙进行参数分析,并将孔隙参数列于表3.从表3可知曲折度T大小与颗粒形状的复杂程度呈正相关.

表3 连通孔隙结构特征参数

2.4 考虑颗粒形状参数的改进K-C模型

K-C方程最早由Kozeny提出,再由Carman改进,其适用范围广、预测效果好,受到许多研究人员的青睐.K-C方程在研究人员的改进中不断完善,因此存在多种表达形式,在此列出其经典的通用表达式,即

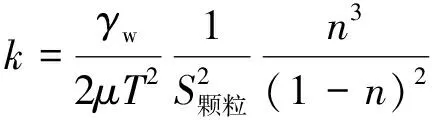
(5)

其中:γw为水的重度;μ为流体的粘滞系数,试验温度下γ/μ取值为97 728((cm·s)-1);T为曲折度;S颗粒为颗粒比表面积(m-1);n为孔隙率;k为渗透系数.

根据前文中推导的比表面积与整体形状参数的关系式,把Kozeny-Carman方程改写为三维结构参数作为变量的形式,即

(6)

或

(7)

2.5 室内渗透试验结果及改进K-C模型验证

在柔性壁渗透试验中,围压的改变会使砂土试样的孔隙结构发生改变,这一变化很直观地反映在孔隙率的改变上,为了减少围压的影响,砂土渗透系数实测值采用50 kPa围压下的试验值,将式(5)～(7)中所需参数及其计算值列于表4,对3种砂土的渗透系数的试验结果列于表5.

表4 渗透系数计算参数

表5 渗透系数预测值与试验值

由表5可知,两种改进的K-C方程计算后得到的渗透系数预测值与试验值之间差值较小,修改结果合理.对比发现,新改进K-C方程计算所得渗透系数值与试验值之间的相对误差较传统K-C方程所得预测值相对误差普遍有较大幅度的减小,改进后的含三维结构参数的K-C方程对砂土渗透系数预测的效果有所提高.

3 结语

1) 通过对玻璃珠、石英砂和玻璃渣进行高分辨率三维X射线显微镜扫描,重构了砂土三维结构,分析了颗粒形状参数,提出了一个整体形状参数OR,其值为伸长率(FI)、扁度(EI)和球度(S)等3个形状参数的算术平均值,能较好地评价砂土颗粒形状,颗粒形状越复杂,OR值越小.砂土的孔隙结构参数值会随着颗粒形状参数值的减小而增大.

2) 柔性壁渗透试验结果表明,砂土渗透系数随着整体形状参数OR的减小而减小,即颗粒形状越不规则的砂土渗透性能越差.

3) 基于颗粒比表面积的参数和孔隙比表面积定义,引入整体形状参数OR将经典的Kozeny-Caman方程改写为将三维结构特征作为变量的形式.改进的K-C方程预测砂土渗透系数值与试验值相对误差较小,且相较经典通用表达式预测效果有所提高.但还是存在一定误差,可能是由于柔性壁渗透试验中围压影响砂土曲折度进而影响渗透性,具体的影响形式需进一步研究.