基于PISA视角的中考数学试题分析及命题建议

王涛

［摘 要］教育部于2022年印发了着重强调以核心素养为导向的课程标准，但现行评价与考试并未以核心素养为导向，中考命题改革势在必行。文章基于PISA视角对南京市2019—2021年中考数学试题进行分析并提供试题改编案例，旨在为我国中考数学试题的命制提供一些科学的建议。

［关键词］PISA；中考命题；建议

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2023）02-0004-03

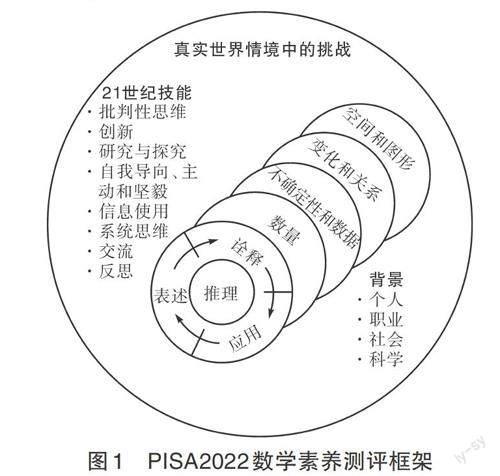
PISA是国际学生评估项目（Program for International Student Assessment）的简称，每3年进行一次。从历年PISA考查的数学内容来看，它所关注的都是数学素养，而不是单纯的数学知识和解题能力。从如图1所示的PISA2022数学素养测评框架可知，数学推理是轴心，数学情境是背景，数学内容作为载体，数学问题明确指向。

我国教育部考试中心2006年就启动了学生能力国际评价PISA2006中国试测研究项目，尝试通过评估实践，参照国际先进的教育评价理念、理论及技术，构建符合中国实际的教育评价体系。

教育部于2022年印发了着重强调以核心素养为导向的课程标准，要求教师设计的课程目标要指向核心素养，在教学中要关注真实情境的创设，促进信息技术与数学教学的深度融合，重视培养学生综合运用数学及其他学科的知识来解决真实问题的能力。但现行评价与考试并未以核心素养为导向，中考命题改革势在必行。本文基于PISA视角对南京市2019—2021年的中考数学试题进行分析，并提供试题改编案例，以期为我国中考数学试题的命制提供一些科学的建议。

一、2019—2021年南京市中考数学试题与PISA2012试题的对比

2019—2021年南京市中考数学试题共有26道或27道题，PISA2012试题有11个单元共26道题，在题目数量与分布上二者比较相似。PISA2012试题全部涉及真实情境，其中个人、职业、社会情境較多，科学情境略少。南京市中考数学试题约70%的题目都是无情境题，这意味着纯考查数学知识与技能的题目约占七成。通过语言特征来考查知识掌握情况，无关实际数学问题的解决，这是我国数学学业考试与PISA测评之间存在差异的原因之一。

南京市中考数学试题的数学特征高于PISA2012试题的数学特征，这表示南京市中考数学试题的解答步骤比PISA2012试题更复杂，究其原因是南京市中考更侧重于数学计算能力的考查，这也符合江苏省重视培养学生的计算能力与问题解答能力的现状。

二、基于PISA视角的南京市中考数学试题改编案例

通过与PISA试题的对比，我们会发现南京市数学中考数学试题中的情境题有点流于形式，仍然比较重视对纯数学知识与技能的考查。为了发展学生的核心素养，便要进行中考命题改革，要在试题编制“真实情境—问题—推理”上下功夫，做到以考促学，将课程与教学、考试评价统一起来。以下是对南京市中考数学试题中的个别题目进行改编的案例。

（一）编制案例一

原题是2021年南京市中考数学试题第24题，属于个人情境类别，考查内容是变化和关系，主要考查一次函数的应用。能根据题意结合图像理解实际问题是解题的关键。但此题的情境设置流于形式，题中提到的“乙的速度是甲的2倍”，在现实生活中，无论是步行、骑车还是开车都很难做到。对此，笔者对本题做了如下改编：

如图2，张华和张丽是龙凤胎，他俩都有新自行车，而且车把手都装有计速器。计速器可以让他们知道，他们骑行的距离、总路程的平均速度以及路程中不同路段的平均速度。

问题1：张丽骑了3 km到达市图书馆，计速器显示她的整段路的平均速度是18 km/h。以下哪个陈述是正确的？（）

A.张丽到市图书馆花了10分钟

B.张丽到市图书馆花了15分钟

C.张丽到市图书馆花了1.5小时

D.没法知道张丽到市图书馆花了多少时间

问题2：张华骑车从家到小公园走了4 km，他花了10分钟。他骑车回家时走了近路，有3 km，他只花了6分钟。张华从家到小公园再回来的平均速度是多少？

问题3：一次，两人从家出发到学校，张丽比张华早1分钟出发，张华计速器显示的平均速度是张丽的2倍，结果张丽比张华晚到校5分钟，求张丽从家到学校所用的时间。

改编后的试题将张华和张丽这两个具体人物代入其中，把原题中抽象的[A]地、[B]地更换成学生熟悉的家、学校、图书馆、小公园，拉近了学生与情境之间的距离，使情境表征更加丰满，让学生更加投入地解决实际问题。

（二）编制案例二

原题是2019年南京市中考数学试题第25题，属于社会情境类别，考查内容是空间和图形，主要考查利用一元二次方程解决实际问题的能力。题中提到“对矩形广场进行扩建改造”“扩充后的矩形广场长与宽的比为3∶2”，但实际上全国各地很少有矩形广场，学生身边没有熟知的矩形广场做参照，很难有真实感。本题为了考查一元二次方程的应用硬编了情境。对此，笔者对本题做了如下改编：

如图3，市实验中学校外有一个矩形的“开心农场”，学生可以在这里收获自己种植的农作物。因今年新生多，学校要对“开心农场”进行扩建改造。原来的“开心农场”长[50 m]，宽[40 m]。每平方米扩充区域要添加6斤营养土来改良土壤，且扩充后的“开心农场”的外围要围上栅栏。下表显示学校负责人的采购报价：

[名称 单价 营养土 0.5元/斤 栅栏 16元/米 ]

问题1：如图4，扩充后的“开心农场”长与宽的比要求为3∶2。如果计划扩建改造总费用为15000元，那么扩充后的“开心农场”的长和宽应分别是多少米？

问题2：若将原来的“开心农场”扩建改造成圆形，你能帮学校负责人在图5中画出最省钱的扩建图吗？计算此时需要的总费用（结果精确到1元）。

改编题将“矩形广场”替换为“矩形的‘开心农场”，比较合理，学生也较熟悉些。结合实际，考虑到扩充区域要添加营养土来改良土壤，以及扩充后的“开心农场”的外围要围上栅栏，又基于调查到的添加营养土的比例与相关的价格，制成负责人采购报价表。这样，一道学生熟悉的富含真实情境的试题就创编出来了，搭建起了连通数学与真实世界的桥梁。

（三）编制案例三

原题是2021年南京市中考数学压轴题第27题，属于社会情境类别，考查内容是空间和图形。此题是有关圆的综合题，主要考查弧长公式、勾股定理、圆柱和圆锥的侧面展开图、等边三角形的判定和性质等知识。题目围绕“蚂蚁怎样爬行路径最短”设置两个关于几何体表面最短路径的问题，但利用“蚂蚁爬行”来设置情境，未免有点牵强，不太接近生活实际。因此，笔者对本题做了如下改编：

如图6，卡尔卡松城堡的屋顶呈圆锥形，屋身呈圆柱形，是欧洲最大的城堡，有着超过2000年的历史，每过一段时间，工人师傅就会对屋顶进行检修。

问题1：如图7，工人师傅已经勘测出该圆锥形屋顶的母线长为9 m，[B]为母线[OC]的中点，他现在位于底面圆周上的点[A]处，且[AC]的长为3π m，他要从点[A]处爬到点[B]处刷防水涂料，请在图8所示的圆锥侧面展开图中画出工人师傅从点[A]行至点[B]的最短路径，并标出它的长（结果保留根号）。

问题2：如图9，工人师傅位于呈圆柱形屋身的底面圆周上的点[A]处，且圆柱的高为[h]，[O]是圆锥形屋顶的顶点，设圆锥的母线长为[l]。

①工人师傅从点[A]爬到屋顶的顶点[O]的最短路径的长为 _________（用含[l]，[h]的代数式表示）。

②若已勘测出[AD]的长为[a]，点[B]在母线[OC]上，且[OB=b]。圆柱的侧面展开图如图10所示，在图中画出工人师傅从点[A]爬到点[B]刷防水涂料的最短路径的示意图，并写出求最短路径的长的思路。

改编题属于职业情境类别。用卡尔卡松城堡来创设真实情境，用工人师傅检修屋顶来替代虚拟的“蚂蚁爬行”，这样设计能使得问题中已知的数据能够以正确的方式组合起来。

以上改编了南京市中考数学试题中有关个人、社会、职业情境的题目，暂未寻到适合改编的科学情境题，这也是所有中考命题中尚未涉及的领域。PISA科学情境数学题有“旋转门”问题、“地衣”问题、“航行”问题等，只要留心观察现实世界，就可以找到科学情境数学题的素材。

三、基于PISA视角的中考数学命题建议

（一）精选现实素材，重视命制基于真实情境的数学试题

基于PISA视角的中考数学命题不应仅考查学生掌握了多少数学知识，还应考查学生在真实情境中运用数学知识解决问题的能力。因此，要重视真实情境类数学试题的命制。创设情境时，不可流于形式，要重视数学与现实生活的联系，贴近学生的生活，巧妙地把所要考查的数学知识融入现实情境中。同一情境下可以多角度、多层次开展对学生解决问题能力的考查，让学生的真实水平得以充分展示。命题者平时可以关注并收集现实世界中的真实情境相关素材，依据个人、职业、社会、科学情境等进行归类，建立素材库，以供编制中考试题时参考。

（二）紧贴生活热点，引导学生从“解题”走向“解决问题”

国内中考数学试题大多考查数学基础知识、基本技能与基本思想方法。学生在解题时机械地运用数学知识进行运算与推理，自然会感到索然无味。中考数学命题应该紧贴生活热点，可借鉴PISA曾出过的“智慧型手机的使用”问题、 “冰淇淋店”问题、“唱片排行榜”问题等，编制“钉钉打卡”问题、“外卖小哥送货路径”问题、“团购果蔬”问题等。这些问题真实、有趣且富有挑战性，更容易使学生用数学的眼光去看待生活，激发学生解决问题的兴趣，引导学生从“解题”走向“解决问题”，真正做到学以致用。

（三）适当设置开放性问题，培养学生的创造性思维能力

开放性问题指的是答案不唯一的问题，数学的开放性问题有条件开放问题、结论开放问题、策略开放问题、综合型开放问题和设计型开放问题等。传统教学中，教师和家长最为关注“常考题型”的训练，导致学生的解题越来越程序化、模式化，慢慢地消磨了学生原有的独立思考与创新的能力。创造性思维是PISA2022数学素养测评中新增的项目，创造性思维的培养也被看作一条主线贯穿我国的基础教育。在中考数学试题适当设置开放性问题的背景下，教师会主动更新教育觀念，调整教学策略，协助学生改进学习方法，促进学生的思维参与，培养学生的创造性思维。开放性问题可以助推高层次思维的发展，这就需要中考命题者继续探索开放性问题的教与学，编制出高质量的开放性试题。

［   参   考   文   献   ］

［1］  杨正朝.核心素养视角下中考数学试题的研究及启示：以2021年贵阳市中考数学试卷为例［J］.贵州教育，2022（2）：18-21.

［2］  段素芬.突出真实情境 聚焦数学推理：PISA2022数学示例的视角［J］.中国数学教育，2022（9）：19-27.

［3］  夏月园，左浩德.基于PISA标准的中考数学情境题比较研究：以江苏、浙江省中考为例［J］.数学之友，2020（5）：8-11.

（责任编辑 黄桂坚）