基于三维装载场景的车辆路径优化算法研究与实践①
陈永强, 周跃进, 黄莎杉
(1.芜湖职业技术学院智能制造学院,安徽 芜湖 241006;2.南京大学工程管理学院,江苏 南京 210093)
0 引 言
典型的车辆路径问题(Vehicle Routing Problem, VRP)包含因素有:车场点、顾客点、车辆、约束条件、道路网络以及运作目标。三维装载问题(Three-dimensional Bin Packing Problem,3D-BPP)是车辆装载问题(Vehicle Filled Problem, VFP)的一个重要分支。车辆装载问题主要包含因素有:装载容器、装载货物、约束条件、装载策略以及运作目标[1]。学者在面临路径与装载联合优化时,多采用降维的方式,车辆装载以空间利用率的形式加入目标函数,降低算法难度,且模型的构建只针对单一的案例进行,与实际存在一定的差距,因而3D-BPP仍具有很大的改善空间和研究价值[2]。
1 车辆路径问题(VRP)数学模型
VRP数学模型可描述为:存在N个客户点,第i个客户点的货物需求总质量是qi(i=1,2,…,N),需求总体积是si,各个客户点需回收货物总质量是pi(i=1,2,…,N),回收货物总体积是ssi,求在满足以上提到的约束条件下的总运输成本最小。总运输成本包括与使用配送车辆数量成正比的固定成本和车辆行驶距离带来的变动成本。该文基于物流配送优化问题,在配送过程中考虑车辆最远距离、车辆装载问题、客户服务水平提升、损缺货退回等实际问题,构建较前人更为丰富、更为综合、解释性更强的数学模型。其数学模型表达如下:
1)固定成本。该成本包括:司机雇佣成本、搬运工雇佣成本、车辆折旧费用、车辆轮胎损耗、车辆日均维护费用等。为了使模型解释性更强,加入成本系数,见公式(1)。
α1·fk·M
(1)
2)总变动成本。车辆总变动成本主要与车辆行驶距离呈正相关关系。研究发现路况不同对配送车辆的速度、损耗、运行时间等会有一定影响,需要在配送基础模型上考虑不同行驶路径产生的不同变动成本,用系数βij表示路况对车辆的影响。配送点之间一般的路况系数定为1,其他路径如果路况较之更好,则βij小于1,反之βij大于1,见式(2)。
(2)
3)时间窗约束。完成i客户的配送任务(装货或者取货)的时间为hi,任务开始的时间在客户时间窗[ei,li]内,其中ei是允许任务服务最早的开始时间,li是允许任务服务最迟的开始时间。构建软时间窗惩罚成本进行时间窗约束,见式(3),其中α3,α4作为惩罚函数系数,需要根据公司对配送服务水平的重视程度进行设定,当设定成无穷大或者较大的整数的时,则函数表示硬时间窗约束。
α3·max{0,ei-ATki}+α4·max{0,ATki-li}
(3)
4)优化目标。以车辆配送过程中固定成本、变动成本、违反时间窗惩罚成本的和作为目标函数,并且用4个调节系数进行函数适应性调节。取α1,α2为整数,并且α1≫α2,其优化第一目标为最小化车辆使用数量,第二目标为最小化总行驶距离。α3α3,α4则作为时间窗重要程度的调节参数。
综上,车辆路径问题的数学模型如下:
dij·Xijk+α3·max{0,ei-ATki}+
α4·max{0,ATki-li}
(4)
需要特别指出的是,公式(4)在具体数学模型求解过程中,需要考虑决策的变量、额定载重、限定距离、时间参数等约束条件。
2 车辆三维装载(VFP)数学模型
VFP数学模型可描述为:有m种编号为i(i∈M={1,2,3,…,m})的货物需要装入一个长宽高分别为L,W,H的容器中,已知每种货物的数量为bi,每种货物的长宽高分别为li,wi,hi,从容器的左前下角开始放置,要求在装载过程中需要满足货物不重叠、货物后进先出、保护好易碎货物以及货物需要摆放稳定等约束条件,最终求得容器中最多能够放置多少种和多少个货物。
装载模型构建主要考虑了装载过程中三维空间不可重叠、垂直方向稳定性和易碎性堆放的数学表达式[3],并且根据实际装载过程进行约束设置。其数学模型表达如下:
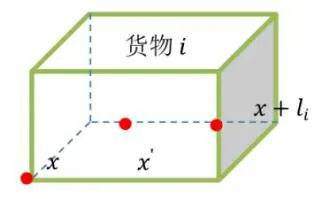
图2 不可重叠约束不等式关系
1)使用笛卡尔坐标系(x,y,z)来定位货物在运输车辆容器内的位置。坐标原点取车箱左边底部前边的顶点,如图1所示,在建立模型约束范围时尽可能准确以减少算法的搜索范围。
则得出(x,y,z)与(x′,y′,z′)取值范围:
2)三维空间不可重叠约束。设置坐标(x′,y′,z′)作为选定装载位置(x,y,z)的货品所占据的空间点,如图1所示。进一步分析,如图2以x坐标轴为例,得出x′与x的不等式关系式,并且给出了空间不重叠的约束关系式。
如图可得关系式:
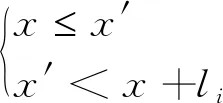
空间不重叠约束为:
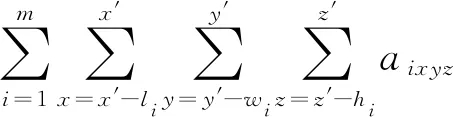
x′∈X,y′∈Y,z′∈Z
(5)
3)垂直方向稳定性约束。引入一个稳定系数αj的概念,即垂直放置在上层的货物与放置在其下层的货物之间接触面积比必须大于该稳定系数,否则判定不符合条件。因为货物默认是垂直放置,所以z轴的坐标存在关系z=z″-hi,二维俯视图如图3、图4。在实际装载过程中,基本上不会出现上大下小或者货物偏放的问题,所以会设置稳定系数αj=1,但此处为了使模型的解释性更强,考虑多种情况出现的可能。
上层货物的稳定性最低限制的表达式为:
αj·lj·wj·ajx″y″z″
(6)
两个货物接触面积存在两种情况(以横坐标为例),如图所示:
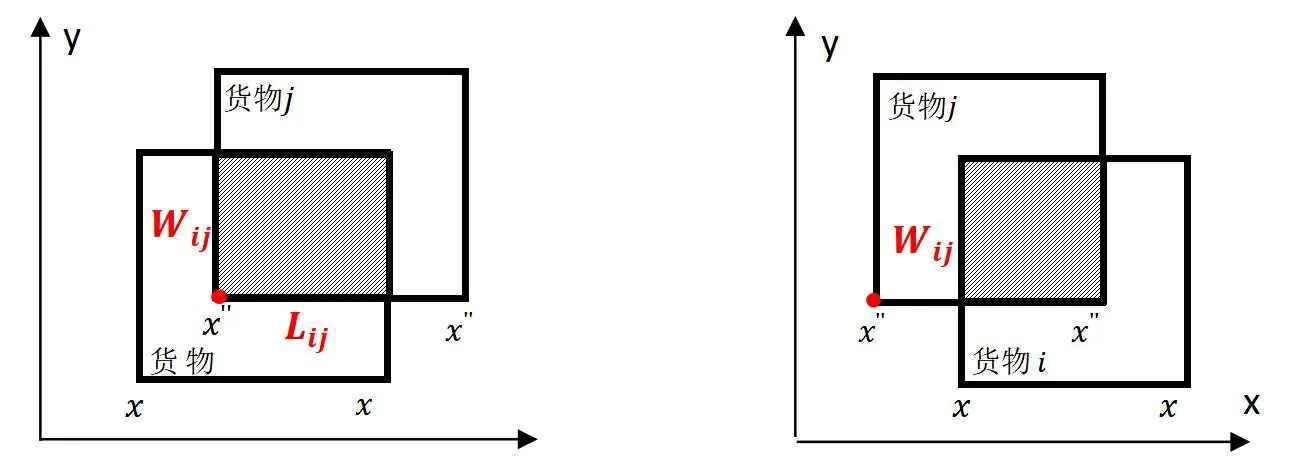
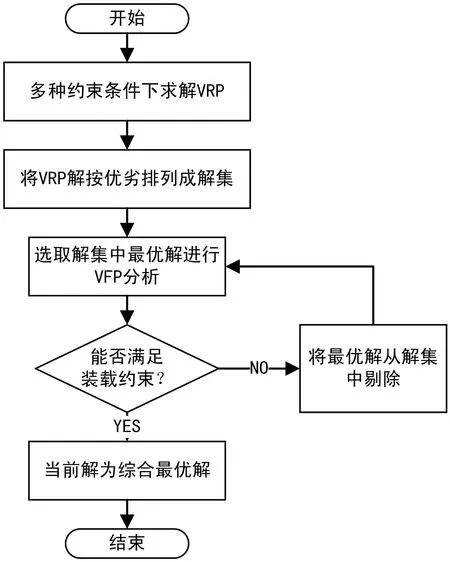
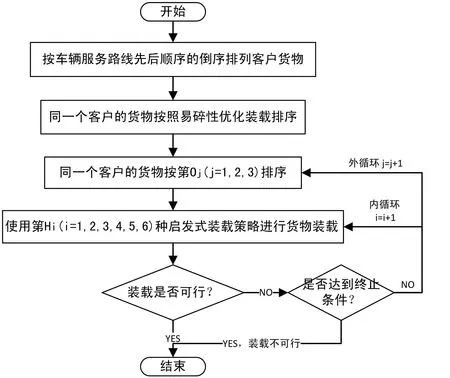
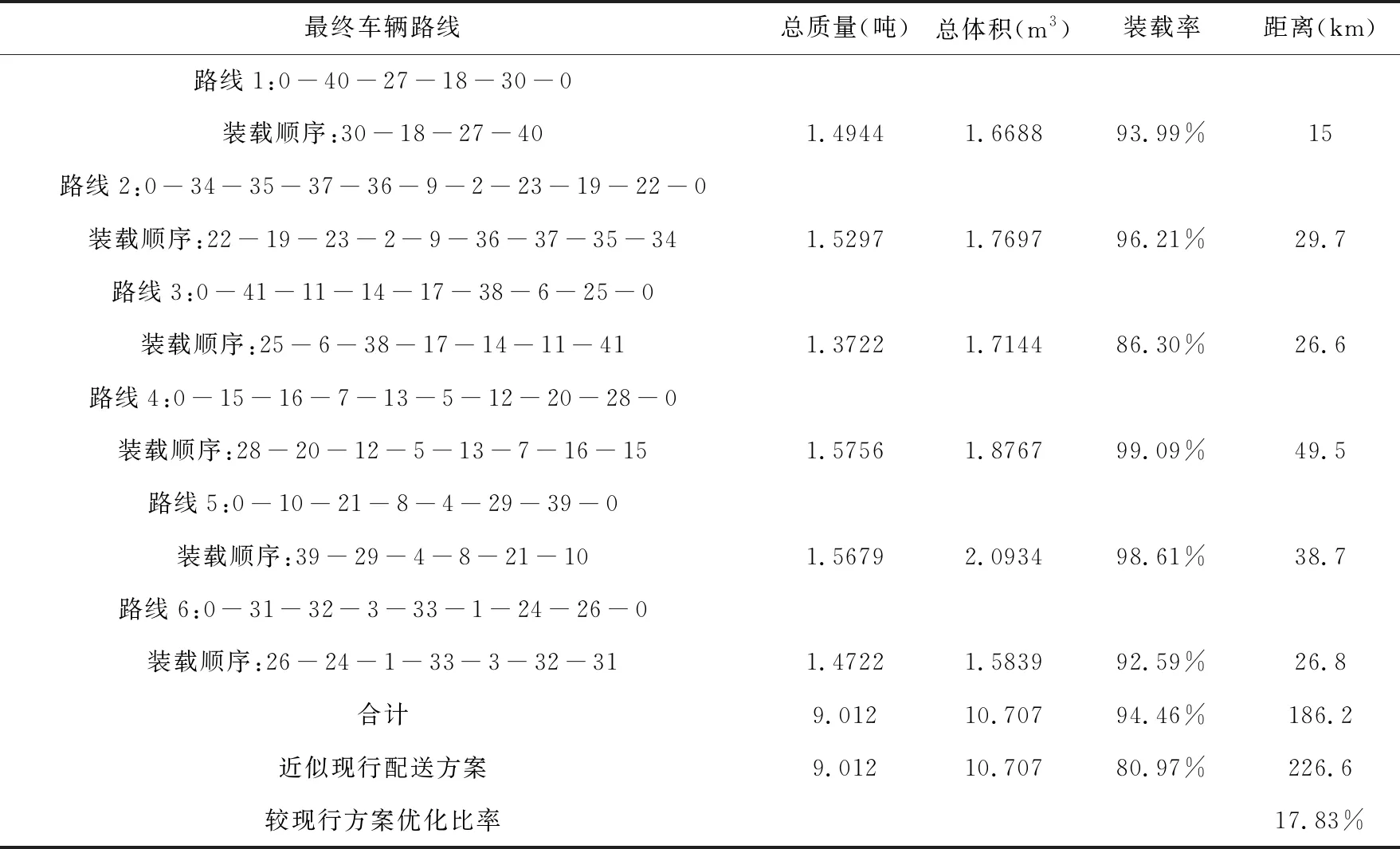
图3 x″≥x 图4 x″ 同理可得: y-wj 整理可得: Lij=min(li,lj)-|x″-x| (7) Wij=min(wi,wj)-|x″-x| (8) (9) 稳定性约束为: αj·lj·wj·ajx″y″z″ i,j∈M,x″∈Xj,y″∈Yj,z″∈Zj (10) 4)易碎性堆放约束。引入一个易碎性系数βi的概念,即表示每个货物所能够承受的最大的压强,并且通过公式“压强 = 重力(qi)/ 接触面积”表示。在讨论该约束时,需要多加入一个前提条件:稳定系数αj=1,因此才能直接使用货物的底面积作为两个货物的“接触面积”。 上层货物施加总压强表达式: (11) 货物承受压强最大限制的表达式为: βi·aixyz (12) 易碎性约束为: x″∈Xj,y″∈Yj,z″∈Zj (13) 综上,问题的数学模型如下: (14) 公式(14)在具体数学模型求解过程中还需考虑货物j最多装载数量约束;货物空间不可重叠约束、稳定性约束和易碎性约束。 VRP与VFP进行联合优化时所涉及的两个子问题的对象、类型及方向的不一样,不能简单进行整合优化,主要存在三种优化方案:以VFP为主,VRP为辅、以VRP为主,VFP为辅、VFP与VRP同时进行优化。考虑到VFP只是作为装载的可行性判定,将VFP模型作为VRP的一个约束条件,采用先进行VRP优化再进行VFP优化的策略,具体优化思路如图5。 图5 联合优化VRP &VFP流程图 依据“以VRP为主,VFP为辅”的解决思路,求解的目标是在总成本最低的情况下,保证同一路线上的货物能被装载到同一部车辆上并且能够合理地卸下。因而可以将综合模型求解拆分为两个NP问题的求解:考虑车辆多种约束的车辆路径优化与车辆三维空间装载优化。因为选择先进行VRP优化再进行VFP优化逻辑,所以不需要太复杂的装载优化算法,只需要找到一个满足装载约束条件下合理的装载方案即可。因此,三维装载部分参照六种启发式算法,根据前文构建装载模型的方式调整这六种启发式算法,用Hi(i=1,2,3,4,5,6)分别表示,并按照算法难易程度逐次进行使用和判别,直至获得一个可行的装载方案。具体装卸策略算法流程如图6。 图6 启发式装卸策略应用流程 以某公司城南配送中心为例,随机选取该配送中心某一天配送计划进行分析,并利用本文建立的优化模型和设计的算法进行验证,该中心调度员主要以区域进行订单划分,根据每个区域的当天客户需求总量安排车辆配送,该天41个客户点可以大致分为五个区域。案例计算分为两个组,每组运行计算10次,最终取10次中最优解,由于路况系数数学形式仅是体现在距离矩阵的变化上,因此主要分析比较不考虑路况系数的优化结果,见表1。 表1 不考虑路况系数最优配送路线分析 该配送中心2020年自营车辆配送成本为245.79元/吨,第三方物流配送平均成本为131.00元/吨,总平均成本为137.3元/吨。经过优化计算,车数由7辆减少到6辆,缩短了17.83%的配送距离,平均装载率由80.97%上升至94.46%,总成本1076元,平均成本119.34元/吨,与近似现行配送方案相比降低了14.5%,与2014年第三方配送成本131.00元/吨相比亦降低了8.9%。以2014年数据作为参考,某公司全省配送费用6595.21万元,以降低8%配送成本保守计算,能为该公司节约至少527.6万配送成本,提升了物流公司的综合竞争力。 基于对典型车辆路径优化策略和三维装载策略等问题的总结,建立了车辆路径问题(VRP)数学模型和车辆三维装载(VFP)数学模型,通过联合优化算法进行模型的优化求解,以实际生产案例进行可行性验证,得出以下结论: (1)车辆路径问题(VRP)数学模型和车辆三维装载(VFP)数学模型的求解需要诸多约束条件。如VFP数学模型求解时,添加了货物承受压约束、易碎性约束、空间不可重叠约束、稳定性约束等,否则方程求解结果无法有效收敛。 (2)提出了以“以VRP为主,VFP为辅”的及优化方案,并进行优化流程设计、装卸策略算法流程设计,以伪程序设计为基础,验证了“VRP&VFP”联合优化算法具备有效迭代和结果收敛的性质。 (3)以某实际配送中心数据为例进行计算和对比分析,车数由7辆减少到6辆,且缩短了17.83%的配送距离,平均装载率由80.97%上升至94.46%,运输成本与近似现行配送方案相比降低了14.5%,验证了模型和算法的正确性和有效性,具备生产实践价值。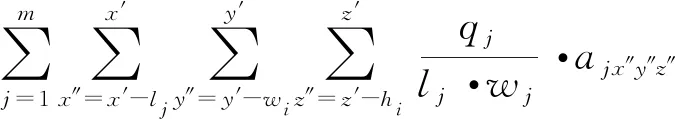
3 综合算法设计及优化
4 案例验证
5 结 论

