黏滞阻尼器在框架结构抗震加固中的应用与研究①
张 平
(安庆职业技术学院建筑工程学院,安徽 安庆 246003)
0 引 言
耗能减震技术就是在结构的选定位置增设耗能装置,在小震作用下,耗能装置和结构一并处于弹性状态,可减小结构的地震响应,使结构主体处于安全范围,一旦出现大震,这些装置可以在结构破坏前率先达到屈服状态,来消耗大部分能量。近年来利用耗能减震器对既有建筑结构进行减震加固得到了广泛关注。
1 结构模型建立及阻尼器参数设计
1.1 结构模型建立
工程结构为一栋形状规则的4层钢筋混凝土框架结构。原结构按照抗震设防烈度7度(0.15g)设计、建造,随着《中国地震动参数区划图》(GB18306-2015)[1]的正式实施,该工程建设所在区域的抗震设防烈度提高为8度(0.2g),所以需要对该工程结构进行相应的结构加固。结构高宽比是0.783,地上四层,一层层高为4.2m,二至四层层高均为3.3m,结构总重6110kN。柱截面尺寸为400mm×400mm,梁截面尺寸主要为300mm×300mm,板厚为100mm。工程软件盈建科(YJK)模型如图1所示。

图1 YJK结构模型图
此模型选用的工程实例建模通过YJK完成,但ETABS对于减震结构地震响应的分析更加全面且便捷。通过计算分析转化前后两种软件所建模型的总质量、前6阶自振周期、以及层间剪力的差值均在5%以内,这说明采用ETABS建立的有限元模型来进行结构的减震计算是可行的。
按照《建筑抗震设计规范》(GB50011-2010)[2]求选择地震波信息见表1。
1.2 黏滞阻尼器的布置及其参数设计
首先采用控制变量法进行最优位置的选择。暂定VFD参数,改变其设置位置,并提取各种设置情况下的层间位移角等地震响应。经数十组试算后数据的比对和筛选,在结构中安装28个黏滞阻尼器,根据阻尼器的布置,进行VFD参数设计,通过试算法、控制变量法对阻尼器参数进行研究,综合考虑后,选用VFD参数为阻尼系数c=1000kN·s/m,速度指数α=0.3。
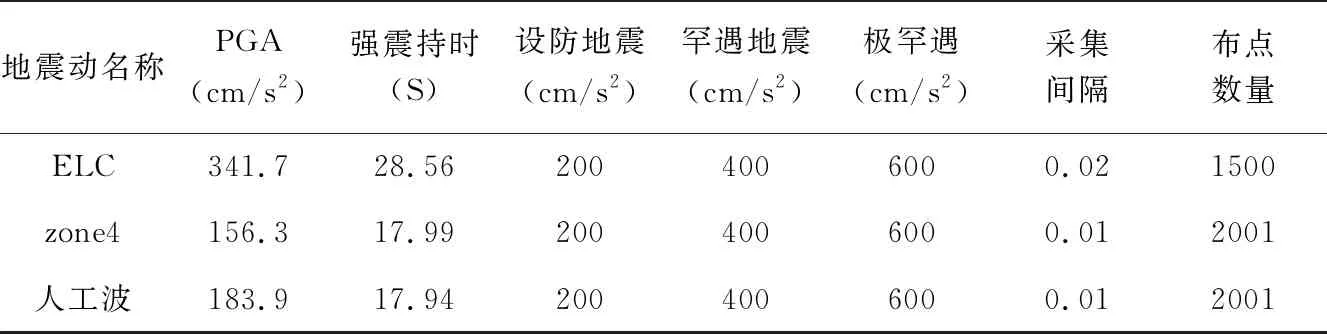
表1 地震动详细信息
2 减震结构地震响应分析
2.1 结构在多遇地震作用下的响应分析
多遇地震作用下各层位移角的包络值连线图如图2所示。
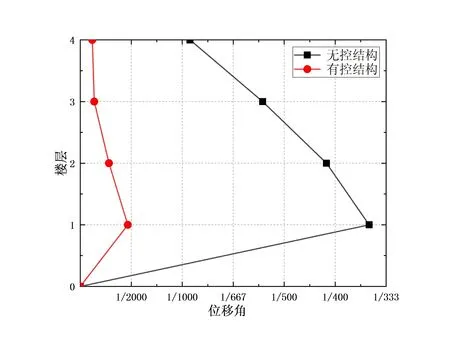
(a) X向位移角
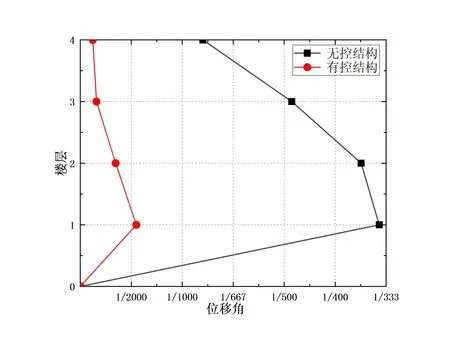
(b) Y向位移角
由图2可以看出,在无控结构X,Y方向中,第一至三层均有较大的层间位移角,不满足钢筋混凝土框架结构层间位移角小于1/550的限值要求;在设置了28个黏滞阻尼器后,各个楼层的位移角大幅度减小,各层位移角均小于规范中容许的限值。
另外,在三条地震波作用下,顶层楼板X,Y向加速度在结构设置了28个黏滞阻尼器后,减震率基本均超过50%。结构基底剪力X向平均减震率达到40%,Y向平均减震率达到36.2%。
2.2 结构在罕遇地震作用下的响应分析
基于塑性铰模型建立整体的弹塑性模型。对于梁单元采用梁弯曲铰(M3铰),对于柱单元采用柱弯曲铰(P-M2-M3铰)。计算各地震波各榀框架响应,并取典型框架代表。取三条地震波作用下层间位移角的包络值绘图如图3所示。由图3可以看出,罕遇下X,Y方向最大层间位移角出现在第一至三层,设置VFD后,各层位移角均有明显地降低。
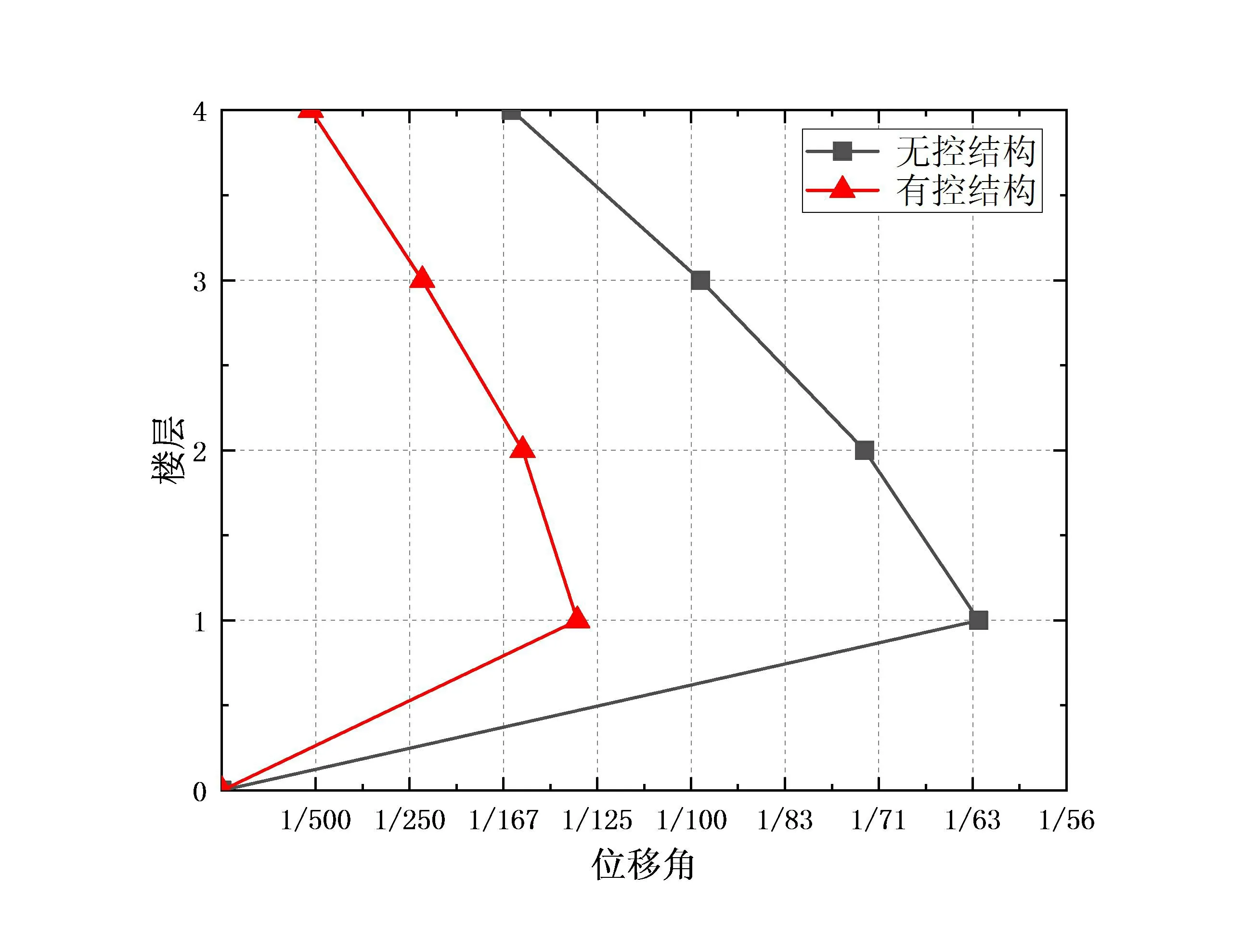
(a) X向位移角
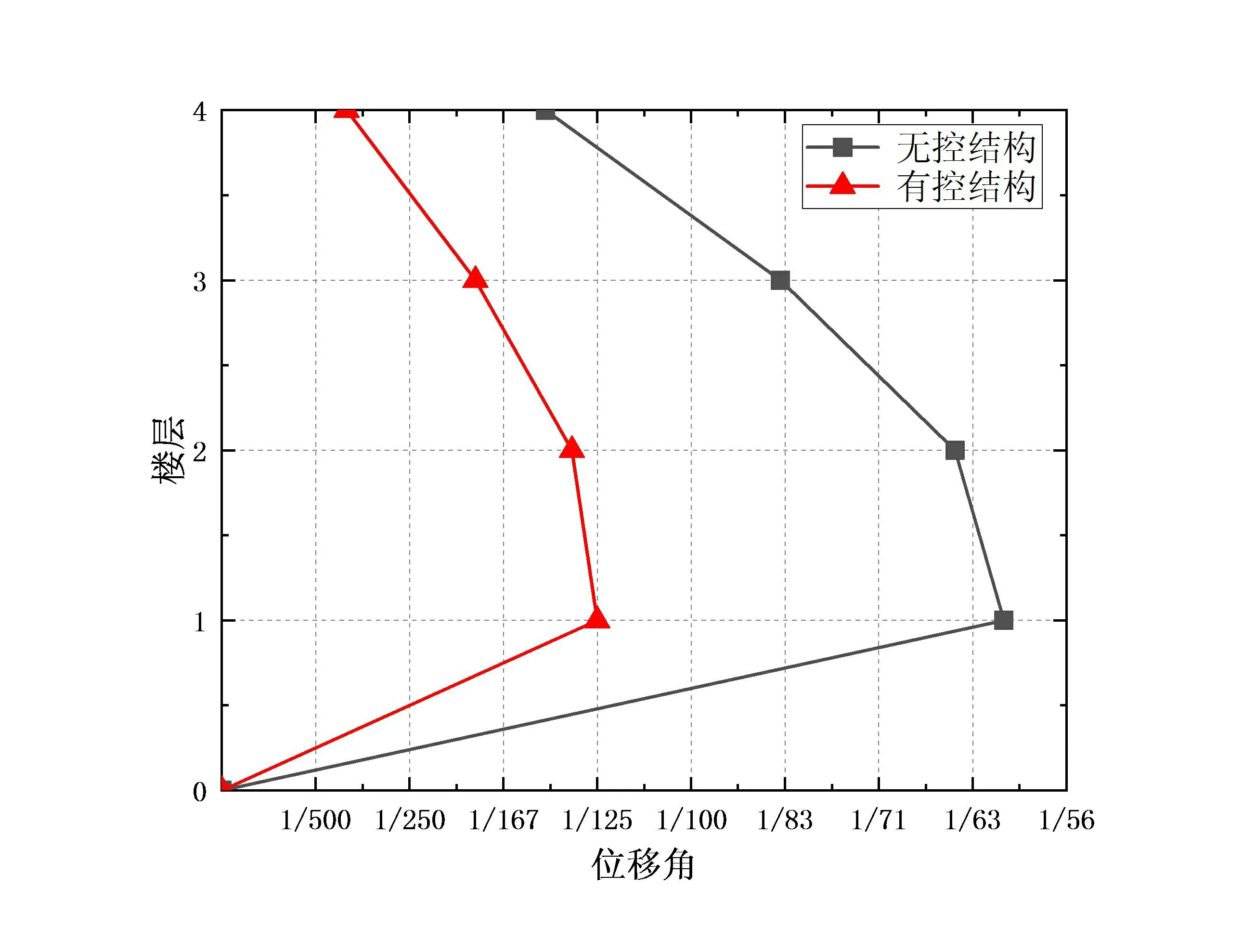
(b) Y向位移角
此外,X,Y向的顶层相对位移峰值均得到了有效的控制,减震率均达到40%以上。结构在X,Y方向上基底剪力的峰值都得到的有效的控制,其平均减震率接近40%。选取XY方向各一个阻尼器,绘制其在ELC地震波作用下的滞回耗能曲线如图4所示。
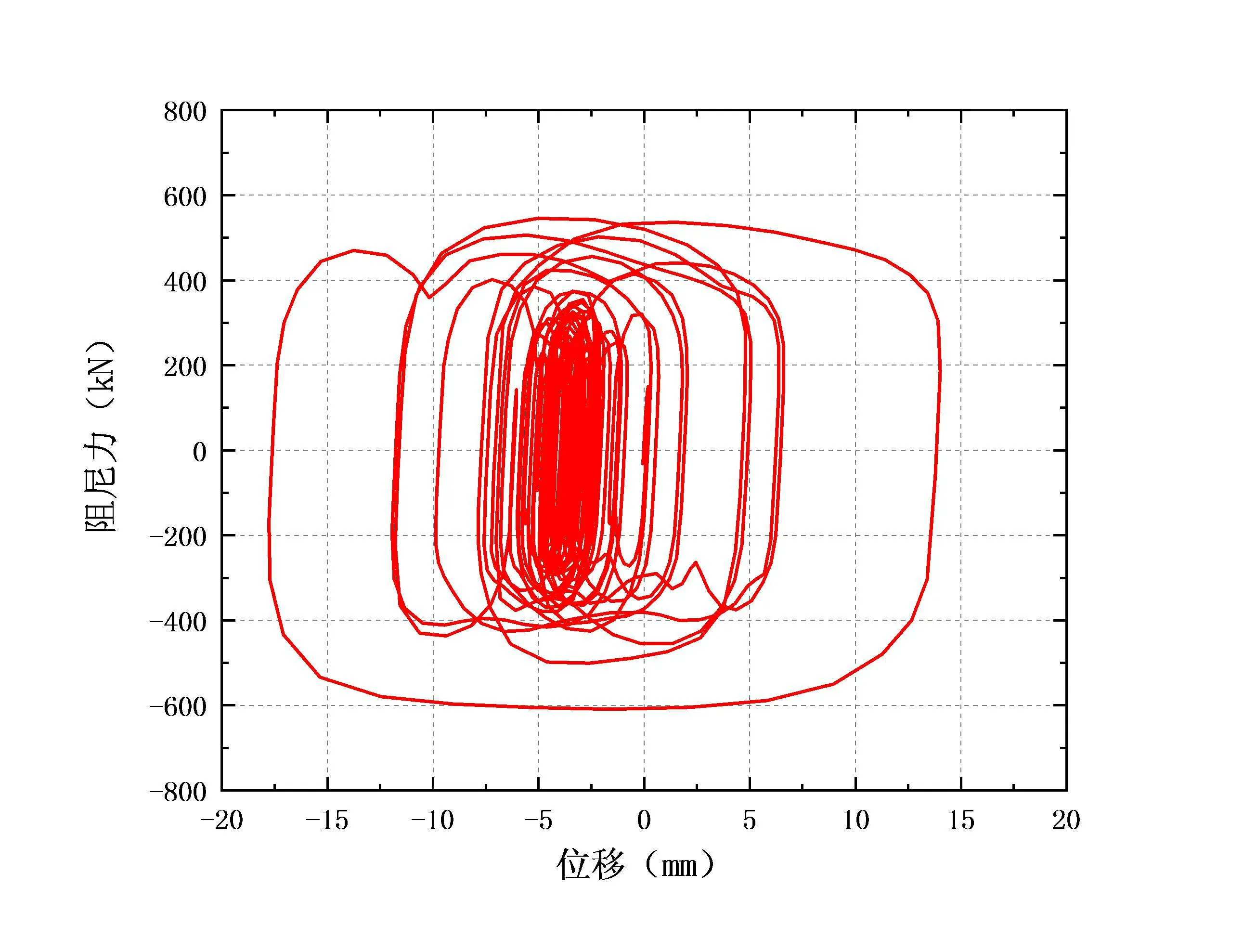
(a) X向K1阻尼器滞回曲线
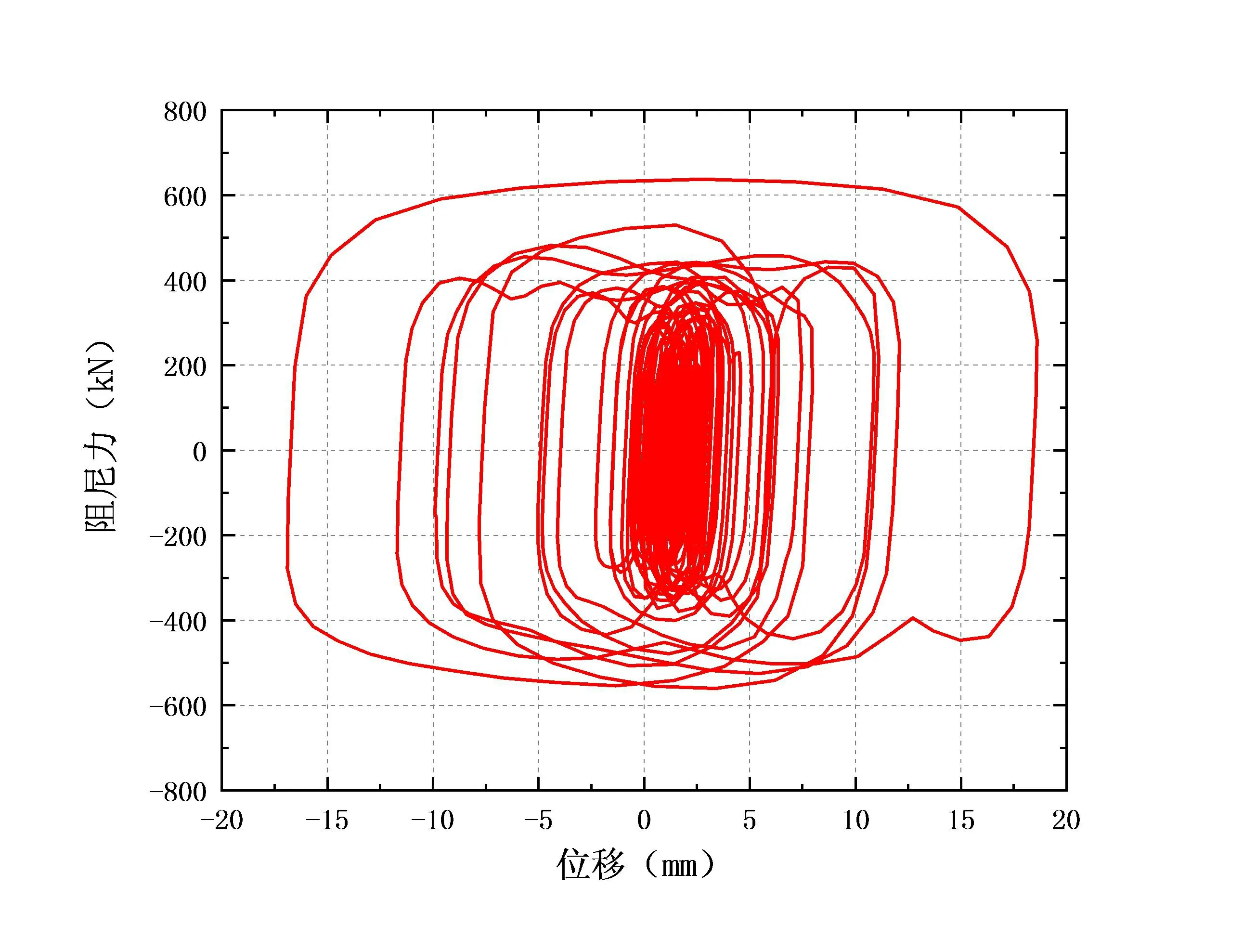
(b) Y向K17阻尼器耗能曲线
由图4可知,K1和K17阻尼器在地震作用下的滞回曲线都很饱满,整体呈椭圆形,其中K1阻尼器的最大出力达到608kN;K17最大出力达到633 kN。这表明X,Y方向的黏滞阻尼器在地震作用下均能产生很好的耗能效果。
塑性铰的屈服状态就是将它在时程分析整个过程中出现的最大转角与它自身的极限变形能力对比。根据三水准IO(立即入住,变形达到极限的10%),LS(生命安全,变形达到极限的60%),CP(防止倒塌,变形达到极限的90%),来进行塑性铰分类[3]。
未设置VFD结构,在地震波作用下,约61.9%的梁出现塑性变形,但变形较小处于“B-IO”阶段,有38.1%的梁铰处于变形较严重的“IO-LS”阶段;约73.3%的柱处于“A-B”阶段,有26.7%的柱铰处于变形较小的“B-IO”阶段。设置VFD结构,地震作用下基本无框架柱塑性铰的出现,且梁端均无处于“IO-IS”阶段的塑性铰出现,顶层梁基本处于弹性阶段。可以看出布置黏滞阻尼器后,结构整体控制变形的能力得到了显著增强。
3 基于云图法的结构概率地震需求分析
云图法[4],即选择一系列地震动对确定的结构进行抗震计算,得到相应的响应结果,根据反应结果再利用统计回归技术求得结构概率地震需求模型[5~6],这是进行地震需求易损性分析的基础。
3.1 概率地震需求模型建立
结构设防烈度为8度(0.2g),设计地震分组为第二组,场地类别为Ⅱ类,结构基本周期为0.82s。首先选择震级与震中距作为平面划分的依据,并将震级=5.7级作为分划震级强弱的边界,以震中距=30km作为分划地震距离大小的边界。从太平洋地震工程研究中心的数据库中选择108条地震波。选用谱加速度Sa(5%,T1)作为地震动强度参数(Intensity Measure,IM),最大层间位移角作为结构地震需求参数(Engineering Demand Parameter,EDP),从而得出“Sa-θmax”云图。
根据得出的云图,对Sa与θmax进行对数线性回归,分别得到无控结构、有控结构的概率地震需求模型。
无控结构:
lnEDP=0.9912lnIM-3.9572
(1)
有控结构:
lnEDP=0.8557lnIM-5.4524
(2)
3.2 地震需求易损性分析
以有、无控状态下结构的概率地震需求模型作为基础,进行结构的概率地震需求分析。
采用对数正态累积分布来表示地震易损性模型:
(3)
联立以上,则得地震易损性模型:
(4)
式(3)-(4)中,d表示结构地震需求的某一限值,Φ是标准正态随机变量概率分布函数,β是结构的地震需求对数标准差:
(5)
N为地震动记录数等于108。
根据我国抗震设计规范规定,对本结构而言,弹性阶段取θmax=1/550,塑性阶段取θmax=1/50。由此确定“轻微破坏、中度破坏、严重破坏、倒塌”的位移角限值分别为1/550,2/550/,4/550,1/50。
利用Matlab软件处理数据,可得结构在不同地震需求限值下的地震需求易损性曲线如图5所示。
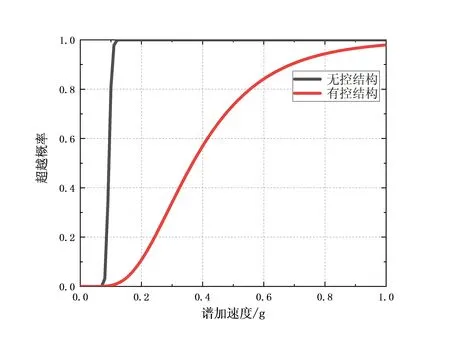
(a)d1=1/550
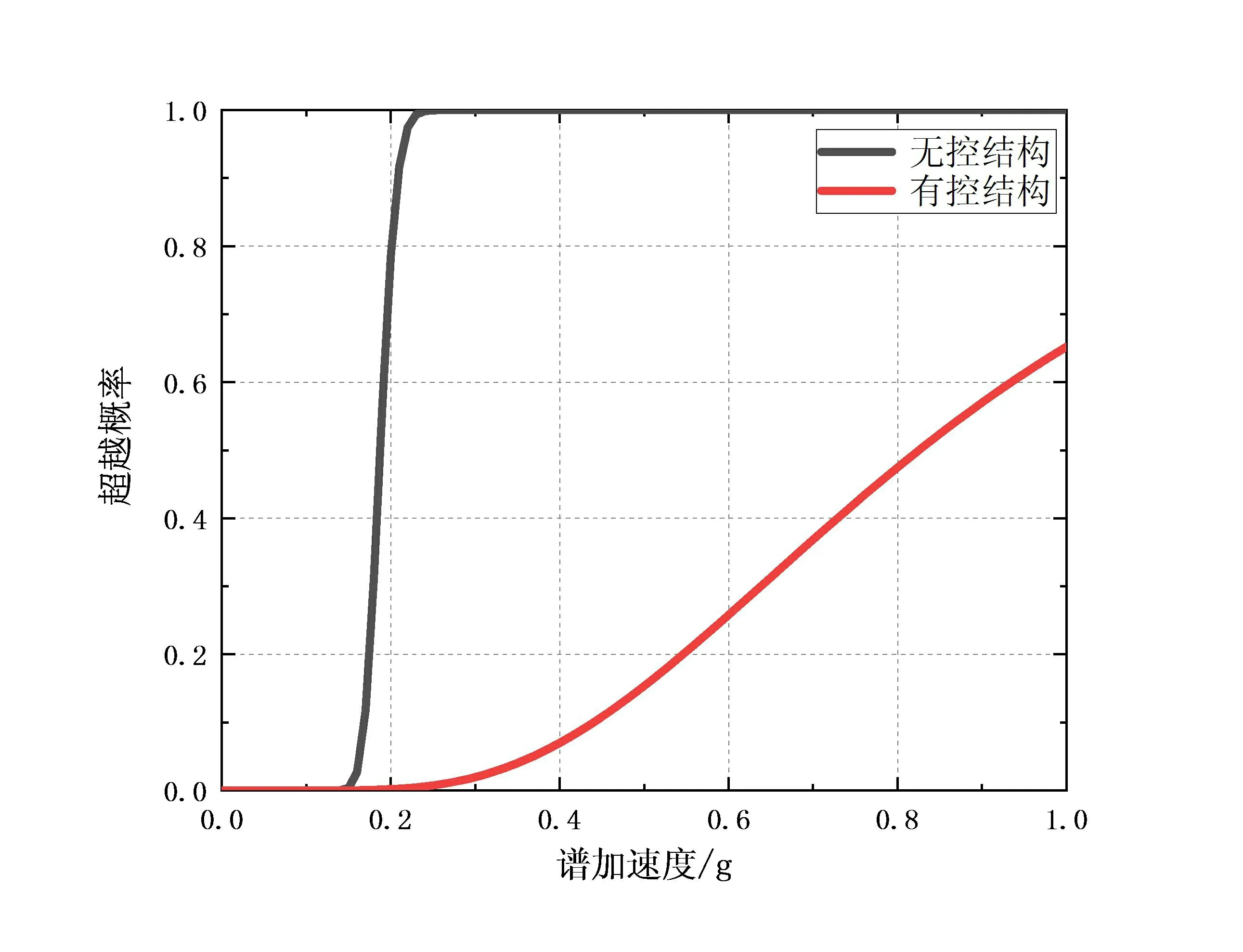
(b)d2=2/550
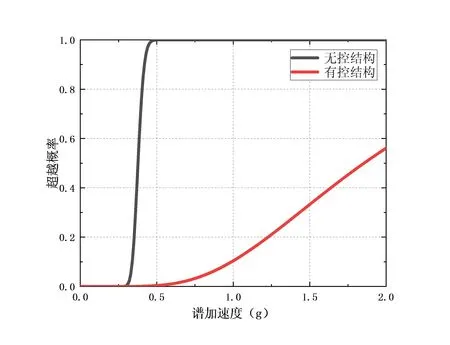
(c)d3=4/550
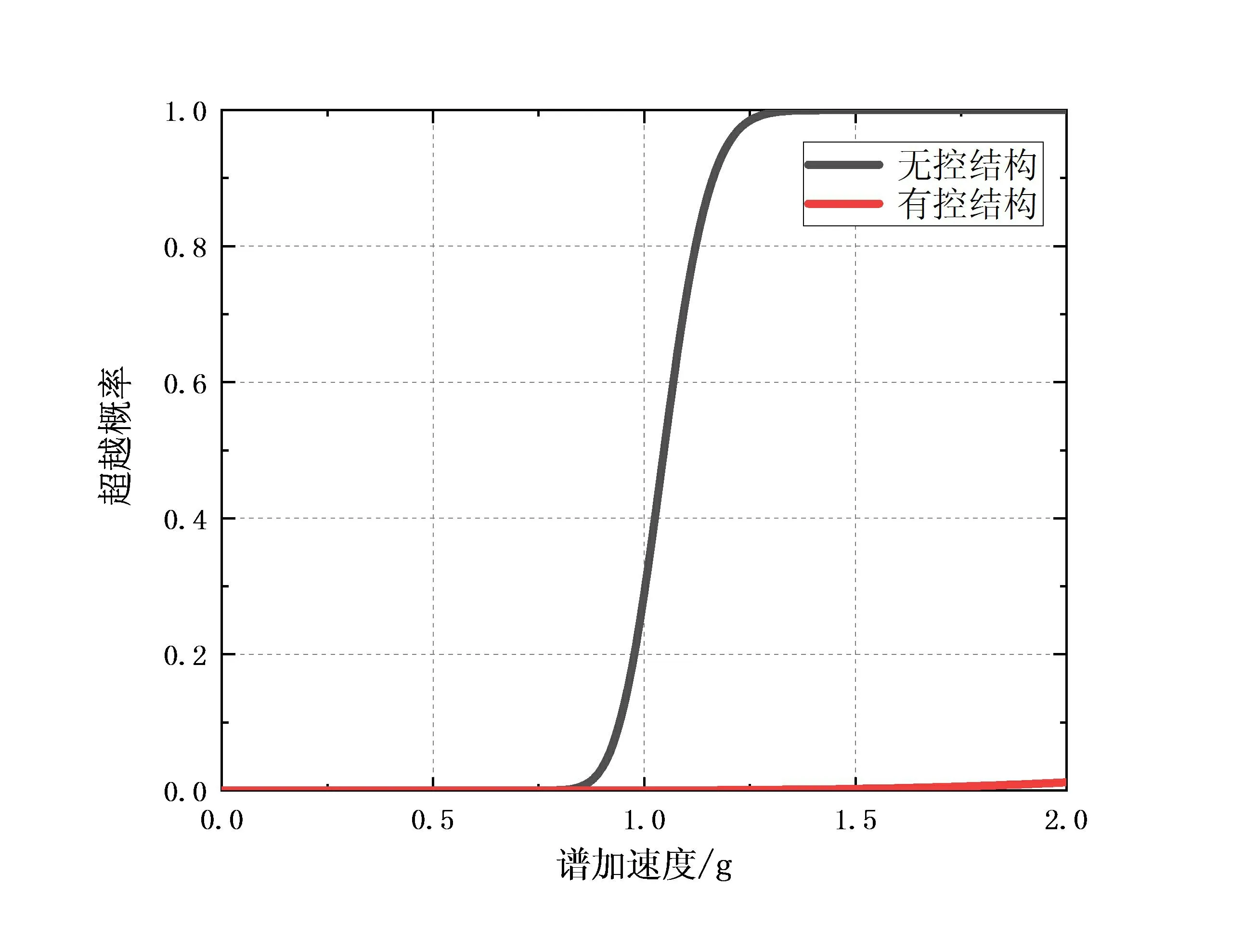
(d)d4=1/50
如图5所示,无论无控结构或有控结构,随着性能指标要求的降低(从“轻微破坏”到“倒塌”),结构的易损性曲线趋于扁平、平缓,这符合结构的设计准则和易损性曲线的性质。而当确定性能指标及确定位移角限值时,比较有无控制下的地震需求易损性曲线,可以看出有控制下的结构的曲线总是更加趋于扁平的,及在相同的Sa(5%,T1)下,有控制下的结构其对应的超越概率总是小于无控结构的。特别是当性能指标为“严重破坏”和“倒塌”时(及对应位移角d3=4/550,d4=1/50时),当Sa(5%,T1)在0g~2g的范围内时,这一差别更为明显。这也从易损性的角度说明了对于结构设置黏滞阻尼器后大大提高了结构的减震加固效果。

