古建木结构节点的抗震机理研究及抗震能力评估①
詹闽研
(闽西职业技术学院城乡建筑学院,福建 龙岩 364000)
0 引 言
榫卯节点力学性能决定着古建筑木结构的抗震性能,是古建筑研究的热点和难点[1-2]。国内外诸多学者对古建木结构榫卯节点进行了研究。Meng X等人对宋代建筑木结构的抗震机理进行实验,认为重力势能是传统木结构测试需要重点考虑的因素[3]。张锡成等人构建了离散模型,从而对殿堂式古建筑木结构的抗震性能进行分析,实验显示,该模型的误差小于7%[4]。郭宇等人对传统木结构节点的抗震性能进行分析,并根据分析结果提出了加固和修复的策略[5]。不难看出,在现有的研究中很少考虑到节点尺寸以及材料特性对建筑抗震性能的影响。针对上述问题,研究以古建筑结构中最常见的燕尾榫为例,在数值模拟的基础上,构建M-θ力学模型,从而对其抗震机理和抗震能力进行分析,为古建木的抗震能力评估和修缮加固提供数据和理论支撑。
1 燕尾榫节点弯矩-转角力学模型的构建
1.1 燕尾榫的结构特点及受力分析
燕尾榫是较为常见常见的古建木结构榫卯节点形式,其特点是榫头的根部窄、根部宽、上部大、下部小;卯口则是内大外小,节点安装一般采用自上而下的方式,常应用于柱与额枋交接部分[6-7]。一般而言,燕尾榫节点具有一定的转动刚度,以便于传递弯矩,其性质介于全刚接和铰接之间,为半刚性连接节点。一般榫卯节点在受力时处于复合受力状态作用,如图1所示。
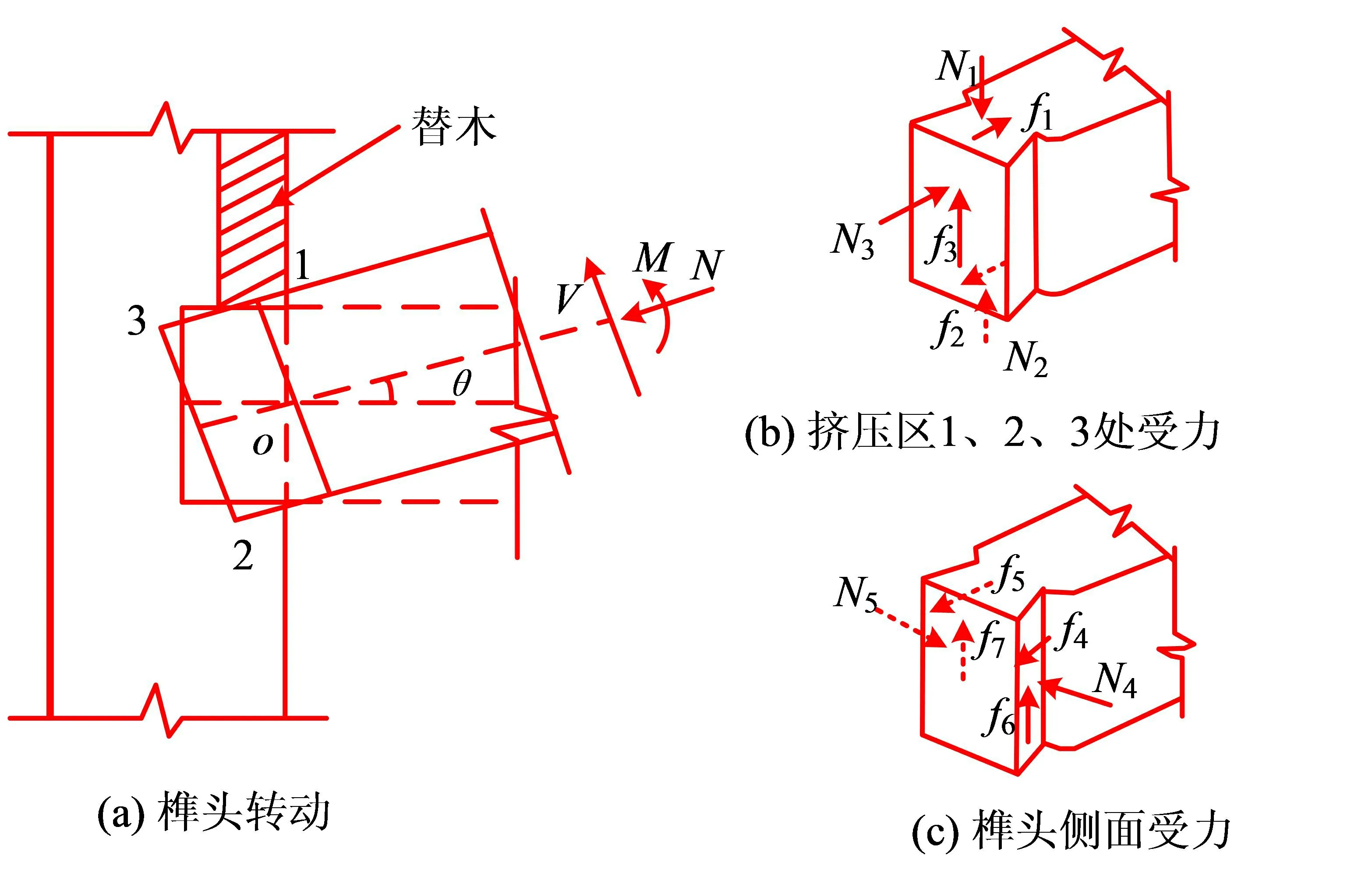
图1 燕尾榫的受力分析
图1为燕尾榫的受力机理。在图1(a)中,当燕尾榫受到外力作用的影响时,榫头以o点为圆心发生转动,转动的角度为θ,在此时,榫头与卯口相互嵌压,使得榫头的横纹受到压力,并形成3个挤压区,分别为挤压区1,2,3。在图1(b)中,N1,N2,N3分别表示在顶面、地面和端部产生的正压力;f1,f2,f3则是在正压力下在平面处产生的摩擦力。在图1(c)中,N4,N5分别表示榫头侧面与卯口内侧产生的正压力。在N4和N5的作用下,卯口向外侧扩张,从而导致两个侧面处产生摩擦力f4~f7。通过上述内容可以得知,燕尾榫榫头和卯口主要受力方式为横纹受压与顺纹受压。通常而言,在木材中,横纹弹性模量与顺纹弹性模量相比,会存在较大的差距,因此在受到较大的外力影响时,燕尾榫的榫头处会因为积压而发生变形,但卯口的尺寸变化量可以忽略不计。当θ的值不断增加时,燕尾榫的榫头形变也更加剧烈,且不可逆。根据上述内容可以得知,在地震当中,燕尾榫节点可以在不断转动和摩擦的过程中消耗地震能量,从而达到抗震的效果。
1.2 燕尾榫节点数值模型构建
以文献[10]中燕尾榫试验模型为分析对象,采用软件ABAQUS 6.14建立其数值模型,模型的尺寸、材料的规格见文献[10]。在模型建立时假设木材拉伸弹性模量和压迫弹性模量是相同的。木材弹性阶段参数选取Engineering Constants来进行定义。木材塑性阶段采用软件中的Potential 函数来定义该阶段木材各个方向的屈服应力。基于Hill 屈服准则来进行设置木材在各个方向的屈服应力比。在利用燕尾榫节点数值模型进行数值模拟时,需要保证两个条件,第一,与实验边界条件一致,第二,柱两段设置为固接。为避免应力集中设置垫块并采用绑定(Tie)于柱的右端和枋端,在两个垫块的中心分别设置两个参考点RP-1和RP-2,采用位移加载方式施加轴向荷载与低周往复荷载。参考以往文献中既有实验成果,摩擦系数取为0.4。根据上述内容,建立燕尾榫数值模型YWS1。
1.3 燕尾榫弯矩-转矩力学模型构建
在弹性段,基于燕尾榫数值模型YWS1,建立YWS2和YWS3,其具体参数见表1所示。
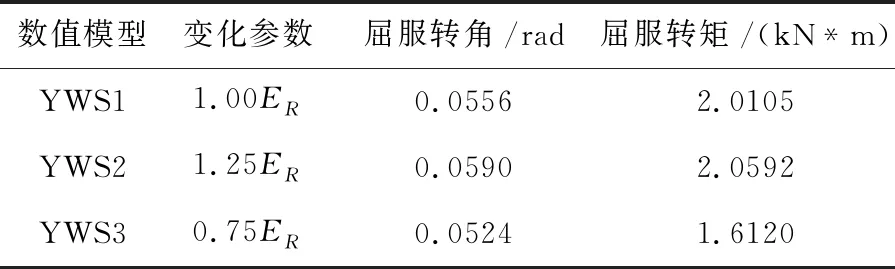
表1 3种燕尾榫数值模型的参数
表1中,ER表示YWS1的横纹径向弹性模量。当存在木材的抗压强度fc小于木材的等效抗压强度fce时,表示木纤维没有屈服,此时中性轴没有下移。此时的弹性段受弯承载力表示为公式(1)。
(1)
公式(1)中,Me为弹性段受弯承载力,M1为弹性段屈服转矩,b为榫头宽度,D为木柱直径。通过模型YWS1,YWS2和YWS3的弹性段屈服转角θ1和屈服转矩进行拟合,获取燕尾榫节点的弹性段计算方式(2)。
(2)
公式(2)中,b1为榫额宽,b2为榫颈宽 ,γ1是一个比值,其计算方式是燕尾榫榫头的顶面面积除以1/2的木柱圆截面面积。在屈服段,各个燕尾榫节点模型的极限转角θ2和极限转矩M2如表2所示。
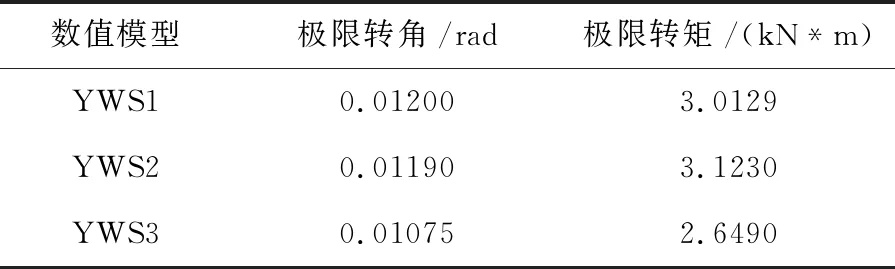
表2 3种燕尾榫数值模型的参数
在屈服段,木梁中性轴下移,木材受压侧开始出现塑性变形,木纤维被拉断并达到极限压应变。此时,木梁的最大弯矩计算公式如公式(3)所示。
(3)
公式(3)中,Mu表示屈服段木梁的最大弯矩,m表示木材抗压强度与抗拉强度的比值 。对屈服段极限转矩和弹性段屈服转矩的差、屈服段极限转角与弹性段屈服转角的差进行数据拟合,可以得到公式(4)。
(4)
在公式(4)中,γ2是燕尾榫节点的顶面面积除以木柱圆截面面积的值。综合上述内容,可以得到燕尾榫节点的M-θ力学模型,如公式(5)所示。
(5)
公式(5)中,k1,k2分别表示弹性阶段和屈服阶段的斜率。此时燕尾榫节点双折线力学模型如图2所示。
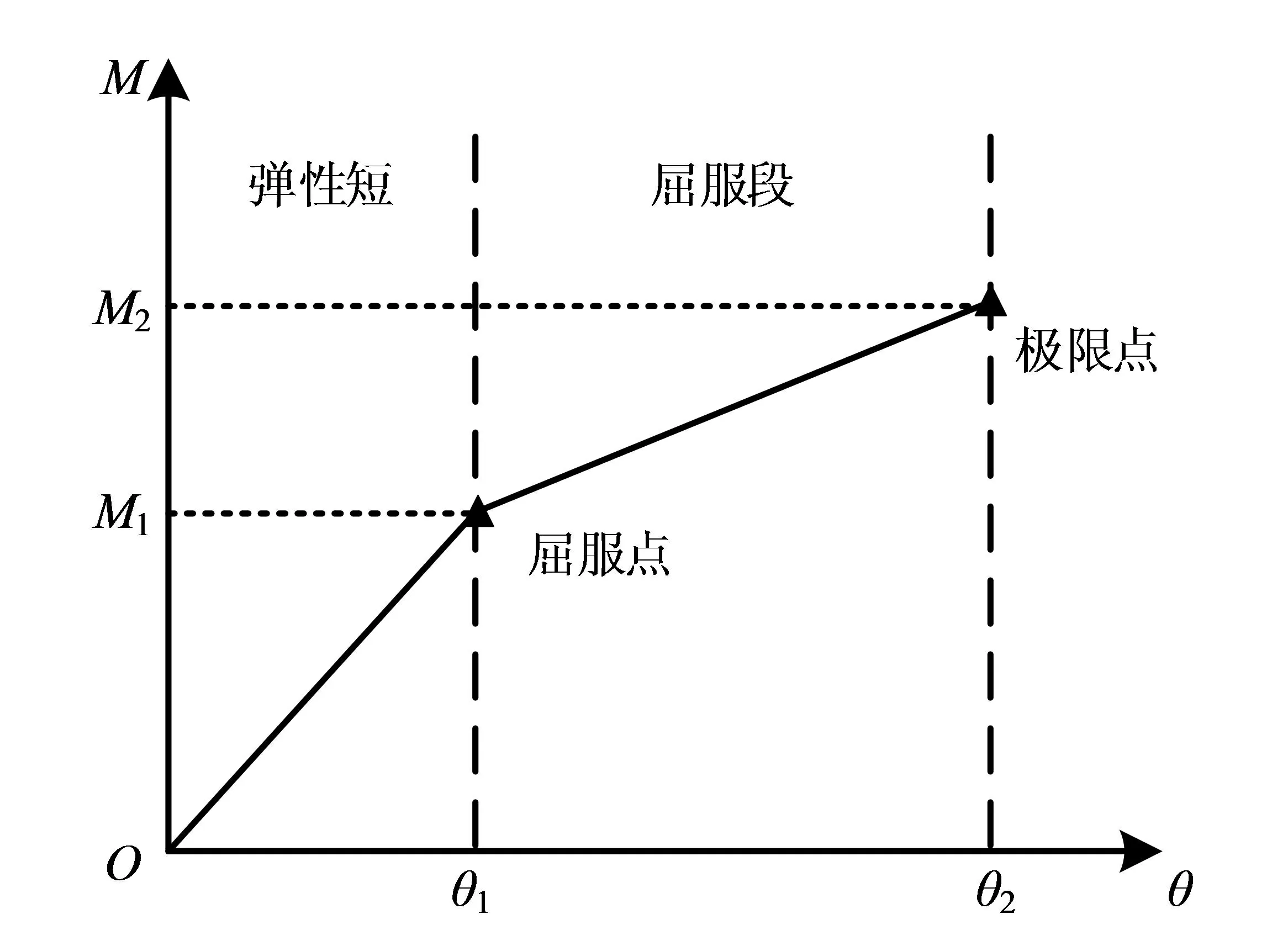
图2 燕尾榫节点双折线力学模型
在建立燕尾榫节点理论力学模型后,即可将实际节点数据代入到模型中进行计算,进而实现对古建木结构节点的抗震性能评估。
2 燕尾榫力学模型的验证
采用ABAQUS 6.14建立数值模型并与实验数据进行验证,实验M-θ骨架曲线(TEST)与数值模拟M-θ骨架曲线对比如图3所示。
从图3可以看到,数值模拟结果与实验结果吻合较为良好。实验受弯承载力和数值模拟值误差约为0.3%;负向受弯承载误差约为4.2%,这验证了所建立的燕尾榫数值模型的正确性。利用文献[10]中的4次实验数据(实验1、实验2、实验3、实验4),对建立的燕尾榫节点M-θ力学模型的正确性进行验证。验证方式为:将文献中的实验数据代入到研究构建的模型中进行计算,并将计算值与实验结果进行对比。力学模型计算值M1c,M2c与实验数据M1t,M2t的关系如图4所示。
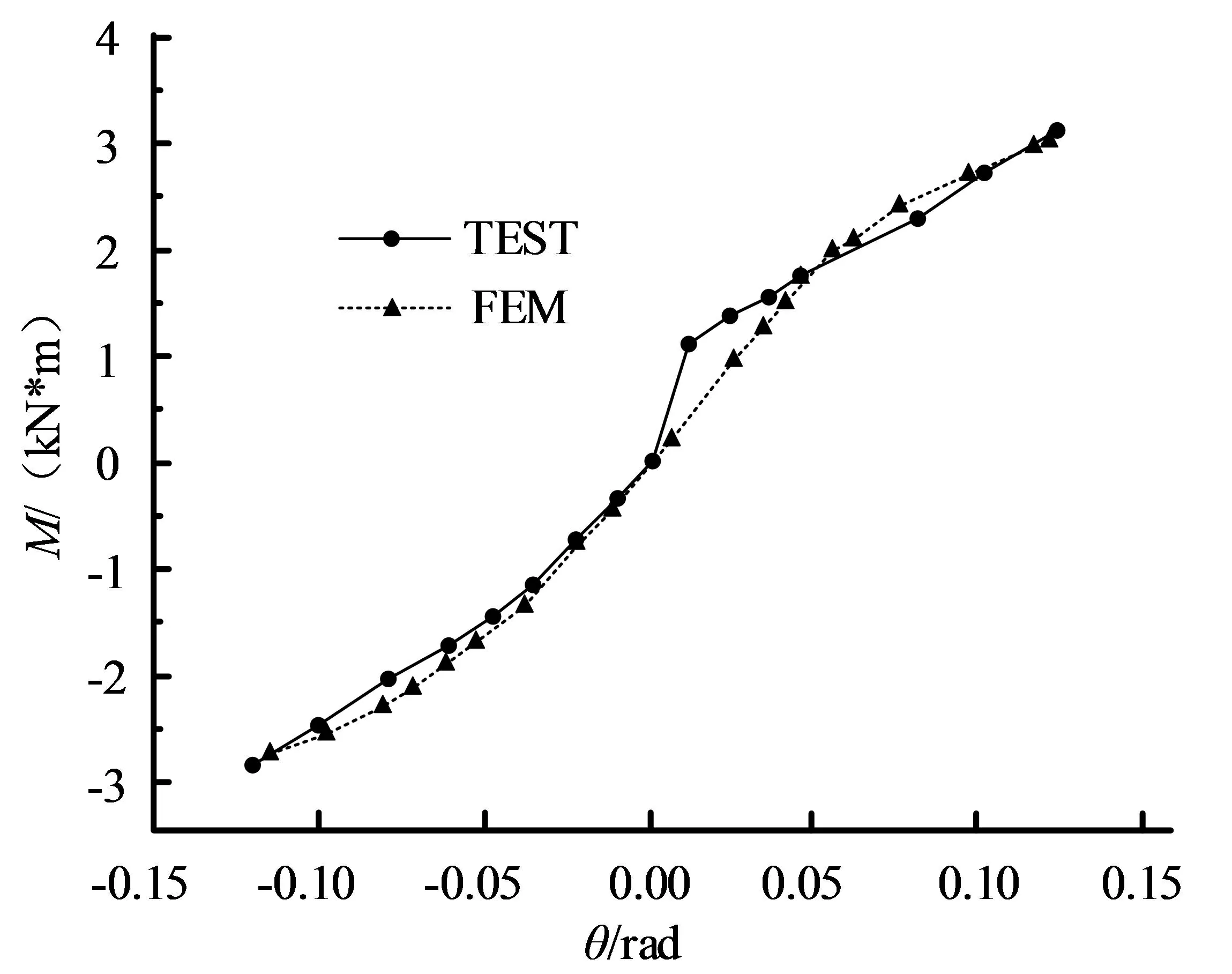
图3 燕尾榫数值模型验证

图4 燕尾榫节点力学模型的正确性分析
在图4(a)和图4(b)中容易看出,在将实验数据代入到建立的燕尾榫节点M-θ理论力学模型中后,模型的计算值与实验数据之间在弹性段和屈服段均吻合良好,在45°线附近。上述结果验证了所建立的燕尾榫节点M-θ理论力学模型的正确性。提取数值模型中燕尾榫柱架的的荷载-位移(P-Δ)的特征值并与实验值比较,结果如表3所示。

表3 P-Δ曲线的特征值
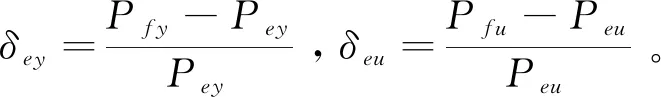
3 结 语
为分析古建木结构节点的抗震机理,并对其抗震性能进行评估,以燕尾榫为研究对象建立了理论力学模型。实验结果显示,模型的计算值与实验数据在弹性段与屈服段的吻合较好,在45°线附近,且根据模型计算获取各个特征值与实验数据的偏差均低于20%。综合以上研究结果表明,建立的燕尾榫力学模型具有较高的精度,能够为古建筑的修缮加固提供理论和数据支撑。此外,研究仅对燕尾榫进行了研究,未开展其它类型节点的探讨,这也是后续研究中需要着重注意的地方。

