单管通信塔脉冲型地震动强度参数研究

李波 李晓飞 王志江

摘要：以一典型的30 m高薄壁单管通信塔为研究对象，从太平洋地震工程研究中心（PEER）地震动数据中心选取50条近断层脉冲型地震动组成脉冲型地震动集。选取幅值参数、频谱参数、持时参数和能量参数4大类共14个地震动强度参数进行对比分析，从有效性和充分性两个维度得到在脉冲型地震动作用下最优地震动强度参数。结果表明：在同时考虑有效性和充分性的前提下，对于薄壁式单管通信塔，在脉冲型地震动作用下，地震动强度参数最优的是结构基本周期对应的谱加速度Sa（T1）和有效峰值加速度EPA。该结论可为薄壁式单管塔动力时程分析时选择最优地震动强度参数提供理论依据。

关键词：单管通信塔；脉冲型地震动；地震动强度参数；有效性；充分性

中图分类号：R315.9   文献标识码：A   文章编号：1000-0666（2023）02-0291-09

doi：10.20015/j.cnki.ISSN1000-0666.2023.0029

0 引言

通信系统是生命线工程系统的重要组成部分，截至2015年底，中国大陆移动通信用户数量已经达到13.06亿（阮左正等，2017），相应的基站通信鐵塔数量及其覆盖范围也急剧增大。作为通信天线的主要支撑体，通信铁塔的运行与否直接关系到整个通信系统的畅通。2018年四川汶川8.0级地震、2013年芦山7.0级地震以及2015年尼泊尔8.1级地震等震害调查均表明（《汶川特大地震抗震救灾志》编纂委员会，2015；刘爱文等，2012；刘金龙等，2013，2016），由于通信铁塔的破坏导致局部地区震后与外界通信联系中断，使救援工作不能及时有效地开展，从而造成巨大的人员伤亡和财产损失。

选取天然地震动对工程结构进行动力时程分析是结构抗震性能研究的主要手段之一，研究结果表明（Pan et al，2021；Tian et al，2017，2018；Amiri，Massah，2007），结构类型不同、地震动特性不同，适用于结构抗震性能研究的地震动强度参数（Intensity Measure，简称IM）也不同。对于格构式铁塔来说，比如输电塔和通信塔，目前，动力时程分析采用的地震强度参数主要有峰值加速度（PGA）（Pan et al，2021）、峰值速度（PGV）（Tian et al，2017）、结构基本周期对应的谱加速度Sa（T1）（Tian et al，2017；Amiri，Massah，2007）等。薄壁式的单管塔由于占地面积小、易于装饰成和环境相协调的造型，在市区较常见，但是对其进行地震作用下的动力响应分析时，应选取哪些最优地震动强度参数还鲜有研究，目前主要是借鉴房屋结构或者格构式铁塔取PGA或者Sa（T1）的研究居多，但其合理性还有待验证。

在理论研究和工程实践中，地震动强度一般由地震动强度参数进行量化表征，其中标量型参数主要包括幅值参数、频谱参数、持时参数和能量参数等（来庆辉等，2020；Baker，2006；吴文朋等，2020）。采用恰当的地震动参数来调整天然地震动，并选用合适的结构动力响应指标来评估结构损伤，有利于减少结构动力时程分析计算结果的离散性，提高计算效率。因此，选用合理的地震动参数对结构动力响应分析至关重要。另外，与普通地震动相比，近断层脉冲型地震动常有较宽的反应谱敏感区，由于其在短时间内会对结构产生很高的能量输入，故这类地震动对工程结构的潜在破坏力通常会更大（戴靠山等，2020；徐亚洲等，2020）。

本文选取《通信塔标准图集》（Q/ZTT 1002—2015）中的典型薄壁式单管通信塔为分析模型，50条近断层脉冲型地震动组成脉冲型地震动集。从幅值参数、频谱参数、持时参数和能量参数4个方面选取14个地震动强度参数进行对比分析，从有效性和充分性两个维度得到在脉冲型地震动作用下最优地震动强度参数，以期为薄壁式单管塔动力时程分析时选择最优地震动强度参数提供参考。

1 脉冲型地震动选取

近年来，与场地和地震断层之间相对位置密切相关的近场脉冲型地震动越来越受到结构工程领域学者的关注，近断层脉冲型地震动由于其主要能量发生在相对比较集中的时域或频域段，被普遍认为是导致各类工程结构产生严重破坏的关键因素。

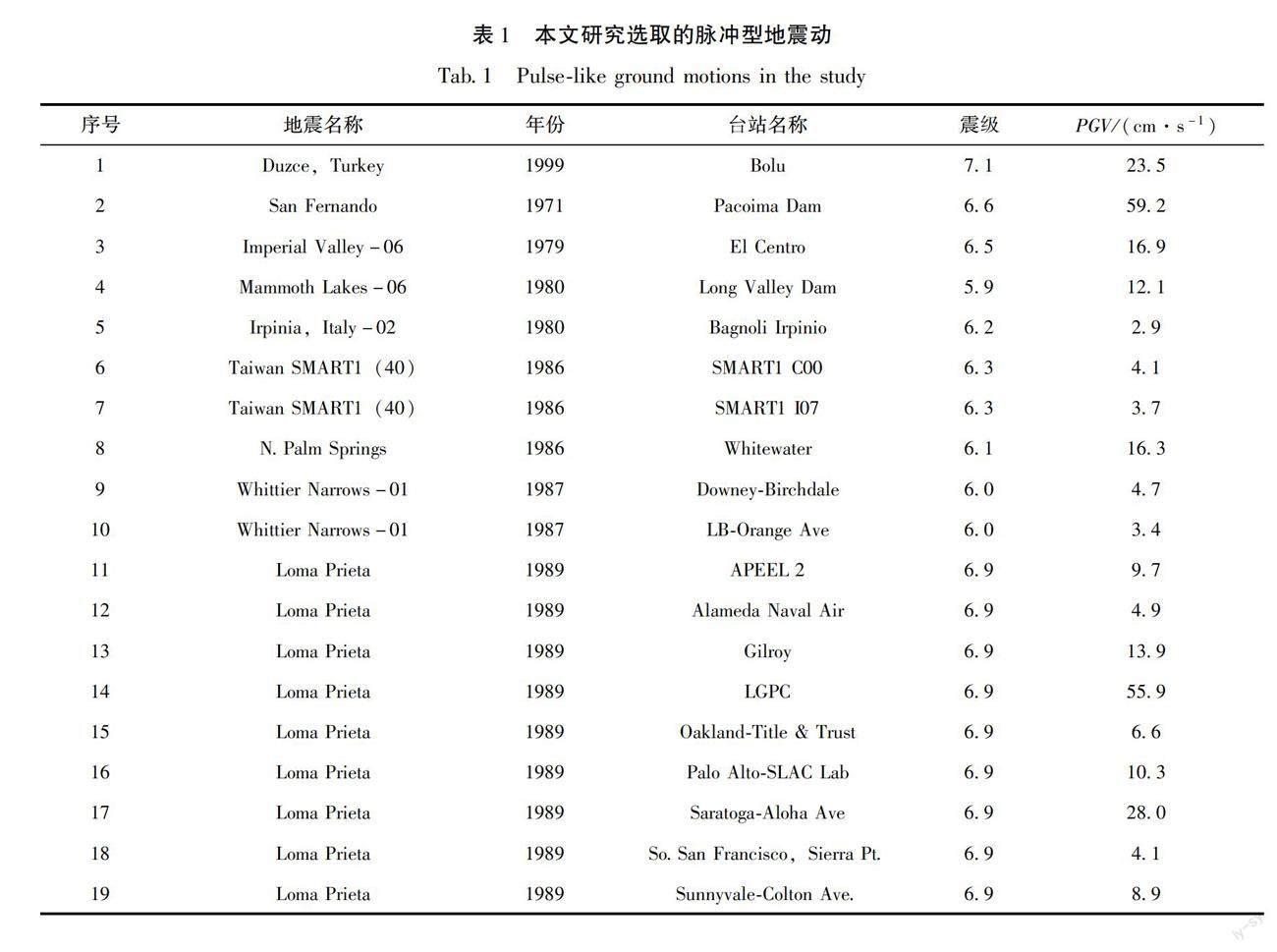
Zhai 等（2018）提出了一种简单有效的脉冲型地震动定量识别方法。该方法主要基于脉冲型地震动的固有特征，引入了有效速度半周期的概念，然后提出确定速度脉冲的一个有效指标——脉冲能量比EP，并根据有效速度半周数将地面运动分为几种类型，并为每种类型确定相应的EP阈值。本文依据该方法从PEER地震动数据中心选取50条近断层脉冲型地震动组成脉冲型地震动集，并采用贝叶斯云分析法（Bayesian cloud analysis）（Jalayer et al，2015）对结构进行分析。本文研究所选脉冲型地震动基本参数见表1，其地震动震级统计分布情况如图1所示。

2 地震动强度参数的选取

合理的地震动强度参数IM是预测结构响应和评估结构地震功能可恢复能力的重要基础，应反映结构地震响应指标或损伤指标。地震动强度参数的选取一方面要做到全面性，涵盖地震动三要素（幅值参数、频谱参数和持时参数），以及能量参数（来庆辉等，2020；Lai et al，2022；Baker，2006；Kazantzi，Vamvatsikos，2015），另一方面，应尽可能挑选物理意义明确、应用范围广、在地震工程中出现频次较高且有代表性的参数。本文所选取地震动强度参数不含矢量型参数，表2列出有代表性的地震动参数。

3 计算模型

3.1 单管塔概况及有限元模型

为了使分析对象具有代表性，本文从中国铁塔公司制定的《通信铁塔标准图集》中选取30 m高的薄壁式单管通信塔作为结构原型，采用有限元软件ABAQUS建立有限元模型，如图2所示。塔壁为Q345型钢，采用壳单元模拟，壳单元网格划分大小根据整体尺寸比例取0.58，阻尼比取2%。由于结构型钢的材料为非线性，根据理想弹塑性假定，材料屈服准则采用Von Mises准则，材料本构选用双折线本构模型，力学参数详见表3。塔顶端天线平台、避雷针以及各段螺栓、爬梯等作为集中荷载附加施加在各段水平节点处，单管塔底部固结。

3.2 模型验证

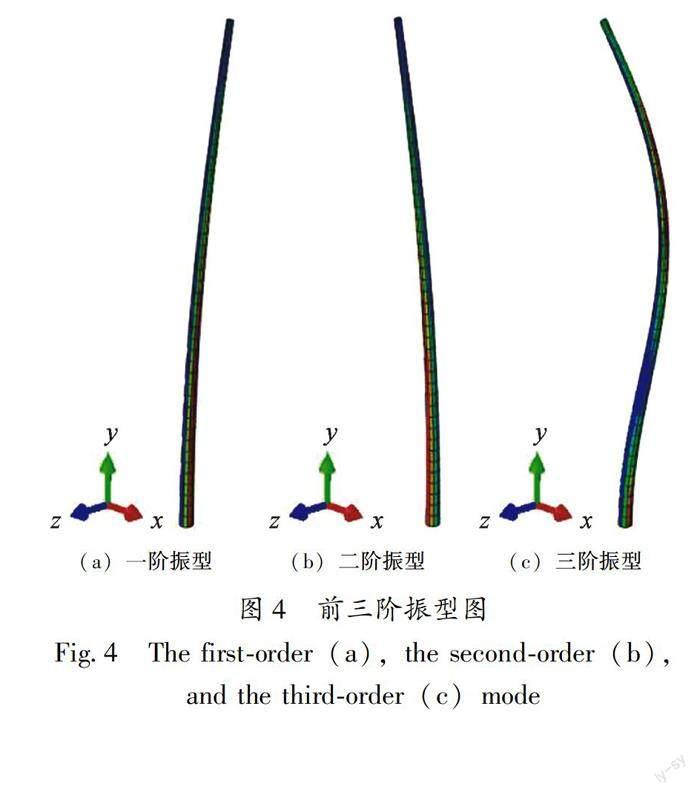
有限元模型的合理性直接关系到分析结果的可靠性，为了验证所建模型的合理性，笔者在黑龙江省哈尔滨市选取一个依据《通信铁塔标准图集》设计的30 m高单管通信塔（图3a）进行基频测试。该铁塔基础采用桩基且土质较硬，可近似等价于底部固定约束，在28 m高度处有一个天线支架，将三向加速度传感器布置在该高度。考虑到通信塔高度和供电条件等原因，需要得到两个水平方向和竖向的相关数据，仪器主要选取HCF400-A1型加速度仪，采样频率为100 Hz，对测试塔采3段数据，每段数据采样1 min，测得塔在环境激励下的加速度时如图3b所示，共有3组数据，第一组和第二组为互为垂直的两个水平方向的振动数据，第三组为塔的竖向振动数据。通过傅立叶变换得到频谱曲线如图3c所示。根据基本频率和第一周期之间的转换关系，得到原型结构和有限元模型基本周期见表4。前三阶模态质量参与系数分别为33.4%、33.4%和25.5%（自振频率分别为0.765 Hz、0.765 Hz和3.698 Hz），合计为92.3%，振型模态如图4所示。有限元模型和原型结构基本周期的差值在10%以内，表明本文基于ABAQUS軟件建立的单管通信塔有限元模型是合理可靠的。

3.3 结构响应

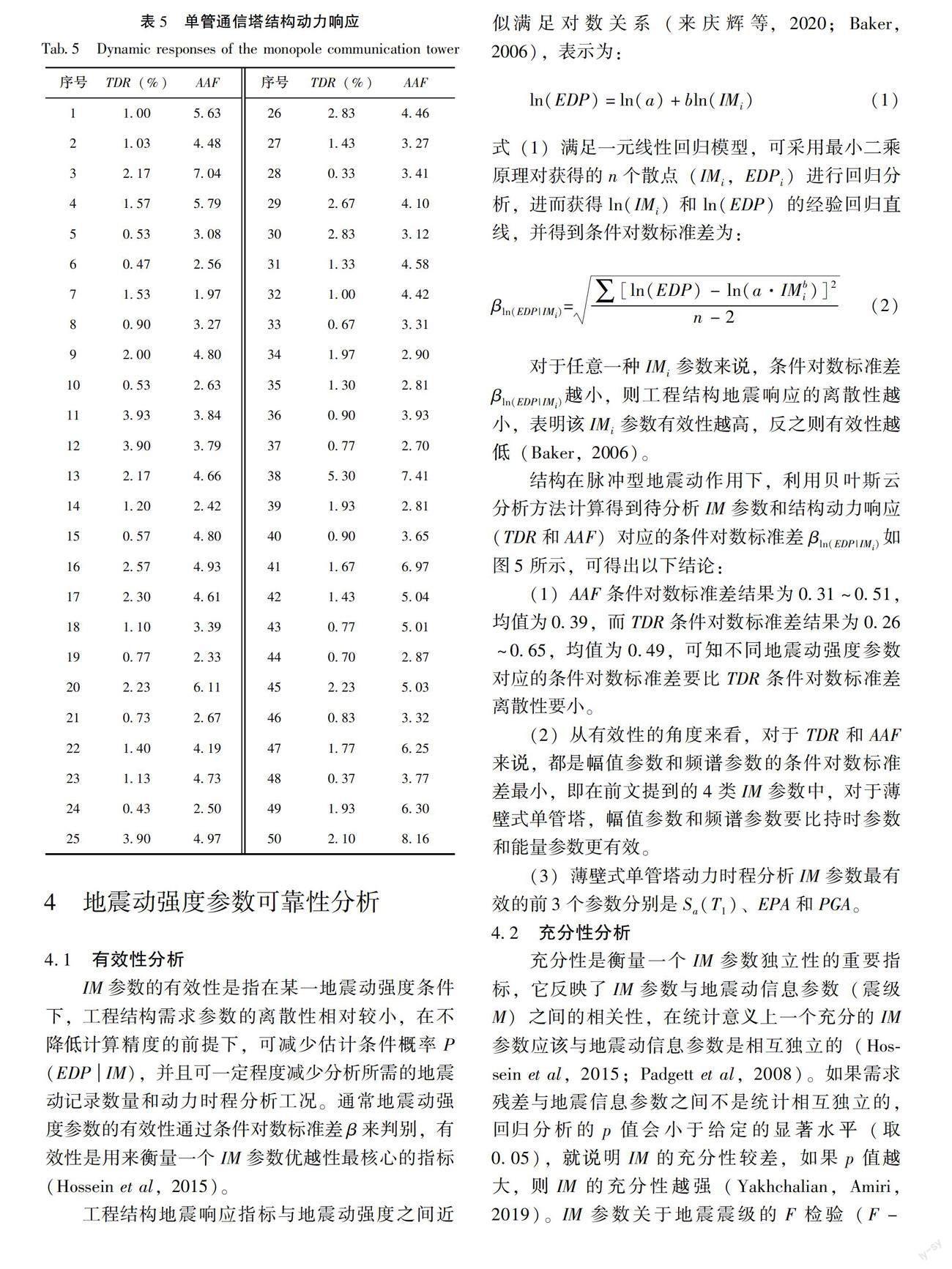
单管通信塔的作用在于支撑通信天线进行区域范围内信号的接收和传递，地震作用下单管塔的动力响应主要由自身塔顶相对于塔底水平向相对位移角（Top Drift Ratio，简称TDR）来衡量。另外，单管塔作为高耸型钢结构，在水平地震作用下，塔顶加速度放大效应较大，而通信天线和塔顶平台主要通过螺栓连接，塔顶放大之后的加速度将对连接的螺栓产生较大的动力响应，所以塔顶加速度放大系数（Acceleration Amplification Factor，简称AAF）也是重要的结构动力响应需求参数，故本文选用TDR和AAF作为工程需求参数（Engineering Demand Parameter，简称EDP）。本文所选取的单管塔在单向脉冲型地震动作用下的结构动力响应见表5。

4 地震动强度参数可靠性分析

4.1 有效性分析

IM参数的有效性是指在某一地震动强度条件下，工程结构需求参数的离散性相对较小，在不降低计算精度的前提下，可减少估计条件概率P（EDPIM），并且可一定程度减少分析所需的地震动记录数量和动力时程分析工况。通常地震动强度参数的有效性通过条件对数标准差β来判别，有效性是用来衡量一个IM参数优越性最核心的指标（Hossein et al，2015）。

工程结构地震响应指标与地震动强度之间近似满足对数关系（来庆辉等，2020；Baker，2006），表示为：

ln（EDP）=ln（a）+bln（IMi）（1）

式（1）满足一元线性回归模型，可采用最小二乘原理对获得的n个散点（IMi，EDPi）进行回归分析，进而获得ln（IMi） 和ln（EDP）的经验回归直线，并得到条件对数标准差为：

βln（EDP｜IMi）=∑［ln（EDP）-ln（a·IMbi）］2n-2（2）

对于任意一种IMi参数来说，条件对数标准差βln（EDP｜IMi）越小，则工程结构地震响应的离散性越小，表明该IMi参数有效性越高，反之则有效性越低（Baker，2006）。

结构在脉冲型地震动作用下，利用贝叶斯云分析方法计算得到待分析IM参数和结构动力响应（TDR和AAF）对应的条件对数标准差βln（EDP｜IMi）如图5所示，可得出以下结论：

（1）AAF条件对数标准差结果为0.31～0.51，均值为0.39，而TDR条件对数标准差结果为0.26～0.65，均值为0.49，可知不同地震动强度参数对应的条件对数标准差要比TDR条件对数标准差离散性要小。

（2）从有效性的角度来看，对于TDR和AAF来说，都是幅值参数和频谱参数的条件对数标准差最小，即在前文提到的4类IM参数中，对于薄壁式单管塔，幅值参数和频谱参数要比持时参数和能量参数更有效。

（3）薄壁式单管塔动力时程分析IM参数最有效的前3个参数分别是Sa（T1）、EPA和PGA。

4.2 充分性分析

充分性是衡量一个IM参数独立性的重要指标，它反映了IM参数与地震动信息参数（震级M）之间的相关性，在统计意义上一个充分的IM参数应该与地震动信息参数是相互独立的（Hossein et al，2015；Padgett et al，2008）。如果需求残差与地震信息参数之间不是统计相互独立的，回归分析的p值会小于给定的显著水平（取0.05），就说明IM的充分性较差，如果p值越大，则IM的充分性越强（Yakhchalian，Amiri，2019）。IM参数关于地震震级的F检验（F-test）得到的p值如图6所示。因为IM参数需同时满足有效性和充分性条件，故在充分性分析时，只需重点关注最有效的幅值参数和频谱参数即可，图6的结果表明：

（1）不同IM参数对应的TDR条件对数标准差均超过充分性显著水平限制。

（2）单管塔AAF条件对数标准差持时参数均小于0.05，表明持时参数和地震震级并非相互独立，而其它的幅值参数、频谱参数和能量参数对应的条件对数标准差均大于0.05，满足相互独立的条件。

（3）对最有效的幅值参数和频谱参数进行单管TDR和AAF二者的充分性排序，最满足充分性的前3个参数分别是Sa（T1）、EPA和PGV。

5 结论

本文以一典型的30 m高单管薄壁式通信塔为研究对象，基于贝叶斯云分析的方法，以地震动强度参数线性对数回归拟合的方法，从有效性和充分性两个维度来选取在脉冲型地震动作用下最优地震动强度参数，得出以下结论：

（1）從有效性的角度来看，对于薄壁式单管塔，铁塔顶点水平位移角和塔顶加速度放大系数都是幅值参数和频谱参数比持时参数和能量参数更有效。

（2）薄壁式单管塔动力时程分析潜在破坏势参数最有效的前3个参数分别是Sa（T1）、EPA和PGA。

（3）对最有效的幅值参数和频谱参数进行铁塔顶点水平位移角和加速度放大系数二者的充分性排序，最满足充分性的前3个参数分别是Sa（T1）、EPA和PGV。

综上分析可知，在同时考虑有效性和充分性的前提下，对于薄壁式单管通信塔，在脉冲型地震动作用下，地震动强度参数最优的是Sa（T1）和EPA。需要说明的是，本文考虑的均为标量型地震动强度参数，在后续的研究中，可进一步对比讨论矢量型地震动强度参数。

感谢江汉大学来庆辉博士对本文脉冲型地震动选取提供的理论指导和帮助！

参考文献：

戴靠山，周裕洲，李波，等.2020.近断层地震动对电厂主厂房的地震响应影响分析［J］.地震工程与工程振动，40（4）：8-16.

来庆辉，胡进军，谢礼立，等.2020.脉冲型地震动潜在潜在破坏势参数的相关性分析［J］.世界地震工程，36（1）：35-43.

刘爱文，厦珊，吕红山，等.2012.汶川地震极重灾区通信基站典型震害及原因分析［J］.电信工程技术与标准化，25（12）：82-86.

刘金龙，黄勇，喻绍宁.2016.尼泊尔8.1级地震通讯系统震害调查分析［J］.自然灾害学报，25（2）：146-151.

刘金龙，林均岐，刘如山，等.2013.芦山7.0级地震通讯系统震害调查分析［J］.自然灾害学报，22（5）：91-97.

阮左正，陈生年，李奎明.2017.铝合金三管通信塔研究［J］.轻金属，54（3）：42-45.

《汶川特大地震抗震救灾志》编纂委员会.2015.汶川特大地震抗震救灾志（卷四）：地震灾害志［M］.北京：方志出版社.

徐亚洲，田晓航，张慧，等.2020.近断层地震动作用下风机塔地震反应分析［J］.地震工程与工程振动，40（1）：57-66.

Amiri G G，Massah S R.2007.Seismic response of 4-legged self-supporting telecommunication tower［J］.IJE Transactions B：ApNo.ications，20（2）：107-126.

Baker J W.2006.Vector-valued ground motion intensity measures for probabilistic seismic demand analysis［D］.Stanford：Stanford University.

Hossein E，Jalayer F，Lucchini A，et al.2015.Preliminary ranking of alternative scalar and vector intensity measures of ground shaking［J］.Bulletin of Earthquake Engineering，13（10）：2805-2840.

Jalayer F，Derisi R，Manfredi G.2015.Bayesian cloud analysis：efficient structural fragility assessment using linear regression［J］.Bulletin of Earthquake Engineering，13（4）：1183-1203.

Kazantzi A K，Vamvatsikos D.2015.Intensity measure selection for vulnerability studies of building classes［J］.Earthquake Engineering and Structural Dynamics，44（15）：2677-2694.

Lai Q H，Hu J J，Xu L J，et al.2022.Method for ranking pulse-like ground motions according to damage potential for reinforced Concrete Frame Structures［J］.Buildings，12：754.https：//doi.org/10.3390/.

Padgett J E，Nielson B G，DesRoches R.2008.Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios［J］.Earthquake Engineering and Structural Dynamics，37（5）：711-725.

Pan H Y，Li C，Tian L.2021.Seismic fragility analysis of transmission towers considering effects of soil-structure interaction and depth-varying ground motion inputs［J］.Bulletin of Earthquake Engineering，19：4311-4337.

Tian L，Gai X，Qu B.2017.Shake table tests of steel towers supporting extremely long-span electricity transmission lines under spatially correlated ground motions［J］.Engineering Structures，132：791-807.

Tian L，Ma R S，Qu B.2018.Influence of different criteria for selecting ground motions compatible with IEEE 693 required response spectrum on seismic performance assessment of electricity transmission towers［J］.Engineering Structures，156：337-350.

Yakhchalian M，Amiri G G.2019.A vector intensity measure to reliably predict maximum drift in low-to mid-rise buildings［J］.Proceedings of the Institution of Civil Engineers-Structures and Buildings，172（1）：42-54.

Zhai C H，Li C H，Kunnath S，et al.2018.An efficient algorithm for identifying pulse-like ground motions based on significant velocity half-cycles［J］.Earthquake Engineering of Structure Dynamics，47（3）：757-771.

Study on Intensity Parameters of the Monopole Communication TowerSubjected to the Pulse-like Ground Motion

LI Bo1，LI Xiaofei1，WANG Zhijiang2

（1.School of Architecture Engineering，Binzhou University，Binzhou 256600，Shandong，China）

（2.Shandong Binzhou Urban Construction Group Co.Ltd.，Binzhou 256600，Shandong，China）

Abstract

The monopole communication tower is one of the main forms of the mobile communication tower.In this study，a typical 30-meter high monopole communication tower was taken as an example，and 50 pieces of near-fault，pulse-like ground motions were selected from the PEER Ground Motion Data Center to form a pulse-like ground motion set.A total of 14 ground motion parameters including amplitude parameters，spectrum parameters，duration parameters and energy parameters were selected for comparative analysis.The optimal ground motion intensity parameters of the monopole communication tower by the action of the pulse-like ground motion were selected in view of the effectiveness and sufficiency of the parameters.The results show that on the premise of effectiveness and sufficiency，for the monopole communication tower，the optimal intensity parameters are the spectral acceleration Sa（T1） corresponding to the basic period of the tower and the effective peak acceleration EPA.

Keywords：monopole communication tower；pulse-like ground motion；intensity parameters；effectiveness；sufficiency

收稿日期：2022-04-02.

基金項目：山东省自然科学基金面上项目（ZR2022ME209）；滨州学院实验技术项目（BZXYSYXM202016）.

第一作者简介：李 波（1988-），讲师，主要从事通信系统地震灾害模拟与预测研究.E-mail：libo20070025@126.com.

通讯作者简介：李晓飞（1988-），副教授，博士，主要从事生命线系统抗震研究.E-mail：lxf2011iem@126.com.

李波，李晓飞，王志江.2023.单管通信塔脉冲型地震动强度参数研究［J］.地震研究，46（2）：291-299，doi：10.20015/j.cnki.ISSN1000-0666.2023.0029.