非对称尾部相依视角下的金融机构系统性风险研究
王剑 杜红军

摘要:本文以我国45家上市金融机构为样本,分别使用12种非对称和4种对称Copula模型拟合“系统—机构”二元相依结构,对比基于最优非对称和最优对称Copula-广义CoVaR的估计精度,并从宏观金融和微观机构层面分析影响金融机构系统性风险的重要因素。结果表明:时变非对称尾部相依是“系统—机构”相依关系的普遍特征;我国金融业各子部门的系统性风险排序基本为“银行>保险>证券>多元金融”;金融机构的个体风险与系统性风险的相关性较弱,下尾相依性是识别系统重要性金融机构的关键因素;在危机期间,金融机构的杠杆率对个体风险和系统性风险具有显著的正向影响;稳定和改善宏观金融环境是化解系统性风险的根本举措。
关键词:非对称尾部相依;Copula;系统性风险;广义CoVaR
中图分类号:F832 文献标识码:A 文章编号:1007-0753(2023)03-0054-16
一、引言
党的二十大报告明确指出“要强化金融稳定保障体系,依法将各类金融活动全部纳入监管,守住不发生系统性风险的底线”。2021年中央经济工作会议提出“要正确认识把握和防范化解重大风险,完善金融风险处置机制”。这预示着中国特色宏观审慎金融政策的进一步落实和深化。
随着我国金融改革的不断推进,金融机构逐步由“分业经营”向“混业经营”过渡,金融创新和影子银行规模的不断扩张既提高了金融服务的普惠性,同时也加强了金融机构间的业务往来和關联资产重叠。另外,移动互联网的高速发展、信息媒介的不断更迭使得金融市场内的信息传递效率显著提高,进而加深了我国金融网络的紧密度。
自2008年全球金融危机爆发以来,关于系统性风险的普遍认识开始从“太大而不能倒”向“太关联而不能倒”转变(Chen等,2020),人们逐渐意识到忽视金融机构间的关联性而采取孤立的微观审慎监管政策是这场危机的诱因之一。李政等(2016)通过构建我国40家上市金融机构的格兰杰因果网络,发现自2012年以来我国金融机构间的总体关联性呈上升趋势。蒋海和张锦意(2018)使用LASSO分位数回归技术构建了我国上市银行尾部风险网络,发现银行间尾部风险网络的关联性对系统性风险具有正向影响。胡利琴等(2018)则发现银行资产的高同质性、创新关联和银行网络集中度会显著提高银行风险的外溢性。显然,关联性特征正逐渐成为金融机构系统性风险研究中不可忽视的因素。
防范化解系统性风险的前提是准确度量和预测金融机构的系统性风险水平。传统的风险计量方法如“在险价值(VaR)”和“期望损失(ES)”侧重于个体风险的测度,而忽视了风险的外溢性。Tobias和Brunnermeier(2016)率先考虑到银行个体风险的负外部性,创造性地提出了“条件在险价值(CoVaR)”模型,通过分位数回归捕捉金融机构与金融系统间的尾部依赖,并辅以宏观状态变量进行动态估计。肖璞等(2012)首次将基于分位数回归的CoVaR模型应用于我国银行业,用来识别我国系统重要性银行。高国华和潘英丽(2011)则基于DCC-GARCH模型对CoVaR进行估计,并分析了影响我国银行系统性风险的机构层面因素。越来越多的证据表明金融变量间的尾部相依性具有时变、非线性和非对称特征,然而CoVaR模型忽视了金融机构更极端的风险情形,因此基于传统分位数回归或GARCH模型的CoVaR测度方法可能严重低估金融机构的系统性风险水平。近年来,Copula模型因其对多元分布建模的灵活性被广泛应用于联合风险计量和系统性风险研究,Chen和Khashanah(2016)结合Copula模型与Mainik和Schaanning(2014)提出的广义CoVaR模型测度了美国10部门间的风险传染效应。Reboredo和Ugolini(2016)应用GARCH-Copula-广义CoVaR模型研究了原油价格和全球主要股指在不同分位点上的相依关系和风险溢出强度。江一帆(2021)基于GARCH-Copula-CoVaR模型测度了中国与“一带一路”沿线国家股市间的风险溢出效应。潘德春和曾建新(2022)则基于时变SJC Copula-CoVaR模型测度了我国股票市场与基金市场间的尾部风险溢出效应。为了更好地估计尾部风险,Zhu等(2021)结合Copula模型与EVT极值理论测度了在金融危机和新冠肺炎疫情期间美国能源部门和农业部门间的尾部风险溢出效应。考虑到金融机构与金融系统相依结构和尾部相依性的时变特征,赵林海和陈名智(2021)使用滚窗法动态拟合多种Copula模型,测度了我国33家金融机构的系统性风险贡献。此外,为检验广义CoVaR的估计精度,王锦阳等(2018)采用严格的后验分析验证了基于Copula模型估计广义CoVaR的准确性。
首先,本文分别使用12种非对称和4种对称的静态或时变参数Copula模型拟合我国45家金融机构与金融系统的相依结构,并依据多种准则进行模型优选,这一方面避免了大部分已有研究直接设定Copula模型带来的主观性偏差,另一方面也避免了滚窗动态估计造成的信息损失;然后,结合EVT极值理论估计各机构在最优Copula模型下的广义CoVaR并对相关风险指标进行后验回测;最后,根据系统性风险的大小给出金融机构的系统重要性排序,并从宏观金融和微观机构层面分析影响金融机构系统性风险的重要因素。
本文的主要贡献包括以下三个方面:第一,使用多种Copula模型依据多种准则拟合“系统—机构”相依结构的最优模型,使得估计出的广义CoVaR更为公允有效;第二,使用Kupiec回测对比基于最优非对称和对称Copula模型下的广义CoVaR估计精度,通过统计手段验证了金融机构与金融系统间非对称的尾部相依结构特征;三是从宏观金融和微观机构层面分析了影响金融机构系统性风险、个体风险以及下尾相依性的重要因素。
二、研究设计
(一)广义CoVaR
若给定金融系统s收益率序列Rs和金融机构i收益率序列Ri,VaR被定义为一定置信水平q下金融系统(机构)可能面临的最大损失,即
三、实证分析
(一)数据说明和描述性统计
本文选取2012年10月22日至2022年9月8日我国金融业4个子行业45家上市金融机构的股票收盘价数据作为样本。根据申万行业分类,包含16家银行机构、20家证券机构、4家保险机构和5家多元金融机构。为保证时间间隔的连续性,以样本期内交易日为基准日期,对因停牌而缺失的数据使用前一交易日数据插补,并计算各样本金融机构的日对数收益率。为减小误差,收益率均用百分数表示,即
表1列示了各子行业代表性金融机构②收益率序列的描述性统计③,可以发现:工商银行的标准差最小而国网英大的标准差最大,表明银行机构股价波动较小而多元金融机构股价波动较大;各序列偏度异于0、峰度大于3且JB检验均在1%的水平下显著,表明各序列分布呈有偏且“尖峰厚尾”的非正态特征,其中国网英大的负偏度和峰度最大,表明多元金融机构的股价具有较高风险;ADF检验均在1%水平下显著,表明各序列均平稳,Q(20)和ARCH检验均显著,表明各序列均存在自相关性和条件异方差性。因此适合使用ARMA(1,1)-GJR-EVT模型拟合金融机构负对数收益率序列的边缘分布并估计对应的VaR值。
(二)边缘分布与VaR值的估计结果及回测
表2列示了部分金融机构使用ARMA(1,1)
-GJR-EVT模型拟合负对数收益率序列边缘分布的估计结果。在Panel B中,各序列Leverage(杠杆项)的系数均显著为正,表明各类金融机构股价波动的杠杆效应显著;在Panel C中,工商银行广义Pareto分布的形状参数最大而中信证券最小,表明银行机构股价序列具有更显著的“厚尾”特征。
估计所有样本金融机构95%置信水平(下同)下的VaR值并进行回溯测试,表3列示了所有金融机构VaR值估计序列的回测P值,结果均大于0.05即接受原假设,表明各金融机构VaR的估计结果较为准确,进一步说明边缘分布的拟合结果较优。
(三)基于非对称Copula函数的相依结构估计与优选
构造“系统—机构”二元收益率序列(Rs|-i,t, Ri,t)。为避免金融机构i与金融系统s的收益率序列存在伪相关,参考Karimalis和Nomikos(2018)的方法,使用剔除金融机构i后其余样本金融机构前一交易日的市值占比为权重,计算加权平均系统收益率:
为更好地捕捉金融机构与金融系统收益率间非对称的相依结构,本文选取Gumbel、Rotated Gumbel(下文简写为RG)、Clayton、Rotated Clayton(下文简写为RC)、BB7和SJC这6种具有非对称相依结构的Copula函数所对应的静态和时变(TVP)参数模型对不同金融机构与金融系统间的相依结构进行估计,并依据多种准则通过“投票”④进行模型优选。表4列示了各金融机构最优非对称Copula模型的优选结果,可以发现:所有金融机构均选择时变(TVP)Copula模型,表明金融机构与金融系统普遍存在时变的尾部相依性;不同金融机构的最优Copula模型不尽相同,表明不同金融机构与金融系统的相依结构存在异质性;所有金融机构的Copula模型均选择具有双尾相依性的TVPBB7或TVPSJC模型,表明金融机构与金融系统间普遍既存在极端上行联动也存在极端下行联动。
(四)基于最优非对称Copula模型的CoVaR估计及回测
基于表4中的优选模型,本文估计各金融机构的CoVaR并进行回溯测试。表5列示了所有金融机构在最优非对称Copula模型下的CoVaR估计序列的回测P值,结果均大于0.05即接受原假设,表明对所有样本金融机构基于最优非对称Copula模型的估计结果准确。
(五)基于最优对称Copula模型的CoVaR估计及回测
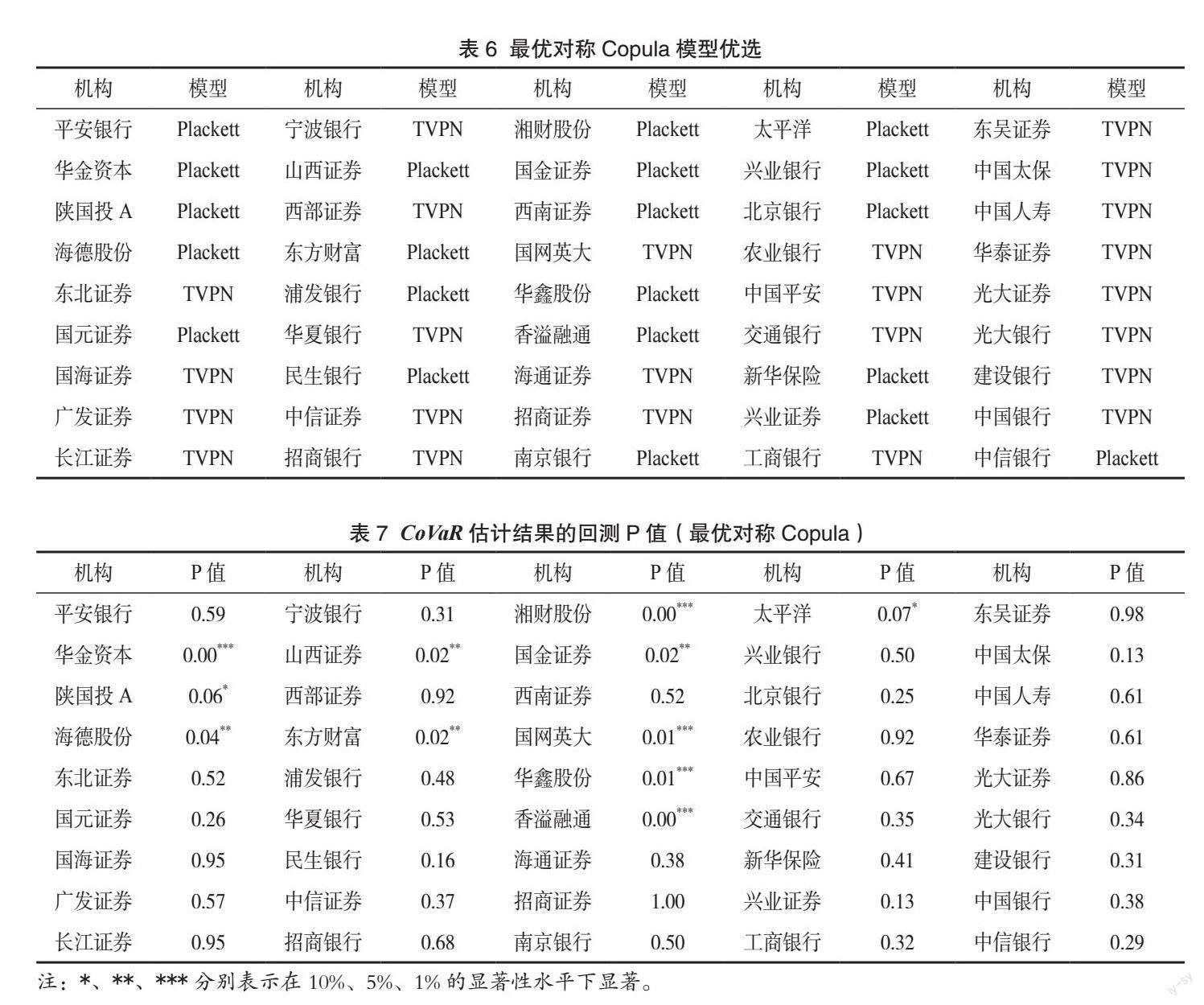
为说明非对称Copula模型相较于对称Copula模型更能真实准确地反映金融机构与金融系统的相依结构,进一步基于4种具有对称结构且无尾部相依特征Copula函数的静态或时变参数模型估计样本金融机构与金融系统的相依结构,包含正态Copula(Normal)、時变正态Copula(TVPN)、Plackett和Frank。表6列示了各金融机构的最优对称Copula模型的优选结果,大部分金融机构选择TVPN为最优,表明大部分金融机构与金融系统间具有时变的相依性。表7列示了各金融机构基于最优对称Copula模型CoVaR估计序列的回测P值,其中以华金资本为首的11金融机构CoVaR估计序列的回测P值至少在10%的水平下拒绝原假设,表明部分金融机构在对称相依结构的假设下CoVaR估计结果的准确性较差。
综上,具有非对称尾部相依特征Copula函数的时变参数模型对于拟合我国金融机构与金融系统间相依结构的效果更优,一方面说明我国金融机构与金融系统间普遍存在时变非对称的尾部相依结构,另一方面说明基于时变非对称Copula模型计量我国金融机构的系统性风险更为准确有效。
(六)系统性风险的计算
本文使用AMRA(1,1)-GJR-EVT模型计算剔除金融机构i后金融系统s的VaR值,并结合各金融机构基于最优非对称Copula模型估计的CoVaR计算各金融机构的系统性风险(ΔCoVaR)、上尾部相依性(DepU)和下尾相依性(DepL)。
1. 截面维度分析
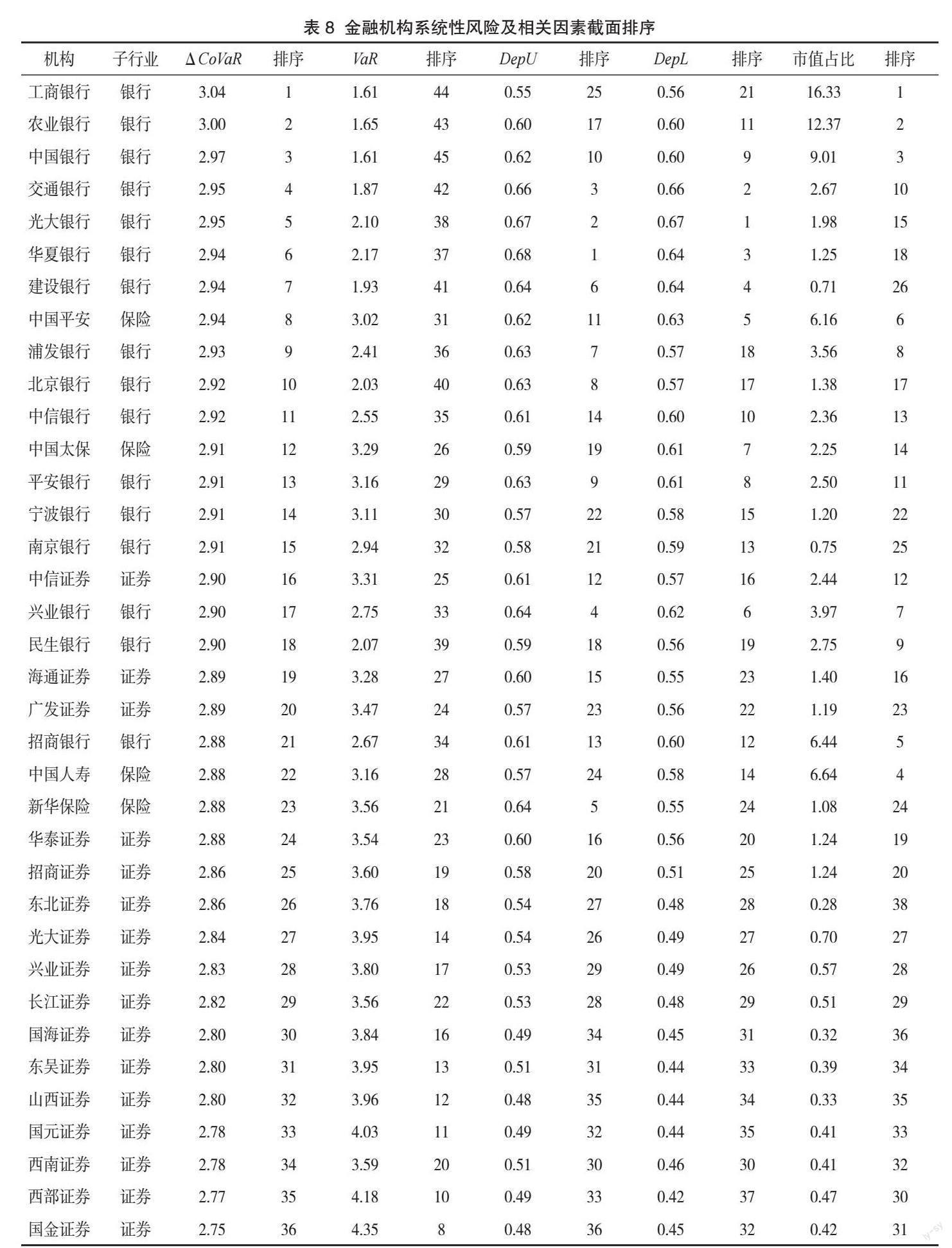
取各样本金融机构的ΔCoVaR、VaR、DepU、DepL和市值占比在样本期内的平均值并进行截面排序,各项指标的排序结果如表8所示。以ΔCoVaR的排序为基准,总体来看系统性风险在各类金融机构中的大小排序基本为:银行>保险>证券>多元金融。前10位中银行类机构占9位,其中五大国有银行中有4家位居前5,表明银行类机构在我国最具有系统重要性,国有银行是我国系统性风险的主要贡献者。VaR与ΔCoVaR排序偏离较大,表明金融机构的个体风险与系统性风险相关性较弱,而DepU、DepL与ΔCoVaR的排序较为类似,同时市值占比和ΔCoVaR的排序相似度较高,表明“系统—机构”的尾部相依性以及金融机构的规模与其系统性风险具有较高的正相关关系。为验证上述观点,基于截面数据,将ΔCoVaR对VaR、DepU、DepL和市值占比进行回归,回归结果如表9所示。由表可知,VaR的系数不显著而DepL的系数显著为正,表明在截面维度,金融机构的个体风险与系统性风险没有显著的相关性,而“系统—机构”下尾相依性与金融机构的系统性风险存在显著正相关,进一步说明“系统—机构”下尾相依性对系统重要性金融机构具有显著的识别作用。
2.时序维度分析
将风险变量(ΔCoVaR、VaR和DepL)分别在截面维度上取平均得到各变量的平均时序,如图1所示。可以发现,ΔCoVaR和VaR的趋势高度重合,表明金融机构的个体风险与系统性风险具有时序关联性;各风险变量在几次经济危机期间(2013年银行“钱荒”、2015年“股灾”、2020年新冠肺炎疫情)的总体平均水平均高于其他时期,表明宏观经济危机对金融机构的系统性风险、个体风险以及下尾相依性产生显著冲击。为进一步考察我国金融业各子部门风险变量在时序维度上的差异,本文计算出各风险变量在各子部门中的截面均值。如图2所示,各子部门的ΔCoVaR在时序上排序为:银行>保险>证券>多元金融,而各子部门的VaR排序则与ΔCoVaR相反,即“多元金融>证券>保险>银行”。各子部门的DepL排序与ΔCoVaR相同,其中银行类和保险类机构与金融系统间的下尾相依性远高于证券类和多元金融类机构。
综合截面和时序维度的分析结果可以发现:尽管银行和保险类机构具有较低的个体风险,但由于其与金融系统间的下尾相依性较高,银行类和保险类机构具有较高的系统性风险。反之,多元金融类机构的个体风险较高,但由于其与金融系统间的下尾相依性较弱,其系统性风险较低。由此可知,金融机构与金融系统间的下尾相依性是影响金融机构系统性风险的重要因素,而个体风险的影响则较弱。
四、系统性风险的影响因素分析
为进一步探究金融机构系统性风险的影响因素,本文分别从宏观金融层面和微观机构层面分析影响金融机构系统性风险、个体风险和下尾相依性的重要因素。
(一)宏观金融因素的影响分析
本文以金融机构的风险变量(系统性风险ΔCoVaR、个体风险VaR和“系统—机构”下尾相依性DepL)为被解释变量对一系列宏观金融变量进行前瞻性面板回归分析,滞后期分别设为5天、10天和15天。回归模型如下:
其中,k为滞后期,u为个体固定效应,Cri为虚拟变量,在危机期取值为1,否则为0。结合我国近年来发生的重大金融风险事件和图1中系统性风险相关指标的时序特征,将危机期设定为2013、2015、2020年。选取如下宏观金融变量:Rm为沪深300指数日对数收益率,用于反映A股的整体收益水平;Vm为沪深300指数年化波动率,用于反映A股的整体波动水平;ctb为3个月期国债利率的一阶差分,用于反映将资金投资于股市的机会成本;cts为10年期国债利率减3个月期国债利率差的一阶差分即期限利差的变化,衡量收益率曲线斜率的变化,用于反映市场参与主体对市场未来的预期和信心;ls为3个月期SHIBOR减3个月期国债利率即TED利差,用于反映市场流动性风险的大小;ccs为10年期AAA级企业债利率减10年期国债利率差的一阶差分即信用利差的变化,用于反映市场信用风险的大小;err为沪深300房地产业收益率减沪深300金融业收益率即房地产行业超额收益率,用于反映房地产市场的火热程度。所有方程均使用机构层面的聚类标准误估计。模型中还纳入了各宏观金融变量与危机期虚拟变量的交乘项(Rmt-kCri、Vmt-kCri、ctbt-kCri、ctst-kCri、lst-kCri、ccst-kCri、errt-kCri)。
表10列示了宏觀金融因素对金融机构不同风险变量在不同滞后期的回归结果,整体来看,各宏观金融变量对金融机构风险变量的影响系数基本显著,表明宏观金融因素对金融机构的系统性风险、个体风险和“系统—机构”下尾相依性均具有显著影响。
具体而言,由表10第(1)列宏观金融因素对ΔCoVaR的回归结果可知:当滞后期k=5时,除errt-k的系数在1%的水平下显著为负外,其余宏观金融变量的系数均在1%的水平下显著为正,表明在非危机期,A股整体收益上行、整体波动加剧、资金机会成本上升、市场预期和信心增强、市场流动性风险和信用风险上升都会提高金融机构的系统性风险,而房地产行业市场的繁荣能显著降低金融机构的系统性风险。Rmt-kCri、ctbt-kCri、ctst-kCri的系数均在1%的水平下显著为负且其绝对值均大于Rmt-k、ctbt-k、ctst-k的系数,表明在危机时期,A股整体收益上行、资金机会成本上升以及市场预期和信心增强能降低金融机构的系统性风险,这是由于在危机时期,A股整体收益上升以及市场预期和信心增强降低了因市场恐慌而导致风险集中爆发的可能性,而资金机会成本上升则能有效抑制市场投机行为,进而降低市场的潜在风险。Vmt-kCri、lst-kCri、errt-kCri的系数显著为正,表明危机期放大了市场波动和流动性风险对金融机构系统性风险的正向影响,同时危机期房地产市场的过度繁荣所导致的房地产泡沫也更容易加剧金融机构的系统性风险。由表10第列(2)、(3)列可知:部分变量系数的符号在不同滞后期发生改变,表明部分宏观金融因素对金融机构系统性风险的长期影响具有时变特征。
由表10第(4)列宏观金融因素对VaR的回归结果可知:当滞后期k = 5时,其回归结果与以ΔCoVaR为被解释变量的结果基本一致,区别在于相较于后者,ccst-kCri的系数显著为负,表明政府部门和金融机构在危机期所采取的风险缓释措施一定程度缓解了市场信用风险对金融机构个体风险的正向影响。由表10列第(5)、(6)列可知:所有在5%水平下显著的宏观金融变量系数在不同滞后期的符号基本一致,表明宏观金融因素对金融机构个体风险的长期影响较为稳定。
由表10列(7)宏观金融因素对DepL的回归结果可知:当滞后期k=5时,ctbt-k、ctst-k、lst-k、ccst-k的系数均在1%水平显著为负,而errt-k的系数在1%水平显著为正,表明在非危机期资金机会成本上升、市场预期和信心增强、流动性风险和信用风险上升均能降低“系统—机构”间的损失联动性,而房地产市场的繁荣强化了“系统—机构”间的损失联动性。Rmt-kCri、errt-kCri的系数在1%水平显著为负,而ctbt-kCri、ctst-kCri、ccst-kCri的系数在1%水平显著为正,表明在危机期股市整体收益上行、房地产市场繁荣能降低“系统—机构”间的损失联动性,但危机期也强化了资金机会成本、市场预期和信心以及信用风险对金融机构系统性风险的正向影响,这是由于在危机期股市整体收益上行和房地产市场繁荣能够降低整个金融市场下行的可能性,但同时资金机会成本的上升也加大了市场投资者的实际经济损失,而市场预期和信心的增强提高了投资者的主动风险承担意愿,信用风险上升则增大了企业的违约概率,进而提高了“系统—机构”间的损失联动性。由表10第(8)、(9)列可知:所有在5%水平下显著的宏观金融变量系数在不同滞后期的符号基本一致,表明宏观金融因素对“系统—机构”下尾相依性的长期影响较为稳定。
综上,基于宏观金融因素对金融机构不同风险变量在不同滞后期的回归结果,可以得出以下几点结论:第一,宏观金融因素对金融机构的系统性风险和个体风险的影响机制较为类似,危机期强化了市场波动、流动性风险和房地产泡沫对金融机构个体风险和系统性风险的正向影响。第二,宏观金融因素对“系统—机构”下尾相依性的作用效应倾向于在危机期表现为正向影响,此时资金成本上升、市场预期增强、信用风险加剧将提高“系统—机构”间的损失联动性。第三,宏观金融因素对金融机构系统性风险的长期影响具有时变特征,对个体风险和“系统—机构”下尾相依性的长期影响则较为稳定。
(二)微观机构因素的影响分析
本文以金融机构的风险变量为被解释变量,对滞后一期的微观机构变量进行面板回归分析,选取年度微观机构变量,年度风险变量通过年内聚合转频得到。回归模型如下:
其中,Cri为危机期虚拟变量,u为个体固定效应。本文选取如下微观机构变量:Voli,t-1表示金融机构股票的年化波动率,用于反映金融机构股票的波动情况;Betai,t-1表示金融机构的股票beta值,用于反映金融机构股价面临的系统风险;Sizei,t-1为金融機构总资产的对数值,用于反映金融机构的规模;Levi,t-1为金融机构的权益乘数,用于反映金融机构的杠杆水平;RoAi,t-1表示金融机构的资产收益率,用于反映金融机构的盈利能力;BMi,t-1表示金融机构股票的账面市值比,用于反映金融机构股票的投资价值。所有方程均使用机构层面的聚类标准误估计,模型中还纳入了各微观机构变量与危机期虚拟变量的交乘项(Voli,t-1Cri、Betai,t-1Cri、Sizei,t-1Cri、Levi,t-1Cri、RoAi,t-1Cri、BMi,t-1Cri)。为避免异常值干扰,对所有微观机构变量在其样本分布的1%和99%位置进行缩尾处理。
表11列示了微观机构变量对金融机构不同风险变量的回归结果,整体来看,大部分微观机构变量的统计显著性较弱。相较于宏观金融因素,微观机构因素对金融机构系统性风险、个体风险和“系统—机构”下尾相依性的影响较弱。
具体而言,从微观机构变量对ΔCoVaR的回归结果来看,Betai,t-1的系数在1%水平下显著为正,表明金融机构股票的系统风险对金融机构的系统性风险具有显著的正向影响。Levi,t-1Cri的系数在1%水平下显著为正,表明在危机期,金融机构的高杠杆将加剧金融机构的系统性风险。BMi,t-1Cri的系数显著为负,表明在危机期,金融机构股票的投资价值越高,其系统性风险水平越低,这是由于越具有投资潜力的金融机构其基本面状况越好,经营也越稳健。
从微观机构变量对VaR的回归结果来看,Levi,t-1的系数在1%水平下显著为正,表明金融机构的杠杆率对个体风险具有正向影响,同时Levi,t-1Cri的系数在1%水平下显著为正,表明危机期进一步放大了高杠杆对金融机构个体风险的促进作用。BMi,t-1Cri
的系数在1%水平下显著为负,表明在危机期,金融机构越具有投资价值,其个体风险越低。
从微观机构变量对DepL的回归结果来看,Voli,t-1的系数在1%水平下显著为正,表明金融机构股票的波动率对“系统—机构”下尾相依性具有正向影响,Levi,t-1Cri的系数在1%水平下显著为负,表明在危机期,金融机构提高杠杆能降低“系统—机构”的下尾相依性。
综上,基于微观机构因素对金融机构不同风险变量的回归结果,可以发现:相较于宏观金融因素,微观机构因素对金融机构系统性风险、个体风险和“系统—机构”下尾相依性的影响较弱;在非危机期,金融机构股票的系统风险对其系统性风险具有正向影响,金融机构的高杠杆提高其个体风险,金融机构股票波动加剧提高了“系统—机构”下尾相依性;危机期加剧了杠杆率对金融机构个体风险和系统性风险的正向影响,但此时金融机构杠杆率的提高能降低“系统—机构”下尾相依性。
五、结论与建议
本文旨在从相依结构的拟合优度和系统性风险的估计精度两个方面验证我国金融机构与金融系统间的非对称尾部相依关系,并在此基础上分析了影响我国金融机构系统性风险的重要因素。具体而言,本文以我国45家上市金融机构为样本,分别使用12 种非对称和4种对称Copula模型拟合“系统—机构”二元相依结构,对比基于最优非对称和最优对称Copula模型广义CoVaR估计值的后验精度,给出我国金融机构的系统重要性排序,并从宏观金融层面和微观机构层面分析了影响金融机构系统性风险、个体风险和“系统—机构”下尾相依性的重要因素。根据上述分析,本文得出以下结论:
第一,时变非对称尾部相依是我国金融机构“系统—机构”相依关系的普遍特征。
第二,我国金融机构的系统性风险排序基本为“银行>保险>证券>多元金融”。此外,“系统—机构”下尾相依性是识别系统重要性金融机构的重要因素,而金融机构的个体风险与系统性风险的相关性较弱。
第三,根据金融机构系统性风险的影响因素分析结果可以发现:相较于微观机构因素,宏观金融因素对银行系统性风险的影响更为显著;在非危机期,杠杆率监管仅能降低银行的个体风险,而在危机期,杠杆率监管能有效降低银行的个体风险和系统性风险。
根据以上结论,为维护我国金融稳定和防范系统性金融风险,提出如下政策建议:
第一,考虑到我国金融机构与金融系统普遍存在时变非对称尾部相依关系,金融监管部门应实时监测金融机构间的尾部风险联动,提高系统重要性金融机构的风险警戒线,防止系统重要性金融机构因尾部事件引发系统性金融危机。
第二,考虑到金融业不同子行业的风险特征区别明显,金融监管部门在逐步提高监管效率的同时仍应坚持分业监管模式。就银行类机构而言,其个体风险较低,却是我国系统性金融风险的主要贡献者,这是由于长期以来银行是我国金融体系的核心组成部分,庞大的资产规模和稳健的经营战略使得银行通过各种复杂且多元化的表内外业务分散了个体风险,但与此同时也加深了其在金融网络中的关联重要性。近年来金融脱媒和银行业竞争的加剧对银行业的稳定造成了冲击,因此金融监管部门在积极推动银行业务转型的同时也应该严控其通过金融创新、影子银行和通道业务进行监管套利,防范这些行为造成系统性风险隐患。
第三,考虑到“系统—机构”下尾相依性与金融机构系统性风险的正向关系,金融监管部门应抑制金融机构间的损失联动,一方面严格执行逆周期监管政策,防止金融機构在经济上升期的风险积聚,另一方面严格控制金融机构的同业依赖,在经济下行期减小破产风险在金融机构间的传染效率。
第四,从长远角度来看,防范和化解系统性金融风险的根本举措是稳定和改善宏观金融环境。相关部门应着力于创造良好的金融市场秩序,构建完善的金融法律体系,维持稳定的宏观经济政策,减少由不确定性冲击导致的系统性金融危机。
注释:
① 为便于表述,后文所提及的CoVaR均为广义CoVaR。
② 以样本金融机构的平均市值大小排序为基准,选取各子行业规模最大的金融机构为例。
③ 由于篇幅所限,未列示所有机构收益率序列的描述性统计,如有需要向作者联系。
④“投票”:对不同金融机构与金融系统的相依结构建模,以NLL(负对数似然值)、AIC、BIC、HQ、平方欧氏距离和KS统计量最小为准则选择Copula模型,被各准则选择的模型获一票,最后综合得票最多的为最优Copula模型。
参考文献:
[1] CHEN Y, HU J, ZHANG W. Too connected to fail? Evidence from a Chinese financial risk spillover network[J]. China & World Economy, 2020, 28(06):78-100.
[2] 李政, 梁琪, 涂晓枫.我国上市金融机构关联性研究——基于网络分析法[J].金融研究,2016(08):95-110.
[3] 蒋海, 张锦意.商业银行尾部风险网络关联性与系统性风险——基于中国上市银行的实证检验[J].财贸经济,2018,39(08):50-65.
[4] 胡利琴, 胡蝶, 彭红枫.机构关联、网络结构与银行业系统性风险传染——基于VAR-NETWORK模型的实证分析[J].国际金融研究,2018(06):53-64.
[5] TOBIAS A, BRUNNERMEIER M K.CoVaR[J].The American Economic Review,2016, 106(07):1705-1741.
[6] 肖璞, 刘轶, 杨苏梅.相互关联性、风险溢出与系统重要性银行识别[J].金融研究,2012(12):96-106.
[7] 高国华, 潘英丽.银行系统性风险度量——基于动态CoVaR方法的分析[J].上海交通大学学报,2011, 45(12):1753-1759.
[8] CHEN K H, KHASHANAH K. Analysis of systemic risk: A vine copula-based ARMA-GARCH model[J]. Engineering Letters, 2016, 24(03): 268-273.
[9] MAINIK G, SCHAANNING E. On dependence consistency of CoVaRand some other systemic risk measures[J]. Statistics & Risk Modeling, 2014, 31(01): 49-77.
[10] REBOREDO J C, UGOLINI A. Quantile dependence of oil price movements and stock returns[J]. Energy economics, 2016, 54: 33-49.
[11] 江一帆.基于Copula函数的“一带一路”沿线地区金融风险相依性研究[J].金融经济,2021,545(11):33-41.
[12] 潘德春,曾建新.信息冲击下的金融市场尾部相依结构与风险溢出效应——以股票市场和基金市场为例[J].区域金融研究,2022,599(06):70-77.
[13] ZHU B, LIN R, DENG Y, et al.Intersectoral systemic risk spillovers between energy and agriculture under the financial and COVID-19 crises[J].Economic Modelling,2021, 105: 105 651.
[14] 赵林海, 陈名智.金融机构系统性风险溢出和系统性风险贡献——基于滚动窗口动态Copula模型双时变相依视角[J].中国管理科学,2021,29(07):71-83.
[15] 王锦阳, 刘锡良, 杜在超.相依结构、动态系统性风险测度与后验分析[J].统计研究,2018,35(03):3-13.
[16] GIRARDI G, TOLGAERG?N A. Systemic risk measurement: Multivariate GARCH estimation of CoVaR[J].Journal of Banking & Finance, 2013,37(08): 3 169-3 180.
[17] DUMOUCHEL W H. Estimating the Stable indexα in order to measure tail thickness: A critique[J]. Annals of Statistics, 1983, 11(04):1 019-1 031.
[18] 张连增, 胡祥. Copula的参数与半参数估计方法的比较[J].统计研究, 2014,31(02):91-95.
[19] PATTON A J. Modelling asymmetric exchange rate dependence[J]. International Economic Review, 2006, 47(02):527-556.
[20] KARIMALIS E N, NOMIKOS N K. Measuring systemic risk in the European banking sector: A Copula CoVaR approach[J]. The European Journal of Finance, 2018, 24(11):944-975.
(责任编辑:张艳妮/校对:唐诗柔)

