促进思维进阶的中考数学专题复习教学模型的建构与实施
武丽虹 葛余常
摘 要 中考数学专题复习是课堂教学的重要形式,但检视当下初中数学专题复习教学,还存在概念零散化、应用随意化、训练浅表化、手段陈旧化等思维进阶障碍。基于教学实践,积极探索学生“自探—自悟”、教师“促探—促悟”双线并进的思维进阶教学活动模式,促进专题复习教学改进。
关 键 词 思维进阶 专题复习 中考数学
引用格式 武丽虹,葛余常.促进思维进阶的中考数学专题复习教学模型的建构与实施[J].教学与管理,2023(13):34-36.
数学专题复习是让学生从整体上系统地对所学知识、数学思想方法进行聚合,以模块或单元展开进行教学的一种课型[1]。中考数学专题复习是课堂教学中促进学生知识内化、能力活化、素养优化的重要抓手,但实施专题复习教学的实际情况尚不尽人意,不能完全促进学生落实知识、发展能力、提高素养。为此,本文积极探索促进思维进阶的初中数学专题复习教学改进。
一、专题复习中思维进阶障碍的表现
1.概念零散化,思维缺乏整体性
专题复习应系统规划复习和训练的内容,做到主次分明、重点突出、横向联系、纵向贯通,不应是基本知识的简单重复。但一些教师还热衷于知识的“灌输”“平移”,没有把学生所学的局部的、零散的知识纵横联系形成整体结构,没有在更高层次上对学生所学的重点、难点知识进行内化,未能指向知识形成过程,这样只能使学生对课本中的知识“原生态”地保留与简单应用,难以打通学生已有知识技能、思维方法、经验策略与问题解决之间的通道。
2.应用随意化,思维缺乏敏捷性
复习离不开解题,但并不在于各种解法的罗列,更重要的是要揭示原理,能够让学生有带得走的经验。在专题复习中,不少教师不能将教材学习内容转化为复习教学材料,缺乏教学互动。教师不能给学生思维驻足的时空,学生只能被动接受知识;不能给予学生任何实质性指导以帮助学生消除盲点、清除堵点、突破难点,使学生失去独立思考和深入探究的机会;不能利用解题引导学生将所学知识内化迁移,学生失去学习兴趣;不能利用学习评价去导向、激励、改进学生的学习。
3.训练浅表化,思维缺乏深刻性
在专题复习过程中重视知识的落实,加强学生的知识储备是无可厚非的。但不少教师在专题复习中,受固有经验程式的影响,不能强化活动和体验,鲜少帮助学生把符号化的知识“打开”和将静态的知识“激活”,所开展的还是“常规、常讲、常练”的教学方式,满足于“识记、理解、应用”的浅层学习,导致“常考常错”现象屡屡发生。专题复习在关注知识和技能的同时,要指向能力发展过程,注重学生学习思维深度提高,促进学生在学习进阶中学会同中求异、异中求同、由此及彼、举一反三,从而提高学生的思维品质和学科素养。
4.方式陈旧化,思维缺乏创新性
培养学生信息素养是“互联网+”时代赋予学科教学的一项新使命。用技术来推动学习方式的变革,是目前教育信息技术应用主流。但实际操作中不少教师思维固化在传统的专题复习课堂上,成为大量陈述性知识和程序性知識的持有者和重复者,忽视学生原有的认知图式,缺少对学生变通思维、发散思维、创新思维等思维能力的培养,导致学生在涉及高阶思维的学习活动中表现并不尽人意。因此,应积极变革课堂教学形态,促进学生思维创新,努力帮助学生学会学习,从而提高学生综合素养。
二、促进思维进阶的教学模型建构
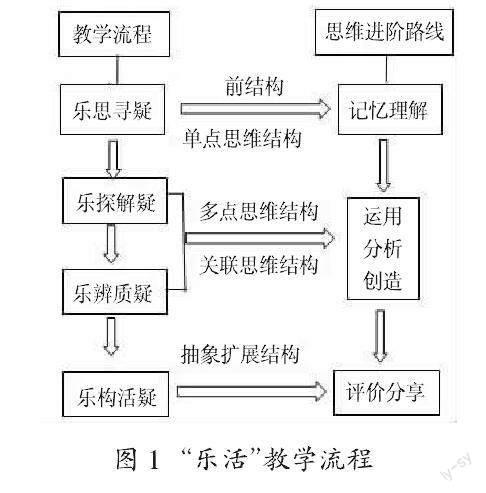
美国心理学家布鲁姆(Broome)将认知领域的教育目标由低到高分为六个层次:三种低阶思维(记忆、理解、运用)和三种高阶思维(分析、评价、创造)。香港大学比格斯教授基于可观察的学习结果的结构对学生思维进行分类,将学生思维结构分为低阶思维(前结构、单点思维结构、多点思维结构)和高阶思维(关联结构、抽象扩展结构)。发展学生的高阶思维需要教师在学生思维跃升的节点加以引导,基于深度教学与学科育人的本然统一,在根植课堂教学改进的常态教研中,积极探索促进低阶思维向高阶思维进阶的初中数学“乐活”课堂教学模式,凸显以“疑”为切口、以“探辨”为手段、以“活”为宗旨、以“技术”为辅助的“乐活”教学流程(如图1),从而将立德树人的根本任务落实到数学教学改进中,真正实现数学学科的育人价值。
三、中考数学专题复习教学模型的实施策略
针对目前教学过程中存在的浅层学习问题,教师应着力做学生思维进阶的引导者。积极探索学生“自探—自悟”、教师“促探—促悟”双线并进的思维进阶教学活动模式,为促进数学素养整体提高的课程实施提供教学改进新范式。
1.乐思寻疑——思维进阶切入点
高阶思维是思维进阶的目标导向。而思维进阶虽然需要教师的协助引导,但更关键的是需要学习者本身的深度思考。因此,教学中应设计富有挑战的问题,既让不同层次的学生都能基于自身已有学习经验解决问题,又能作为学生思维进阶的“跳板”。通过引发学生充满张力的思考,激发学生思维活力,助推学生思维从低阶向高阶爬坡,从而实现学生思维深层发展。
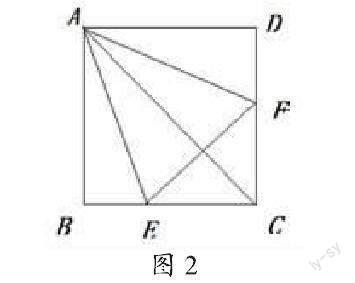
活动1:如图2,将边长为a的正方形纸片ABCD折叠,使边AB、AD都落在对角线AC上,展开后得折痕AE、AF,连接EF。
(1)你能得到哪些特殊的角或三角形?
(2)你能用a的代数式表示△CEF的周长吗?
专题复习首先要精心选择源题,通过追根溯源着力引导学生自主思考,激活学生思维。活动1中的折叠操作能加强学生学习体验,为学生打开直观想象提供路径,同时合理设计具有梯度的开放性问题,其目的是以任务驱动让学生经历操作、观察、想象与探究等思维活动,促进正方形知识的深层理解和整体建构。教师通过对图形有关结论的追问,打开学生思维心扉,加强正方形与三角形知识的关联,进一步培养学生逻辑思维能力。
2.乐探解疑——思维进阶立足点
问题是思维的核心。教师应当通过合适的问题、合理的方式为学习者搭建学习支架,启发、引导、帮助学生实现思维深度对话。并在知识的新奇处、学习的困惑处、活动的体验处、情感的共鸣处、经验的积累处从旁协助,从而延展并外化学生的思维路径,帮助学生经历过程构建知识、化解难点发展能力、内化方法提升素养。
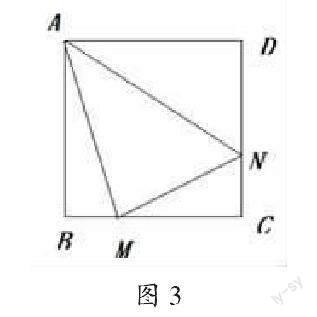
活动2:将图2中∠EAF绕点A旋转,使它的两边分别交BC、CD于点M、N,连接MN(如图3)。
(1)此时△CMN的周长是否改变?为什么?
(2)点A到MN的距离是否改变?为什么?
(3)你还能发现什么结论?
活动2是活动1的延续,设计问题链引导学生积极思考由此及彼、由例到类,促进学生思维从单点结构向多点结构和关联结构进阶。通过开放性问题让学生置身思维发散场,培养学生联想、类比、迁移等思维能力,从而提升学生思维的深度、精度和敏锐度。学生在活动中自主探究分析问题、解决问题并提出问题。
活动3:在以上活动基础上,过点M作MG⊥AM交CD于H,交AN的延长线于点G,设BM=m(如图4)。
(1)求CH、CN;
(2)求S△AMN:S△MN;
(3)你还能提出什么问题?
活动3在活动2基础上引发学生思维形成关联结构。通过线段设参,加强图形直观、逻辑推理和数学运算,丰富学生知识内涵。为学有余力的学生提供进阶路径,发展学生有高阶思维参与的理解性学习,培养学生结构化思考、批判性思维、创造性思维等优秀思维品质,让学生在思维深处体验更多精彩。
3.乐辨质疑——思维进阶着力点
专题复习课堂改进应从“教师中心”向“学生中心”转变。积极改造和重构知识发现和创生方式,为学生在认知发展的关键处提供可靠的脚踏点和支撑点,帮助学生在思维从“此阶”向“彼阶”不断攀登过程中质疑辨理,促进学生思维方式从简单的理解应用迈向分析、评价和创造,进而实现思维品质的进阶,促进学生思维形成关联结构和抽象拓展结构等高阶思维结构。
活动4:在图3中,连接BD分别交AM、AN于点P、Q(如图5)。
(1)BP、PQ、QD三条线段之间有怎样的关系?并说明理由。
(2)PQ与MN之间有怎样数量关系?并说明理由。
(3)连接MQ,你又能发现什么结论?
学习需要阶段性跳跃,通过精心安排能打破学科知识与知识边界的活动,进行活动关联与知识融通,启发学生开放思维、质疑思考,习得数学的眼光、思维与表达[2],促进学生知识、能力的迁移。经历拾级而上的思维训练,使学生借力打通初中几何图形各知识模块的隔断墙,沟通知识单元之间的内外联系,从课堂之点辐射到课后之面,促使碎片化的知识系统化、整体化、结构化。
4.乐构活疑——思维进阶制高点
发展学生的核心素养需要教学积极转型,教师应通过疑探灵动的活动设计,以开放性、建构性的任务支架帮助学生建立对正方形知识的前理解和后建构,助推学生疏通堵点、破解难点、强化重点、解决疑点,真正实现为“思维进阶”而教。
活动5:评价与分享:
(1)本节课我们研究了……
(2)我们经历了哪些过程?用到哪些方法?
(3)通过本节课的学习,你有什么新的想法?
高阶思维根植于学科核心素养,内化于学科学习活动,体现学科关键能力,蕴藏情感态度和价值观念[3]。问题设计着力学生“已知”“未知”“习得”过程,感悟知识的逻辑性、整体性和关联性。通过“乐构”,帮助学生重建知识、完善结构、促进迁移,助推学生学得更深入、更全面、更合理[4]。借助“活疑”,生发新观点、引发新认识、获得新评价,从而让数学高阶思维在体验和分享中真正创生。
专题复习是学生能力发展的助推器。在学科育人视域下,教师要围绕兴趣激发和潜能开发进行专题复习教学创新,积极探索思维进阶的路径和评价。通过设置具有一定程度的开放性、发散性、思考性和思辨性的问题,充分挖掘数学学科思想、拓展学生的思维深度和广度,让学生在复习过程中乐学、活学,进而培养高阶思维能力,提高复习效率。
参考文献
[1] 李君,葛余常.基于混合式学习的初中数学专题复习教学改进策略[J].江苏教育,2021(51):62-66.
[2] 武丽虹.指向学科关键能力的数学活动教学改进[J].中國数学教育,2021(11):12-16.
[3] 陈珍妮,吴仁芳.数学高阶思维的基本蕴涵、教育价值及培养途径[J].教学与管理,2022(06):64-68.
[4] 武丽虹,李君.育人指向的“小结与思考”的教学改进:以“代数式”中“小结与思考”为例[J].中学数学杂志,2022(04):24-27.
【责任编辑 郭振玲】

