基于线性Radon变换的超声混叠信号分离研究

聂 彬, 赵英亮, 聂鹏飞, 王黎明

(1.中北大学 信息探测与处理山西省重点实验室 山西 太原 030051;2.中北大学 信息与通信工程学院, 山西 太原 030051)

0 引 言

在火箭发动机燃烧厚度变化测试的场景中, 采用一发一收低频反射超声方法对此类大厚度介质进行测厚实验时, 所获得的信号结果中有效的底面回波信号与直达干扰信号产生混叠, 加大了分辨难度。同时, 在各项无损检测中, 如何对混叠信号进行有效分离处理一直是亟待解决的重点。

目前, 针对混叠信号进行的分离处理主要是对信号在时频域表现出的差异性进行进一步的分离。通过傅里叶分析可将时域内复杂难辨的混叠信号转换为频率域中简单信号的和, 从而分辨其频谱特征, 分数傅立叶变换(FRFT)方法[1-3]是在这一基础上进行了改进。后续信号处理过程中常用滤波器对已知频谱特性的混叠信号进行分离, 其中, 维纳滤波器具有处理重叠信号的潜力, 且常与反褶积算法结合以提高分辨率[4]。匹配追踪(MP)[5-8]作为超声信号分析中常用的一种方法, 是根据信号的时域特性构建原子字典对信号模型进行迭代求解, 常与稀疏反褶积结合用于重叠回波的处理中[9-11], 但该方法仅在解决单个回波问题中具有其独特的优越性[12]。

借助于日趋成熟的深度神经网络, Arthur等[13]利用超声回波信号在时域表现出的形状和振幅等特征来训练卷积神经网络以达到对重叠超声回波的识别和分离。深度学习方法虽能分离信号, 但在处理幅度较小的混叠回波时, 仍然存在固定偏差[14]。盲源分离法作为一种传统的分离技术[15]被广泛应用, 黄珊等[16]利用EFICA算法对信号进行了盲分离, 然而, 该方法在实际操作过程中仍存在源信号无法估计和对应的混叠模型无法确定的弊端。

对诸如火箭发动机等大厚度介质进行测试采集和处理后的单个回波信号无论在时域还是在频域上, 特征均无明显差别。前文所述重叠回波处理方法主要针对信号在时域和频域所表现出的明显差异进行分离处理, 并不能很好地适用于这种大厚度检测场景。然而, 对大厚度介质进行测厚所得的多条信号在时空上表现出不一样的特性, 即: 直达干扰信号呈现规律一致性, 而有效底面回波信号呈现区别于直达干扰信号的推移差异性。根据这一特点, 本文从二维角度出发, 通过分析信号数据的时空特点, 将结合线性Radon变换的自适应相减算法应用于大厚度工件超声重叠回波信号的处理中, 通过仿真实验数据的对比分析, 验证了该方法的实用性和有效性, 为分离时频域差异不明显的信号提供了新思路。

1 基于线性Radon变换的自适应相减

由于回波信号数据不同时间获取的信号有振幅、相位、频率及走时上的差异, 为了校正这些误差, 需要将预测的干扰波模型应用到滤波算子中, 使得经过滤波算子处理后的预测干扰波与原始回波数据经过作差后能量最小, 也就是要求有效波能量最小。基于这一原理, 本文引入基于L2范数的自适应相减方法并对其进行了扩展。本文将信号转换至线性Radon域进行自适应相减处理, 借助线性Radon变换具有可将在时空域呈线状分布的数据分别进行映射投影汇聚的性能, 可进一步提高自适应匹配的精度。

1.1 L2范数自适应相减算法

采集到的超声信号由表面杂波、噪声干扰和有效波组合而成, 为方便对超声回波阵列进行处理, 引入经典的最小二乘自适应相减算法[17], 即基于L2范数的自适应相减算法。常规的最小二乘自适应相减算法基于有效信号能量最小假设, 将该方法进行拓展可得到2D自适应相减算法的数学模型

Ds=S-D0f,

(1)

式中:Ds表示经过相减处理的有效波数据阵列;S表示原始信号数据阵列;D0表示杂波干扰信号构建的数据矩阵;f表示2D匹配滤波算子。

匹配滤波器f的设计目标是使得设定的杂波干扰信号数据经过滤波器后与原始数据的杂波干扰差异达到最小, 从而经过相减得到底面回波信号, 由此引入能量最小化。

(2)

对f进行求导并令值等于0, 可得f的最小二乘解

f=(D0TD0+ε2I)-1D0TS。

(3)

为提高整体计算过程的稳定性, 在式(3)中引入了单位矩阵I, 阻尼因子ε通常为一常数, 起到提高矩阵求逆过程中算法稳定性的作用。

1.2 基于线性Radon变换的自适应相减

由于杂波干扰信号呈现出与有效波信号相异的规律分布, Tau-p变换(线性Radon变换)可将规律分布的杂波信号数据和有效信号数据分别进行映射投影汇聚, 从而便于后续自适应相减处理。给定一条积分路径t=τ+φ(p,x), 则线性Radon变换的正反变换为

(4)

(5)

式(4)为正变换, 式(5)为反变换,d(t,x)为输入变量,m(τ,p)为输出变量, 当φ(p,x)=px时, 即为线性Radon变换的表达式, 其中,p为直线斜率,τ为截距时间。

在实现过程中, 需要将积分形式表示为离散求和的形式, 根据线性Radon变换具有的时不变特性, 结合傅里叶变换将线性Radon变换转换到频率域进行计算, 可写成矩阵相乘形式, 即

D=LM,

(6)

式中:D表示数据矩阵;L表示线性Radon变换频率域的转换因子矩阵;M表示经过线性Radon变换的数据矩阵。那么, 最小二乘(LS)意义下线性Radon变换的矩阵表达式为

M=(LTL+βI)-1LTD,

(7)

式中:β为阻尼因子, 起到防止计算过程出现奇异值的作用, 一般取值在0.01～1之间;I为单位矩阵。

将采集到的原始信号数据S及杂波信号数据D0构建为式(7)的矩阵D, 通过线性Radon变换可将采集到的原始信号及杂波信号从时间域转换至Radon域, 即可得到Radon域的原始信号数据St和杂波干扰信号数据D0t, 将其代入式(1)中, 得到Radon域的自适应相减公式为

Dst=St-D0tft,

(8)

式中:Dst表示Radon域自适应相减后的信号数据;ft为Radon域的匹配滤波算子。

利用有效底面回波和杂波在Radon域中表现出来的分布差异, 进行自适应相减, 可达到从原始数据中分离出有效底面回波信号的目的。

2 仿真实验数据处理

构建如图1 所示的被测模型几何结构, 设定模型为均匀介质, 超声传播速度为1 600 m/s。被测几何模型共包含5个厚度不同的阶梯层, 初始阶梯层厚度最薄层(5号厚度阶梯)设置为68 mm, 相邻两个厚度阶梯层的厚度差设置为10 mm, 依此类推。设置换能器1和2构成一个换能器组, 换能器1和2分别为激励换能器和接收换能器, 换能器间距设置为8 cm。将整个换能器组沿图1中箭头所示方向移动并采集信号, 以模拟实际实验场景。鉴于高斯模型在超声信号模拟中的普适性, 在仿真模拟实验中采用如式(9)所示的高斯超声波信号模型。

图1 被测模型结构图

s(t)=γe-α(t-τ)2cos(2πfc(t-τ))+n(t),

(9)

式中:γ为信号幅值系数;α为信号带宽因子;τ为延时时间;fc为信号中心频率;n(t)为高斯白噪声。设γ=1,α=2×109Hz,fc=50 kHz,τ根据图1不同厚度反射波三角几何关系单独设置, 则几何关系式为

(10)

式中:h为不同阶梯的厚度;l为换能器间距;v为超声传播速度。

在上述模型的基础上增加对应的杂波干扰信号, 由此可得到构建的杂波干扰模型D0和原始信号数据S。如图2 为通过模拟获取的3号阶梯未加噪的原始信号波形, 可明显看到杂波与有效信号产生混叠。

图2 3号阶梯未加噪的原始信号波形

对所构建的模型添加30 dB的高斯白噪声以模拟实际中存在的噪声, 对仿真模型在t-x域直接运用自适应相减算法处理, 结果如图3(b)所示。引入线性Radon变换, 将原始数据和杂波模型转换至Radon域, 设置参数p为0.000 001, 参数x为0.2, 在Radon域进行自适应相减, 得到处理后的结果并进行对比, 如图3(c)所示。图中, 每一个阶梯包含10条信号, 如信号数1～10表示第一个阶梯采集到的信号, 依此类推。

图3 仿真数据处理结果对比

选择有效波与杂波产生较大相交混叠的5号阶梯厚度进行波形对比, 以分析比较两种处理手段的分离效果。为方便分析, 截取0.05 ms～0.25 ms的信号进行波形对比, 结果如图4 所示, 由图4 可以看出, 由于算法特性, 经过变换后的波形能量整体发生了压制。

图4 5号厚度阶梯仿真数据处理结果波形对比

根据图3 和图4 可知, 经过仿真数据初步测试, 直接对信号数据进行自适应相减处理和在Radon域对信号数据进行自适应相减处理均能够在一定程度上压制直达干扰信号, 还原出有效信号, 已经达到了算法要求的结果。

为进一步比较直接对信号数据进行自适应相减和结合线性Radon变换进行自适应相减的信号处理效果, 将每个厚度阶梯层的厚度减小50 mm, 以加大杂波干扰信号和有效信号的混叠程度, 并对大程度混叠信号数据进行处理, 得到如图5 所示的结果对比能量图。同样, 截取5号厚度阶梯的信号的0 ms～0.25 ms以方便分析, 波形对比如图6 所示。

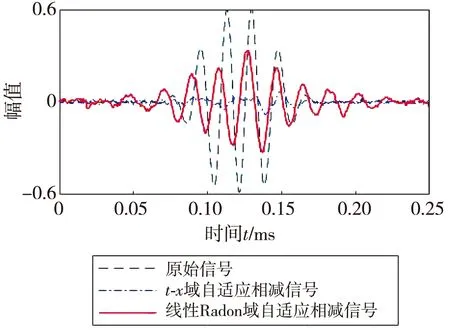
图6 大程度混叠情况下5号厚度阶梯仿真数据处理结果波形对比

由于直达干扰波和有效波之间形成相交, 尤其在大程度混叠情况下, 自适应相减算法失去了压制直达干扰波的效力, 相比直接对数据模型进行自适应相减, 结合线性Radon变换的自适应相减法能够很好地压制直达干扰部分, 并还原出了有效信号数据。

利用超声反射几何关系, 对经过结合线性Radon变换的自适应相减处理分离的不同厚度的有效信号进行厚度反推解算, 结果如表1 所示。

表1 模型厚度反推解算结果

由表1 可以看出, 经过处理后的厚度结果与实际厚度数据接近, 绝对误差≤0.7 mm, 相对误差≤0.65%。综上分析, 区别于直接进行自适应相减的方法, 结合了线性Radon变换的自适应相减方法能够起到压制直达干扰波并分离出有效信号的作用, 通过对仿真数据的实验测试, 验证了该方法在大厚度介质低频超声信号分离处理领域的适用性。

3 实验数据处理

为了更准确地验证该算法的实用性, 对大厚度模型进行点火检测实验。实验中, 采用多通道超声仪器产生超声激励信号, 50 kHz低频超声换能器发送和接收超声信号, 16通道超声采集仪器进行数据采集, 探头布局为一发一收模式, 采集模式采用外部触发模式, 激励频率为50 kHz, 探头间距为8 cm, 采样率为5 MHz。获取厚度随时间动态变化的初始超声回波信号能量图, 如图7(a)所示。由图可知, 厚度有明显变化现象, 相应地, 规律的直达杂波干扰亦很明显。

图7 实验数据处理结果对比

根据预处理后的数据特点, 选取未燃尽介质的回波信号作为原始数据S的数据来源, 燃尽介质的回波信号作为杂波模型D0的数据来源, 利用直接自适应相减方法和结合线性Radon变换的自适应相减方法对数据进行处理, 在线性Radon变换中, 设置参数p为0.000 02, 参数x为0.005, 将信号先进行线性Radon变换映射至线性Radon域, 可得到实际实验原始信号和经过处理后的信号能量对比图, 如图7 所示。

根据能量对比图, 选取燃烧时间第1 s, 2.5 s和4 s信号数据进行处理前和处理后的波形对比, 得到如图8～图10 所示的波形对比图。由图7～图10 可知, 对实际实验数据而言, 直接对信号做自适应相减并不能去除杂波干扰, 而结合线性Radon变换的自适应相减方法能够很好地压制杂波并还原出有效波数据。通过将算法应用于实际场景的处理结果, 同样验证了结合线性Radon变换的自适应相减方法的有效性和实用性。

图8 第1 s实验数据处理结果的波形对比

图9 第2.5 s实验数据处理结果的波形对比

图10 第4 s实验数据处理结果的波形对比

4 结 论

常规处理超声混叠信号的方法主要利用信号的时频域所呈现出的差异性进行分离处理, 此类方法应用在诸如火箭发动机等大厚度介质的检测场景中时, 其采集到的信号并未表现出明显可辨的差异性特征。本文根据采集到的多条信号在时空域所呈现出的明显差异特点, 采用自适应相减方法进行分离处理, 又借助线性Radon域聚焦投影的特点, 从二维角度出发, 将信号从t-x域转换至线性Radon域, 借助信号在线性Radon域表现的差异性进行自适应相减分离处理。多次仿真实验结果表明, 结合线性Radon变换的自适应相减方法能够很好地适用于时频域差异性不显著的超声混叠信号分离场景, 且其厚度解算结果相对误差在0.65%及以下。通过在实际场景中的应用, 也充分证明了该方法能够很好地起到压制杂波干扰, 还原有效信号的作用, 本方法为大厚度介质测量获取的混叠信号的分离提供了新思路, 具有较好的应用前景。