一种抗噪声轴承故障诊断方法

陈露萌,李一鸣,黄民

(北京信息科技大学 机电工程学院,北京 100192)

0 引言

滚动轴承是数控机床和各种旋转机械系统的关键支承零部件。由于设备长期运行且工作环境恶劣,滚动轴承极易遭受结构损伤,若发生故障则会造成巨大的经济损失甚至人员伤亡[1]。实际工作环境中,滚动轴承的故障诊断往往伴随有噪声干扰。因此,研究在噪声环境中的轴承故障诊断方法具有重要意义[2]。

随着深度学习技术的飞速发展,不少学者将此技术应用于故障诊断的研究。深度学习模型中的非线性处理层能够自适应地提取原始数据中的故障特征,弥补了人工特征提取及浅层网络特征挖掘不足的缺陷。田科位等[3]将SENet结构引入到残差块中,提出了一种改进深度残差网络的轴承故障诊断方法;刘洋等[4]将注意力机制模块与一维卷积神经网络结合进行轴承故障诊断,有效提升了诊断准确率;Yan等[5]提出了一种优化的堆栈变分降噪自编码器,提升了自编码器模型的抗噪性能,并将其应用于轴承故障诊断;谢天雨等[6]提出了一种基于卷积神经网络和有效通道注意力模块的滚动轴承故障诊断方法,提升了模型在噪声条件下的特征提取能力;Jin等[7]提出的AAnNet模型由两个宽核卷积层和两个GRU层组成,并融合了注意力机制,有效提升了模型的抗噪性能,但在大负载条件下却表现不佳;许子非等[8]提出了MTSC-CNN模型,通过多尺度卷积进行特征提取,提升了模型的诊断准确率和抗噪性能;高玉才等[9]将自注意力机制引入双向长短时记忆网络,并将其应用于轴承故障诊断,有效提升了诊断模型的稳定性;赵凯辉等[10]结合Inception卷积结构的多尺度抽象特征提取能力与双向长短时记忆网络时序建模的优势,提出了基于Inception-BLSTM模型的故障诊断方法,提升了模型的抗干扰能力,诊断准确率达到99.6%。

上述方法虽取得了相对不错的故障诊断效果,但模型的深层特征提取能力和抗噪性能还需要加强,在高噪声条件下的诊断准确率和模型稳定性有待提升。由此,本文提出了一种融合可微架构搜索(differentiable architecture search,DARTS)算法[11]、卷积神经网络(convolutional neural network,CNN)和双向长短时记忆网络(bi-directional long-short term memory,BiLSTM)的DARTS-CNN-BiLSTM模型用于抗噪声的轴承故障诊断。

1 DARTS-CNN-BiLSTM故障诊断模型的建立

一维振动信号包含丰富的轴承状态信息,当受到噪声干扰时,表征故障状态的有用信息与干扰信息混叠,造成特征提取困难。为了从振动信号中提取能表征故障的深层空间特征并提升特征提取网络的抗干扰能力,本文构建了一种新的卷积神经网络并将其命名为DARTS-CNN,具体构建方式是通过堆叠5个卷积单元模块来增加网络深度,然后使用可微架构搜索算法对卷积单元模块的内部结构进行针对性寻优,从而找到最适合含噪轴承数据特征提取的优秀拓扑结构。此外,为了弥补DARTS-CNN网络无法提取振动信号时序特征的缺陷,本文在其后加入了双向长短时记忆网络来提取时序特征并进行特征融合。最后,将融合的特征输入到分类器中进行故障模式识别。本文构建的轴承故障诊断模型整体结构如图1所示,主要由DARTS-CNN网络、BiLSTM网络和分类器三部分组成,具体参数见表1。

图1 DARTS-CNN-BiLSTM模型的完整网络结构

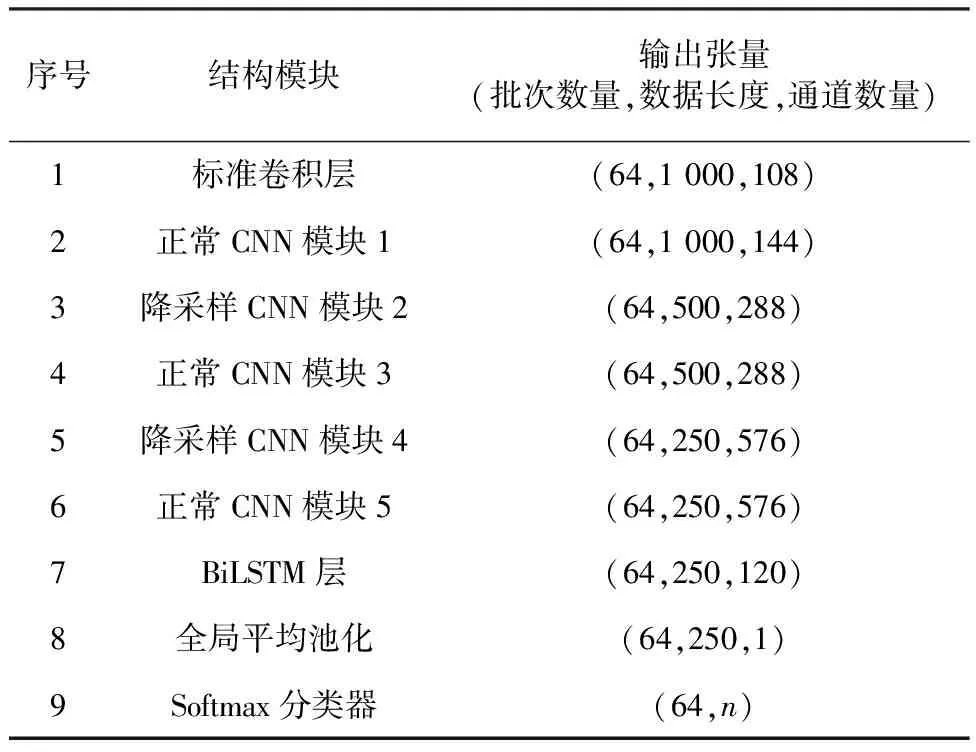
表1 DARTS-CNN-BiLSTM模型参数

1.1 DARTS-CNN网络

卷积神经网络的特征提取原理是通过卷积核实现对振动数据输入变量的动态加权融合。每个卷积核可以对局部变量进行处理,随着卷积核的移动便可提取振动信号在不同时间节点上的空间特征。因此,卷积神经网络的结构对特征提取效果至关重要。

DARTS-CNN网络先使用一个步长为1的宽核卷积(15×1)对原始一维振动信号进行初步特征提取,然后按顺序将正常卷积单元模块(normal CNN cell)和降采样卷积单元模块(reduction CNN cell)进行堆叠,这两种单元模块的内部结构均通过DARTS算法寻优得到,且同种模块的内部结构是共享的。其中,降采样单元通过将与输入节点相连的操作的步长变为2来达到降采样的目的,同时还具备限制模型通道数量的作用。两种卷积单元模块的内部都包含2个输入节点(记为Ck-2,Ck-1)、4个中间节点(记为N1,N2,N3,N4)和1个输出节点Ck(下标k代表第k个卷积单元模块)。此处,节点代表的含义是特征张量,中间节点Nj可通过式(1)计算得到。

(1)

式中:o(i,j)(·)为节点Ni和Nj之间的操作。

节点之间的候选操作设置详见表2。为使DARTS算法的搜索空间尽可能丰富,共设置了13种候选操作。并且,为了模型的轻量化考虑,标准卷积、空洞卷积和深度可分离卷积设为3种最常见的小尺寸卷积核3×1、5×1和7×1,两种池化操作的卷积核大小设为3×1。卷积和池化操作的步长设为1,空洞卷积的空洞率设为2。此外,在所有卷积和池化操作中都加入了批量归一化处理,以增强神经网络的泛化能力,卷积操作的激活函数选用计算速度更快、算法适应性更强的ReLU函数。

表2 DARTS算法中的候选操作设置

DARTS算法的搜索流程如图2所示。节点之间的每个候选操作都会被赋予一个结构参数α,用来表示该操作的重要程度。

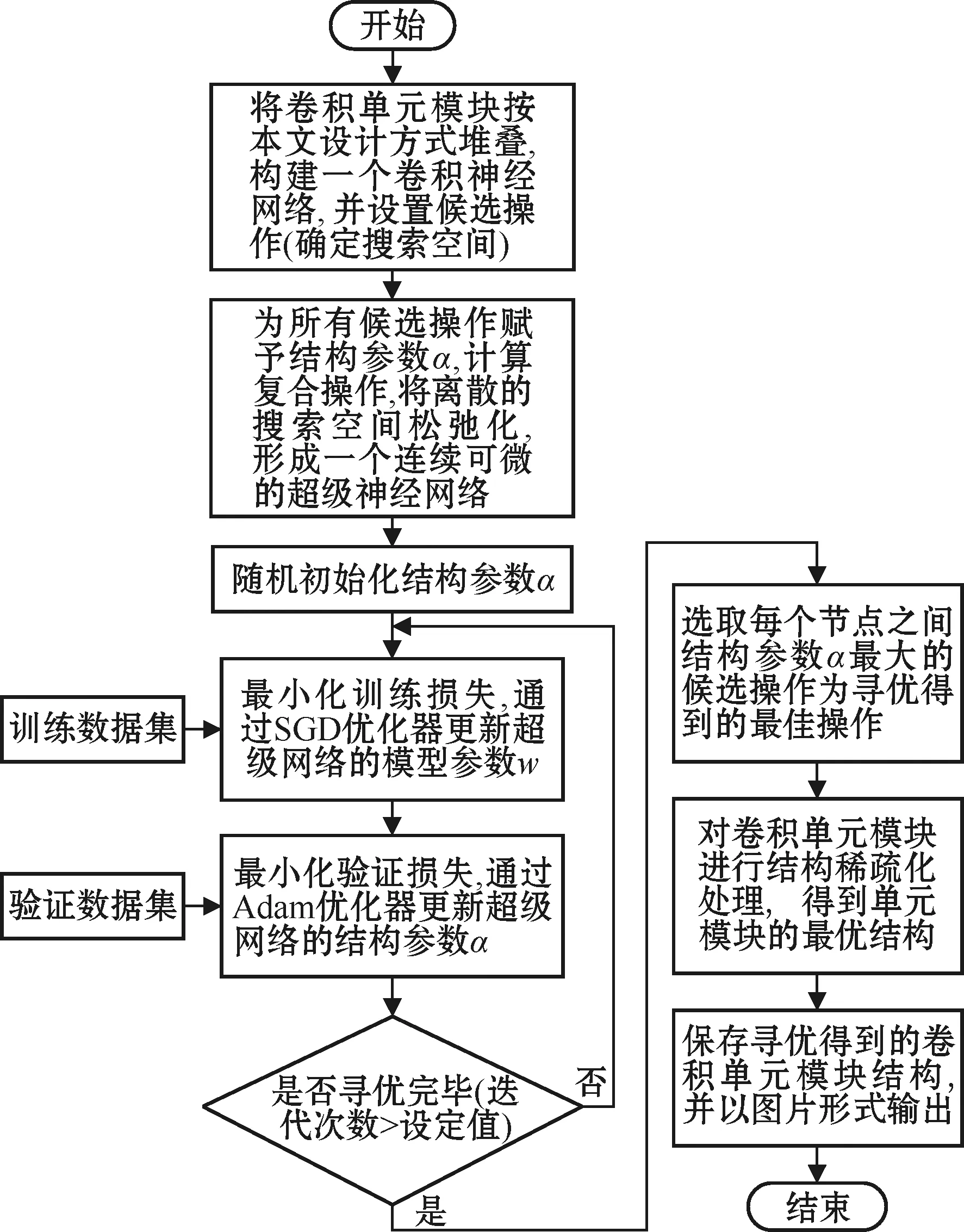
图2 DARTS算法的搜索流程

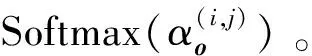
(2)

(3)

图3 超级网络中卷积单元模块的内部结构

为了找到每个节点之间的最优操作,DARTS算法通过梯度下降训练整个超级神经网络,具体的训练过程是:首先将寻优使用的数据集划分为训练集和验证集,然后通过式(4)得到最优模型参数w*,此处为了提升算法效率,优化方法采用的是元学习中常用的近似梯度计算。

(4)

最后,再通过式(5)得到最优结构参数α*。

α*=argminαLval(w*,α)

(5)

式中:Lval为验证损失。

训练结束后,通过式(6)从每个节点之间的候选操作中选出最优操作。

(6)

此外,为了使卷积单元模块的结构稀疏化,DARTS算法会对所有保留下来的最优操作的结构参数α从大到小进行排序,裁剪掉排序靠后的操作,以保证每个中间节点仅保留两个输入。

最终,本文使用西储大学轴承数据集(添加了额外随机噪声)经过50轮迭代寻优得到的卷积单元模块内部结构如图4所示,使用渥太华大学轴承数据集(添加了额外随机噪声)经过50轮迭代寻优得到的卷积单元模块内部结构如图5所示。

1.2 BiLSTM网络

卷积的运算性质决定了DARTS-CNN网络只能提取出丰富的信号空间特征,而无法提取一维振动信号中的时序特征。但是,由于卷积运算后的空间特征值是按照时间顺序排列的,因此振动信号在时间维度上的特征得以保留,即振动信号的时序特征隐含在了DARTS-CNN网络输出的空间特征值序列中。这种时序特征可以反映出滚动轴承在工作过程中的故障状态,所以,本文在DARTS-CNN网络后面加入可以从该空间特征值序列中提取出时序特征的BiLSTM网络。

BiLSTM是对LSTM[12]的改进,其结构如图6所示,该网络将DARTS-CNN输出的空间特征值序列按照时间步划分,然后将划分好的特征数据分别以时间正序排列和时间反序排列输入到两层独立的LSTM网络中,这样就可以从时间正反两个方向分别提取时序特征,再将双向时序特征通过联级操作(Concat)从通道维度进行特征融合,最后输出。相比于单层的LSTM网络,BiLSTM能够捕获更多的信号时序特征,对长信号的适应能力更好。

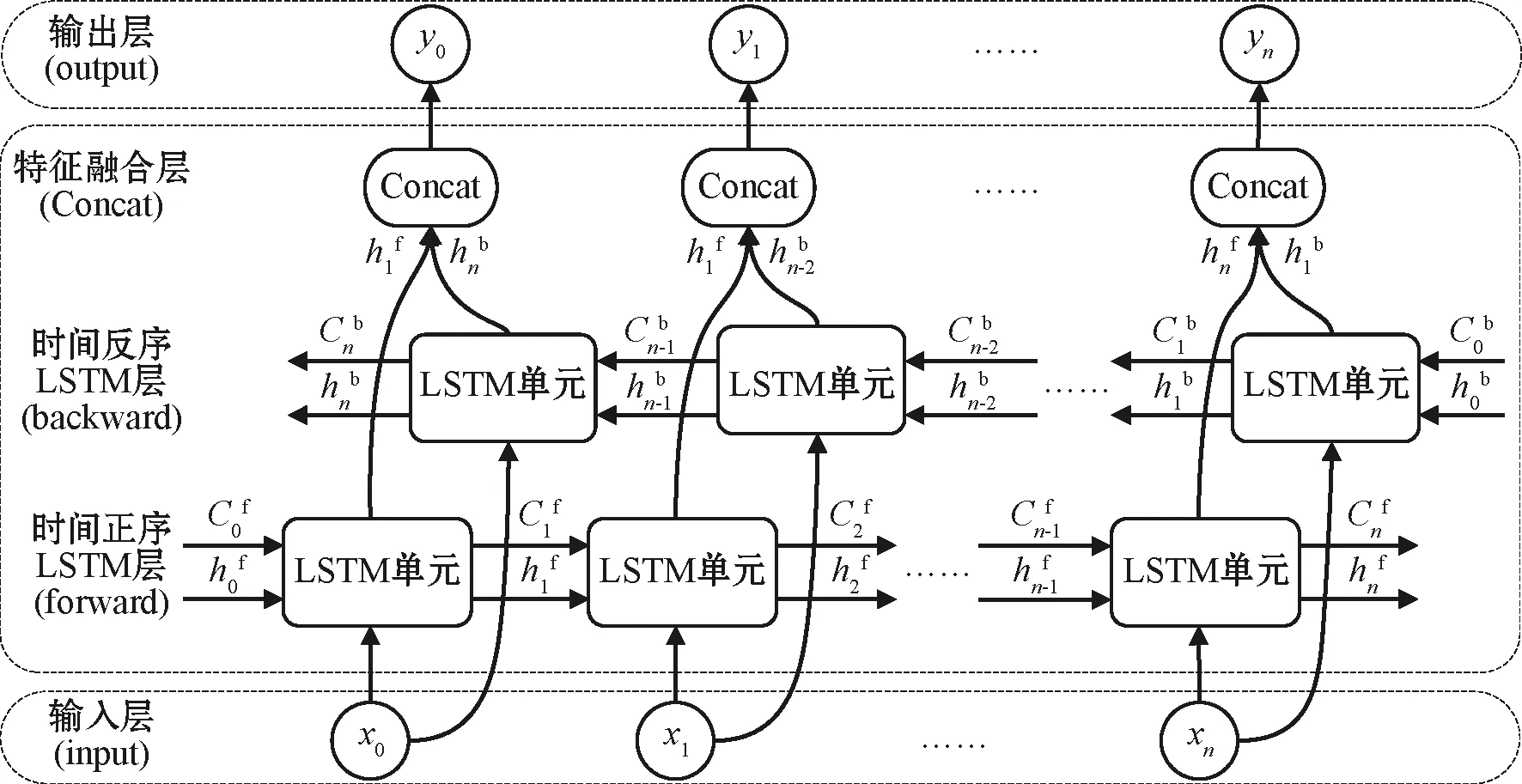
图6 BiLSTM网络结构

DARTS-CNN和BiLSTM结合能够捕捉振动信号中的空间和时间特征并将其融合,从而更加全面地反应轴承在工作过程中的故障状态,为模型分类器提供更丰富的特征矩阵,提升诊断准确率。

1.3 全局平均池化层和分类器

为减少模型参数量,本文使用全局平均池化(global average pooling,GAP)代替全连接层。全局平均池化可以精简冗余数据,改善全连接层训练速度慢、易造成模型过拟合等问题,同时还能保持空间变换的稳定性[13]。每一张特征图经过全局平均池化处理后输出一个节点,计算过程详见文献[14]。最后,通过Softmax分类器完成故障分类。

2 实验

2.1 原始数据集

为验证本文方法的有效性和先进性,分别在美国凯斯西储大学轴承数据集和加拿大渥太华大学轴承数据集上进行了故障诊断实验。

西储大学数据集使用的是SKF6205深沟球轴承,分别采集了3种负载工况下(0.746 kW、1.491 kW、2.237 kW)的轴承振动信号,采样频率为12 kHz,故障类型包括:内圈故障、外圈故障、滚珠故障和健康数据,故障损伤直径分为小尺寸(0.178 mm)、中尺寸(0.356 mm)和大尺寸(0.533 mm)。

渥太华大学数据集使用的是ER16K深沟球轴承,振动信号采样频率为200 kHz。轴承故障类型包括:健康、内圈故障、外圈故障、滚动体故障、内外圈及滚动体的复合故障。转速变化包括:先升后降(先从882 r/min升至1 518 r/min再降至1 260 r/min)、先降后升(先从1 452 r/min降至888 r/min再升至1 236 r/min)。

2.2 数据增强及样本划分

为了在保证数据时序信息不变的情况下,增加样本数量,以缓解小样本训练造成的模型学习困难,本文使用滑动窗口重叠采样对原始数据进行数据增强。

根据轴承的故障频率和采样频率,将滑动窗口长度设为1 000个数据点,重叠采样率设为30%(即滑窗步长为700)。数据增强后的样本数量可通过经验公式(7)计算得出。

(7)

式中:lnum为输入原始数据总长度;Wnum为滑动窗口长度;Snum为滑窗步长;Tnum为新样本数量(向上取整)。

数据增强后,本文将西储大学轴承数据集和渥太华大学轴承数据集都按照5:5的样本比例划分了训练集和验证集用于DARTS算法寻优。

然后,又将这两种数据集按8∶2的样本比例重新划分了训练集和测试集用于轴承故障诊断模型的完整训练和测试。根据电机负载条件的不同,本文将西储大学数据集划分为三个子集,分别命名为数据集A(电机负载为0.746 kW,电机转速为1 772 r/min)、数据集B(电机负载为1.491 kW,电机转速为1 750 r/min)、数据集C(电机负载为2.237 kW,电机转速为1 730 r/min),每个子集的训练样本数量为6 400,测试样本数量为1 600。根据转速变化的不同,本文将渥太华大学数据集划分为两个子集,分别命名为数据集D(转速先升后降)和数据集E(转速先降后升),每个子集的训练样本数量为4 000,测试样本数量为1 000。

西储大学数据集的故障分类标签对应关系如表3所示,渥太华大学数据集的故障分类标签对应关系如表4所示。

表3 西储大学轴承数据集故障分类标签对应关系

表4 渥太华大学轴承数据集故障分类标签对应关系

2.3 实验环境及参数设置

采用自主配置服务器,64位Windows10操作系统,处理器为Intel core i9 11900k CPU,128 GB运行内存,NVIDIA Geforce RTX 3090 GPU,24 GB显存,开发环境为PyTorch 1.10.0,CUDA 11.3,Python 3.8。模型的训练参数设置如下:训练批次(batch size)为64,迭代次数(epoch)为40,优化器为SGD,最小学习率 (learning rate min)为0.000 25,动量因子(momentum)为0.9,权重衰减率(weight decay)为0.000 3,损失函数为分类交叉熵损失。

2.4 实验分析

为方便区分,本文将使用西储大学数据集寻优得到的模型命名为DARTS-CNN-BiLSTM-A(即本文模型A),将使用渥太华大学数据集寻优得到的模型命名为DARTS-CNN-BiLSTM-B(即本文模型B),这两个模型的寻优过程及候选操作设置完全相同,模型差异只表现在寻优得到的卷积单元模块的内部结构不同。

2.4.1 西储大学轴承数据集的故障诊断实验

本文模型A在不同电机负载条件下的训练准确率和损失函数曲线如图7所示。

图7 本文模型在不同负载条件下的训练准确率和损失函数曲线

在训练迭代次数为11时,模型在3种负载条件下的训练数据集上准确率均达到100%,且趋于稳定。在数据集A、数据集B、数据集C上的训练损失分别由0.512降至0.020、由0.642降至0.043、由0.635降至0.034。当迭代次数到达26时,在数据集A、数据集B、数据集C上的训练损失值都降到最低并趋于稳定,分别为0.008、0.012、0.015。由此可知,本文所提出的DARTS-CNN-BiLSTM-A模型能够通过较少的训练迭代很好地完成收敛,且可以达到较高的训练准确率。

1) 本文模型在不同噪声条件下的诊断实验

添加额外噪声信号:为了验证不同噪声条件下本文模型A的诊断准确率及抗噪性能,在数据中分别额外添加了信噪比为-10 dB、-8 dB、-6 dB、-4 dB、-2 dB、0 dB、2 dB、4 dB、6 dB、8 dB、10 dB的高斯白噪声。信噪比(signal to noise ratio,SNR)RSN可根据式(8)计算得到,单位是dB。

(8)

式中:Psignal和Pnoise分别为有用信号和噪声信号的强度。

为保证实验的可靠性,每组实验分别进行了10次模型的训练和测试,取测试结果的平均诊断准确率(%)±平均绝对偏差(%)作为最终评价指标,平均诊断准确率可以反映模型的诊断精度,平均绝对偏差可以反映出模型的稳定性。最终实验结果如表5所示。可以看出,当信噪比大于等于4 dB时(低噪声),模型在3种负载工况下均能保持98%以上的高诊断准确率;当信噪比大于-4 dB小于4 dB时(中噪声),模型在3种负载工况下的平均诊断准确率虽有所下降,但仍能达到95%以上;当信噪比大于等于-6 dB小于等于-4 dB时(高噪声),模型的平均诊断准确率保持在90%以上;当信噪比为-10 dB时(严重噪声),模型在3种负载工况中的平均诊断准确率分别降低至83.51%、84.02%、83.68%。由此可知,本文所提出的DARTS-CNN-BiLSTM-A模型在不同程度的噪声干扰中仍能保持较高的诊断准确率,对中低噪声的抵抗能力非常明显,具备良好的抗噪性能,且模型准确率的平均绝对偏差较小,稳定性能好。

表5 本文模型A在不同噪声条件下的平均诊断准确率和平均绝对偏差 %

此外,为了分析该模型对每个故障类别的分类情况,本文使用多分类混淆矩阵展示了当信噪比为-4 dB时最后一次测试的结果,如图8所示。图中横坐标表示故障的真实标签,纵坐标表示故障的预测标签,主对角线上的数字代表模型对每一类别正确识别的样本数量,其余位置则是分类错误的样本数量。从图中可以看出,在数据集A上,模型对标签为0、1、2、7的故障分类完全正确,标签为3、5、9的只有极少样本被分错;在数据集B上,模型对标签为0、3、6、7的故障分类完全正确,标签为1、2、5的只有极少样本被分错;在数据集C上,模型对标签为0、3、7、9的故障分类完全正确,标签为1、2、5、6只有极少样本被分错。在3个数据集上,模型分类错误的样本主要集中出现在类别4和8中,由此可以推断,当信噪比为-4 dB时,本文模型A除了对4、8两类较易混淆,其余类别均能够高水平识别。

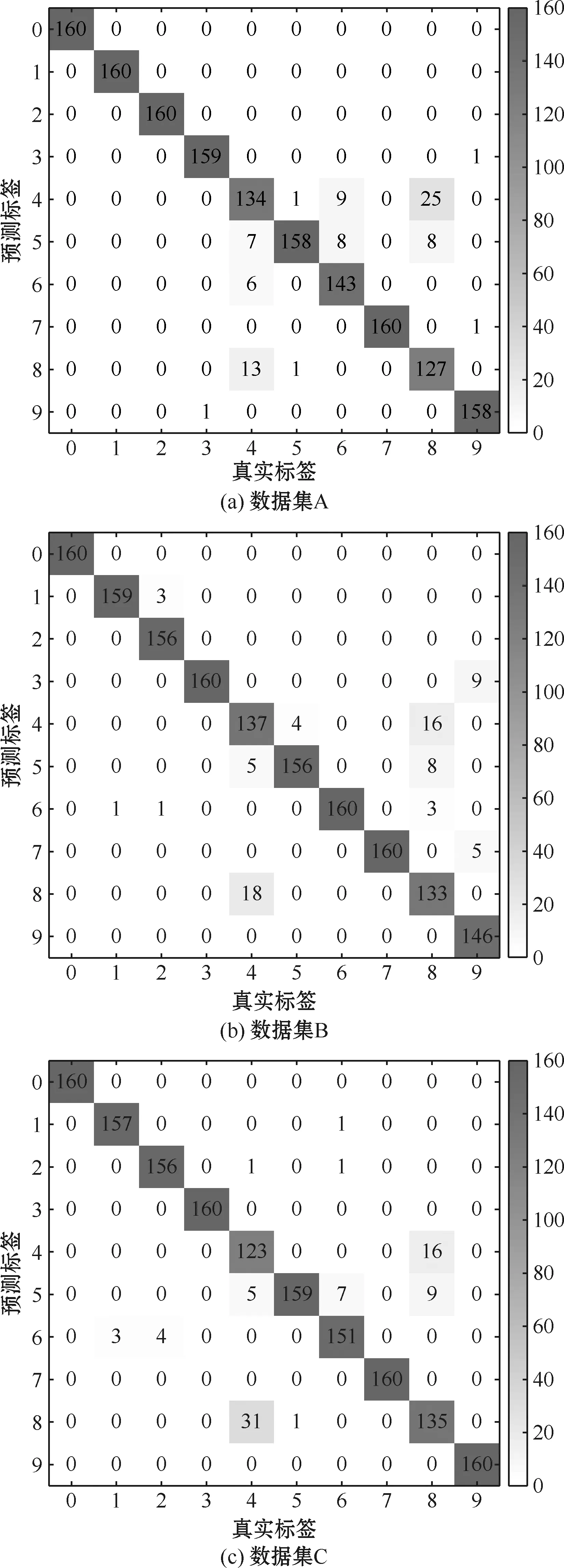
图8 本文模型A在SNR为-4 dB条件下的测试结果混淆矩阵

2) 与其他模型的性能对比实验

为验证本文模型A在诊断准确率和抗噪性能上的优势,本文选取了AAnNet[7]、MTSC-CNN[8]、BiLSTM+自注意力机制[9]、Inception-BLSTM[10]这4种先进故障诊断模型进行实验对比,实验数据使用的是最常用的0.746 kW负载工况下的轴承数据(即数据集A)。为了对比模型的抗噪性,在数据中分别添加信噪比为-10 dB、-8 dB、-6 dB、-4 dB、-2 dB、0 dB、2 dB、4 dB、6 dB、8 dB、10 dB的额外噪声。每组噪声实验中,所有模型均使用相同的数据和训练方式完成训练与测试,每个模型进行10次训练和测试,取测试结果的平均诊断准确率(%)±平均绝对偏差(%)作为评价指标。

对比结果如表6所示,AAnNet模型在信噪比大于等于0 dB的低噪声条件下能保持95%以上的诊断准确率,但在信噪比小于0 dB的中高噪声条件下,此模型的识别效果不够理想;MTSC-CNN模型与AAnNet模型的诊断效果相似,准确率略低于AAnNet,但模型稳定性更好;BiLSTM+自注意力机制模型只能在信噪比大于等于4 dB的极低噪声条件下达到较好的诊断准确率,其抗噪性能和模型稳定性是5种对比模型中表现最差的;Inception-BLSTM模型在信噪比大于等于-4 dB的低中噪声条件下均能保持90%以上的诊断准确率,且模型稳定性表现良好,但对于信噪比小于-4 dB的高噪声数据,模型诊断性能明显下降;本文提出的DARTS-CNN-BiLSTM-A模型在信噪比大于等于-6 dB的中高噪声条件下均能保持90%以上的诊断准确率,且对于信噪比大于等于-10 dB小于-6 dB的重噪声数据,本文模型仍能保持83.51%以上的诊断准确率,是所有对比模型中诊断准确率和模型稳定性表现最好的。在信噪比分别为-10 dB、-8 dB、-6 dB、-4 dB、-2 dB、0 dB、2 dB、4 dB、6 dB、8 dB、10 dB的噪声条件下,本文模型与其他模型中准确率最高的Inception-BLSTM模型相比,平均诊断准确率分别提升了8.93%、5.74%、3.54%、4.71%、3.32%、2.31%、0.55%、1.11%、0.98%、1.03%、0.19%。

表6 多种模型在不同噪声条件下的平均诊断准确率和平均绝对偏差对比 %

2.4.2 渥太华大学轴承数据集的故障诊断实验

为验证本文所提方法在更复杂工况下的轴承数据集上也具备良好的适应性,本文使用渥太华大学的变转速数据集对DARTS-CNN-BiLSTM-B模型进行了抗噪性能实验。在数据中分别添加信噪比为-8 dB、-4 dB、0 dB、4 dB、8 dB的额外噪声,选取在前述对比实验中表现较好的AAnNet[6]和Inception-BLSTM[9]作为对比。每组噪声实验中,所有对比模型均使用相同的数据和训练方式完成训练与测试,每个模型进行10次训练和测试,取测试结果的平均诊断准确率(%)±平均绝对偏差(%)作评价指标。

实验结果如表7所示,在数据集D上,AAnNet在无噪声干扰时的平均诊断准确率可达97.88%,当受到信噪比大于等于0 dB的低噪声干扰时,能保持90%以上的诊断准确率,但在信噪比小于0 dB的中高噪声区间诊断准确率下降很快,当信噪比小于等于8 dB时,平均诊断准确率已低于65%;Inception-BLSTM在信噪比大于等于-4 dB的中低噪声区间平均诊断准确率可达到90%左右及以上,当受到信噪比为-8 dB的高噪声干扰时,平均诊断准确率维持在80%左右;本文提出的DARTS-CNN-BiLSTM-B模型在无噪声干扰时的平均诊断准确率高达98.85%,当处于信噪比大于等于-4 dB的中低噪声区间时,平均诊断准确率也能保持在95%左右及以上,当信噪比为-8 dB时,平均诊断准确率仍能达到85%以上。本文模型B的抗噪性能优于其他对比模型,在信噪比分别为-8 dB、-4 dB、0 dB、4 dB、8 dB的噪声条件下,相较于其他模型中准确率最高的Inception-BLSTM模型,平均诊断准确率分别提升了5.70%、5.42%、2.65%、2.59%、1.57%。在数据集E上,本文模型B在无额外噪声干扰时的平均诊断准确率为98.38%,当信噪比大于等于-4 dB时,平均诊断准确率仍保持在94%以上,当信噪比为-8 dB时,平均诊断准确率达到85.65%。相较于其他模型中准确率最高的Inception-BLSTM模型,本文模型B在信噪比分别为-8 dB、-4 dB、0 dB、4 dB、8 dB的噪声条件下平均诊断准确率分别提升了6.45%、5.70%、2.43%、2.28%、1.52%,模型稳定性也优于其他模型。

由上述实验可知,本文所提方法在两种轴承故障诊断数据集上均表现出良好的适应性,能够达到较高水平的诊断准确率,且抗噪性能及模型稳定性均超越其他对比模型。

表7 多种模型在变转速及不同噪声条件下的平均诊断准确率和平均绝对偏差 %

3 结束语

本文针对滚动轴承在噪声环境中故障诊断准确率低、模型稳定性差的问题,提出了一种DARTS-CNN-BiLSTM抗噪声轴承故障诊断模型。以原始一维振动信号为输入,在模型设计方面提出使用可微架构搜索算法对CNN网络进行结构寻优,并将DARTS-CNN网络与BiLSTM网络结合,进一步改善了CNN无法提取信号时序特征的缺陷。

本文所提方法因为引入寻优算法,与其他模型相比,具备对不同数据集适应性更强的优点,且CNN和BiLSTM的结合能同时捕捉信号的空间和时间特征,更加全面地反应轴承故障状态,从而有效提升了诊断准确率和模型综合性能,对高噪声的抵抗能力更强,可以更好地适应实际工作场景中的诊断需求。

本文方法在进行模型结构寻优时的算法效率还有待提升,未来将在这方面做进一步优化。