非等温明渠交汇流的水力-水温特性研究
殷心盼,管光华
(武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉 430072)
0 引 言
水温是天然河流及人工明渠中的水文物理特征之一,其变化对水生生物、农田灌溉及河渠内冰情具有重要意义[1-4]。在中国,北方寒冷地区的引调水工程在冬季运行时,可能会由于气温降低而出现渠道内结冰的现象[5],甚至出现冰凌下潜从而发生冰塞、冰坝等冰期运行灾害。段文刚等[6]结合南水北调工程2011-2016年冬季观测数据提出形成稳定冰盖以维持工程安全运行的水力控制方式,但此方法将大大降低渠道冬季输水能力。而刘新鹏[7]、吴素杰等[8]学者研究证明在新疆某电站采用地下井水汇入渠道以提升水温、控制渠道冰害是一项经济安全的技术措施,其从源头上提升渠道水温、减少渠冰的形成,为缓解引调水工程冬季渠冰灾害提供一种新思路。控制渠道内冰情的关键在于对渠道水温的调控。河渠水温由气候与水文过程共同决定,影响因素包含上游来流的初始温度、与大气之间的辐射热量交换,水流的潜热等[9]。段亚飞[10]等提出能够响应气象条件实时变化的动态水温快速计算办法,戴盼伟[11]等基于南水北调中线工程建立一维水温数学模型,并对冷暖冬年气象条件下的沿线水温进行分析。此外支流的热通量汇入也将影响下游河段的水温变化过程,因而在水温计算中也不可忽略。King等[12]对北极低洼地区河流水温建模计算,结果表明支流入流热通量最高可占河流全部热通量的26%。蒋博等[13]结合原型观测和数值模拟发现澜沧江支流汇入使得干流水温降低0.8 ℃。鞠鹏飞等[14]建立平面二维水动力-温度数学模型,结合实测资料对由支流引起的汉江干流温度变化进行探讨。肖婷婷等[15]对电厂温排水汇入干流水温影响范围进行研究,评价了温排水对干流水体水生态的影响程度。上述学者的研究均基于有支流或热源汇入的天然河流水温变化过程而展开,其研究对象天然河流范围大、流量变化持续时间长,而引入离线水库温水汇入干渠范围小,对于调控时间的要求更短,但当前对于水库温水汇入干渠后的水温掺混特性及对干渠水温提升效果的相关研究成果还严重不足。
离线水库温水入渠时,干支渠交汇处及其下游渠道的水力-水温特性值得探究。干、支渠交汇后受流量掺混比、渠道交汇角等多种因素影响,水流发生相互顶托掺混,使得交汇口附近的流场、水深等水力要素发生变化,如图1所示,在交汇处将具有十分复杂的三维水流特性。茅泽育等[16]采用理论分析并结合实验数据提出交汇口上下游水深比的普遍方程,并对于不同因素的影响进行讨论。Weber等[17]通过模型实验,得到了交汇角90°的明渠交汇水流流速分布规律,并在论文中给出详细实验数据。魏文礼[18]、周舟[19]等学者利用三维仿真软件Fluent对90°明渠交汇不同汇流比对于交汇口下游水流特性的影响进行探究。毛颂平等[20]对90°交汇角的等宽明渠交汇口下游污染物扩散特性进行研究,归纳总结出下游污染物扩散规律。上述学者均对干支渠交汇模型的水力、污染物扩散等特性做过相关探究,但针对非等温水流交汇的水力-温度掺混特性的研究鲜有文章涉及。
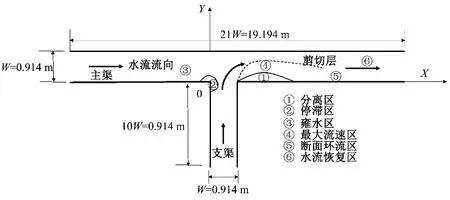
图1 干支渠交汇流态结构示意图Fig.1 Schematic diagram of the flow structure of the junction
本文以非等温的明渠交汇模型作为研究对象,借助于CFD三维仿真软件Fluent探究了不同掺混比及不同渠道交汇角条件下,交汇口下游渠道内的水力及温度掺混过程的空间分布特征,分析了非等温水流交汇后的掺混特性,获得了水温掺混均匀程度与掺混比、交汇角的定量关系。研究思路和成果可为利用离线水库温水提升干渠水温以缓解渠道冰情的相关工程提供支持与依据。
1 数学模型
1.1 控制方程
目前常用的紊流模型有雷诺应力模型(RSM)、标准k-ε紊流模型、RNG k-ε模型[21],由于本文研究明渠交汇口处水力及温度特性,水体紊动剧烈伴随漩涡产生,故选用雷诺应力模型(RSM)。该模型通过求解雷诺应力的输运方程和耗散率方程来闭合雷诺平均Navier-Stokes方程,更严格地考虑了流线曲率、涡流和应变率的快速变化的影响,对复杂流动具有更精确的模拟[22]。交汇口水流模拟满足质量守恒及动量方程,温度变化满足能量守恒方程。
(1)质量守恒方程。
(2)动量守恒方程。
(3)能量守恒方程。
式中:上标“'”代表脉动值;上标“—”代表时均值;t为时间,s;p为压强;x i,xj分别表示i,j方向的笛卡尔坐标;ui为i方向的速度,m/s;ν为运动黏性系数;为温度,℃;λ为分子热扩散系数,W/(m·℃);ρ为密度,kg/m3;Cp为水的比热,J/(kg·℃)。
雷诺应力模型RSM直接对雷诺应力输运方程进行求解,抛弃了涡黏性各向同性的假定Lander等[23-25]对方程逐项进行模化:
其中紊动涡黏性系数:
紊动能k方程:
耗散率ε方程:
参照国内外现有水温模拟研究成果,雷诺应力模型中的模型参数通常取值如表1。

表1 雷诺应力模型中的经验常数Tab.1 Empirical constants in Reynolds stress model
1.2 自由液面处理
在CFD数值模拟中,液体水与空气的交界面称之为自由液面,Fluent软件中采用体积函数法(VOF)追踪自由液面。在水气两相流中,定义函数αw和αa分别为网格单元中的水和气的体积分数。每个单元内的水、气函数满足下式:
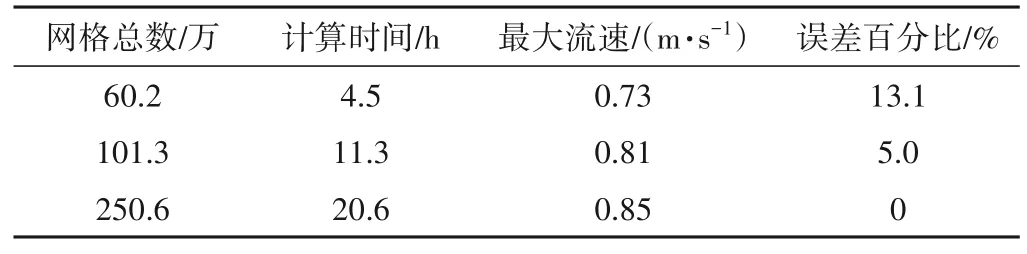
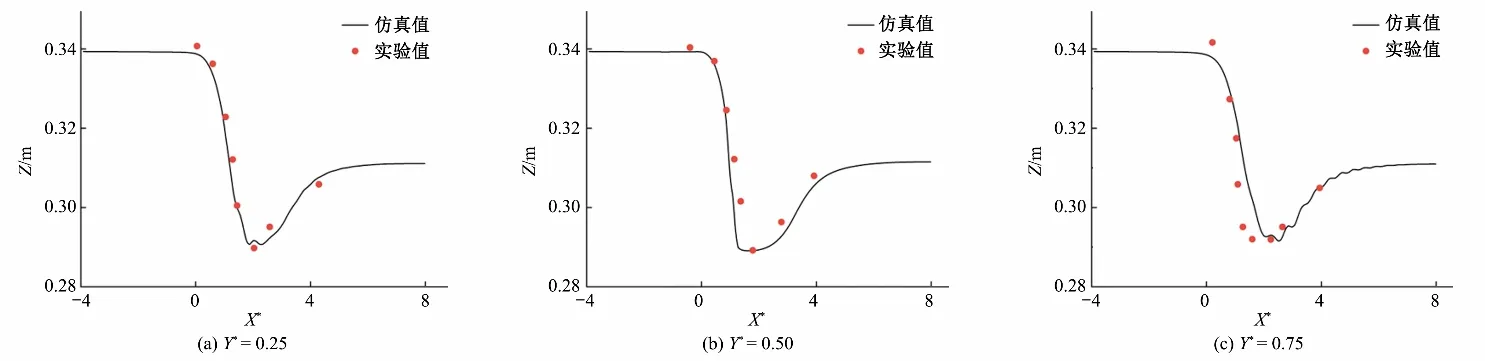
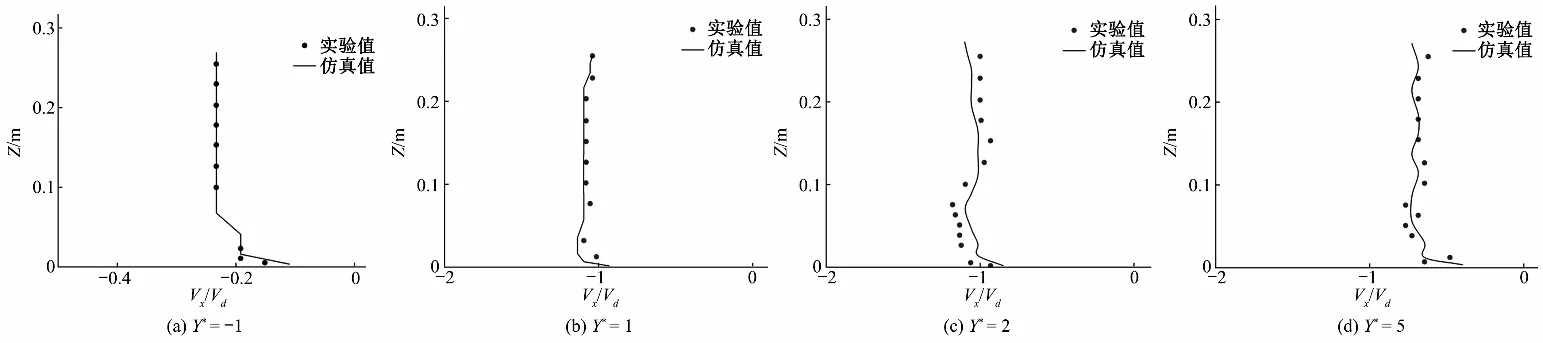
当αw=0时计算网格单元内全为气相;αa=0时计算网格单元内全为水相;0 本文研究对象为不同交汇角及不同掺混比的明渠交汇模型,建立的明渠交汇模型以Weber等[17]于2001年发表的物理实验文章中的模型为原型,该文章是明渠交汇水流相关研究领域的经典文献,提供了完整的实验数据结果,可用于本文所建立仿真模型的水动力学验证。模型交汇角为90°,如图1所示,干渠与支渠宽度均为W=0.914 m,长度分别为19.194、9.14 m。渠底部水平,模型的坐标原点为干渠交汇口下游点,X方向为水流方向,Y方向为垂直于水流方向,Z方向为水深方向。 干支渠的进水口边界条件均采用均匀速度进口,干渠入流量为Qm=0.043 m3/s,支渠入流量Qt=0.127 m3/s,交汇口下游总流量Qd=0.17 m3/s。交汇口下游出口边界采用压力出口,设定下游水位为0.31 m。干支渠的空气进口均采用压力进口,相对压强为0。水与空气接触面同样设置为压力进口,相对压强为0,以大气压为操作压力。边壁设置为无滑移的Wall边界。时态特征选择瞬态,时间步长采用自适应设置,仿真计算时间设置为300 s;最大库朗数设置为2。采用PISO算法来完成时间步长的步进;残差设置为1×10-6。在本文仿真的交汇口处水流紊动剧烈,网格区域内多为六面体网格,为获得更高的精度对湍流动能及动量离散格式采用QUICK格式,能量方程采用二阶迎风格式。 计算流体力学(CFD)本质是在划定区域内对控制方程进行离散,在各网格节点进行代数方向组的迭代求解,最后得到整个计算域的求解结果,由此可见网格划分对计算结果的准确性及精度具有重要影响。利用ICEM软件进行网格划分,仿真模型形状规则,采用正交结构化六面体网格,相较于非结构化网格,其更容易收敛。为捕捉交汇口处附近复杂流场变化,对网格进行局部加密。开展了网格无关性分析对比不同网格总数下的计算时长、计算结果的差距。以最小网格尺寸的最大流速为参照,计算其他网格尺寸下的最大流速误差百分比如表2所示。最终从计算准确性和高效性选用X方向网格尺寸为0.05 m,Y方向网格尺寸为0.05 m,Z方向网格尺寸为0.02 m,交汇口处加密网格为0.01 m的网格设置。整体网格尺寸共有节点Node 947 520 个,单元数Elements 1 012 938个,图2为网格划分示意图。网格单元质量的评判标准有很多,如歪斜度、纵横比等,该模型网格划分后最大纵横比为1.83,最小为1.03符合网格质量要求。 表2 不同网格尺寸计算结果Tab.2 Simulation results of different grid sizes 图2 网格划分示意图Fig.2 Meshing diagram 采用标准壁面函数法(Standard Wall Functions)对近壁区域模拟,忽略边壁的粗糙度影响。网格第一层节点距离壁面的无量纲距离y+的表达式为: 式中:U∞为流体流速;μ为流体的动力黏性系数;y为从边界层起始点开始沿壁面的距离。 明渠交汇口下游水流特性复杂,为验证所建立模型的准确性,将仿真结果与实验结果进行对比。为便于分析,对X、Y坐标以渠道宽度W进行无量纲化,即X*=x/W、Y*=y/W,水面线对比结果如图3所示。 图3 水面线对比图Fig.3 Comparison chart of the water surface line 由图3可见,模型计算的水面线结果与实验数据吻合度较高,在交汇口附近水面出现较大波动,这是由于在交汇口处支渠水流汇入后,干渠上游水流受阻,水面线出现壅高现象,流速变缓;在交汇口下游水面线逐渐恢复平缓,这与实际的交汇口水流特性相符,模型计算与实验结果平均相对误差为4.83%,说明模型能够准确捕捉交汇口处的水面波动。 图4为Y*=0.5处,不同横断面测线的流速分布的实验值与仿真值对比,X*=-1时,由于壅水,流速平缓,模型仿真值与实验值吻合良好。在交汇口下游处由于水流的掺混作用而出现流态剧烈紊动,仿真值与实验值在靠近渠道底部处存在一定偏差,平均相对误差为6.2%,但总体上数值模拟与实验值较为贴合,精度与准确性得以验证。 图4 流速对比图Fig.4 Comparison chart of the water velocity 干支渠交汇后下游渠道内的水力与温度特性会受掺混比例,交汇角度等多个因素的影响。在中国,北方某大型调水工程冬季运行时,渠道内会出现结冰现象,引入沿线水库的温水汇入干渠来缓解渠道冰情是一种可行的方案。根据工程资料建立实际的干支渠交汇模型,其中干渠长1 000 m,宽15 m,高3 m,支渠长500 m,宽10 m,高3 m,分别设置3种掺混比q、3种交汇角θ的工况进行仿真计算,探究交汇水流的水力及温度掺混特性。网格尺寸划分情况为X方向网格尺寸为0.5 m,Y方向网格尺寸为0.3 m,Z方向上网格尺寸为0.2 m,交汇口处网格加密尺寸为0.1 m,网格总数量约为100万。工况设置见表3。 表3 不同掺混比及交汇角工况设置Tab.3 Working conditions with different mixing ratios and junction angles 图5给出了不同掺混比工况下近水面的纵断面流速分布。结合流速云图及矢量图可以看出:随着支渠水流汇入,在交汇口上游由于水流的相互顶托作用而形成壅水,水流流速变缓;在交汇口下游处水流流态产生较大波动,干渠与支渠水流的相互掺混挤压使得流态紊乱,流线弯曲、流向偏转,靠近支渠的一端形成带有低速回流漩涡、形状上呈现上宽下窄的分离区,使得主干渠水流被压缩,过流断面被束窄,在分离区上方形成最大流速区,随着掺混距离的增加,水流逐渐趋于平顺。不同掺混比对交汇口下游流态也将产生重要影响,随着掺混比的增加,支渠流量进一步增大,主、干渠的水流掺混也更加剧烈,使得流态更为紊乱。掺混比为1∶1时,形成的分离区尺寸最大,干渠水流受到的挤压变大,导致收缩区流速进一步增大。 图5 不同掺混比纵向流速分布图Fig.5 Longitudinal flow rate distribution with different mixing ratios 图6给出了随交汇口下游距离增加,不同横断面的流速分布图。可以看到在支渠水流刚汇入干渠的X=50 m断面,由于底部流速小、近水面处流速大,渠道底部出现逆时针旋转的二次流。随着向下游距离的推移,在X=200 m断面处可以看到大漩涡分解逐渐形成两个小的漩涡,说明此时漩涡强度减弱,主、干渠的水流逐渐掺混均匀。随着掺混比的增加,支渠与干渠的流量差距减小,横断面的二次流结构也呈现出一定规律,在交汇口下游处断面涡流现象更加明显,掺混水流紊动剧烈,二次流程度进一步增强。 图6 横断面流速分布图Fig.6 Cross-sectional flow velocity distribution 3.3.1 温度掺混空间特性 在设置的工况中,干渠水温1 ℃低于支渠水温4 ℃,支渠相对高温的水汇入后将影响干渠内水温分布情况。图7分别为case1与case3掺混比分别为1∶1和1∶5且交汇角均为90°工况的水温的三维掺混空间分布特征图。由图7可看出支渠水流进入干渠后会在偏向于支渠一侧形成高温区域,并在支渠动能作用下热量逐渐扩散至对岸,温度扩散呈现出明显的三维特征。上层水体的水温扩散与中、下层横向水温扩散范围基本一致,说明支渠较高温度的水汇入干渠后在水深方向掺混较为均匀。在X<200 m时,水温的横向扩散范围随着距离的增加而逐渐扩大,而X>200 m后,水温的横向扩散基本范围基本保持不变。对比两幅图可知不同干支渠掺混比将导致支渠水流进入干渠后所形成的温度掺混特性具有明显差异,掺混比为1∶1的工况在横断面扩散呈现近似“L”形,而掺混比1∶5的工况呈现近似“D”形。 图7 不同掺混比温度掺混三维空间分布图Fig.7 3D distribution map temperature of different mixing ratios 3.3.2 温度横向扩散范围 不同支渠流量水流汇入干渠后,将导致水流之间的顶托、掺混程度不同,进而影响水温在横向的扩散范围。图8为不同掺混比在Z=1.5 m断面的水温横向扩散分布云图,颜色深浅表示水温的大小。可以看出,掺混比为1∶1的工况支渠水流汇入后在横向上扩散的范围已接近远离支渠的一侧,在交汇口下游支渠内较高温的水与干渠内的较低温的水逐渐掺混,在X=300 m之后能够看到水温的横向扩散出现较大的波动,这是由于掺混比为1∶1时,交汇口下游断面内产生强度较大的横向环流,影响着水温在横向的掺混情况。掺混比为1∶3的工况的横向掺混距离略小于掺混比为1∶1工况,这是由于此时干渠流量大于支渠流量,其流速占主导,对于支渠进入的水流具有抵冲作用,使得支渠汇入较高温度的水扩散到对岸的范围变窄。 图8 不同掺混比温度横向扩散分布图Fig.8 Transverse diffusion distribution of temperature with different mixing ratios 3.3.3 温度掺混均匀特性 支渠水流汇入干渠后,两种非等温水流逐渐混合,探究温度空间范围内的掺混均匀特性有助于了解其对干渠水温的提升效果。交汇口下游的水温受到干支渠流量、温度的影响,并随着水流向下游逐渐掺混均匀而发生变化,由前两节分析可知沿水流方向的混合水温相比水深方向更能反映支渠温水汇入后干渠内水温变化过程,故从模拟结果中提取沿程断面水温掺混平均值,图9为不同掺混比工况沿程断面平均温度变化过程线。在Fluent后处理软件中有质量加权平均(Mass-Weighted Average)和面积加权平均(Area-Weighted Average)两种求平均值的方法,本文所研究的交汇口下游流态紊乱,温度在不同断面间掺混均匀程度不一致,选用质量加权平均方式计算更为精确,表达式如下: 图9 不同掺混比横断面平均温度变化Fig.9 Average temperature change of cross section with different mixing ratios 式中:t为温度,℃;A为面积。 由图9可以看出在支渠水流刚汇入干渠时,支渠高温水与干渠低温水掺混程度最为剧烈,干渠内断面平均温度迅速上升。随着水流掺混向下游充分发展,流态逐渐趋于平顺,充分混合后断面水温逐渐降低,并且在距离支渠汇入500 m后断面水温几乎沿程不变,因此认为支渠水流汇入干渠后在500 m的距离内非等温的水流能够充分掺混。其中支渠汇入的流量越大,干渠内水温提升幅度越大,掺混比为1∶1时,干渠内水流掺混均匀后温度提升1.25 ℃,掺混比为1∶3时提升0.5 ℃,掺混比为1∶5时提升0.4 ℃。可以看出当干支渠流量相等时,支渠温水汇入对于干渠水温提升效果最为明显,温度提升值是另外两组工况的2倍。 图10为Z=1 m平面内沿程不同横向测线的水温变化曲线,横坐标表示干渠横向宽度,纵坐标为温度值。从图中可以看出,在X=50 m断面处,支渠温水汇入后在靠近支渠一侧干渠水温迅速提升,掺混比为1∶1时,干渠内靠近支渠一侧水温接近4 ℃,在横向范围内逐渐扩散,与干渠内水流进行温度掺混;在Y=8 m处出现“拐点”,此时水温开始逐渐下降,而Y=12 m处水温值为1 ℃,说明此时支渠内水温影响横向的范围仅至此处。随着支渠汇入流量的减小,掺混比为1∶3和1∶5工况,支渠水温横向扩散到对岸的范围越来越窄,分别为9 m和7 m。这是因为支渠汇入流量越大,在干渠内形成的分离区尺寸越大,干渠水流断面束窄,因此支渠温水横向扩散范围更大。在X=400 m断面处,靠近支渠侧的初始水温为低于X=50 m断面,这与图9平均水温过程线分析结果一致,由于水流的充分掺混,沿程水温逐渐降低。 图10 不同掺混比水温掺混横向变化Fig.10 Lateral change of water temperature with different mixing ratios 如表2列举的工况分别选取交汇角度θ为30°、60°、90°的矩形明渠交汇模型作为研究对象,探究不同交汇角度下明渠交汇口下游处水力与温度掺混特性。3种工况的其余参数设置均相同:干支渠的掺混比均为1∶1,干渠水温为1 ℃,支渠水温为4 ℃。由3.3节横断面沿程水温变化分析可知,在入流500 m后断面平均水温基本不发生变化,故为节约计算成本将干渠长度设定为600 m,其余参数保持不变,与第三章所述模型尺寸一致。 图11为不同交汇角度的纵断面流速分布图,可以看到不同交汇角度的支渠水流汇入后再靠近支渠形成的分离区形状和尺寸有所不同。90°交汇角工况在支渠水流汇入后所形成的分离区长度与宽度都最大,60°交汇角的分离区长度明显小于90°工况,而30°交汇角的支渠水流入汇后,在靠近支渠侧附近几乎没有出现分离区。说明随着交汇角度的减小,干渠与支渠水流的掺混剧烈程度也逐渐降低,所形成的分离区漩涡尺寸逐渐减小,交汇口下游水流能够更快恢复平稳状态。 图11 不同交汇角纵向流速分布图Fig.11 Longitudinal flow rate distribution with different angles 4.2.1 温度掺混空间特性 由4.1节分析可知不同交汇角工况下,干渠内水流流态存在差异,这将对干支渠水流的温度掺混产生影响。图12是交汇角分别为90°和30°的温度掺混三维空间分布图,两者存在明显的差异。90°交汇角工况支渠水流汇入后在干渠侧形成高温区域,在前200 m内水温在横断面的扩散近似“L”型,在200 m后沿程温度逐渐降低,说明此时干渠与支渠内的水流逐渐掺混均匀。30°交汇角工况同样在靠近支渠侧形成较高温区域,但对比90°工况,在横断面的扩散的范围和水温增加幅度都大大减小,支渠水流流入的高温区域贴近于渠道底部。随着交汇角度的减小,干渠内水流对于支渠水流的阻碍作用增大,支渠水流深入主流的横向和纵向距离都逐渐减小。 图12 不同交汇角温度掺混三维空间分布图Fig.12 3D distribution map temperature of different angles 4.2.2 温度横向扩散范围 图13为在Z=1 m处不同渠道交汇角温度横向扩散分布图,交汇角90°工况与交汇角60°在支渠刚汇入干渠时的横向扩散范围接近,而交汇角30°工况横向扩散范围则小于前两种工况。交汇角越小,支渠水流汇入干渠后在靠近支渠侧形成的分离区尺寸越小,干渠水流对于支渠水流汇入的阻碍作用越大。对比3种工况还可以发现在交汇角为90°时,在交汇口下游250 m后温度掺混出现波动,这是由于交汇口下游处存在横断面二次环流,影响了水流的温度掺混,且交汇角越大,二次环流现象越剧烈,温度掺混波动越大。 图13 不同交汇角温度横向扩散分布图Fig.13 Transverse diffusion distribution of temperature with different angles 4.2.3 温度掺混均匀特性 图14为不同交汇角沿程断面的平均温度变化曲线,同样采用第三章中提到的质量平均方法获取断面平均值。由图可知,3种交汇角工况断面平均温度的变化趋势基本一致,在支渠水流刚汇入干渠时,断面平均温度最高,随着水流逐渐掺混均匀,断面平均温度沿程逐渐下降。交汇角为90°工况温度提升值为1.25 ℃,交汇角为60°工况为1.13 ℃,差值为0.12 ℃,而交汇角为30°工况温度提升值为0.8 ℃,和90°工况差值为0.45 ℃,这是由于交汇角为30°时,支渠水流对干渠的挤压作用小于渠道交汇角为60°与90°工况,此时干渠水流占主导,因此支渠水流汇入干渠后水流扩散到对岸的距离变小,故而温度提升值也小于交汇角为90°时的水温提升值。说明渠道交汇角对于掺混后的断面平均温度具有一定影响,且交汇角越小,掺混均匀后的断面温度越小。90°工况与60°工况掺混均匀后温差较小,考虑到60°工况相较于90°工况时流态更为平顺,故在实际工程中可将干支渠交汇角设置为60°,既能满足温度掺混效果,也能减小干支渠水流交汇的剧烈紊动。 图14 不同掺混比横断面平均温度变化Fig.14 Average temperature change of cross section with different angles 图15为不同交汇角在Z=1 m平面不同横向测线上的温度沿水面宽度方向扩散的变化图。在X=50 m断面处交汇角为90°与交汇角为60°工况在靠近支渠侧的水温均接近于4 ℃,而交汇角为30°工况水温为3.1 ℃,沿着水面宽度Y方向,前两种工况的水温先保持不变后下降,而交汇角为30°工况温度先上升后下降。90°工况在横向宽度上温度掺混到Y=15 m,而60°工况水温扩散至Y=12 m,30°工况水温扩散至Y=9 m处水温即降为干渠水温1 ℃,说明随着交汇角的减小,支渠水温能够到达对岸侧的距离越来越短,影响干渠的横向范围缩窄。在X=400 m断面处,3种交汇角工况中只有交汇角为90°的工况在对岸测温度有提升,另外两个工况水温掺混仅至Y=12 m处。 图15 不同交汇角水温掺混横向变化Fig.15 Lateral change of water temperature with different angles 通过从离线调蓄水库中取用温水来调节冬季调水工程的干渠冰情,以干支渠的交汇处为研究范围进行三维建模。为分析不同因素对水力-水温掺混特性的影响,设置了3种掺混比(1∶1、1∶3、1∶5)及3种渠道交汇角(90°、60°、30°)工况进行仿真分析,得出如下结论。 (1)干支渠流量掺混比的大小对交汇口下游水力-水温掺混特性影响较大。掺混比越大,干渠水流受到挤压越大,靠近支渠侧形成的分离区尺寸越大,同时下游断面环流强度也越大。但不同掺混比工况,非等温水流均能在交汇口下游500 m范围内掺混均匀。掺混比越大,对干渠水温的改善效果越明显,在掺混比1∶1工况下,最高提升可达1.25 ℃,在实际工程中建议设置大掺混比工况。 (2)渠道交汇角大小对交汇口下游水力-水温掺混特性有一定影响。交汇角越大,支渠汇流的偏转幅度越强,导致回流分离区尺寸越大,横断面环流增强,干渠内水流紊动加剧。水流在交汇口下游充分掺混后,90°交汇角工况干渠水温提升1.25 ℃,60°交汇角工况干渠水温提升1.13 ℃,两者相差0.12 ℃,而30°交汇角工况仅提升0.8 ℃,与90度工况相差0.45 ℃。故在实际工程中,建议将渠道交汇角设置为60°,既能维持交汇口下游水流相对平顺也能保证较好的干渠温度提升效果。 本文研究成果可为大范围一维渠道冰水力建模提供依据,对于温度三维掺混过程的规律及掺混均匀距离的认识有助于在一维渠道长距离仿真中设置合理的水库温水入渠仿真边界。2 模型构建与验证
2.1 模型建立
2.2 边界条件
2.3 网格划分

2.4 水动力学验证
3 不同掺混比水力与温度掺混特性
3.1 工况设置
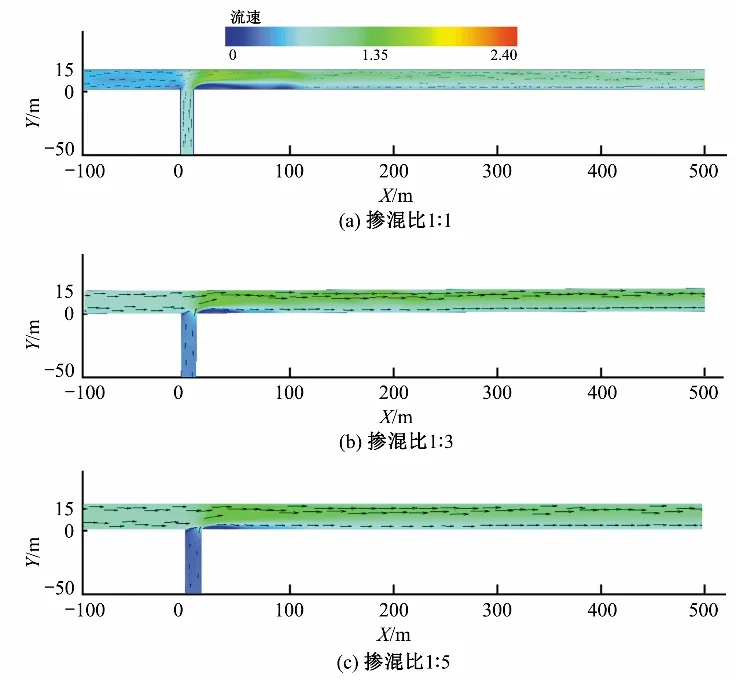
3.2 纵横断面水力特性
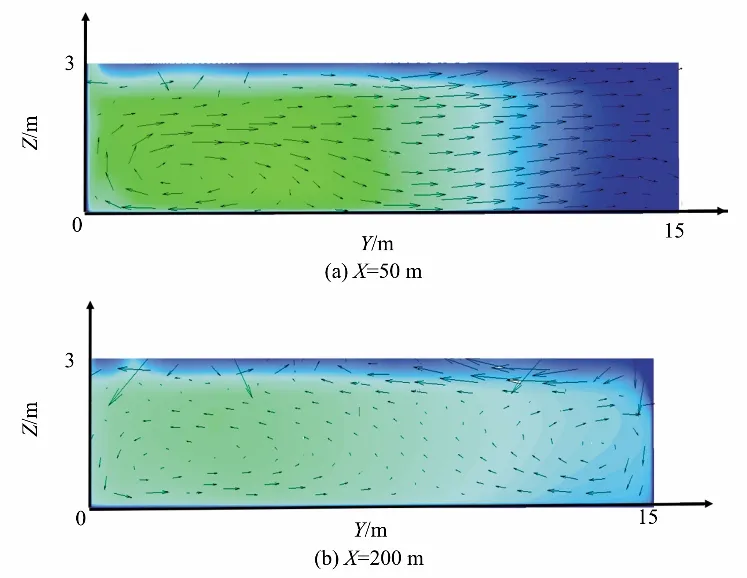
3.3 温度掺混特性分析
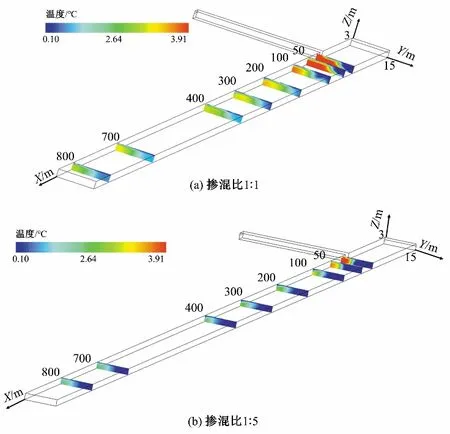
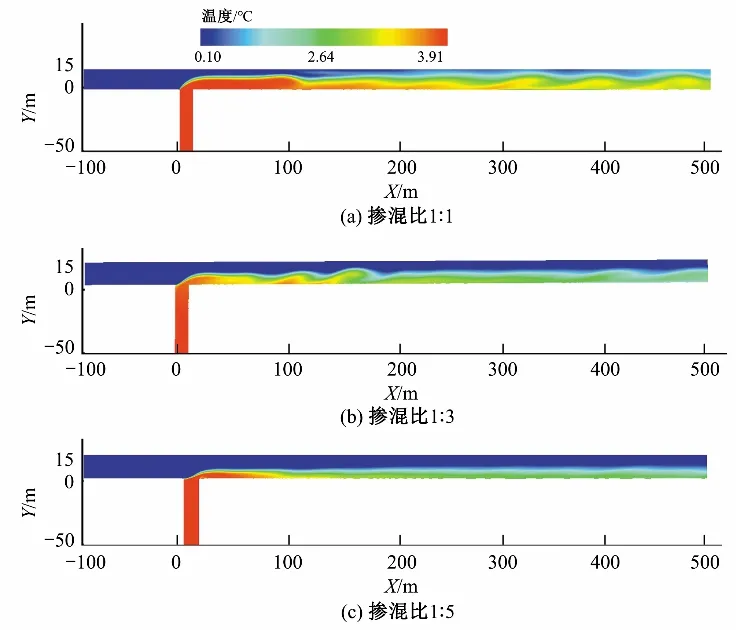
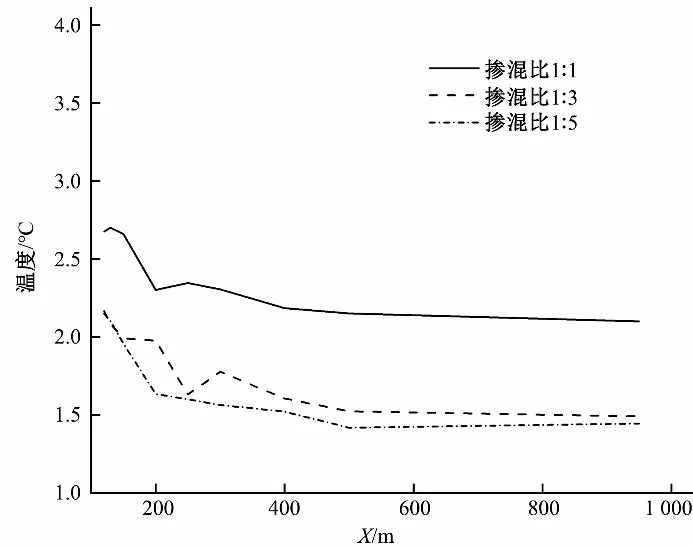

4 不同交汇角水力与温度掺混特性
4.1 纵断面水力特性

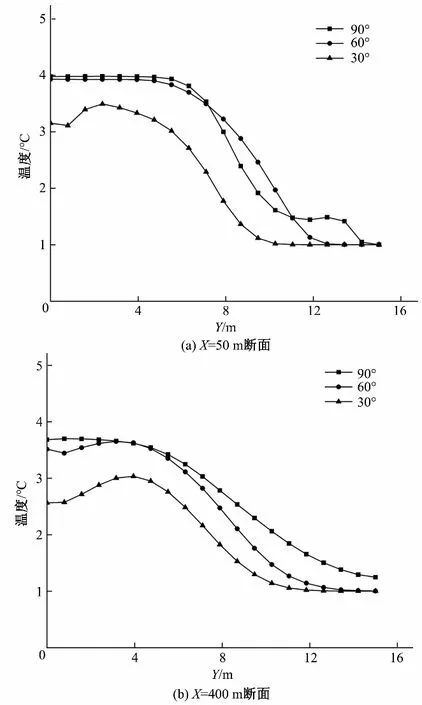
4.2 温度掺混特性
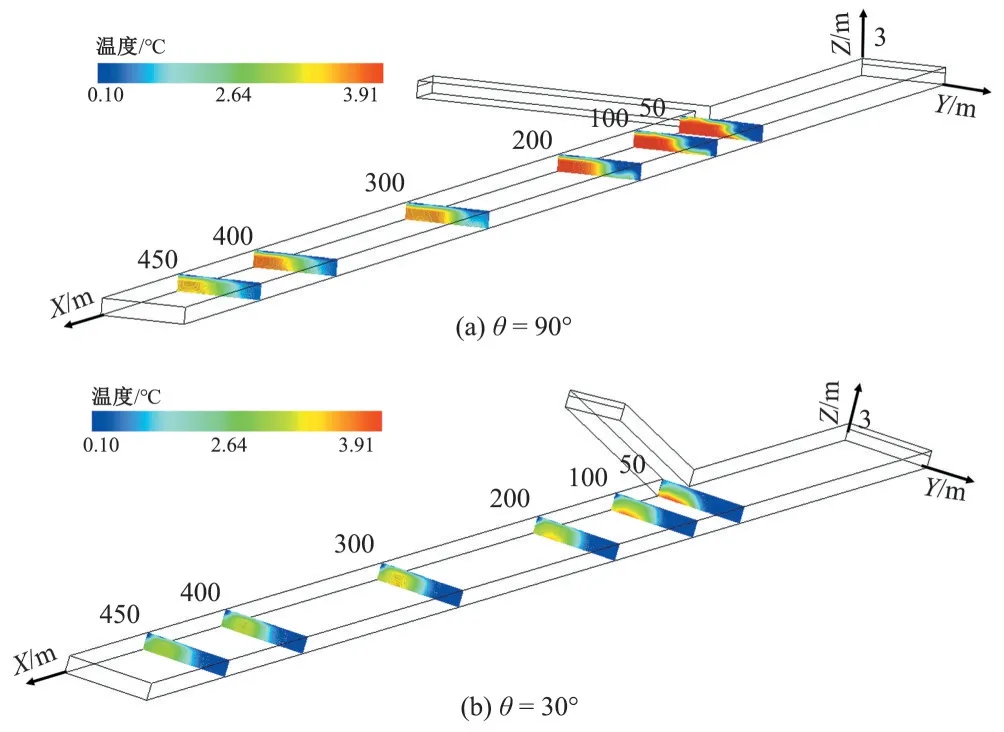
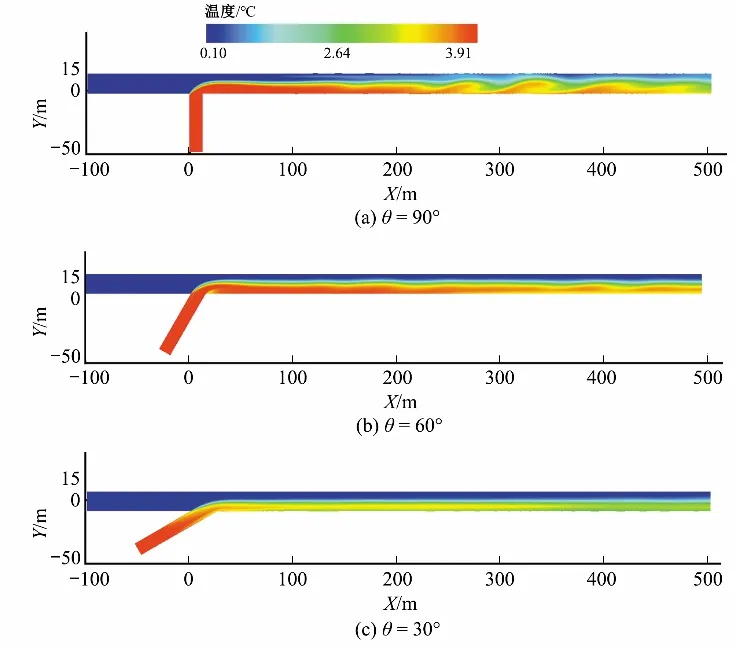

5 结 论

