基于线性单轨模型的扩展模型分析轮胎导入特性对操稳性能的影响

摘要：在常用的两轴汽车线性单轨车辆动力学模型基础上做了进一步扩展工作，引入轮胎导入特性，建立了基于线性单轨模型的扩展模型，并从理论上对轮胎导入特性与操纵稳定性的关系进行了分析。

关键词：车辆动力学；操纵稳定性；轮胎

中图分类号：U467  收稿日期：2023-03-25

DOI：10.19999/j.cnki.1004-0226.2023.05.016

1 前言

两轴汽车线性单轨模型是最简单的车辆动力学模型，将两轴汽车的实际模型简化为忽略质心距离地面高度的线性系统，可以充分解释汽车前后轴侧偏刚度、轴荷分配这些固有属性，与动态表现出的不足转向、（阶跃）横摆峰值响应时间、横摆固有频率等操纵稳定性指标的关联［1］。

然而也由于模型进行了简化，车辆的许多其他固有特性，如质心高度、悬架侧倾转向特性等与操稳性能指标的关联，无法基于该模型进行分析［2］。

当轮胎侧偏角随时间变化时，其侧向力变化并不会立即跟随侧偏角变化，而是存在一定程度的滞后，这一轮胎本身的瞬态响应特性称为轮胎的导入特性，该特性与轮胎的侧偏刚度和侧向刚度强相关［3］。由于轮胎的导入过程相比车辆的瞬态响应过程短得多，因此线性单轨模型往往忽略该过程，即假设轮胎侧向力对侧偏角的响应是即时的，不存在滞后。在这一假设下，对于轮胎而言，模型只引入其侧偏刚度特性，而不考虑侧向刚度特性。

不同厂家、规格和配方的轮胎，侧偏刚度和侧向刚度都可能有较大差异。考虑到分析轮胎侧向刚度差异对操稳性能的影响，本文基于一般线性单轨模型做了扩展，引入轮胎导入特性，从理论上分析轮胎导入特性与操纵稳定性的关系。

2 模型建立

本文采用的车辆动力学名词定义和坐标系采用SAE标准。

2.1 轮胎导入特性

3 模型分析

尽管只是将轮胎导入特性的简单一阶模型引入线性单轨模型，但引入后，整车模型的阶数由二阶增加到六阶，复杂程度大大增加，需要借助计算机工具做进一步理论分析。

3.1 导入时间

在式（5）中可以看到表达式[-Ckv]常常出现。可将该式提取出来，定义为轮胎导入时间[tr=-Ckv]。导入时间是表征轮胎导入时响应速度的重要参数，反映对轮胎输入阶跃侧偏角后，侧向力增长至稳态值的63%所用的时间。从表达式可知，轮胎侧向刚度相对其侧偏刚度越大，或车速越高，导入时间就越短，轮胎导入的响应就越快。

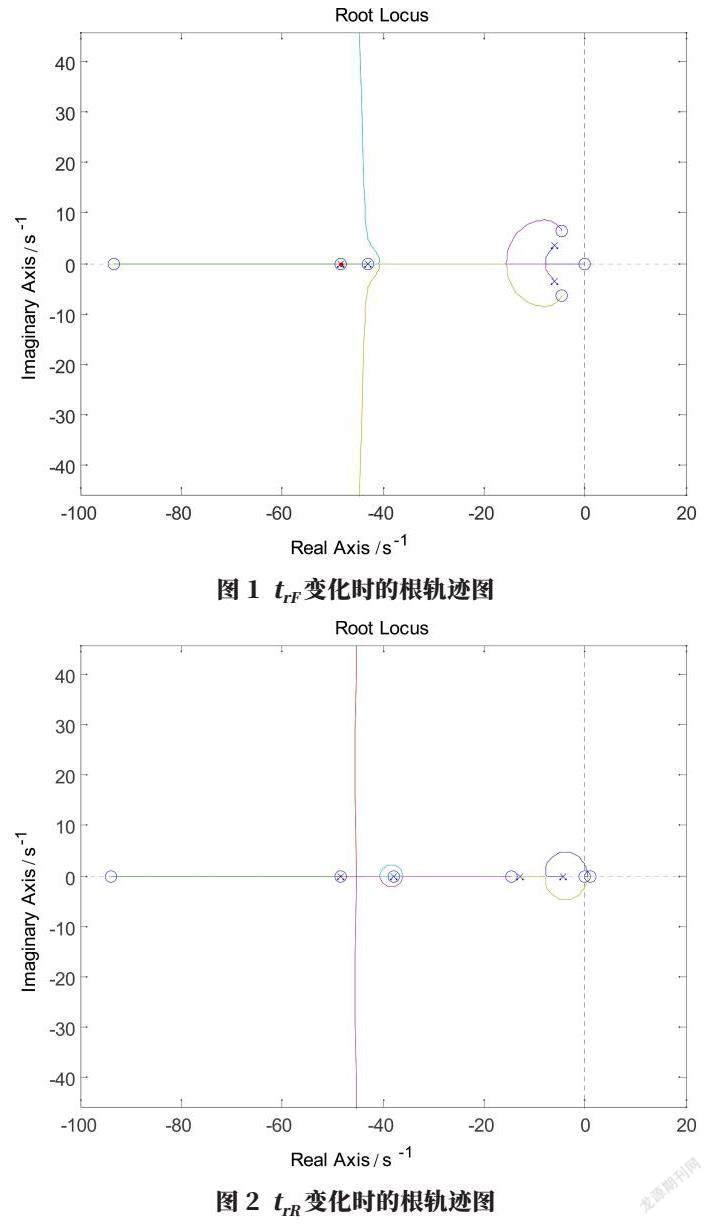
分别提取式（7）中含trF和trR的多项式，根据多项式以及给定的模型参数，可获取模型特征跟随trF或trR变化的根轨迹图。由于多项式较复杂，该操作通过计算机工具辅助完成。

图1、图2分别是在根据较能体现乘用车通常性能的某一模型参数设置下，通过MATLAB软件获取的模型根轨迹随trF和trR的变化。

由上可以看到，对于前轴，随着轮胎导入时间的增大，所有特征根实部始终还保持为负值，系统一直保持稳定；而对于后轴，随着轮胎导入时间持续增大，特征根主值可能穿过实轴变为负值，系统开始不稳定。

因此从稳定性的角度考虑，不希望后轴轮胎侧向刚度（相对其侧偏刚度）过小，具有较长的导入时间。

3.3 时域响应分析

基于与上文相同的模型参数设置，调整不同的kF和kR值，用MATLAB软件做0.4 g角阶跃转向时域分析，结果见图3～图4所示。

综上所知，总体侧向刚度越高，或者侧向刚度越多倾向分配给后轴，车辆响应越趋向于收敛，不超调。

4 结语

本文在常用的两轴汽车线性单轨车辆动力学模型基礎上，进一步扩展，引入轮胎导入特性，并根据该模型，从理论上对轮胎导入特性与操纵稳定性的关系做了简单分析。

参考文献：

［1］Manfred M，Henning W.汽车动力学［M］.陈荫三，余强等 译北京：清华大学出版社，2009.

［2］Vittore C.Motorcycle Dynamics［M］.Lulu.com，2006

［3］.William J.Palm III.System Dynamics［M］.Mc Gpraw Hill，2019

作者简介：

吕近添，男，1995年生，助理工程师，研究方向为车辆动力学。