权重和数据影响下水资源承载力评价不确定性研究
李占玲 王佳雯 叶瀛韬 董俊巧 刘星才


李占玲,
女,副教授,博士,硕士研究生导师,主要从事流域水循环模拟、水文统计、极端气候、不确定性、水资源评价等方面的研究工作。主持和参与国家自然科学基金青年基金及面上基金、北京市青年英才、中央高校基本科研业务费、 企业合作等科研项目10余项。主编教材《水资源评价与开发利用》1部,参编学术专著3部,在Journal of Hydrology,Hydrological Processes,Science of the Total Environment,《地理研究》《干旱区地理》等中英文期刊发表学术论文30余篇。先后获得北京市教育教学成果奖、第七届全国水利类专业青年教师讲课竞赛奖、北京市大学生节能节水低碳减排社会实践与科技竞赛优秀指导教师奖、中国地质大学(北京)校级教学成果奖等。
摘要:
水资源承载力是实现“空间均衡”的重要刚性约束条件,其科学评价对于地区生态文明建设与可持续发展具有重要理论与实践意义。以往研究多集中于确定性评价,然而受多种因素的影响,水资源承载力评价也存在一定的不确定性。以新疆地区为例,采用Bootstrap、均匀分布假设法的随机抽样以及随机误差生成等方法,借助隶属度及不确定度的概念,量化指标权重及指标数据不确定性对研究区水资源承载力评价结果的影响。结果表明:基于Bootstrap和均匀分布假设法,由指标权重不确定性导致的新疆地区水资源承载力评价等级不确定度分别为21%和17%,由数据不确定性导致的不确定度为8%;随着指标权重和数据不确定性的增加,研究区水资源承载力评价等级的不确定度均随之增加;通过增加等幅误差的方法表明,数据不确定性对研究区水资源承载力评价等级的影响更大。研究成果可为科学评价水资源承载力、降低其不确性提供参考。
关 键 词:
水资源承载力; 不确定性; 权重; 隶属度; 不确定度; Bootstrap
中图法分类号: TV213.4
文献标志码: A
DOI:10.16232/j.cnki.1001-4179.2023.05.007
0 引 言
水资源承载力评价是水资源科学领域的一个重要问题。20世纪90年代初,水资源承载力脱胎于资源承载力的研究,作为一个全新的概念出现于水资源的相关研究中[1-2];21世纪初,有关水资源承载力的概念、研究方法受到极大关注,并趋于完善[1];2014年左右,随着“绿水青山就是金山银山”等绿色发展理念的确立,最严格水资源管理制度的出台,水资源承载力的研究进入了新的阶段。在水资源供需矛盾突出但同时经济又面临快速增长的今天,水资源承载力问题越来越受到学者的广泛关注[3-8]。尤其是新时代“十六字”治水思路提出以来,以水而定、量水而行,水资源已成为实现“空间均衡”的重要刚性约束条件。因此,水资源承载力的科学评价对于地区生态文明建设与可持续发展具有重要的理论与实践意义。
水资源承载力评价的一般思路是,首先根据水资源承载力的内涵选用一系列评价指标,建立水资源承载力评价指标体系,然后根据各种主客观方法确定各项指标的权重,最后参考相关文献确定水资源承载力评分标准及评价等级,采用适当的评价方法或模型对某地水资源的承载力进行评价。
其中,指标权重的确定是水资源承载力评价工作中的重要内容。在現有研究中,大量文献对于指标权重的确定都非常关注,提出了很多指标权重的确定方法,例如层次分析法、遗传或改进的层次分析法[3-4]、主成分分析法[5]、因子分析法[6]、熵权法[7,9]、变异系数法、CRITIC法[10]、投影寻踪法[11]、EFAST方法[12]等。这些方法有些是对信息进行浓缩进而确定权重,有些是利用数据携带的信息量大小进行权重计算,也有些是利用数据之间波动性的大小或数据之间的相关关系大小来计算权重。杨海燕等[10]在建立涵盖水资源、社会、经济和水环境4个准则层的评价指标体系基础上,运用CRITIC-GR-TOPSIS法,对2003~2018年烟台市水资源承载力进行了评价;金菊良等[11]针对由主观定权方法导致的水资源承载力评价结果不确定性问题,提出投影寻踪(PP)方法以优化层次分析法(AHP)确定的指标权重,构建了基于PP-AHP方法定权的水资源承载力评价模型,并以安徽省水资源承载力评价为例进行了验证;王富强等[12]将EFAST方法与云理论相耦合,提出了EFAST-云模型的区域水资源承载力评价方法。基于不同方法确定的指标权重值不尽相同,很多文献均指出,权重值的差异将导致评价结果存在一定的不确定性[6,8,10-12]。然而,却鲜有研究对这种不确定性的大小进行定量化讨论。
同时,在评价指标确定后,还需要查阅大量资料获取与评价指标有关的数据信息。由于不同文献、不同数据来源或者不同统计口径等原因,同一类数据可能会存在差异,甚至相差较大。本文收集了多年《新疆水资源公报》《新疆统计年鉴》《中国环境统计年鉴》资料,发现不同来源数据间的差异有所不同:2017年新疆生活用水量数据差异达5%,2009年人均GDP数据差异达10%;工业废水排放量数据差异更大,2009~2018年每年差异均达40%以上。可见,数据之间的差异较为显著,而数据存在着的不确定性对评价结果的影响程度有多大,相关研究较少。另外,数据和指标权重二者之间对于水资源承载力评价结果的影响哪个更显著,也少有研究进行讨论。
新疆地处亚欧大陆腹地,由于气候干旱少雨且蒸发较大,长期以来面临着严峻的水资源短缺和生态环境脆弱性问题,严重制约了当地水资源与社会经济的可持续发展。2015年国家发改委、外交部、商务部联合发布了《推动共建丝绸之路经济带和21世纪海上丝绸之路的愿景与行动》,提出发挥新疆独特的区位优势和向西开放重要窗口作用,打造丝绸之路经济带核心区。水资源正是核心区经济发展的生命线。因此,研究新疆水资源能够承载的社会经济发展模式已成为丝绸之路经济带核心区建设中亟待解决的问题。开展新疆地区水资源承载力评价对于区域经济发展以及水资源可持续开发利用具有重要意义。
针对以上问题,本文以新疆地区为例,通过Bootstrap、满足特定约束条件的随机抽样、随机误差生成等方法,从评价指标权重和指标数据两个方面讨论其对水资源承载力评价结果的影响,为量化承载力评价过程中的不确定性、科学评价水资源承载力提供参考。
1 研究区与数据来源
新疆位于中国内陆,远离海洋,属于典型的温带大陆性干旱气候,降水稀少、蒸发量大,多年平均降水量170 mm。区内共有河流3 355条,其中年径流量超过100亿m3的有3条。冰川储量约21 300亿m3,占全国的42.7%,有“固体水库”之称。多年平均水资源量834亿m3,约为全国的3%。新疆区位通道独特,是中国向西开放的重要门户和丝绸之路经济带核心区。近年来该地区经济发展迅速,2021年地区生产总值接近16 000亿元,是2012年的2.16倍;全体居民人均可支配收入从2012年的12 151元增加到2021年的26 075元。
为深入分析新疆地区水资源承载能力,统筹考虑区域发展与水资源的协调状况,从2008~2019年的《新疆统计年鉴》《新疆水资源公报》《中国环境统计年鉴》等资料中收集该地区水资源承载力评价指标数据,构建水资源承载力评价指标体系和综合评价模型。
2 評价指标体系的构建
当前水资源承载力评价研究多从社会、经济、生态环境、水资源4个系统出发[13-14],或从水量、水质、水域和水流状态4个维度出发[12,15-17],筛选出重要的评价指标,进而构建评价指标体系。本文主要基于水资源、社会、经济、生态环境4个系统提出水资源承载力评价指标体系。通过综合分析水资源承载力的影响因素,参照全国水资源供需分析中的指标体系和一些关于水资源评价指标体系的研究成果,充分考虑新疆地区水资源、社会、经济及生态环境系统特征等条件,筛选了各系统反映区域水资源承载力的评价指标,如表1所列。
3 研究方法
3.1 TOPSIS评价模型
采用TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)评价模型对研究区水资源承载力进行评价。TOPSIS法属于多目标决策的综合评价方法之一,概念简单、计算过程清晰、可操作性强。该方法自1981年首次提出以来,已广泛应用于经济、交通运输等领域,目前,在水资源承载力评价、水环境质量评价、干旱评价等方面也得到了广泛应用[18-20]。其基本思路是依据评价指标与最优理想方案的接近程度,对所有选取的评价指标整体排序进而确定方案的相对优劣。基于TOPSIS评价模型进行水资源承载力评价的具体步骤可见参考文献[9,18],以模型中的贴近度来表示水资源承载力评价指数,该指数处于(0,1)之间,越接近于1,则表明承载力水平越高,评价等级标准[21]如表2所列。
3.2 指标权重的确定
由于不同方法思想和原理有所不同,因此所得的权重也有所差异。本文采用因子分析法、主成分分析法、熵权法、CRITIC权重法、变异系数法等5种方法确定指标权重,得到各指标权重的初始值及取值区间。
3.3 指标权重样本的生成
为探讨权重不确定性对水资源承载力评价结果的影响,通过两类方法生成指标权重样本:① 第一类方法是在一定范围内随机生成指标权重样本;② 第二类方法是在权重初始值的基础上增加随机误差的形式生成指标权重样本。
第一类方法具体又包括两种形式,以第x个指标为例,以5种方法得到的权重初始值作为原始样本集:① 借助Bootstrap抽样方法,在其原始样本集中随机取样,从而生成一系列新的样本;② 生成一系列满足特定约束条件的随机权重,从而生成新的权重样本集,约束条件即假设该指标服从区间[a,b]上的均匀分布,a、b分别为该指标原始样本集中的最小值和最大值。第二类方法是在权重初始值基础上分别增加≤±5%,≤±10%,≤±15%,…,≤±100%的随机误差,使用这类方法的目的是便于比较指标数据对评价结果的影响。每种方法每个指标分别取样5 000次,另外,为保证所有指标的权重加和为1,要对各指标新的权重进行归一化处理。
3.4 指标数据样本的生成
为讨论数据不确定性对水资源承载力评价结果的影响,通过在原始数据的基础上增加满足一定约束条件的随机误差项来描述数据的不确定性,从而生成一系列新的数据样本,即带有一定误差项的样本,然后针对新样本数据进行水资源承载力评价。约束条件分为两类:① 根据收集数据的实际情况,确定误差项的变化幅度;② 增加等幅误差,即在原始数据上分别增加≤±5%,≤±10%,≤±15%,…,≤±100%的随机误差。根据上述方法分别生成5 000组数据样本。
3.5 隶属度和不确定度
4 结果与分析
4.1 研究区水资源承载力评价
以《新疆水资源公报》的数据为基准(如果数据缺失,则采用《新疆统计年鉴》的数据或相关公式计算得到),基于TOPSIS评价模型对新疆水资源承载力进行评价。熵权TOPSIS模型的评价结果如表3所列。可以看出,2008~2019年新疆水资源承载力整体呈波动上升趋势,即承载力有向好的趋势。2008~2015年水资源处于超载状态,从2016年开始,水资源由超载状态转变为临界状态,水资源承载力适中,2018~2019年水资源呈弱承载状态,承载力指数良好,进一步开发利用的潜力较大。
近年来,新疆地区在践行绿色发展理念、推进节能减排降碳工作等方面取得了明显成效。根据《新疆水资源公报》数据,2016年新疆人均综合用水量较2008~2015年降低了6%,2019年又较2008~2015年降低了12%;2021年新疆公共机构人均用水量比2012年下降了25%。在建设节水型企业、推广先进节水技术产品装备等方面也做了大量工作,很多指标呈现明显下降趋势,如万元GDP用水量、万元工业增加值用水量、工业用水率、工业废水排放量,2016年上述指标较2010年分别降低43%,16%,1%,37%;2019年各指标较2010年分别降低128%,74%,1%,67%。同时,2008~2019年新疆地区水资源供水情况整体呈增加趋势。这些指标的变化均会促进水资源承载力呈现出向好的变化趋势。另外,2016年1月1日起,新疆实行了新的水资源费征收标准,这也为当地水资源承载力的提升做出了积极贡献。
4.2 指标权重对水资源承载力评价结果的影响
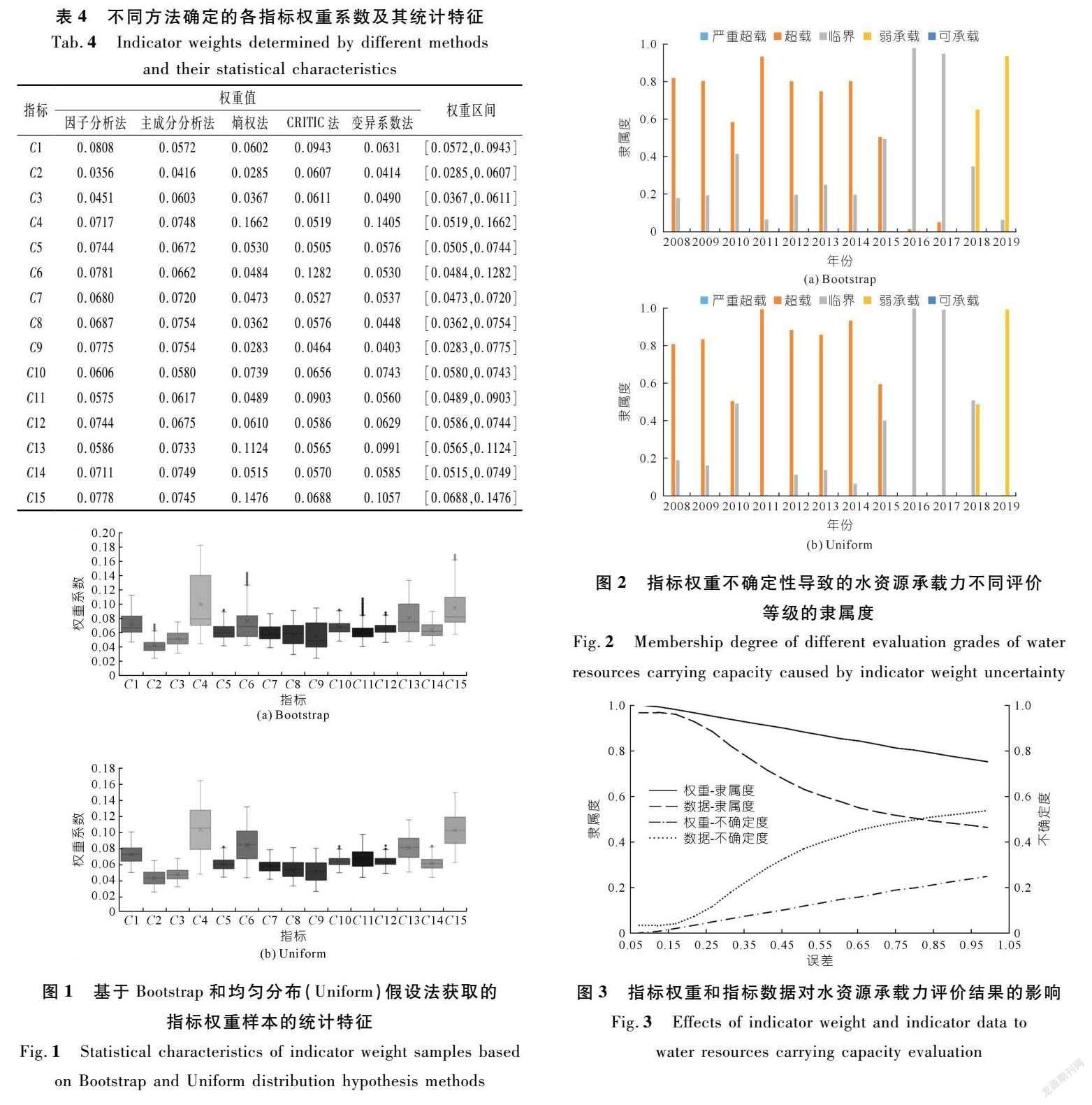
通过5种方法确定的指标权重及权重区间如表4所列。通过Bootstrap方法以及满足约束条件均匀分布假设法获取各指标权重样本如图1所示;然后再基于TOPSIS评价模型对研究区水资源承载力进行评价;将5 000组评价结果进行统计分析,计算不同评价等级的隶属度;图2给出了由指标权重不确定性导致的研究区不同评价等级的隶属度。
以Bootstrap方法为例,由图2可知,由于指标权重不确定性的影响,2008~2015年研究区水资源承载力评价等级为“超载”的隶属度为50%~93%,均值为75%,2016~2017年评价等级为“临界”的隶属度为95%~98%,2018~2019年评价等级为“弱承载”的隶属度为65%~94%,多年平均隶属度为79%;与基准结果比较(见表3),由指标权重不确定性导致的研究区水资源承载力评价等级的不确定度为21%。同样,基于均匀分布假设法的结果可知,多年平均隶属度为83%,即由指标权重不确定性导致的研究区水资源承载力评价等级的不确定度为17%。
通过在指标权重初始值上增加随机误差这一方法得到的评价结果如图3所示。可以看出,随着随机误差绝对值的增加,多年平均隶属度呈下降趋势。当随机误差绝对值由10%增加至50%时,多年平均隶属度由99%下降到88%,不确定度由不足1%上升到12%;当随机误差增加一倍(100%)时,不确定度上升到25%。
4.3 指标数据对水资源承载力评价结果的影响
不同指标原始数据的误差会传递给各个指标值。通过增加满足一定约束条件的随机误差项得到新的指标样本数据,随机误差项包括实际误差及等幅误差。实际误差是以收集到的数据实际情况为基础给定误差项的比例,假设C8、C9指标存在±10%以内的误差,C14指标存在±80%以内的误差,C15指标存在±50%以内的误差,其余指标存在±5%以内的误差,根据以上比例对每项指标的数值随机增加误差项。
当基于实际误差生成随机误差项时,2008~2015年研究区水资源承载力评价等级为“超载”的隶属度均值为92%,2016~2017年評价等级为“临界”的隶属度均值为100%,2018~2019年评价等级为“弱承载”的隶属度均值为83%,多年平均隶属度为92%(见图4)。由此可得,由指标数据不确定性导致的该地区水资源承载力评价等级的不确定度为8%。
为了与指标权重的影响进行横向比较,进一步讨论了基于原始数据增加等幅误差后的结果,如图3所示。随着随机误差绝对值的增加,多年平均隶属度呈下降趋势,尤其是当随机误差绝对值大于20%以后,多年平均隶属度下降幅度更为明显,不确定度明显上升。例如,当随机误差绝对值由10%增加至20%时,不确定度由3%上升至7%,增加了4%;但当随机误差绝对值由25%增加至35%时,不确定度由12%上升到23%,增加了11%。
4.4 讨 论
受多种因素的影响,水资源承载力评价一般都具有一定的不确定性[12,15,22-23]。本文重点探讨了指标权重和指标数据对水资源承载力评价结果的影响。
以5种方法得到的权重值为原始样本,通过Bootstrap抽样以及均匀分布假设法的随机抽样发现,两种方法量化得到的新疆地区水资源承载力评价等级的不确定度分别为21%和17%,说明指标权重的不同对评价等级的识别有一定影响。因此,在确定权重的传统方法基础上有必要提出改进策略,以降低指标权重不确定性带来的评价结果不合理的风险。
以指标数据实际误差为基础生成随机误差的结果表明,由指标数据不确定性导致的研究区水资源承载力评价等级的不确定度为8%,说明数据的不确定性也影响了水资源承载力等级的识别,且指标数据的不确定性越大,其导致的评价等级的不确定度也越大。这也意味着,在未来水资源量存在极大不确定性的条件下,未来水资源承载力评价结果的准确性将在很大程度上受到影响。
通过对比权重和数据的不确定性对研究区水资源承载力的影响结果发现,当误差在10%以内时,二者的影响程度比较接近。例如,当误差绝对值为10%时,由权重导致的评价等级的不确定度不足1%,由数据导致的不确定度为3%;但当误差再继续增加时,数据不确定性对评价等级的不确定度明显增大。例如,当误差绝对值为30%时,权重导致的不确定度为6%,而由数据导致的不确定度则达到18%。这意味着在水资源承载力评价过程中,除了指标权重外,数据的可靠性也需要重点关注,有时其影响程度甚至大于指标权重,而这一点在以往研究中往往容易被忽视。
需要说明的是,为了对比权重和数据对评价结果的影响,本文设定了等幅的误差变动,但在实际工作中,并非所有数据都存在误差,且不同数据间的误差也不尽相同,因此等幅误差的设定某种程度上具有一定的假设性。同时,论文中也存在着其他不足。例如,在量化权重和数据的不确定性时,是从原始样本集中随机取样或以增加随机误差的方式来量化,由于原始样本数据较少,因此一定程度上也会影响到新样本数据的代表性;在进行研究区水资源评价时,新疆地区多年平均降水量各地相差很大,水资源承载力各地也不尽相同,但本文并未考虑该地区水资源承载力的区域差异性。
5 结 论
(1) 熵权TOPSIS评价模型结果显示,2008~2015年新疆水资源处于超载状态,从2016年开始水资源由超载状态转变为临界状态,水资源承载力适中,2018~2019年为弱承载状态,水资源进一步开发利用的潜力较大。
(2) 以5种方法确定的指标权重值为原始样本,Bootstrap方法表明,由指标权重不确定性导致的新疆地区水资源承载力评价等级的不确定度为21%;均匀分布假定的随机抽样法表明,指标权重导致的承载力评价等级的不确定度为17%。以熵权法确定的权重为基准,通过增加等幅误差的评价结果表明,随着误差绝对值的增加,研究区水资源承载力评价等级的不确定性随之增大;当误差增加一倍时,评价等级的不确定度达到25%。
(3) 以指標数据实际误差为基础生成随机误差的结果表明,由指标数据不确定性导致的研究区水资源承载力评价等级的不确定度为8%;随着数据误差绝对值的增加,评价等级的不确定性随之增大,当误差绝对值大于20%以后,评价等级的不确定度明显上升。
(4) 指标权重与数据相比,数据不确定性对研究区水资源承载力评价等级的影响更大,尤其是当数据存在较大不确定性时其影响尤为显著。这说明,在进行水资源承载力评价时,既要关注指标权重的合理性和科学性,同时也要尽可能收集权威资料,对收集到的数据进行合理性和准确性检查和判断,以减小数据不确定性对评价结果的影响。
参考文献:
[1] 王建华,姜大川,肖伟华,等.水资源承载力理论基础探析:定义内涵与科学问题[J].水利学报,2017,48(12):1399-1409.
[2] 胡永江,丁超,朱菊,等.基于文献计量学的水资源承载力研究进展综述[J].内蒙古科技大学学报,2021,40(1):91-97.
[3] 徐翔宇,郦建强,金菊良,等.基于风险矩阵的多要素水资源承载力综合评价方法[J].水利水电科技进展,2020,40(1):1-9.
[4] 李少朋,赵衡,王富强,等.基于AHP-TOPSIS模型的江苏省水资源承载力评价[J].水资源保护,2021,37(3):20-25.
[5] 胡启玲,董增川,杨雁飞,等.基于联系数的水资源承载力状态评价模型[J].河海大学学报(自然科学版),2019,47(5):425-432.
[6] 曹永强,朱明明,张亮亮,等.基于可变模糊评价法的大连市水资源承载力分析[J].水利水运工程学报,2016(4):40-46.
[7] 丁相毅,石小林,凌敏华,等.基于“量-质-域-流”的太原市水资源承载力评价[J].南水北调与水利科技(中英文),2022,20(1):9-20.
[8] 王红瑞,巩书鑫,邓彩云,等.基于五元联系数的水资源承载力评价[J].西北大学学报(自然科学版),2019,49(2):211-218.
[9] 王杰,李占玲.基于熵权的TOPSIS综合评价法在大气环流模式优选中的应用[J].南水北调与水利科技(中英文),2020,18(2):14-21.
[10] 杨海燕,付凯,孙晓博,等.基于CRITIC-GR-TOPSIS法的烟台市水资源承载力综合评价[J].水土保持通报,2021,41(2):215-221,305.
[11] 金菊良,刘东平,周戎星,等.基于投影寻踪权重优化的水资源承载力评价模型[J].水资源保护,2021,37(3):1-6.
[12] 王富强,侯新丽,王玉举,等.基于EFAST-云模型的区域水资源承载力评价[J].华北水利水电大学学报(自然科学版),2022,43(3):28-35.
[13] 刘华利.新疆维吾尔自治区塔里木河流域水资源承载力研究[J].水利水电快报,2020,41(8):8-11.
[14] 李静,王飞东,李强雷.中国中东部水资源承载力评价及障碍因子识别[J].人民长江,2021,52(6):58-64.
[15] 高玉琴,吴迪,刘海瑞,等.城市化影响下区域水资源承载力评价[J].水利水电科技进展,2022,42(3):1-8.
[16] 杜雪芳,李彦彬,张修宇.基于TOPSIS模型的郑州市水资源承载力研究[J].人民黄河,2022,44(2):84-88.
[17] 张宁宁,粟晓玲,周云哲,等.黄河流域水资源承载力评价[J].自然资源学报,2019,34(8):1759-1770.
[18] 及茹,张弦,李国胜.粮食主产区水土资源匹配、承载力及影响因素分析[J].人民长江,2021,52(8):105-112.
[19] 向梦玲,姚建.改进TOPSIS模型在沱江流域水质评价中的应用[J].人民长江,2021,52(2):25-29.
[20] 王立坤,宋瑞丽,裴巍,等.基于改进TOPSIS模型的黑龙江省西部半干旱地区农业旱灾脆弱性评价[J].东北农业大学学报,2018,49(1):66-73.
[21] 卢方园,贾德彬,高瑞忠,等.内蒙古荒漠草原灌区水资源承载力评价研究[J].灌溉排水学报,2022,41(8):39-44.
[22] 杨亚锋,王红瑞,赵伟静,等.水资源承载力的集对势-偏联系数评价模型[J].工程科学与技术,2021,53(3):99-105.
[23] 陈隽,巩书鑫,王红瑞,等.水资源系统分析中模糊隶属度与集对联系数的不确定性特征辨析[J].水电能源科学,2018,36(11):30-33.
(编辑:谢玲娴)
Abstract:
Water resources carrying capacity(WRCC)is an important rigid constraint to achieve spatial balance,and its scientific evaluation is of great importance for the construction of regional ecological civilization and sustainable development.Due to the effects of many factors,the evaluation of WRCC generally has some uncertainties,however,such uncertainty was not quantified in most of previous studies.Taking Xinjiang region as the study area,this study mainly focused on quantifying the uncertainty of WRCC evaluation caused by indicator weights and data.Bootstrap sampling,random sampling of uniform distribution hypothesis,random error generation methods were used in generating indicator weight samples and data samples.The concepts of membership degree and uncertainty degree were proposed to quantify the uncertainty in WRCC evaluation.The results showed that based on Bootstrap sampling and uniform distribution hypothesis,the uncertainty degrees of WRCC evaluation caused by the uncertain indicator weights were 21% and 17% in the study area,and that caused by the uncertain data was 8%.With the increases of uncertainty in weights and data,the uncertainty degrees of WRCC evaluation caused by them also increased.Furthermore,the data uncertainty had a greater impact on WRCC evaluation,according to the method of increasing the equal amplitude error.The research results can provide reference for regional economic development and sustainable utilization of water resources.
Key words:
water resources carrying capacity;uncertainty;weight;membership degree;uncertainty degree;Bootstrap

