破解坐标系中的“旋转”变换问题

文／江美红

同学们，当你遇到坐标系中的“旋转”变换问题时，是否感到“无从下手”或者“困难重重”？此类问题是中考的热点和难点。想要破解它，我们需结合图形自身的特点，根据旋转的性质找到旋转过程中的“变化量”和“不变量”，构造“K 字型”，利用三角形全等或相似的知识来解决。下面，让我们一起来看看“K字型”的魔力吧！

一、旋转角度为直角

1.定点绕定点旋转

例1 如图1，直线y=x+1 与x轴、y轴分别相交于点A、B，将直线AB绕点B顺时针旋转90°，在旋转后的直线上截取BC=2BA，则点C的坐标为______。

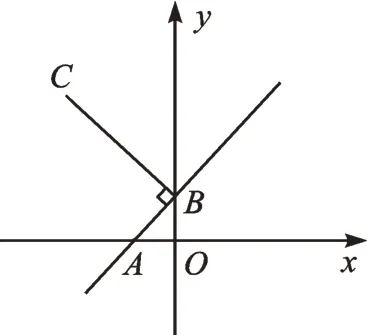
图1

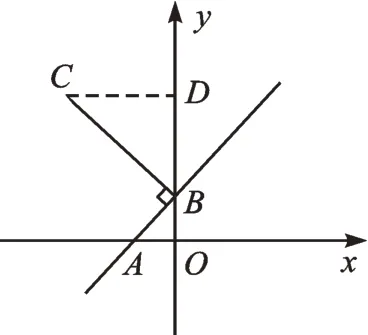
图2

【思路分析】如图2 所示，过点C作CD⊥y轴，垂足为D，构造“K 字型”。由BC=2BA，OA=1，根据△BCD∽△ABO，可得CD=BD=2，所以点C的坐标为（-2，3）。

【反思归纳】解决本题的关键是求出线段CD、BD的长度。根据∠ABC=∠AOB=90°，且BC=2BA，作CD⊥y轴构造“K 字型”，利用相似三角形的知识直接求出线段的长度，再转化为点的坐标。

2.动点绕定点旋转

例2 如图3，在平面直角坐标系中，Q是直线y=-+2 上的一个动点，将Q绕点P（1，0）顺时针旋转90°，得到点Q′，连接OQ′，则OQ′的最小值为。

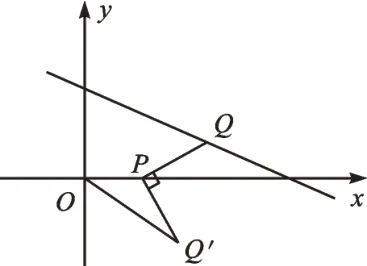
图3

图4

【反思归纳】解决本题的关键是表示出点Q′的坐标。题中点Q是直线上的一个动点，点Q′随着点Q的运动而运动。解决此类问题的策略是以“静”制“动”，将直线上的动点Q看作一个定点，设点Q的含参坐标，根据PQ=PQ′，∠QPQ′=90°，构造“K 字型”，利用三角形全等的知识得出点Q′的坐标，再构建目标函数求出最值。

3.定点绕动点旋转

例3 在平面直角坐标系中，点A的坐标是（-2，3），将点A绕点C顺时针旋转90°得到点B。若点B的坐标是（5，-1），则点C的坐标是________。

【思路分析】先画出如图5 所示的图形，再构造如图6所示“K字型”。设点C的横坐标为a，则DC=a+2，CE=5-a。根据△ADC≌△CEB，可得BE=a+2，AD=5-a，列出方程a+2+4=5-a，解得a=-，所以点C的坐标为（-）。

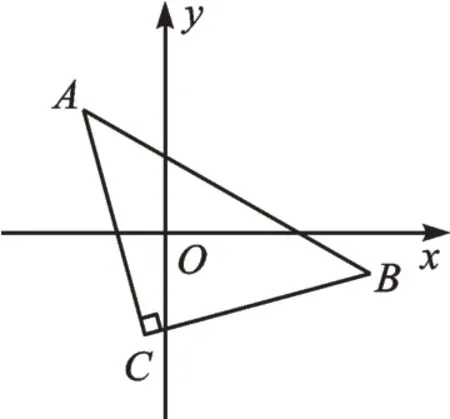
图5

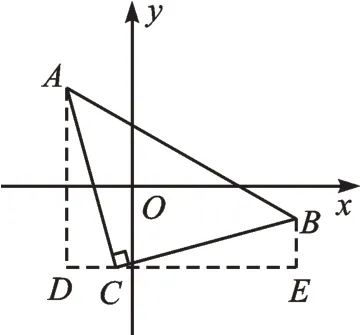
图6

【反思归纳】解决本题的关键是确定旋转中心的位置，画出图形，再构造“K 字型”，然后设点C的横坐标，利用三角形全等的知识，列出方程，得出点C的坐标。

二、旋转角度为非直角

例4 如图7，点A、点B的坐标分别为（0，4）、（3，0），将线段AB绕点A按逆时针方向旋转α得到线段AC。若tanα=2，则点C的坐标为________。

图7

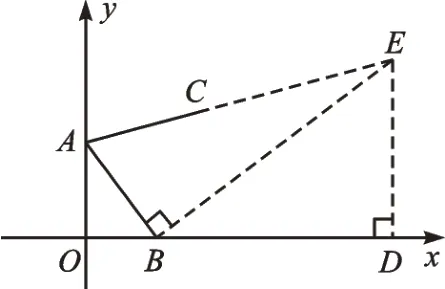
图8

【反思归纳】解决旋转角度为非直角问题的策略是通过添加辅助线，将旋转角置于直角三角形中，再构造“K 字型”来解决问题。这里也可过点C作AC的垂线，但因点C坐标未知，所以在点C处构造“K 字型”解决问题较上面方法会烦琐一些。

通过以上四道例题的分析，同学们是否找到了破解坐标系中“旋转”变换问题的妙招？构造“K 字型”是快速攻破此类问题的关键。若旋转角度为直角，则可直接构造“K 字型”，利用三角形全等或相似的知识解决问题；若旋转角度为非直角，则先作出直角，转化为旋转角度为直角的问题。同学们在平时的学习中，要善于总结解题策略，做到“会一道，通一类”，提升学习效果。