GEO SAR天线波束指向定标中的误差分析

邢楷初，王 宇，洪 峻，邱 天

（1.中国科学院空天信息创新研究院，北京 100190；2.中国科学院微波成像技术国家重点实验室，北京 100190；3.中国科学院大学，北京 100049）

0 引 言

近些年来，地球同步轨道合成孔径雷达（Geosynchronous Orbit Synthetic Aperture Radar，GEO SAR）受到了诸多关注，相比于星载低轨SAR，GEO SAR 可以有效缩短重访周期，并大幅提升测绘带宽度。目前，国际上的航天强国都在积极开展GEO SAR 的研究［1-2］。我国预计于2022年发射全球第一颗L 波段20 m 分辨率的GEO SAR 卫星，将服务于减灾、国土、地震和海洋等多个微波遥感应用领域。SAR 辐射定标是上述应用准确性和前提，天线波束指向定标是GEO SAR 系统定标的关键技术之一［3］。

GEO SAR 运行于小倾角地球同步轨道，搭载反射面天线，相比于低轨SAR，其距离向波束宽度仅有0.58°，测绘带宽度最大达到3 000 km，合成孔径时间可达千秒量级，并且受地球自转影响严重，在合成孔径时间里，卫星的运动轨迹不再是直线，而是曲线运动轨迹［4］，这些特点使得GEO SAR 系统定标特别是天线波束指向定标与低轨SAR 系统存在明显区别。

目前，针对低轨SAR 系统的天线波束指向定标方法主要有三种：1）点目标法；2）均匀分布目标法；3）地面接收机法。第一种方法将一组经过精确标定的点目标（如无源角反射器和有源定标器）放置于测绘带内，从SAR 图像中测量这些点目标的能量响应，并根据响应值测量距离向指向，实现波束指向定标，在实际应用中点目标法的定标精度较低，难以达到GEO SAR 的波束指向定标精度需求。第二种方法利用大范围散射特性稳定的地面均匀分布目标的SAR 图像数据测量距离向指向，均匀分布目标法要求分布目标的范围能够覆盖整个测绘带宽并具有稳定的散射特性，位于南美洲的亚马逊雨林是诸多先进SAR 任务中使用最广泛的分布目标［5］。第三种方法将经过精确标定的地面接收机放置于测绘带内，对接收机记录的数据进行处理重建方位向天线方向图，并与理想方向图比对实现方位向指向定标，但GEO SAR 在合成孔径时间内天线方向图（距离向和方位向）二维耦合，这与低轨SAR 系统有很大区别。对于同样搭载反射面天线的地球同步轨道通信卫星（GEO 通信卫星），常用的波束指向测量方法主要分为两类：1）基于相位的测量方法；2）基于幅度的测量方法。第一类方法主要是比相单脉冲，理论上可以获得极高的波束指向测量精度，但在工程上却不易实现。第二类方法包括最大信号法和比幅单脉冲法，目前在轨应用的波束指向测量技术大多基于后者［6］。针对GEO SAR 系统，航天科技集团五院在比幅单脉冲测向方法的基础上，提出了一种基于多脉冲分时比幅的天线波束指向定标方法［7］，但是该方法并没有对GEO SAR 天线波束指向误差进行分析，并且国内外对于GEO SAR的研究多集中于成像算法和系统设计，针对GEO SAR天线波束指向误差的研究相对较少。

本文在基于多脉冲分时比幅的天线波束指向定标方法基础之上，对可能影响波束指向定标精度的误差源进行研究，依次对卫星姿态测量误差、三维系统性误差以及指向定标方法引入的指向误差进行了分析。本文余下章节安排如下：第1节给出了GEO SAR 波束指向的定义，分析了GEO SAR波束指向的特点，并介绍了基于多脉冲分时比幅的GEO SAR 天线波束指向定标方法；第2 节详细推导了卫星姿态测量误差、三维系统性误差以及指向定标方法引入的指向误差的仿真机理；第3节结合GEO SAR 系统参数及卫星姿态数据对各误差项引入的指向误差进行了仿真实验和分析；第4节给出结论。

1 天线波束指向定标方法

1.1 天线波束二维指向

GEO SAR天线波束指向是二维的指向，包括距离向指向和方位向指向，首先给出二维指向的定义。

如图1所示，卫星星下点连线SO与视轴ST的夹角定义为距离向指向θR，卫星速度方向VS与视轴方向ST的夹角定义为方位向指向θAZ。其中，卫星相对地球的运动在地心地固坐标系中进行描述，该坐标系以地心为坐标系原点，X轴位于赤道平面内，正方向指向格林尼治子午线，Z轴为地球自转轴，正方向指向北极点，Y轴与X轴和Z轴构成右手坐标系。

图1 GEO SAR天线波束二维指向

在地心地固坐标系下，卫星星下点连线SO的表达式为

式中，

卫星速度矢量VS的表达式为

视轴矢量ST的表达式为

式（1）～（9）中，a是轨道长半轴，f是真近点角，e是轨道偏心率，i是轨道倾角，ω是近地点幅角，Ω是升交点赤经，ωe是地球自转角速度，t是卫星运行时间，μ是地球引力常数，ϕP是卫星俯仰姿态角，ϕR是卫星滚动姿态角，ϕY是卫星偏航姿态角，θL是波束中心视角，符号含义下同。

距离向指向定义为星下点连线和视轴的夹角，方位向指向定义为卫星速度与视轴的夹角，则地心地固坐标系下，距离向指向为

方位向指向为

1.2 GEO SAR天线波束指向变化特点

从式（10）和式（11）可以看出，GEO SAR 波束指向与卫星轨道、姿态以及波束中心视角紧密相关。表1给出了GEO SAR 轨道和系统参数，表2给出了GEO SAR 条带模式下某一波位参数，结合表1、表2参数可以得到GEO SAR 条带模式下一个合成孔径时间内的波束二维指向变化曲线，如图2所示。

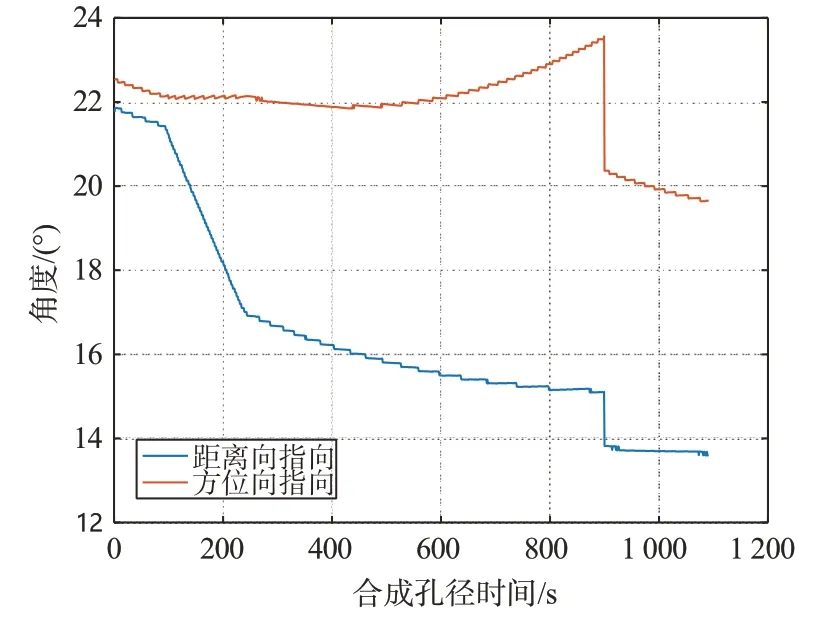
图2 条带模式下GEO SAR波束指向变化

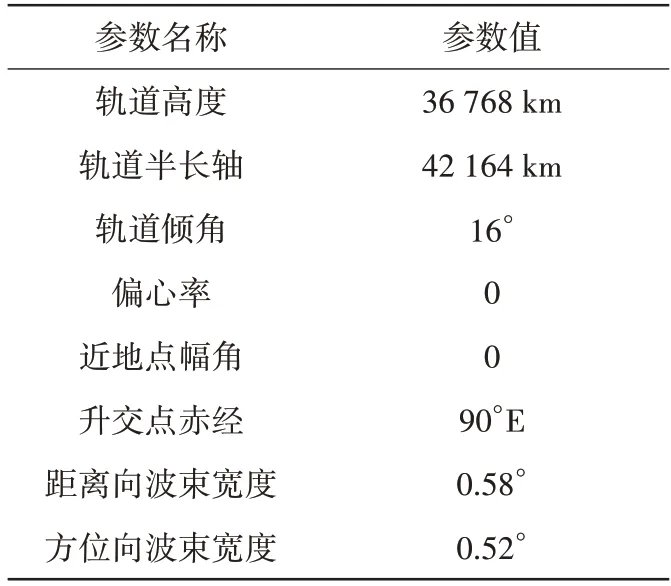
表1 GEO SAR参数

表2 波位参数

图2中可以看出GEO SAR 即使工作于条带模式，距离向指向和方位向指向在长合成孔径时间内非线性变化，这与低轨SAR 系统天线波束指向在合成孔径时间内相对不变有很大区别。在低轨SAR 系统中利用放置于测绘带内地面接收机重建的方位向天线方向图可以完成方位向指向定标，指向定标精度可以达到0.001°数量级。该方法隐含的前提条件是SAR 天线方位向方向图和距离向方向图不存在耦合，同波位下二维波束指向与二维波束指向偏差一一对应，但GEO SAR 在合成孔径时间内处于变速曲线运动，其二维指向变化非线性，二维天线方向图严重耦合，同波位不同时刻波束指向变化，不能通过二维固定指向偏差描述天线波束指向误差，所以低轨SAR 系统波束指向定标方法不适用于GEO SAR系统。

1.3 GEO SAR天线波束指向定标方法

航天科技集团五院针对GEO SAR 系统在比幅单脉冲测向方法的基础上，采用基于多脉冲分时比幅的波束指向定标方法，定标原理如图3所示，主要由星上分时产生的4 个信标波束和1 个单天线地面接收机组成。地面接收机布设于4 个信标波束的中心位置，如图3（a）所示，图3（b）中给出了信标脉冲信号的处理方法，GEO SAR 天线通过不同馈源组合形成4个信标波束，分别为距离向左右对称两个信标波束和方位向左右对称两个信标波束，并依次向地面接收机发送信标脉冲信号，接收机接收信标脉冲信号后，经过和差波束处理可以分别估计GEO SAR 天线波束距离向和方位向指向偏差，从而实现天线波束指向定标。

图3 基于多脉冲分时比幅的波束指向方法

但该方法并没有考虑影响GEO SAR 天线波束指向定标的误差因素，仅论证了该方法实现的可能性，在实际应用中，必须对各项指向误差源进行定量分析，深入探讨各项误差引入的指向误差对天线波束指向定标精度的影响。

2 误差源组成

影响GEO SAR 天线波束指向定标精度的误差源主要分为三类：

1）卫星姿态测量误差

GEO SAR 卫星通过星敏感器来确定卫星在空间的位置和三轴姿态，星敏感器受空间光源的影响导致卫星姿态的确定在偏航、俯仰和滚动三个方向上存在测量误差，鉴于GEO SAR 卫星作用距离远，卫星姿态测量误差对波束指向定标精度的影响不可忽视。

2）三维系统性误差

主要包括阵面形变误差、馈源一致性误差、姿态控制误差、天线安装误差等，考虑到GEO SAR 天线方向图是馈源初级方向图和反射面口径场方向图合成得到的远场方向图［8-9］，并且波束指向与卫星姿态紧密相关，因此阵面形变误差和馈源一致性误差对天线波束指向的影响与姿态控制误差和天线安装误差可以综合视为天线相对于卫星本体坐标系的系统性安装姿态误差，即三维系统性误差。

3）指向定标方法的测量误差

主要由通道增益稳定性和接收机热噪声组成。对于通道稳定性，包括星上馈源通道增益稳定性和接收机通道增益稳定性，工程上可以实现接收机的通道增益稳定性优于0.2 dB，所以本文主要分析馈源通道增益稳定性对天线波束指向的影响。

在本节中，依次对卫星姿态测量误差、三维系统性误差和指向定标方法的影响机理进行详细分析。

2.1 卫星姿态测量误差引入的波束指向误差

卫星姿态通常在卫星飞行坐标系中进行描述，该坐标系的坐标原点位于卫星质心，X轴指向卫星速度矢量方向，Z轴在卫星运行轨道平面内指向地心，Y轴与X轴和Z轴构成右手坐标系。卫星的姿态测量误差可以用滚动姿态测量误差ΔϕR、俯仰姿态测量误差ΔϕP和偏航姿态测量误差ΔϕY进行描述，进而得到波束二维指向误差，即距离向指向误差Δθr和方位向指向误差Δθaz。

已知GEO SAR 波束中心视角为θL，则波位预设指向矢量为=[0,sinθL,cosθL]T。

卫星姿态测量误差使得波束指向偏离预设指向，此时波束指向矢量变为

式中，

则由卫星姿态测量误差引入的距离向指向误差为

引入的方位向指向误差为

2.2 三维系统性误差引入的波束指向误差

设三维系统性误差表示为(θr0,θp0,θy0)，其中θr0为滚动轴系统性误差，θp0为俯仰轴系统性误差，θy0为偏航轴系统性误差。三维系统性误差对GEO SAR 波束指向的影响表现为由一个三维坐标（3 个姿态轴的系统性误差）转变为一个二维坐标（波束二维指向误差）。

卫星姿态通过滚动姿态角ϕR、俯仰姿态角ϕP、偏航姿态角ϕY进行描述，并假设卫星姿态测量误差对波束指向的影响已经消除，经过姿态旋转后，预设波束指向矢量为

此时，距离向指向θR和方位向指向θAZ分别为

三维系统误差会导致波束指向偏离预设值，波束指向矢量变为

则由三维系统性误差引入的距离向指向误差为

引入的方位向指向误差为

2.3 指向定标方法的测量误差

2.3.1 和差比幅测角原理

和差比幅测角技术广泛应用于雷达系统中，GEO SAR 采用的基于多脉冲分时比幅的指向定标方法本质上也属于和差比幅测角技术。利用两个相同且彼此部分重叠的波束（两波束的交叠轴被称为等功率轴），并对这两个波束收到的信号进行和差处理，得到和信号和差信号，基于差信号与角度偏差值间的函数关系（测角误差信号），求得目标方向与等功率轴的角度偏差［10］。

设左、右波束方向图函数分别为f1(Δθ)、f2(Δθ)，目标方向偏离等功率轴的角度为Δθ，根据和差比幅测角原理，测角误差函数u表示为

式中，fΔ(Δθ)为差波束方向图，fΣ(Δθ)为和波束方向图。

在等功率轴附近，测角误差信号u与目标方向偏离等功率轴的角度Δθ可近似为线性关系［9］，即

因此可由u判定Δθ的大小及方向。式（22）中，λθ是测角误差函数的斜率估计，并且λθ只与天线结构有关，当天线结构确定时，λθ即为常数；是测角误差函数u的估计值；θ0是修正常值。

2.3.2 基于多脉冲分时比幅的指向定标精度估计

GEO SAR 系统使用基于多脉冲分时比幅的波束指向定标方法，以距离向指向定标为例，星上通过不同馈源组合形成距离向左、距离向右两个信标波束，并向地面接收机发射信标脉冲信号，如图4所示。

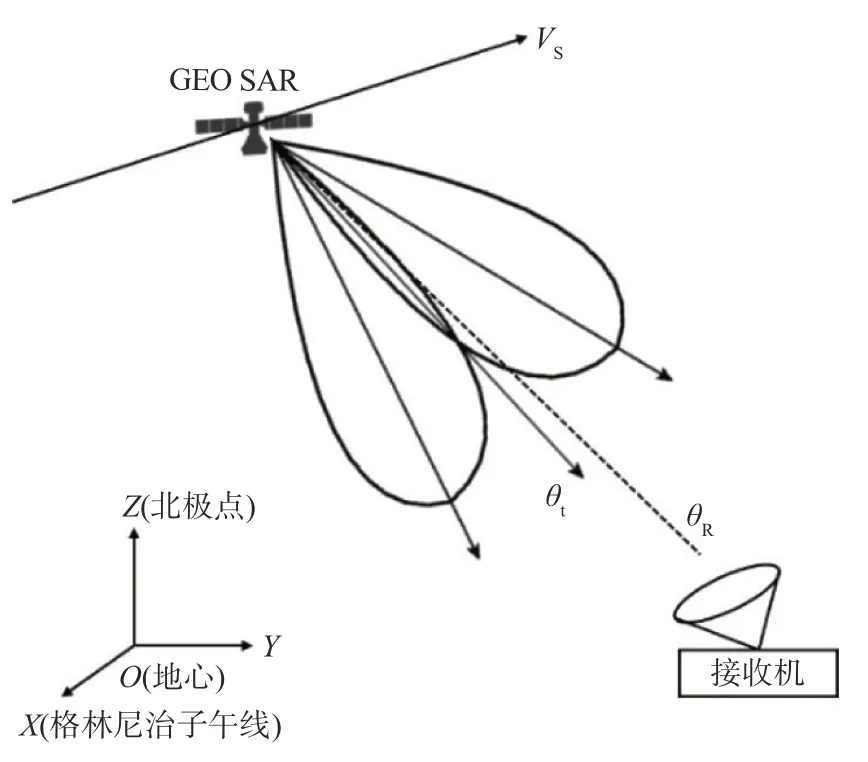
图4 距离向指向定标示意图

设GEO SAR 距离向预设指向为θR，前面分析可知，卫星姿态测量误差和三维系统性误差会导致波束指向偏离预设值，距离向的真实指向变为θt，θt与θR间的差值即为距离向指向偏差。信标波束方向图形状实际由GEO SAR 天线参数决定，在本文中假定为高斯函数形式方向图，则距离向左、右两个信标波束在地面接收机处的方向性函数表示为

式中，θS为波束偏置角（即信标波束最大值方向偏离等功率轴的角度），θB为信标波束的半功率波束宽度，α=4 ln 2，β=-α/θ2B。

设信标脉冲信号经过地面接收机天线接收、低噪声放大、下变频和模数转换后接收到的距离向左、右两信标信号分别为V1、V2，则有

式中，g为接收机接收通道增益，G1、G2分别为星上发射距离向左右信标波束时的馈源通道增益，A为星上发射的复信标信号（线性调频信号），Z1、Z2分别为接收机接收左右两信标脉冲信号时的热噪声。并有V1={v1i}、V2={v2i}、A={ai}、Z1={z1i}、Z2={z2i}，i=1,2,…,n，均是n维列矢量，n是地面接收机采样点数。

对V1、V2进行和差处理，得到和信号VΣ、差信号VΔ，分别为

式中，VΔ={vΔi}、VΣ={vΣi}，i=1,2,…,n，也是n维列矢量；η=g[G1f1(Δθ)+G2f2(Δθ)]，u是测角误差函数，表示为

前面分析可知λθ是测角误差函数的斜率估计，可以通过拟合信标波束方向图的方法求得。将fΔ(Δθ)在Δθ=0 处进行泰勒展开，忽略二阶以上项，得到

考虑到fΔ(0)≈0（差波束的零值深度很低），式（27）可进一步表示为

当Δθ≪1 时，在等功率轴附近有fΣ(Δθ)≈fΣ(0)，所以测角误差函数u在Δθ≪1 时可以表示为

式（26）带入β并求偏导，可以得到

于是有

从式（31）中可以看出，λθ与信标波束方向图形状和馈源通道增益有关，其中信标波束方向图形状由天线结构决定，而馈源通道增益稳定性是一项随机误差。在实际应用中可以通过多个位置点的实测数据拟合得到直线的斜率，馈源通道增益稳定性会对λθ的拟合精度产生影响，进而对Δθ的估计精度产生影响。

利用似然函数可以获得测角误差函数u的估计值［11］，设地面接收机信标脉冲信号的采样点数为n，接收机热噪声是零均值高斯白噪声，方差为σ2，根据极大似然准则可推导出似然函数为

式中(*)H代表共轭转置。

对lnL(VΔ,VΣ;u,η关于u、η) 求共轭偏导，并令之为零得到

联合式（32）、式（33）求解出u的极大似然估计为

上式中给出的估计是两个相互独立的高斯随机变量的比值，根据MLE（矢量参数）的渐近特性，当n足够大时，的渐进分布可以表示为［12］

式中，～表示渐进分布于，N(a,b) 表示均值为a、方差为b的高斯分布，I(u) 为费雪信息，具体表示为

根据式（25），VΣ可以表示为

式中i=1,2,…,n。所以地面接收机的和信号信噪比可以表示为

将式（38）代入式（36）中，得到

根据2.3.1节中和差比幅测角原理，Δθ与u近似为线性关系，即，所以的渐进分布可表示为

所以由指向定标方法引入的指向误差估计为

3 仿真试验与结果分析

3.1 卫星姿态测量误差引入的波束指向误差分析

GEO SAR 卫星姿态的控制在偏航、俯仰和滚动三个方向上可能存在±0.01°固定偏差，外加0.003°姿态测量误差，这些姿态测量误差最终会引入二维指向误差。结合GEO SAR 的系统参数和2.1 节中的影响机理，仿真分析了卫星滚动、俯仰和偏航姿态测量误差可能引入的波束指向误差，仿真结果如图5所示。其中，图5（a）为滚动姿态测量误差引入的二维指向误差，图5（b）为俯仰姿态测量误差引入的二维指向误差，图5（c）为偏航姿态测量误差引入的二维指向误差。

图5 卫星姿态测量误差引入的二维指向误差

从图5中可知，距离向指向误差主要由滚动姿态测量误差引起，而方位向指向误差则主要由俯仰姿态测量误差引起，偏航姿态测量误差对方位向指向也有较大影响，0.003°的卫星姿态测量误差分别会引入0.003°的距离向指向误差和0.0033°的方位向指向误差。

3.2 三维系统性误差引入的波束指向误差分析

结合表2条带模式波位参数和卫星姿态数据对三维系统性误差对天线二维指向的影响进行仿真分析，并且忽略卫星姿态误差对波束指向的影响，仿真结果如图6所示。其中，图6（a）为滚动轴系统性误差引入的二维指向误差，图6（b）为俯仰轴系统性误差引入的二维指向误差，图6（c）为偏航轴系统性误差引入的二维指向误差。

图6 三维系统性误差引入的二维指向误差

从图6中可知，滚动、俯仰、偏航三个系统性误差都会对距离向指向产生不同程度的影响，滚动轴系统性误差对其影响最大；方位向指向主要由俯仰轴系统性误差引起，偏航轴系统性误差对其也有较大影响。综合考虑天线安装误差、阵面形变误差、馈源一致性误差以及姿态控制误差等因素，三维系统性误差通常为0.2°～0.5°，鉴于GEO SAR 的波束指向定标精度需求为0.01°，三维系统性误差是GEO SAR 天线波束指向定标中的主要定标对象。

3.3 指向定标方法引入的指向误差分析

仿真实验中，GEO SAR系统参数如表1所示，信标脉冲信号形式为线性调频信号，中心频率为1.25 GHz。信标波束方向图为高斯函数形式，信标波束半功率波束宽度θB=0.6°，左右对称两信标波束的中心偏置角θS=0.3°，单次估计的信标信号采样点数n=100，指向定标方法的系统测量范围定义为［-0.3°,0.3°］，仿真实验采用蒙特卡洛方法，下文中所得指向误差均由1 000 次独立的仿真结果统计获得。

3.3.1 接收机信噪比引入的指向误差分析

仿真实验中假定通道稳定性导致信标波束增益变化分别优于0，1 和2 dB，图7给出了系统测量范围内的距离向指向误差随接收机信噪比变化的曲线。

图7 接收机信噪比引入的指向误差

由图7可以看出，随信噪比的提升，因为信噪比引入的指向误差逐渐减小，当SNR≥30 dB 时，引入的指向误差已经低于0.002°；当SNR≥35 dB 时，继续提高信噪比对指向误差的改善已经不再显著。

3.3.2 通道增益稳定性引入的指向误差分析

仿真实验中假定接收信噪比分别为0，20 和40 dB，图8给出了系统测量范围内的距离向指向误差随通道增益稳定性变化的曲线。

图8 通道增益稳定性引入的指向误差

由图8可以看出，随着通道增益稳定性的恶化，由通道增益稳定性引入的指向误差逐渐增加，当通道增益变化ΔG≥1 dB 时，指向误差恶化加剧，而通道增益稳定性优于1 dB 时，通道稳定性的影响较小。综合图7和图8，接收机信噪比是影响波束指向定标方法测量精度的主要因素，当SNR≥35 dB、通道增益稳定性优于1 dB 时，GEO SAR 指向定标方法引入的指向误差小于0.001°。

4 结束语

本文针对GEO SAR 采用基于多脉冲分时比幅的天线波束指向定标方法，对可能引入指向误差的误差源进行了分析，针对卫星姿态测量误差、三维系统性误差和指向定标方法对天线波束指向的影响机理进行了详细推导，并结合GEO SAR 参数和姿态数据进行了仿真实验和定量分析。实验结果揭示了影响GEO SAR 天线波束指向的主要因素是三维系统性误差，如何针对三维系统性误差进行定标是值得进一步研究的问题。本文的研究为GEO SAR 天线波束指向定标提供了参考，对GEO SAR 系统设计、定标设计和定标处理有创新和借鉴意义。