上海市某防汛墙的安全性诊断
苑敏哲 夏才初 王兴开
(1.绍兴文理学院, 浙江绍兴 312000; 2.宁波大学, 浙江宁波 315000)
上海市地处长江三角洲交汇处,三面临海,易受台风、暴雨以及高潮、洪涝等灾害。[1-2]同时,城市经济的高速发展对上海抵御灾害风险的要求日愈提高。防汛墙在抵抗洪涝灾害中起到了非常大的作用,随着防汛墙使用年限的增长,墙体出现老化、破损、倾斜等情况,部分墙体甚至出现沉降、裂缝、坍塌等破坏性损伤。[3]这些由环境条件变化引发的安全隐患逐年在上升,在突发性破坏或积累性损伤等多重因素的叠加下,防汛墙的使用年限和安全性能状况令人担忧,为使防汛墙发挥其实际价值,保障社会生产生活和经济可持续发展,对防汛墙的完整性进行检测和安全性判断,显得尤为重要。
目前,对防汛墙安全性分析常用的手段有基于有限元分析软件的有限单元法分析法、刚体极限平衡分析法、敏感因子法分析等。张聪提出将数值分析与经典极限分析相结合的有限元分析方法,验证了有限元分析方法在岩土工程中的有效应用,为岩土工程建设和发展提供有力支持。[4]文献[5-6]介绍了采用有限元分析软件PLAXIS和同济启明星软件对黄浦江防汛墙分析的情况,对基坑施工是否影响周边围护结构墙体位移和基坑坑底隆起、危及建筑物安全,进行了稳定性分析,以此维护防汛设施的整体安全性。任敏以上海世博园防汛墙驳岸工程为例,介绍了高压旋喷法施工的特点,结合工程实例说明此工艺在经济和技术上的显著优势,为防汛墙的维护加固工程提供了借鉴和参考。[7]卢伟华结合上海黄浦江防汛墙的实际工程情况,运用敏感因子法对所选的敏感因子进行敏感性分析,求出防汛墙结构整体稳定和渗流稳定的临界值,从而进一步评判防汛墙的整体结构稳定性。[8]张琳琳等从堆载的影响因子和非堆载的影响因子两方面入手,研究并得出墙后堆载下高桩承台式防汛墙的变形规律,为防汛墙墙后堆载限制的制定提供了理论基础。[9-10]
课题所涉及防汛墙工程位于上海市一码头,由于长期以来超重船只的停靠及岸边堆载等诸多因素的影响,防汛墙产生向河道内的位移,显露墙段长度大约长20 m,墙体与原有相邻水平地面发生分离,分离量最大达80 mm。为了更加准确地对防汛墙的完整性进行评估,确保防汛墙结构安全性,保障检测结果切合工程实际,在现场勘测的基础上,运用力学分析与数值模拟相互结合的方法对防汛墙体进行承载力验算,通过对比分析实际地坪标高和设计地坪标高下墙顶受力值和理论值的大小,对防汛墙安全性进行诊断。
1 对既有防汛墙的现场勘测
1.1 工程概况
待检测段防汛墙位于上海市蕴藻浜左岸,其全景如图1所示。实测防汛墙墙顶到地面的距离约为2.7 m,墙顶宽度约为0.3 m。防汛墙结构为高桩承台(图2),防汛墙结构顶面标高为6.800 m,底面标高为2.550 m,设计地面标高为4.800 m。防汛墙顶部宽度约为0.3 m,码头设计吨位为100 t,在0~6 m宽度范围内防汛通道禁止堆载,6~10 m宽度范围内的设计荷载为10 kN/m2。
根据防汛墙的现场情况,对防汛墙与地坪的脱开、倾斜和墙体表面裂缝情况进行了现场量测。量测的防汛墙范围为14.0 m长,防汛墙平面布置如图3所示

图1 待检测段防汛墙全景Fig.1 An overall view of the detected flood control wall
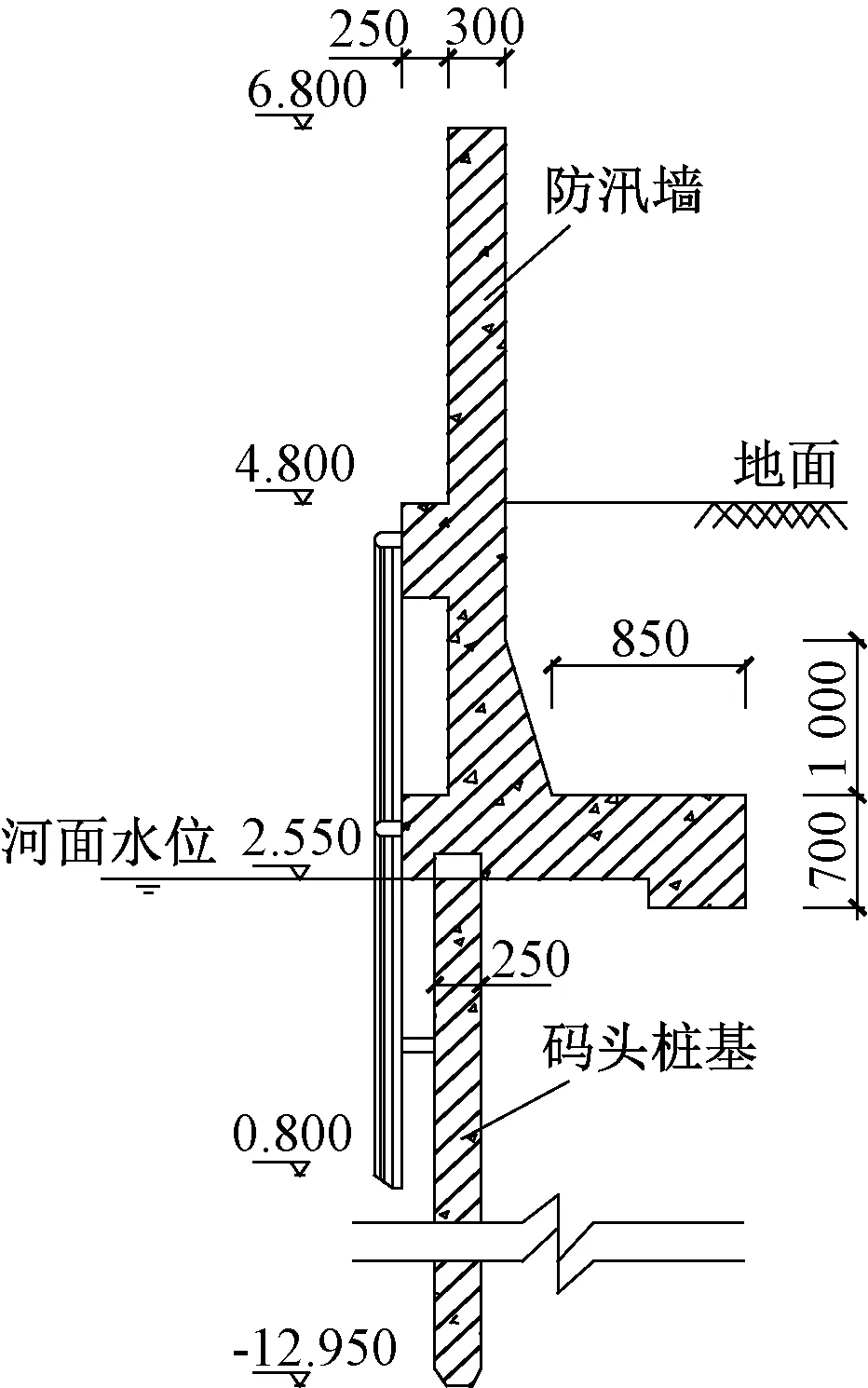
图2 防汛墙结构 mmFig.2 Structure of the flood control wall

图3 待检测段防汛墙的平面 mmFig.3 A plan of the flood control wall be detected
1.2 防汛墙与地坪的脱开
根据现场观测,明显可见被检测段防汛墙与地坪脱开。采用手工测量的方法,对脱开距离进行测量。从被检测段防汛墙最左端(F—F断面)开始,每隔0.5 m对防汛墙与地坪的脱开进行测绘,测绘结果见表1。

表1 被检测段防汛墙与地坪脱开距离Table 1 Space between the detected flood control wall and ground
由统计结果可知:整个被检测段防汛墙由左端起,脱开距离逐渐增大,与地面脱开最大处位于防汛墙的右半段,最大处为80 mm。
1.3 墙身裂缝检测
被检测段防汛墙整体基本完好,沿墙面勘察,发现在距离被检测段防汛墙左端约3.5,6.0 m处顶部有一处剥离(图4),深度不大于50 mm,被检测段防汛墙其他部位无可见裂缝。

图4 防汛墙顶的混凝土剥离Fig.4 Stripped concrete at the top of the flood control wall
1.4 倾 斜
采用铅垂线的方法对被检测段防汛墙露出地表部分的倾斜情况进行测量,在距被检测段防汛墙顶面内侧0.16 m处放下一铅垂线,在防汛墙距离地面0.20 m处测得铅垂线距离防汛墙的距离。通过换算得出防汛墙总的倾斜情况,图5是所测6个测点处防汛墙的剖面,根据测量结果显示,最大倾斜发生在被检测段防汛墙最右端的A—A剖面。从现场情况来看,被检测段防汛墙向外侧倾斜最大值为13.0 mm。
假设防汛墙下的桩基顶端是固定的,防汛墙刚性转动,根据防汛墙的高度(4.25 m)可计算出被检测段防汛墙顶部向外倾斜的倾斜值(表2)。

表2 防汛墙顶部的倾斜度Table 2 Degrees of sloping at the top of the flood control wall
2 既有防汛墙结构稳定性的简易力学分析
防汛墙完整性检测勘测现场条件复杂,干扰仪器测试结果的因素较多,加上墙体本身宽度较窄(约0.3 m),对现场测试有一定的限制。为了对防汛墙的完整性作出准确的评价,对防汛墙结构预先进行力学计算分析。
2.1 力学分析模型建立
根据现场勘测结果,墙顶的水平偏移量在A—A测试断面处最大,为22.1 mm,因此A—A断面是最不利的断面,以此作为结构受力分析的典型断面,A—A断面的结构尺寸如图6所示。

图6 防汛墙结构尺寸 mmFig.6 Dimensions of the flood control wall
沿走向取每延米防汛墙作为研究对象进行受力分析,将其简化为悬臂梁结构,下端为固定约束,承受侧向土压力三角形分布荷载和顶部受沉船拉拽作用的集中荷载,受力简图如图7所示。

图7 防汛墙力学分析模型 mmFig.7 Mechanical analysis model of the flood control wall
2.2 防汛墙内力分析
根据地层资料,土层参数取值见表3。

表3 土层参数取值Table 3 Values of soil parameters
由此计算出作用在防汛墙墙后的主动土压力[11-12]:
墙后主动土压力系数为:
(1)
式中:Ka为主动土压力系数。
则墙后主动土压力为:
(2)
式中:z为土的计算深度。
即防汛墙每延米所受到的土压力分布荷载集度为0.43 kN/m。由悬臂梁内力和变形的关系可得,三角形分布荷载作用下的梁端挠度为:
(3)

由于该值与实测墙顶变形相比可忽略不计,故仅须计算在集中力作用下的变形。
按底部固定约束的悬臂梁模型计算,当墙顶发生22.1 mm水平位移时,通过试算的方法,调整墙顶集中力的大小使其达到墙顶位移要求,得出防汛墙结构尺寸突变处1—1截面受到的剪力为F=58 kN,弯矩约为M=159.5 kN·m;防汛墙底部2—2截面受到的弯矩约为217.5 kN·m。
2.3 最不利节截面承载力验算
2.3.11—1斜截面受弯承载力计算
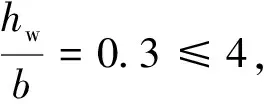
2.3.21—1正截面受弯承载力计算
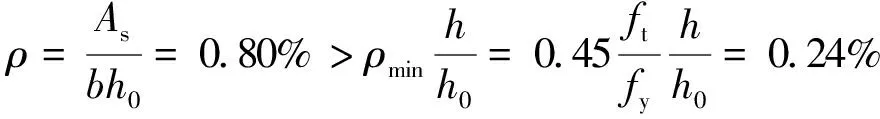
混凝土受压区高度:
(4)
式中:ξb为相对界限受压区高度;fy为纵向钢筋的抗拉强度设计值;α1为受压区混凝土矩形应力图的应力值与混凝土轴心抗压强度设计值的比值。
截面受弯承载力设计值:
(5)
由于Mu=159.60 kN·m>M=159.5 kN·m,因此截面符合承载力要求,不会被破坏。

3 防汛墙承载力有限元数值模拟分析
根据现场勘测结果计算得到的墙顶水平位移(表2),在有限元模型中采用试算的方法,调整墙顶集中力的大小使得墙顶水平位移与实测值相符,则此时的集中力就是防汛墙所受沉船的拉拽作用力,从而确定防汛墙承受的内力,验算防汛墙结构是否被破坏。
3.1 力学分析模型建立
采用有限元软件Plaxis进行计算分析。在有限元模型中,防汛墙结构和下部的桩均采用实体单元来模拟,取A—A断面,于墙顶施加一集中力来模拟防汛墙所受沉船的拉拽作用。由于防汛墙沿纵向结构形式是一致的,结构所受外力都是垂直于纵轴方向的,且外力的分布规律沿墙体纵向是均匀的,故在建立有限元模型时,沿高度方向取模型范围为30 m,沿宽度方向取模型范围为20 m,所有结构均采用15结点三角形单元,土体采取摩尔-库仑模型。实际地坪标高下,防汛墙计算沿纵向取单位长度,顶部宽度为0.3 m,墙顶离地面之间的距离约为2.7 m(有限元计算模型如图8所示)。
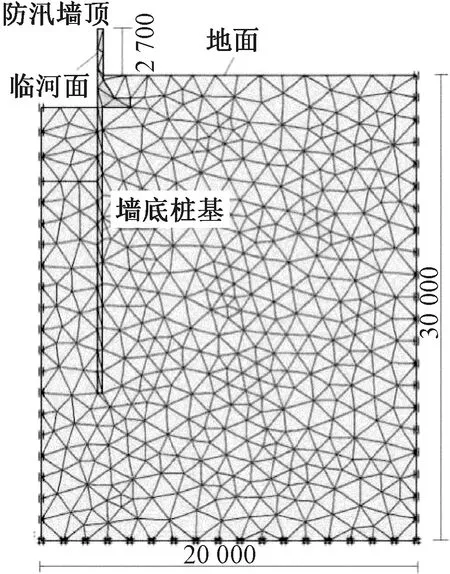
图8 有限元计算模型 mmFig.8 The finite element calculation model
3.2 参数选取
参考该地区的地质资料,土层的参数采用该地区的经验值(表4)。

表4 物理力学参数计算取值Table 4 Calculated values of physical and mechanical parameters
模拟过程:计算时防汛墙首先在土体自重应力下达到初始平衡状态,然后在顶部施加集中力荷载P,逐渐增加P值的大小,直至防汛墙顶部发生实际量测出的位移,计算此时墙身控制截面的内力。
3.3 模拟结果分析
调整作用在防汛墙顶部集中力的大小,以达到墙顶限制最大位移,墙体水平位移云见图9。
根据有限元计算结果可知:实际地坪标高下防汛墙顶部受到沉船集中力荷载作用时,控制截面1—1处的剪力为42.36 kN,弯矩值为112.68 kN·m。通过有限元法计算出的剪力与弯矩值比力学分析得出的数值较小,因此该防汛墙可以满足墙体承载力要求,不会产生断裂情况。
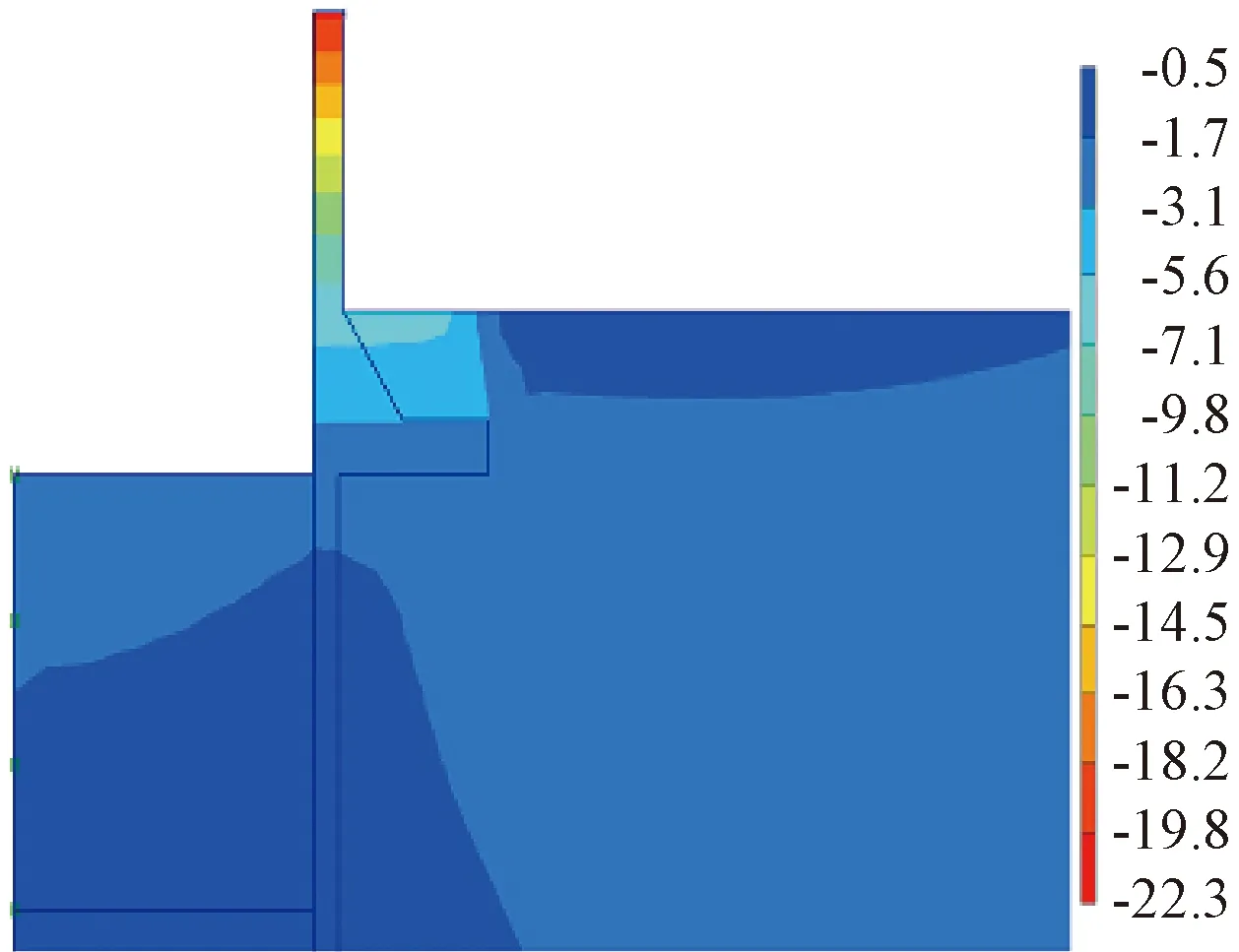
图9 按实际地坪标高计算,墙顶水平位移为22.1 mm时墙体的水平位移云 mmFig.9 Contours of horizontal displacement for the wall with a 22.1 mm horizontal displacement at the top calculated based on the actual ground level
3.4 设计地坪标高下防汛墙的数值模拟验算
根据防汛墙设计图纸,墙顶标高为6.800 m,地面标高为4.800 m,墙顶离地面之间的距离约为2.0 m,小于实际地坪标高下墙顶离地面之间的距离,因此须要建立新模型来计算设计地坪标高下的防汛墙受力情况。前文通过力学分析和有限元分析已经得出实际地坪标高下防汛墙的承载力情况,现对设计地坪标高下的防汛墙承载力进行有限元分析,利用反演得到的内力进行承载力校核。
3.5 设计地坪标高下防汛墙的数值模拟结果分析
其结构水平位移云见图10,墙顶发生22.1 mm水平位移时,根据有限元计算结果得知墙身1—1截面承受的剪力为50.85 kN,弯矩为135.25 kN·m。
结合前文的计算结果进行分析,不同情况下防汛墙墙顶水平位移和控制截面内力结果见表5。

图10 设计地坪标高下,墙顶水平位移为22.1 mm时墙体水平位移云 mmFig.10 Contours of horizontal displacement for the wall with a 22.1 mm horizontal displacement at the top calculated based on the design ground level
综上所述,实际地坪标高下和设计地坪标高下所承受的剪力与弯矩值均小于理论值,故防汛墙结构能承受集中力荷载。虽然墙体发生较明显的水平位移,但墙体结构仍然完整,无断裂之虞。
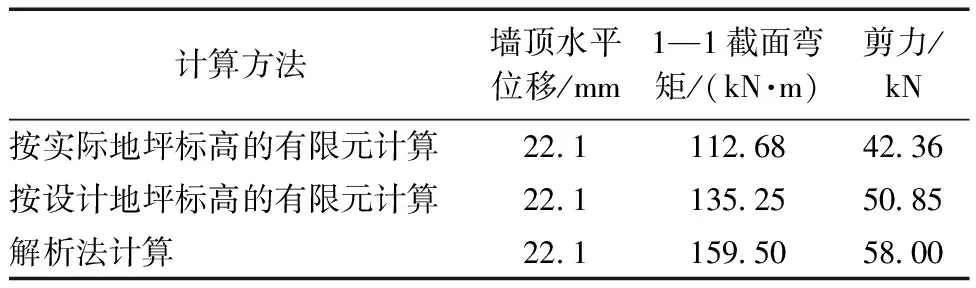
表5 不同情况下防汛墙顶水平位移和控制截面内力Table 5 Horizontal displacement at the top of the wall and the internal force in the control section in different conditions
4 结束语
1)通过力学分析,由理论计算可得,当墙顶发生22.1 mm水平位移时,最不利截面1—1受到的剪力小于截面限制条件,弯矩小于截面受弯承载力设计值。截面配筋率满足配筋要求,因此防汛墙满足承载力要求,混凝土结构不会破坏。
2)防汛墙按实际工程地坪标高进行数值模拟,顶部受到沉船集中力荷载作用时,最不利截面所承受的剪力、弯矩值均小于理论值控制值;故防汛墙能满足承载力要求,不会产生断裂。
3)防汛墙按设计地坪标高进行数值模拟,墙顶发生22.1 mm水平位移时,最不利截面承受的剪力、弯矩均小于理论值;防汛墙结构能承受集中力荷载。虽然墙体发生较明显的水平位移,但墙体结构仍然完整,无断裂之虞。
——超集中力
—— 梁在集中力作用点处的剪力分析

