箱板装配式钢结构楼盖舒适度分析及其调谐质量阻尼器的振动控制研究*

门进杰 钟 鑫 薛 辰 兰 涛, 李 然 张 亮

(1.西安建筑科技大学土木工程学院, 西安 710055; 2.中国船舶重工集团国际工程有限公司, 北京 100121; 3.徐辉设计股份有限公司, 郑州 450000)

近年来,随着社会不断发展,人们生活水平日益提高,建筑工程的规模也在不断攀升,人们对生产、生活质量的要求也不断提高,使得由楼盖振动引发的人体舒适度问题逐渐突显出来。箱板装配式钢结构建筑,作为一种新型装配式钢结构体系,其楼盖阻尼小、质量轻,与混凝土楼盖和组合楼盖相比,在人行荷载作用下更易发生不利振动,引发用户的不适感,甚至影响结构安全。目前国内外对装配式楼盖舒适度性能的研究主要集中在混凝土楼盖和组合楼盖,但对纯钢结构体系的箱板装配式钢结构楼盖的研究较少,有必要开展对箱板装配式钢结构楼盖振动舒适度的研究。

因此,通过对箱板装配式钢结构楼盖在不同参数下舒适度的分析,同时通过加入调谐质量阻尼器(TMD)降低加速度效应,冀以解决箱板装配式钢结构楼盖的舒适度问题。

1 舒适度性能评价标准

对于建筑物来说,人在绝大部分时间内感受不到建筑物的振动即为满足舒适度要求,而满足振动舒适度要求的振动加速度水平常与振感阈值有关。英国发布的BS系列标准、德国发布的DIN系列和VDI系列标准,国际标准化组织发布的ISO系列标准中,都以不同的形式给出了振感阈值和一定的振动持续时间下对应的振动加速度水平限值,这些限值通常称为舒适度限值[1],主要用于建筑振动舒适性的评价。其中ISO标准是当今世界上最为流行的评价方法,很多国家的振动舒适度标准与ISO评价方法基本上是一致的。ISO 2631标准[2]中规定采用频率加权均方根加速度作为舒适度评价指标,且给出了频率计权曲线如图1所示。基于我国国情,沿用ISO标准给出的频率计权曲线,采用竖向振级Vlz作为评价量。从我国标准化工作的发展来看,与ISO等国际标准接轨是未来必然发展趋势。各国相关标准的评价量如表1所示。

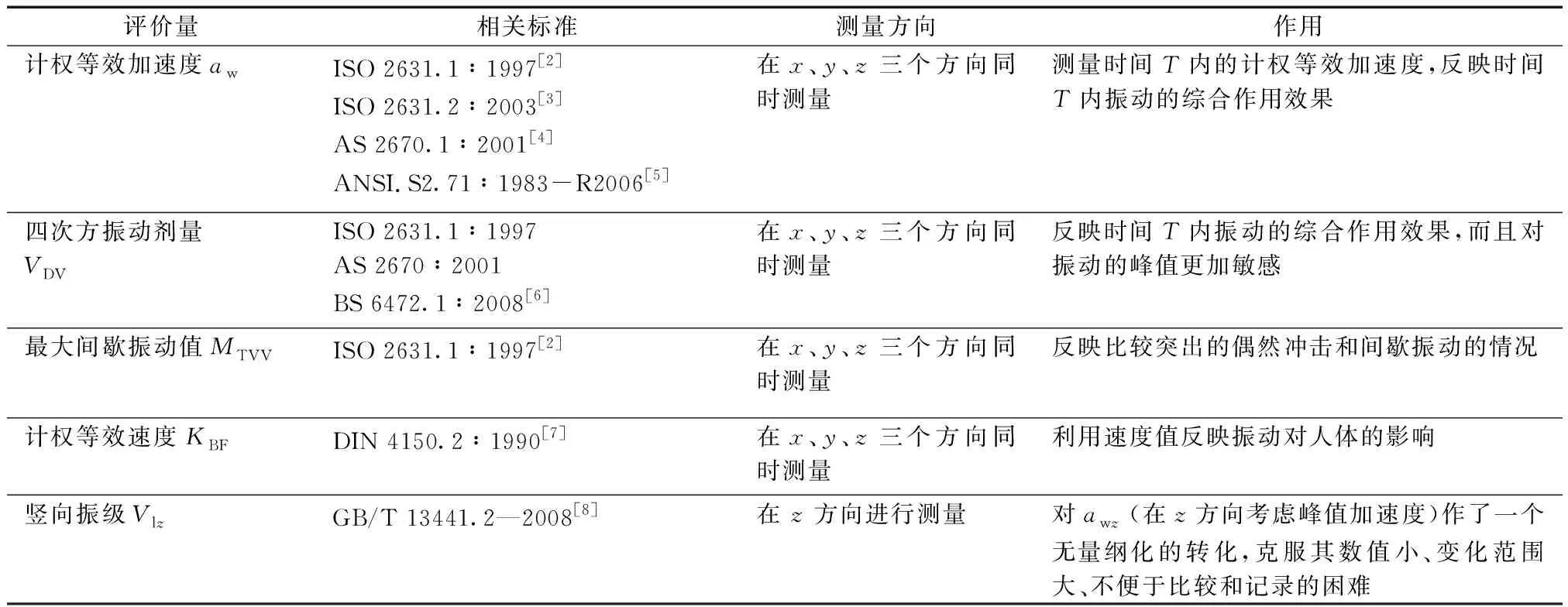
表1 各国相关标准的评价量Table 1 Evaluations of national related standards

图1 频率计权曲线Fig.1 A frequency weighting curve

2 典型箱板模块单元楼板的舒适度分析

选用有限元软件MIDAS/Gen对箱板装配式钢结构楼盖的振动特性进行分析。楼盖选用某已建箱板式钢结构住宅项目的典型尺寸。考虑到结构体系中加劲钢板墙对楼盖边缘部位的刚域效果,建模时,将楼盖上、下层钢板墙各取层高的一半,即上部和下部各取1.5 m墙高,并在墙端施加固接约束。楼盖的L型加劲肋和T型加劲肋采用梁单元,钢板采用板单元,其材质均采用Q235钢,弹性模量为206 GPa,屈服强度为235 MPa,密度为7 850 kg/m3,泊松比为0.3。结构模型如图2所示。

1—钢楼板;2—L型加劲肋;3—T型加劲肋;4—钢板墙。图2 箱板装配式楼盖模型Fig.2 A floor model of prefabricated box-plate steel structures

由振动学可知:构成振动系统的基本要素是惯性、复原性和阻尼。对于楼板振动而言,惯性、复原性可以用质量和刚度来表征,故以长宽比、钢板厚度及T型加劲肋间距为变化参数共建立了20个有限元模型,研究不同参数对箱板装配式钢结构楼板舒适度性能影响,其中T型加劲肋尺寸均为200 mm×8 mm×13 mm,L型加劲肋尺寸均为75 mm×75 mm×8 mm。具体参数设置如表2所示。

表2 模型设计参数Table 2 Model design parameters

2.1 自振特性分析

自振特性是楼盖的固有属性,与外在荷载无关。楼盖体系的自振频率综合反映了质量和刚度的变化。采用MIDAS/Gen提供的Lanczos法对楼盖进行模态分析,获得楼盖的前20阶振动模态。由于人行走时产生的振动效应主要受楼盖低阶模态的影响,楼板体系的基频所对应的能量最大。因此,针对第一阶模态进行分析,各楼盖的竖向基频如图3所示。

图3 楼盖竖向基频Fig.3 Vertical fundamental frequencies of floors

根据楼盖动力特征值分析可知:楼盖结构的基本频率均大于3 Hz,满足JGJ 3—2010《高层建筑混凝土结构技术规程》[9]要求。

2.2 确定最不利路径

从表2选取已建立的6个楼盖模型,钢板厚度为6,8,10 mm的BQ1-1、BQ1-2和BQ1-3,其长宽均为6 m×6 m,T型加劲肋间距均为1.5 m;加劲肋间距分别为1.5 m、2.0 m、3.0 m的BQ1-7、BQ2-6和BQ3-5,其长宽均为10 m×6 m,钢板厚度均为8 mm。研究人行荷载作用在楼盖的不同位置上所产生的加速度效应,由于楼盖在X方向和Y方向都是轴对称,故取其一半楼盖作为路径作用范围,具体路径布置如图4所示。其中L1～L5表示人行荷载分别作用在X方向的T型加劲肋上、T型加劲肋与L型加劲肋之间、L型加劲肋上、L型加劲肋与L型加劲肋之间、L型加劲肋与墙体之间;L6～L8表示人行荷载分别作用在Y方向的T型加劲肋与T型加劲肋之间、T型加劲肋上、T型加劲肋与墙体之间;L9表示人行荷载作用在X、Y之间斜45°方向。

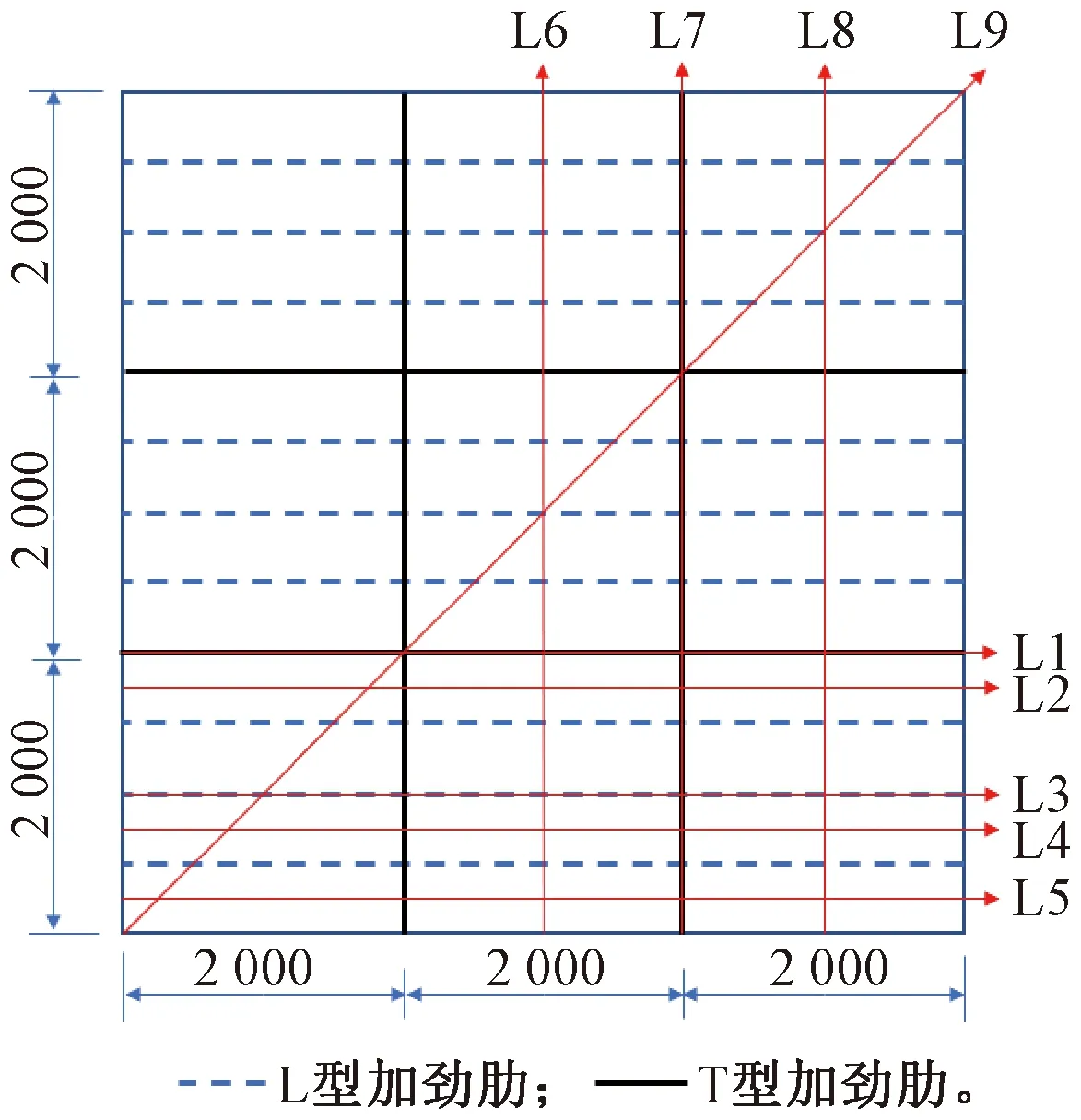
图4 行走路径 mmFig.4 Walk paths

由图5可知:不同的路径上产生不同的加速度效应,且所产生的加速度效应中,肋与肋之间的大于肋与墙体之间的,而肋条与墙体之间的大于在肋上的。

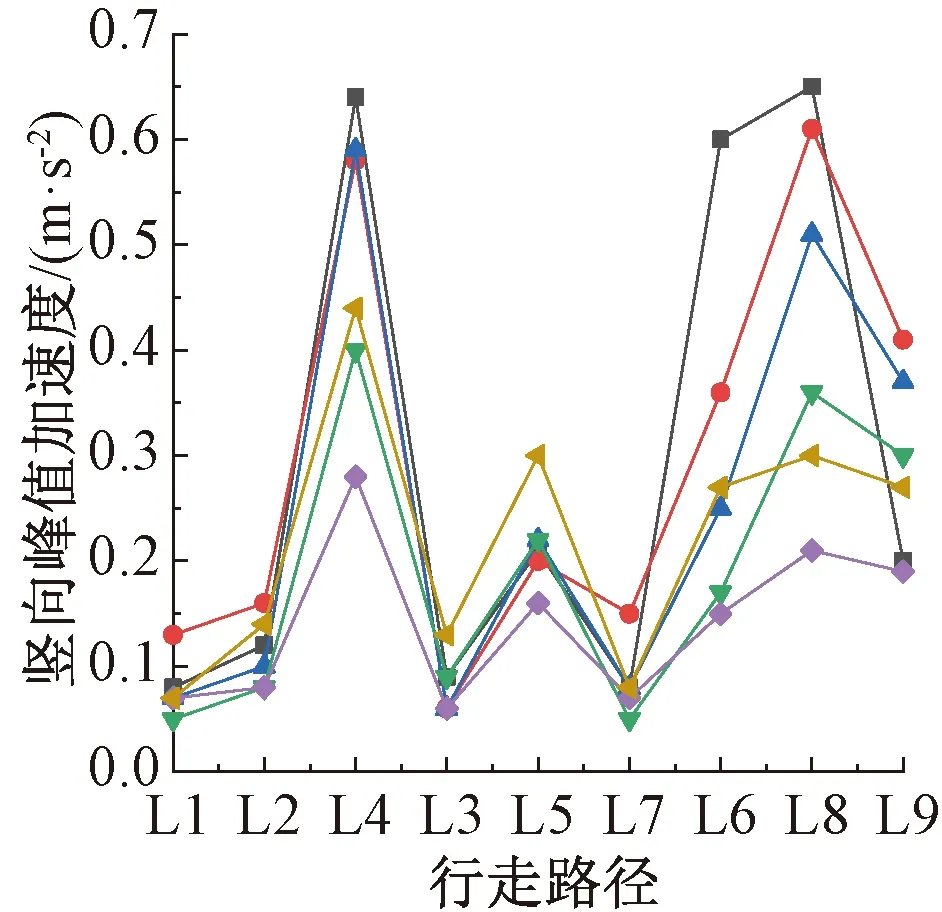
BQ1-1; BQ1-2; BQ1-3;BQ1-7; BQ2-6; BQ3-5。图5 不同行走路径下的峰值加速度Fig.5 Peak accelerations in different walking paths

3 不同参数对楼板舒适度影响

3.1 长宽比

为了研究长宽比对其振动特性的影响,从表2选取已建立的9个楼盖模型,共分为3组。第1组BQW-1由长宽比为6∶6、8∶6、 5∶3的BQ1-3、BQ1-5和BQ1-8组成,其钢板厚度均为10 mm,T型肋间距均为1.5 m;第2组BQW-2由长宽比分别为6∶6、8∶6、10∶6的BQ2-1、BQ2-2和BQ2-5组成,其钢板厚度均为6 mm,T型肋间距均为2.0 m;第3组BQW-3由长宽比分别为6∶6、8∶6、10∶6的BQ3-1、BQ3-2和BQ3-5组成,其钢板厚度均为8 mm,T型肋间距均为3.0 m;将3组模型进行模态分析和人行荷载的时程分析,得到的各楼盖的振动特性见表3,竖向峰值加速度曲线见图6所示。

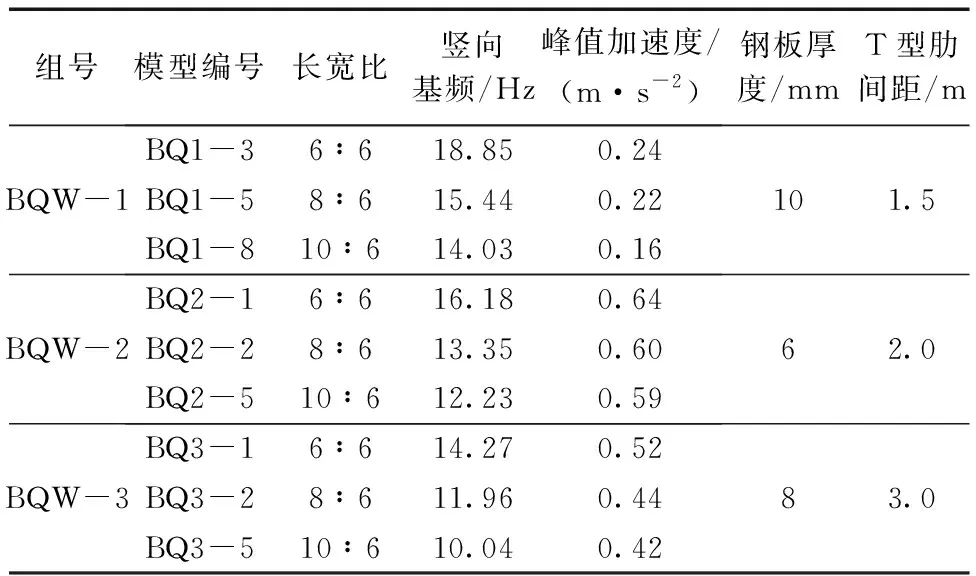
表3 不同长宽比下的楼盖振动特性Table 3 Floor vibration characteristics in different aspect ratios

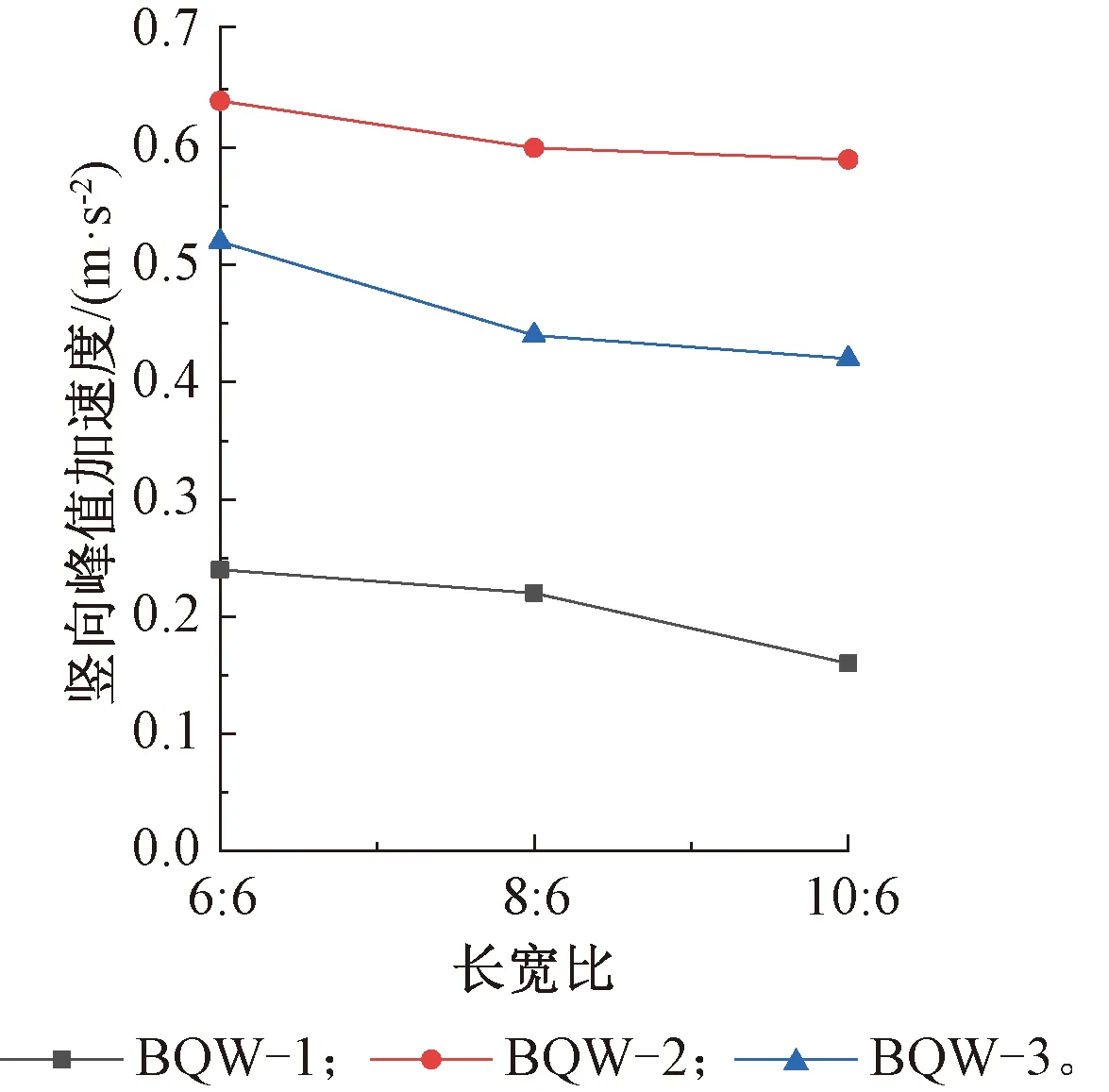
图6 长宽比对竖向峰值加速度的影响Fig.6 Influence of aspect ratios on vertical peak acceleration

比较BQW-1、BQW-2和BQW-3模型的竖向基频,由表3可知:三组模型的竖向基频随着长宽比的加大而显著降低,长宽比由6∶6增至10∶6时,竖向基频下降幅度分别为25.6%、24.4%和29.6%,通过竖向基频的下降幅度可以看出,三组模型的刚度都有所降低,且下降幅度逐渐减小,其原因是在钢板厚度和T型加劲肋间距不变的情况下,随着长宽比的增加,加劲肋的数量也在增加,导致楼盖整体质量增加,刚度下降变缓。由图6可知:三组模型的竖向峰值加速度都随着长宽比的增大而减小,下降幅度分别为33.3%,7.8%和19.2%。相比BQW-1组模型,BQW-2和BQW-3组模型的下降幅度较小,其原因在于BQW-1的质量和刚度较大,长宽比增大引起的刚度降低比其质量增加对竖向峰值加速度的影响更小。

3.2 钢板厚度

为了研究钢板厚度对其振动特性的影响,建立了9个楼盖模型,共分为3组。第1组BQW-4由钢板厚度为6,8,10 mm的BQ1-1、BQ1-2和BQ1-3组成,其长×宽均为6 m×6 m,T型肋间距均为1.5 m;第2组BQW-5由钢板厚度分别为6,8,10 mm的BQ2-2、BQ2-3和BQ2-4组成,其长×宽均为8 m×6 m,T型肋间距均为2.0 m;第3组BQW-6由钢板厚度分别为6,8,10 mm的BQ3-4、BQ3-5和BQ3-6组成,其长×宽均为10 m×6 m,T型肋间距均为3.0 m;将3组模型进行模态分析和人行荷载的时程分析,得到的各楼盖的振动特性见表4,加速度时程曲线如图7所示。

表4 不同钢板厚度下的楼盖振动特性Table 4 Floor vibration characteristics in different thicknesses of steel sheets

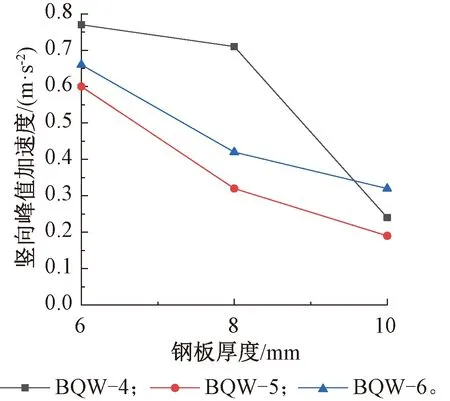
图7 钢板厚度对竖向峰值加速度的影响Fig.7 Influence of steel sheet thickness on vertical peak acceleration

比较BQW-4、BQW-5和BQW-6模型的竖向基频,由表4可得:三组模型的竖向基频随着钢板厚度的增大而增大,钢板厚度由6 m增至10 m时,竖向基频增大幅度分别为2.8%、1.8%和1.7%。通过竖向基频的增大幅度可以看出,三组模型的刚度增大并不明显,其原因是:在长宽比和T型加劲肋间距不变的情况下,随着钢板厚度的增加,加劲肋间距和数量未发生改变。由图7可知:三组模型的竖向峰值加速度都随着钢板厚度的增大而减小,下降幅度分别为68.8%,68.3%和51.5%。三组模型的竖向峰值加速度下降幅度较大,其主要原因在于:增大楼盖的钢板厚度,增大了楼盖整体自重,使得楼盖的惯性增大,抵抗振动的能力增强。相比于BQW-6,BQW-4于BQW-5的下降幅度更大,其原因在于BQW-6的T型加劲肋间距较大,楼盖整体刚度较弱,故其下降幅度更小。

3.3 加劲肋间距

为了研究楼盖T型加劲肋间距对其振动特性的影响,建立了9个楼盖模型,共分为3组。第1组BQW-7由T型加劲肋为1.5,2.0,3.0 m的BQ1-6、BQ2-5和BQ3-4组成,其钢板厚度均为6 mm,长×宽均为10 m×6 m;第2组BQW-8由加劲肋间距分别为1.5,2.0,3.0 m的BQ1-4、BQ2-3和BQ3-2组成,其钢板厚度均为8 mm,长×宽均为8 m×6 m;第3组BQW-9由T型加劲肋间距分别为1.5,2.0,3.0 m的BQ1-5、BQ2-4和BQ3-3组成,其钢板厚度均为10 mm,长×宽均为8 m×6 m;将3组模型进行模态分析和人行荷载的时程分析,得到的各楼盖的振动特性见表5,竖向峰值加速度曲线见图8所示。

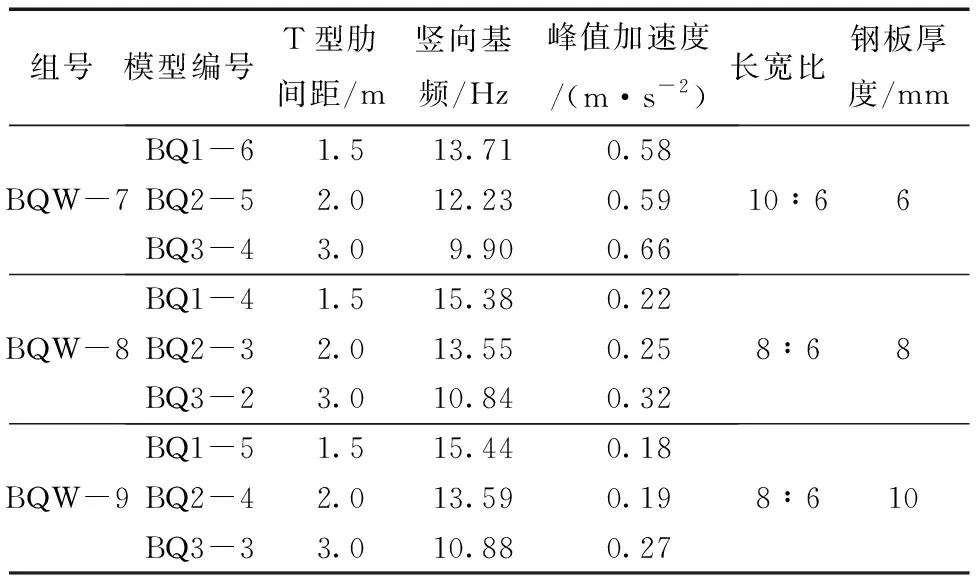
表5 不同T型加劲肋间距的楼盖振动特性Table 5 Vibration characteristics of floors with different T-stiffener spacing

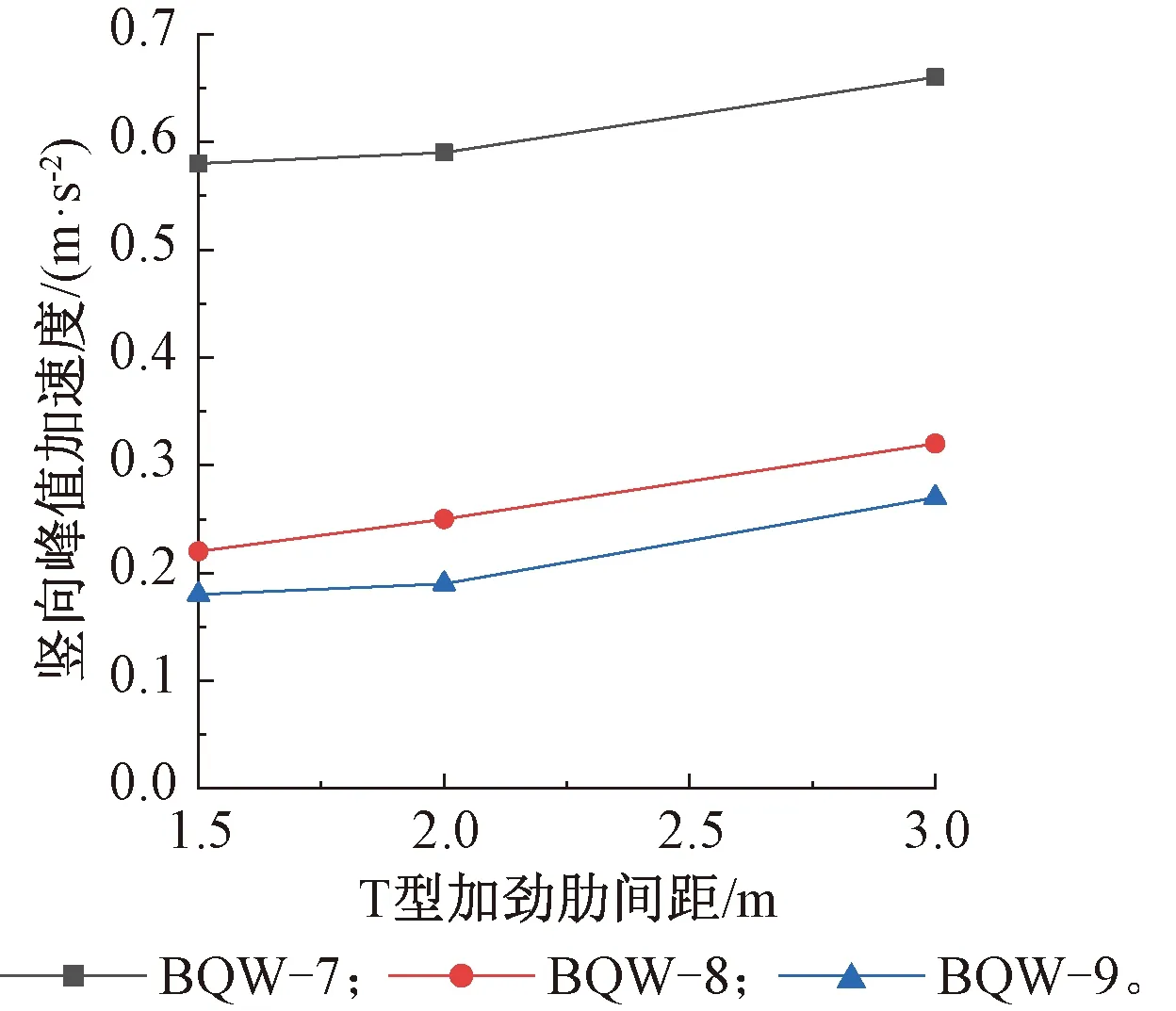
图8 T型加劲肋间距对竖向峰值加速度影响Fig.8 Influence of T-stiffener spacing on vertical peak acceleration

比较BQW-7、BQW-8和BQW-9模型的竖向基频,由表5可得:三组模型的竖向基频随着T型加劲肋间距的加大而显著降低,T型加劲肋间距由1.5 m增至3.0 m时,竖向基频下降幅度分别为27.8%、33.8%和29.5%。通过竖向基频的下降幅度可以看出:三组模型的刚度都有所降低,且下降幅度逐渐增大。其原因是在钢板厚度和长宽比不变的情况下,随着T型加劲肋间距的增加,加劲肋的数量在减少,导致楼盖整体质量降低且刚度急剧下降。由图8可知:三组模型的竖向峰值加速度都随着T型加劲肋间距的增大而增大,分别增加0.08,0.1～0.09 m/s2。其原因为增大T型加劲肋间距使楼盖划分的单元刚度降低,容易发生局部振动,导致局部峰值加速度增大。

4 基于TMD的舒适度优化设计

4.1 调谐质量阻尼器 TMD 的基本原理

调谐质量阻尼器作为一个子结构,主要由弹簧、阻尼器和质量块组成,一般支承或者悬挂在结构上。当主体结构在外部激励荷载作用下产生振动时,子结构由于动力响应产生振动,产生的惯性力反作用于主体结构,与主结构的振动进行协调,从而减少主结构的振动反应,提高主结构舒适度。根据Den Hartog研究的TMD系统的优化理论[10],以控制结构振动加速度为原则,此时TMD的最优频率比fopt和最优阻尼比ξopt的最优解析解如下:

(1a)

(1b)

其中μ=md/m

式中:μ为TMD系统质量与结构质量之比。

4.2 TMD 设置方案

4.2.1TMD布置方案

根据JGJ/T 441—2019《建筑楼盖结构振动舒适度技术标准》[11],当仅减小结构某一阶振型的振动时,可设置一种调频质量阻尼器,且宜安装于期望控制振型的峰值点附近。调频质量阻尼器周围应有安全净空及检修空间,以利于调频质量阻尼器的检查和维护。安装完成后,应使调频质量阻尼器处于平和位置,弹簧元件、阻尼元件应处于中位,吊索和橡胶支座不承受水平荷载或无水平变位。箱板装配式钢结构楼盖采用加劲钢板,吊顶后可为TMD提供良好的安装空间,故将TMD悬挂于峰值加速度控制点附近。以BQ2-2为例,人行荷载作用在x方向最不利路径L4下产生的加速度云如图9所示,作用在y方向最不利路径L8下产生的加速度云如图10所示,控制点位于L4与L8交汇处。在控制点处加入TMD,共有4个控制点。具体参数如表6所示,布置如图11所示。

表6 TMD布置Table 6 Arrangement of TMDs

图10 人行激励产生于最不利路径L8时的峰值加速度 m/s2Fig.10 Contours of peak acceleration excited by pedestrains on the most unfavorable path L8

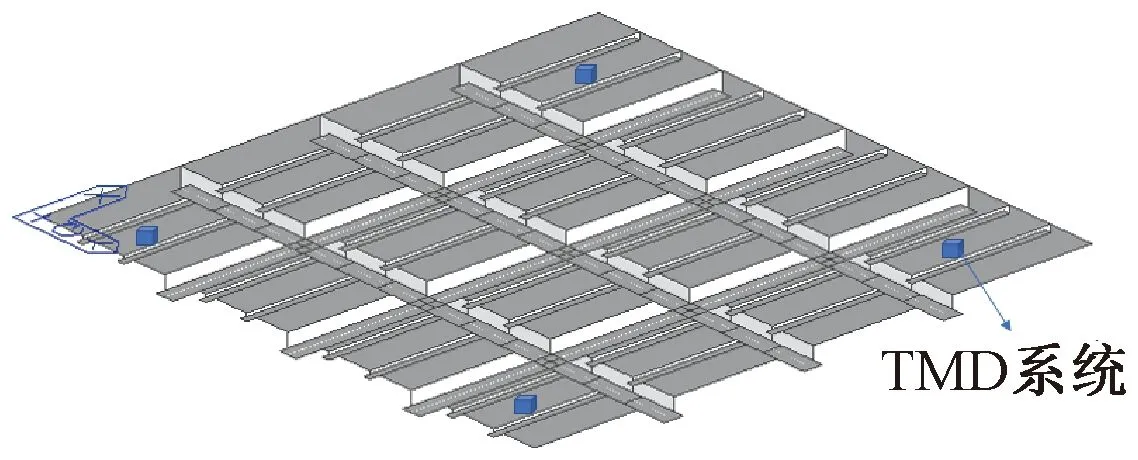
图11 6 m×6 m楼盖TMD布置Fig.11 Arrangements of TMDs beneath the 6 m×6 m floor

4.2.2TMD参数设置

根据 TMD 的最优频率和最优阻尼比算式,质量比μ取1%～5%,由楼盖的模态质量和固有频率得到阻尼器的有关参数,计算式如下:

k=m(2πf)2

(2a)

(2b)

式中:m为阻尼器质量;f为阻尼器频率;ξ为阻尼比;k为阻尼器刚度;c为阻尼系数。

从表2中选取模型1、2、10、13作为主结构。不同质量比TMD系统的相关参数如表7所示。

表7 TMD系统相关参数Table 7 Related parameters of TMD systems

由图12可知:当μ≤1%时各楼盖峰值加速度降低显著,随着质量比μ的增加,BQ1-1和BQ1-2的峰值加速度降幅减缓,其原因是随着质量比μ的增加,楼盖整体质量和刚度也在逐步增大,由局部振动慢慢转变成整体振动,最终也都能把峰值加速度控制在0.05 m/s2以下。而BQ2-2和BQ2-5在质量比μ>1%时出现峰值加速度上升,其原因是随着T型加劲肋间距的增大,单元刚度变弱,导致板块间的动力响应下降。当加劲肋间距过大,TMD控制振动范围有限,无法降低楼盖整体的竖向峰值加速度,只对局部振动有改善。因此,在箱板装配式钢结构楼盖设计过程中,应合理控制加劲肋间距,使TMD更有效发挥其作用。

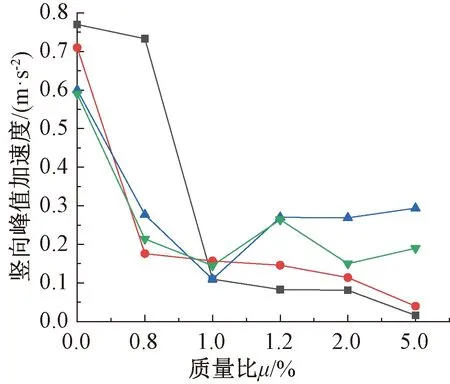
BQ1-1; BQ1-2; BQ2-2; BQ2-5。图12 不同质量比下的峰值加速度Fig.12 Peak accelerations in different mass ratios

5 结束语

通过对箱板装配式钢结构楼盖模型的计算分析,研究不同长宽比、钢板厚度、T型加劲肋间距及加入不同质量比的TMD对其舒适度性能的影响,可得到如下结论:

1)箱板装配式钢结构楼盖的长宽比会同时影响结构的刚度和质量,随着长宽比的增大,加劲肋数量增多,结构整体质量加大,整体刚度降低。

2)箱板装配式钢结构楼盖的钢板厚度主要影响结构质量,在不改变长宽比及加劲肋间距的情况下,整体刚度变化不大,随着板厚的增大,使得楼盖的惯性增大,抗振能力增强。

3)箱板装配式钢结构楼盖的加劲肋间距主要影响结构的刚度,相较于长宽比和钢板厚度,改变加劲肋间距对峰值加速度的影响较小。

4)人行荷载作用在T型肋上、L型肋上,T型肋与T型肋之间,L型肋与L型肋之间产生的加速度效应相差较大,应适当加强肋与肋之间薄弱部位的刚度以减小局部振颤带来的不舒适感。

5)对于箱板装配式钢结构楼盖的舒适度,设计过程中须要将加劲肋间距控制在合理范围内,使得加入调谐质量阻尼器(TMD)能更有效地增加参与振动的质量,从而提升楼盖舒适度,满足设计标准要求。